Рассмотрим формулу расчета цвета пикселя на экране при использовании, например, параллельного источника освещения:
LitColor = Ambient + Diffuse + SpecularИли, говоря более формально, сумму рассеянного, поглощенного и зеркального освещений. Каждый из них вычисляется так:
(цвет материала) * (цвет источника) * (коэффициент интенсивности)Долгое время в приложениях интерактивной графики коэффициент интенсивности рассеянного (Ambient) освещения был константным, но теперь мы можем рассчитать его в реальном времени. Я бы хотел рассказать об одном из таких методов — ambient occlusion, а точнее его оптимизации — screen space ambient occlusion. Поговорим сперва о методе ambient occlusion. Его суть в следующем — для каждой вершины сцены сформировать некий фактор, который будет определять степень «видимости» остальной сцены.
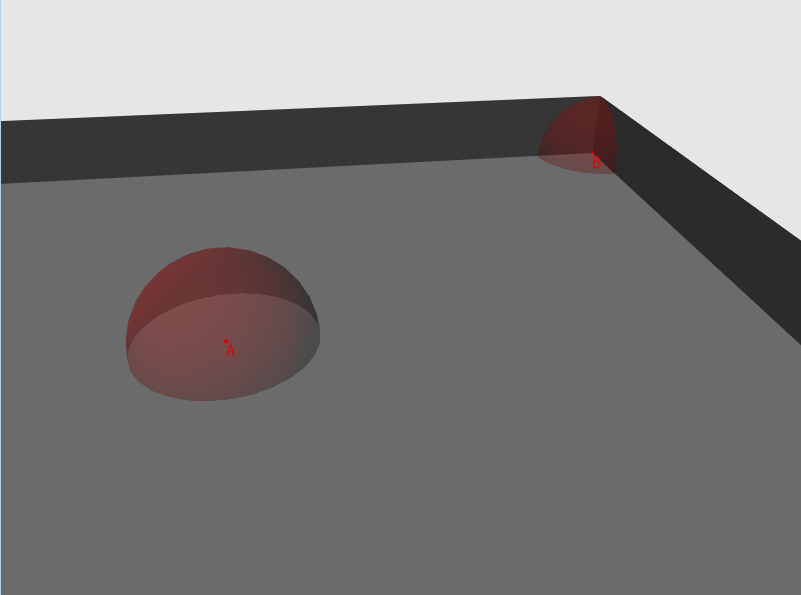
Рис.1 — рисунок с комнатой и двумя точками, «видимость» каждой точки изображена в виде сферы
Итак, для каждой вершины в случайных направлениях пустим лучи и найдем их пересечение с геометрией сцены. Далее посчитаем длину получившейся линии (если пересечение не было найдено, будем считать, что луч имеет некую максимальную для данной сцены длину) и сравним ее с пороговым значением. Если длина превышает пороговое значение — тогда луч проходит тест на «видимость».Количество пройденных тестов, деленное на количество пущенных лучей, и будет являться фактором «видимости».
Очевидно, что высокая вычислительная сложность алгоритма делает его неприменимым в реальном времени или для сцен с высокой динамикой объектов. Также эффективность метода сильно зависит от полигональной сложности сцены. Такой подход разумно применять, когда есть возможность заранее посчитать «видимость» и сохранить ее как часть данных вершин или в текстуре.
К счастью, ребята из CryTeck (по крайней мере, я слышал, что они были первыми) придумали способ, как рассчитать коэффициент в реальном времени. Он называется Screen Space Ambient Occlusion.
Алгоритм моей реализации следующий:
- 1. Берем NDC(normalized device coordinates) или текстурные координаты пикселя и преобразуем их в точку в пространстве камеры, используя при этом данные глубины;
- 2. Из этой точки в случайных направлениях пускаем N лучей;
- 3. Для каждого из N лучей:
- 3-а. умножаем (масштабируем) наш луч (вектор) на некое число (скаляр) и прибавляем его к точке из п.1;
- 3-b. Преобразуем полученную точку в пространство NDC, а затем в текстурные координаты;
- 3-c. Из текстуры получаем значение глубины для этой точки;
- 3-e. Если полученное значение меньше глубины точки, полученной в п.3-а, то имеет место «перекрытие» (см. рис.2). Надо учесть, чтобы эти значения принадлежали одной системе координат;
- 3-f. Получаем фактор «перекрытия» исходя из зависимости «Чем дальше точка из п.3-а от точки из п.1, тем потенциально меньше возможное перекрытие от этой точки». Аккумулируем его значение.
- 4. Получаем общий фактор «перекрытия», который равен общему суммарному перекрытию / N лучей. Tак как общий фактор принадлежит [0,1], а видимость обратно пропорциональна перекрытию, то она равняется 1 — перекрытие.
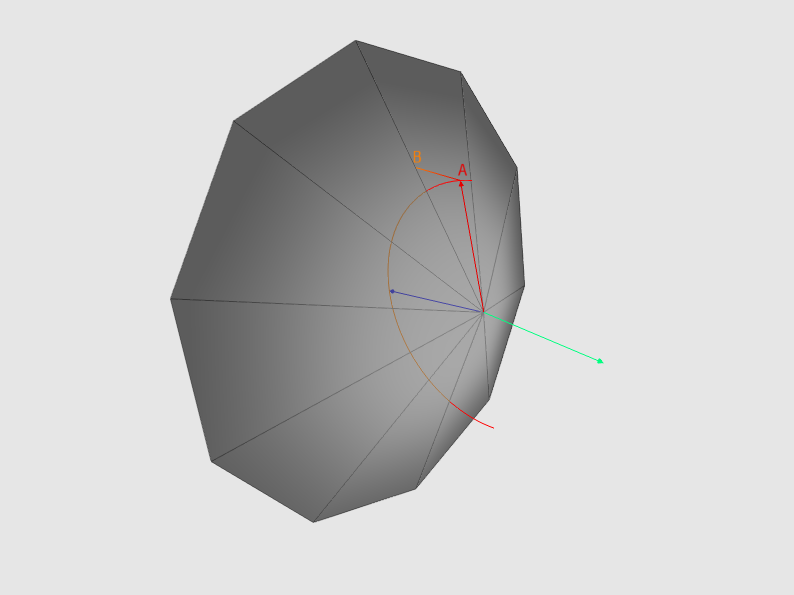
Рис.2 — синим цветом изображен вектор нормали, красным цветом изображен вектор, полученный в п.3-а. Светло зеленый вектор — направление оси Z. Если значение глубины в точке A больше, чем в точке B — это перекрытие. Для наглядности на рисунке используется ортогональная проекция (поэтому линия AB — прямая)
Применяя данный алгоритм в пиксельном шейдере, мы можем получить данные видимости, если запишем результат рендеринга в текстуру. Данные из этой текстуры можно в дельнейшем использовать при расчете освещенности сцены.
Итак, начнем.
1. Преобразования
Для того, чтобы из трехмерных координат получить координаты экранные, нам надо совершить ряд матричных преобразований.
В общем виде таких преобразований выделяют три:
- 1. Из локальных координат в мировые — перевести все объекты в общую систему координат
- 2. Из мировых координат в видовые координаты — ориентировать все объекты относительно «камеры»
- 3. Из видовых координат в координаты проекции — спроецировать вершины объектов на плоскость. Мы используем перспективную проекцию, которая подразумевает так называемое однородное деление (Homogeneous divide) — деление компонент x и у вершины на ее глубину — компоненту z.
Пункты 1 и 2 для нас не важны, поэтому перейдем сразу к п.3. Посмотрим на матрицу проекции:
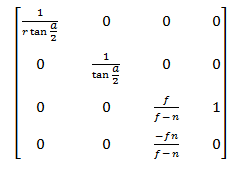
После умножения на эту матрицу координаты из пространства камеры переходят в пространство проекции
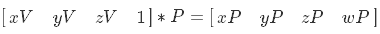
Далее следует однородное деление, в результате этого мы переходим в пространство NDC
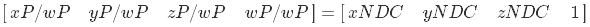
Теперь посмотрим, как осуществить обратное преобразование. Очевидно, сперва нам в шейдере нужны координаты пикселя. Я считаю, что удобнее всего использовать покрывающий всю экранную область квадрат в NDC пространстве с текстурными координатами от (0,0) до (1,1). Вот данные вершин:
struct ScreenQuadVertex
{
D3DXVECTOR3 pos = {0.0f, 0.0f, 0.0f};
D3DXVECTOR2 tc = {0.0f, 0.0f};
ScreenQuadVertex(){}
ScreenQuadVertex(const D3DXVECTOR3 &Pos, const D3DXVECTOR2 &Tc) : pos(Pos), tc(Tc){}
};
std::vector<ScreenQuadVertex> vertices = {
{{-1.0f, -1.0f, 0.0f}, {0.0f, 1.0f}},
{{-1.0f, 1.0f, 0.0f}, {0.0f, 0.0f}},
{{ 1.0f, 1.0f, 0.0f}, {1.0f, 0.0f}},
{{ 1.0f, -1.0f, 0.0f}, {1.0f, 1.0f}},
};
Также надо установить точечную интерполяцию данных текстуры, например D3D11_FILTER_MIN_MAG_MIP_POINT. Рисуя этот квадрат, мы можем либо «пробросить» данные вершины в пиксельный шейдер таким образом:
VOut output;
output.posN = float4(input.posN, 1.0f);
output.tex = input.tex;
output.eyeRayN = float4(output.posN.xy, 1.0f, 1.0f);Либо непосредственно в пиксельном шейдере преобразовать интерполированные текстурные координаты в NDC пространство вот так (подробнее о данном преобразовании см. в главе 3):
float4 posN;
posN.x = (Input.tex.x * 2.0f) - 1.0f;
posN.y = (Input.tex.y * -2.0f) + 1.0f;
Координаты пикселя в NDC пространстве у нас есть — теперь нужно перейти в видовое пространство. Исходя из свойства матриц:

Для наших целей надо иметь обратную матрицу проекции. Она выглядит так:
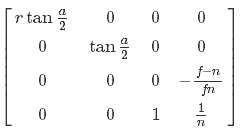
Но нам не достаточно просто умножить на нее двухмерную точку в NDC пространстве и совершить однородное деление — нам нужно также иметь данные о глубине точки, которую мы преобразовываем. Я хочу использовать глубину в пространстве вида — давайте проведем несколько алгебраических преобразований и узнаем, возможно ли это. Сперва выразим переход точки из видового в NDC пространство:
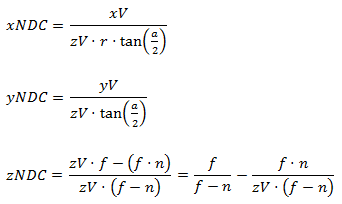
Теперь произведем умножение на обратную матрицу проекции:

Затем упростим X и Y и раскроем скобки в W:
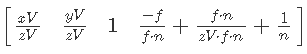
Далее продолжим упрощение в W:
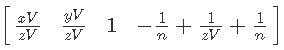
И последний штрих — сокращаем 1/n:

Выходит, что после умножения на обратную матрицу проекции нам нужно умножить результат на глубину в пространстве вида.Так и поступим. Сперва подготовим данные в пространстве NDC в вершинном шейдере:
output.eyeRayN = float4(output.posN.xy, 1.0f, 1.0f);Затем проделаем основную работу в пиксельном шейдере:
float4 normalDepthData = normalDepthTex.Sample(normalDepthSampler, input.tex);
float3 viewRay = mul(input.eyeRayN, invProj).xyz;
viewRay *= normalDepthData.w;Координаты в пространстве вида у нас есть. Идем дальше.
2. Трассировка лучей
2.1 Данные смещения
Итак, у нас есть координаты обрабатываемого пикселя в пространстве вида. Далее из точки с этими координатами нам надо пустить N лучей в случайных направлениях. К сожалению в API HLSL нет инструмента, с помощью которого мы могли бы получить случайное или псевдослучайное значение в процессе выполнения шейдера независимо от внешних данных (ну или я просто не знаю о существовании подобных технологий) — следовательно, мы подготовим такие данные заранее. Для того чтобы получить их в шейдере, проще всего использовать текстуру. Очевидно, что от формата пикселя зависит ее «вес» и предел значений данных. Для наших целей вполне подойдет формат DXGI_FORMAT_R8G8B8A8_UNORM. Теперь давайте разберемся с размером. Наверное, самый простой, наглядный и вместе с тем неоптимальный способ — создать текстуру с длиной и шириной равными разрешению экрана. В этом случае мы просто выбираем данные по значению текстурных координат квадрата, которые, напомню, находятся в пределах от (0,0) до (1,1). Но что будет, если мы выйдем за эти пределы? Тогда в игру вступают правила, указанные в перечислении D3D11_TEXTURE_ADDRESS_MODE. В данном случае нас интересует значение D3D11_TEXTURE_ADDRESS_MIRROR. Результат работы этого правила адресации показан на рис.3

Рис.3 — пример использования D3D11_TEXTURE_ADDRESS_MIRROR"
Если мы будем использовать данный подход, то для наших целей различия будут допустимы (см. рис.4).

Рис.4 — примитив с наложением текстуры 256х256 и с координатами от 0 до 1 и примитив с наложением текстуры 4х4 с координатами от 0 до 64 и адресацией D3D11_TEXTURE_ADDRESS_MIRROR
Теперь, наконец, давайте заполним текстуру данными. В шейдере мы будем формировать вектор случайного направления из компонентов R,G и B текселя, поэтому альфа канал мы не используем (его вы можете рассматривать как компонент W, который для векторов в однородном пространстве равен нулю). В итоге код примерно такой:
for(int y = 0; y < texHeight; y++){
for(int x = 0; x < texWidth; x++){
char* channels = reinterpret_cast<char*>(&data[y * texWidth + x]);
channels[0] = rand() % 255; //r
channels[1] = rand() % 255; //g
channels[2] = rand() % 255; //b
channels[3] = 0; //a
}
}Также хочу обратить внимание на то, что чем меньше размер текстуры, тем «чище» получится изображение (см. рис.5):
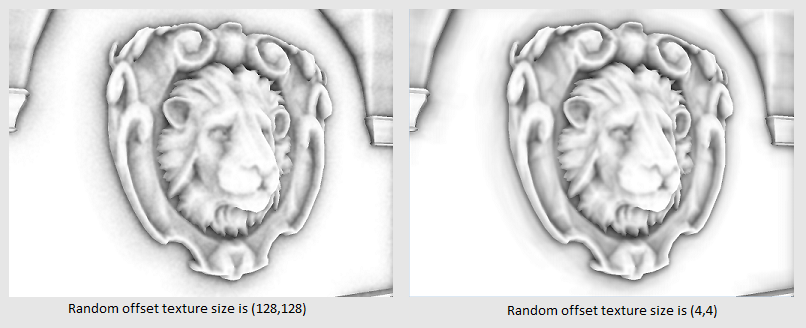
Рис.5 — демонстрация различия между текстурами смещений размеров 128х128 и 4х4
Ну вот, наша текстура готова — осталось только получить эти данные в шейдере. Но мы помним, что у нас есть текстурные координаты от 0 до 1, а нам надо использовать координаты от 0 до N, где N > 0. Решается эта задача очень просто на этапе подготовки шейдера — надо узнать, на сколько нужно умножить длину и на сколько нужно умножить ширину текстуры для того, чтобы она заняла весь экран. Предположим, что разрешение экрана 1024х768, а размер текстуры 2х4, тогда получим:
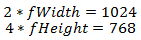
Теперь выразим коэффициенты:
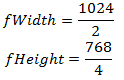
В итоге получаем такой код:
float2 rndTexFactor(fWidth, fHeight);
float3 rndData = tex.Sample(randomOffsetsSampler, input.tex * rndTexFactor).rgb;Возможно, в вашем случае более рационально будет хранить эти координаты выборки из текстуры смещения как данные вершин, тем самым получая уже готовое интерполированное значение.
Далее, так как мы выбрали формат DXGI_FORMAT_R8G8B8A8_UNORM, наше смещение находится в пространстве от 0 до 1. Перенесем его в пространство (-1, 1) (подробное описание преобразования см. в главе 3):
rndData = normalize(2.0f * rndData - 1.0f);Теперь у нас есть вектор смещения!
2.2 Ядро векторов смещения
Один вектор — это конечно хорошо, но нам ведь надо пустить N векторов. Мы можем получить некий фактор смещения текстурных координат в пределах от 0 до N и делать что-то подобное:
for(int i = 0; i < N; i++){
float3 rndData = tex.Sample(randomOffsetsSampler, input.tex * rndTexFactor + Offset * i).rgb;
rndData = normalize(2.0f * rndData - 1.0f);
/*...*/
}Этот вариант слишком ресурсоемкий. Давайте постараемся получить приемлемый результат используя лишь одну выборку из текстуры. Наша цель — добиться относительно разнородного распределения векторов как в пределах обрабатываемого пикселя, так и относительно соседних. Давайте возьмем N заранее подготовленных случайных векторов и каждый из них применим к нашему вектору смещения с определенной математической операцией. Этот набор назовем «Ядром векторов смещения». Уверяю вас, это проще чем я описал )
Подготовим наше ядро:
std::vector<D3DXVECTOR4> kernel(KernelSize);
int i = 0;
for(D3DXVECTOR4 &k : kernel){
k.x = Math::RandSNorm();
k.y = Math::RandSNorm();
k.z = Math::RandSNorm();
k.w = 0.0f;
D3DXVec4Normalize(&k, &k);
FLOAT factor = (float)i / KernelSize;
k *= Math::Lerp(0.1f, 0.9f, factor);
i++;
}
Значения для каждой компоненты генерируются от -1 до 1. Обратите внимание, что векторы не единичной длины. Это важно, так как в существенной степени влияет на итоговое изображение. На рис. 6 видно, что векторы не единичной длины при их проецировании образуют более сосредоточенное множество точек.

Рис.6 — проецирование векторов не единичной длины образует более сосредоточенное множество точек. Для большей наглядности использована ортогональная проекция
Ну вот, ядро готово — осталось использовать его в шейдере. В качестве математической операции я решил использовать «Отражение вектора». Этот инструмент весьма полезен и широко применяется — например если нам надо получить отраженный вектор к источнику света при расчете зеркального освещения или если нам нужно узнать, в какую сторону полетит мяч, отскочивший от стены. Формула расчета отраженного вектора выглядит так:

где v — вектор, который мы собираемся отразить, n — нормаль к поверхности, относительно которой мы будем отражать вектор (см. рис.7)

Рис.7 — визуализация формулы отраженного вектора
Последнее, что нам нужно сделать с вектором — добиться того, чтобы он находился в пределах полусферы, ориентированной нормалью. Для этого мы поменяем его направление, если его скаларное произведение с нормалью меньше нуля. В итоге у нас получился следующий код:
//float3 kernel[N] - ядро векторов смещения
//normalV - нормаль пикселя в пространстве вида
float3 rndData = tex.Sample(randomOffsetsSampler, input.tex * rndTexFactor + Offset * i).rgb;
rndData = normalize(2.0f * rndData - 1.0f);
for(int i = 0; i < N; i++){
float3 samplingRayL = reflect(kernel[N], rndData);
samplingRayL *= sign(dot(samplingRayL, normalV));
/*...*/
}Обратите внимание, что мы не нормализуем результат операции reflect().
3. От луча к точке на экране
Давайте оглянемся назад и посмотрим, что у нас получилось. Итак:
- Используя данные глубины, мы получили координаты пикселя в пространстве вида
- Мы получили N лучей, случайно распределенных относительно друг друга
Теперь у нас есть все, что нужно для того, чтобы наконец узнать, что вокруг нас. Продолжим. Умножаем наш вектор на некий скаляр occlusionRadius и прибавляем его к точке нашего пикселя в пространстве вида. Разумно позволить художнику регулировать значение occlusionRadius.
//viewRay - координаты пикселя в пространстве вида
float3 samplingPosV = viewRay + (samplingRayL * occlusionRadius);
Говоря формально, в пространстве вида мы получили точку samplingPosV, которая расположена на некотором расстоянии от нашего пикселя по направлению samplingRayL. Далее спроецируем полученную точку на экран, не забывая при этом произвести «однородное деление», чтобы учесть глубину:
float4 samplingPosH = mul(float4(samplingPosV, 1.0f), proj);
float2 samplingRayN = samplingRayH.xy / samplingRayH.w;Мы в пространстве NDC. Теперь нам надо перейти в пространство координат текстуры. Для этого преобразуем нашу точку из области значений от -1 до 1 в область от 0 до 1. Обратите внимание, что ось Y направлена в противоположную сторону. (см. рис.8)

Рис.8 — демонстрация координатных осей для NDC и пространства координат текстуры
Давайте сперва преобразуем координату Х. В общем виде одномерные преобразования такого рода можно выполнять следующим образом — сперва отнимаем минимальное значение диапазона, затем делим на ширину диапазона (максимальное значение минус минимальное), затем полученный коэффициент умножаем на ширину диапазона нового пространства и к полученному результату прибавляем минимальное значение нового пространства. Уверяю вас, это проще сделать, чем сказать. Для нашего случая предположим, что Nx — координата X в NDC пространстве, Tx — координата X в пространстве координат текстуры. Получается следующее:

Так как координата Y в NDС пространстве направлена в противоположную сторону, действовать нужно несколько иначе. Мы не можем просто взять значение с противоположным знаком, так как мы тут же выйдем за допустимые границы. Хмм… Представьте точку в правом нижнем углу экрана — в пространстве NDC ее координаты будут (1, -1), а в пространстве координат текстуры — (1, 1). Теперь представьте точку в левом верхнем углу — у нее в NDC пространстве координаты будут (-1, 1), а в пространстве координат текстуры — (0, 0). Вырисовывается следующая закономерность — для граничных областей Y принимает максимальное значение в одной системе координат и минимальное в другой и наоборот. Следовательно, когда мы получим наш коэффициент — мы отнимем его от единицы.

Мы можем решить эту задачу другим способом. Решение представлено в приложении 1.
В итоге в шейдере мы получаем следующий код:
float2 samplingTc;
samplingTc.x = 0.5f * samplingRayN.x + 0.5f;
samplingTc.y = -0.5f * samplingRayN.y + 0.5f;Добавлю, что можно совместить преобразование к текстурным координатом и проецирование в одной матрице следующим образом (Р — матрица проекции):

4. Работа с данными глубины
Осталось совсем немного! Скорей, скорей! По полученным в предыдущем пункте координатам делаем выборку из текстуры с данными.
float sampledDepth = normalDepthTex.Sample(normalDepthSampler, samplingTc).w;В компоненте w хранятся данные глубины — берем их и! И… И что же нам с ними делать!? Давайте подумаем. Мы находимся в пространстве вида — ось Z совпадает с направлением камеры. Следовательно, чем меньше полученная глубина, тем ближе к нам находится объект. Напомню, что мы спроецировали точку, которая расположена в некотором отдалении от нашего пикселя в пространстве вида. В текстуре хранится глубина также в пространстве вида. Что мы узнаем, если сравним глубину из текстуры с глубиной нашей точки? Если значение глубины из текстуры меньше, чем глубина точки — тогда что-то расположено ближе к камере и наша точка не будет видна.Соответственно наша точка видна, если она ближе к камере, чем это «что-то». Кстати, примерно также работает ShadowMapping. Это как если вам на машине надо совершить сложный маневр, а вы не видите, что происходит снизу, и вы просите друга отрегулировать ваше движение. А он пьян и посчитал, что сообщать вам данные, противоположные ожидаемым вами будет весьма забавно… Но это не наш случай )
Так вот, чем меньше точек из N множества видно камере, тем меньше рассеянного освещения получает наш пиксель. Можно рассмотреть ситуацию несколько иначе — давайте представим, что мы смотрим из нашего пикселя в направлении его нормали (потому что лучи распределяются в пределах полусферы, ориентированной нормалью). Чем меньше точек из N множества видно камере, тем меньшее количество объектов сцены мы можем увидеть из нашего пикселя (потому что все больше «геометрии» объектов сцены перекрывает нам обзор) — следовательно тем меньше доступа к рассеянному свету сцены (Черт! Папа заставил мой плакат «Iron maiden» своими лыжами! Пикачу! Я призываю тебя!!)
Также надо учесть, что некий объект сцены, глубину которого мы получили, может находиться настолько далеко, что никак не повлияет на доступ к рассеянному свету к точке пикселя (см. рис. 9)

Рис.9 — Точка q хоть и ближе к камере, но расположен слишком далеко от точки пикселя P и не может влиять на его освещенность
Я предлагаю не просто прибавлять 1, а некий коэффициент, зависимый от расстояния:
float distanceFactor = (1.0f - saturate(abs(viewRay.z - sampledDepth) / occlusionRadius)) * harshness;Обратите внимание, что мы формируем коэффициент расстояния исходя из глубины точки пикселя, а не той точки, которую мы проецировали — ее мы использовали, чтобы понять, есть ли что-то перед нами, а теперь нам надо понять, насколько далеко это «что-то» от нас находится. Также я добавил возможность регулировать интенсивность через параметр harshness.
В общем, это основная часть алгоритма, так сказать heart of it all. Давайте посмотрим на весь цикл работы с векторами смещения:
//viewRay - координаты пикселя в пространстве вида
//normalV - нормаль пикселя в пространстве вида
//float3 kernel[N] - ядро векторов смещения
//offset - случайный вектор смещения, полученный из текстуры
float totalOcclusion = 0.0f;
[unroll]
for(int i = 0; i < 16; i++){
float3 samplingRayL = reflect(kernel[i].xyz, offset);
samplingRayL *= sign(dot(samplingRayL, normalV));
float3 samplingPosV = viewRay + (samplingRayL * occlusionRadius);
float4 samplingPosH = mul(float4(samplingPosV, 1.0f), proj);
samplingPosH.xy /= samplingPosH.w;
float2 samplingTc;
samplingTc.x = 0.5f * samplingPosH.x + 0.5f;
samplingTc.y = -0.5f * samplingPosH.y + 0.5f;
float sampledDepth = normalDepthTex.Sample(normalDepthSampler, samplingTc).w;
if(sampledDepth < samplingPosV.z){
float distanceFactor = (1.0f - saturate(abs(viewRay.z - sampledDepth) / occlusionRadius));
totalOcclusion += distanceFactor * harshness;
}
}Давайте посмотрим на результат!

«Эй! Что это за фигня! И где здесь FarCry?!»- спросите вы. «Спокойно!» — отвечу я вам. «Чип и Дейл спешат на помощь!» Ой, это не из той статьи — «Blur спешит на помощь!»
5. Используем Blur
5.1 самый простой вариант
Эффект размытия, или Blur — очень полезный инструмент, который применяется во многих областях графики. Я бы сравнил его с изолентой (синей! Это важно) — с ее помощью можно что-то исправить или улучшить, но едва ли удастся починить телефон, который упал на кафель с высоты шкафа (хотя инструкции вроде «Обмотай изоляцией, и все нормально будет» встречал не раз).
Суть эффекта проста: для каждого текселя получить среднее арифметическое цветов его соседей
Итак, предположим, что у нас есть тексель с координатами P — давайте посчитаем среднее арифметическое цветов его соседей в области R (AreaWidth на AreaHeight пикселей). Примерно так (я намеренно не произвожу проверки на выход за границы массива. Об этом ниже):
D3DXCOLOR **imgData = ...; //Данные изображения
D3DXCOLOR avgColor(0.0f, 0.0f, 0.0f, 0.0f);
for(INT x = P.x - AreaWidth / 2; x <= P.x - AreaWidth / 2; x++)
for(INT y = P.y - AreaHeight / 2; y <= P.y - AreaHeight / 2; y++)
avgColor += imgData[x][y];
avgColor /= AreaWidth * AreaHeight;5.2 фильтр Гаусса
Теперь давайте сделаем вот что — цвет каждого соседа будем умножать на значение из матрицы, размерность которой равна AreaWidth на AreaHeight. Также обеспечим, чтобы сумма всех элементов матрицы была равна 1 — это избавит нас от необходимости деления на размер области, потому как теперь это будет уже частный случай среднего арифметического взвешенного. Такую матрицу формально принято называть «Матрицей свёртки», также ее называют «Ядром», а ее элементы — «весами». Зачем это нужно? Так у нас больше возможностей — контролируя значение весов, мы можем добиться, например, эффекта пульсации или постепенного размытия. Также существует целое семейство фильтров, основанных на матрице свёртки — фильтр улучшения четкости, медианный фильтр, фильтры эрозия и наращивание.
Самым распространенным фильтром для размытия является фильтр Гаусса. Его важным свойством является линейная сепарабельность — Это позволяет нам сперва размыть входное изображение по строкам, затем размытое по строкам изображение размыть по столбцам, выполняя один цикл со значениями одномерного фильтра, формула которого имеет вид:

где x — целое число от -AreaWidth/2 до AreaWidth/2, q — так называемое «Стандартное отклонение распределения Гаусса» (the standard deviation of the Gaussian distribution)
Я реализовал функцию, которая формирует матрицу фильтра:
typedef std::vector<float> KernelStorage;
KernelStorage GetGaussianKernel(INT Radius, FLOAT Deviation)
{
float a = (Deviation == -1) ? Radius * Radius : Deviation * Deviation;
float f = 1.0f / (sqrtf(2.0f * D3DX_PI * a));
float g = 2.0f * a;
KernelStorage outData(Radius * 2 + 1);
for(INT x = -Radius; x <= Radius; x++)
outData[x + Radius] = f * expf(-(x * x) / a);
float summ = std::accumulate(outData.begin(), outData.end(), 0.0f);
for(float &w : outData)
w /= summ;
return outData;
}Я использую радиус 5, а отклонение — 5 в квадрате.
5.3 Шейдер и все, что с ним связано
Мы будем использовать две текстуры — одна с исходными данными, другая для хранения промежуточного результата. Создадим обе текстуры с размерами, соответствующими разрешению экрана и форматом пикселя DXGI_FORMAT_R32G32B32A32_FLOAT. Можно конечно, не сильно потеряв в качестве, уменьшить размер текстур, но в данном случае я решил этого не делать. Работать с текстурами будем по следущей схеме:
//рисуем в временную текстуру
{
//размываем исходные данные по вертикали
}
//рисуем в текстуру с исходными данными
{
//размываем по вертикали данные из временной текстуры
}Как и ранее, работать будем с квадратом в NDC пространстве, который занимает всю экранную область, с текстурными координатами от 0 до 1. Теперь самое время подумать над тем, как обрабатывать выход за границы текстуры.
Реализовывать проверки непосредственно в коде шейдера слишком ресурсоемко. Давайте посмотрим, какие у нас есть варианты, если мы все же выйдем за границы области.Как я говорил ранее, в этом случае в игру вступают правила, указанные в перечислении D3D11_TEXTURE_ADDRESS_MODE. Нам подойдет правило D3D11_TEXTURE_ADDRESS_CLAMP. Происходит следующее — каждая из координат ограничивается диапазоном [0, 1]. То есть, если мы делаем выборку с координатами (1.1, 0), — мы получим данные текселя с координатами (1, 0), если выбирать для координат (-0.1, 0), — получим данные в (0, 0). То же самое для У (см. рис. 12).

Рис.12 демонстрация D3D11_TEXTURE_ADDRESS_CLAMP применительно к размеру фильтра
Последнее, что нам осталось узнать — на сколько нам надо продвинуться, чтобы переместиться на один пиксель в пространстве координат текстуры. Эта задача решается просто — допустим, что разрешение экрана 1024 на 768 пикселей, тогда, например, центр экрана в пространстве от 0 до 1 будет (512 / 1024, 384 / 768) = (0.5 0.5), а точка, расположенная на один пиксель от левого верхнего угла — (1 / 1024, 1 / 768). Также можно выразить решение этой задачи в виде уравнения. Пусть (Sx,Sy) — наша начальная позиция, (Ex,Ey) — конечная позиция, тогда ответ на вопрос «На какую часть экрана нам надо продвинуться, чтобы переместиться из S в E?» будет выглядеть так:

Предположим, что мы хотим переместиться из левого верхнего угла экрана на один пиксель, тогда уравнение будет выглядеть так:

Выражаем для F и получаем:

Теперь, пожалуй, можно привести код пиксельного шейдера:
cbuffer Data : register(b0)
{
float4 weights[11];
float2 texFactors;
float2 padding;
};
cbuffer Data2 : register(b1)
{
int isVertical;
float3 padding2;
};
struct PIn
{
float4 posH : SV_POSITION;
float2 tex : TEXCOORD0;
};
Texture2D colorTex :register(t0);
SamplerState colorSampler :register(s0);
float4 ProcessPixel(PIn input) : SV_Target
{
float2 texOffset = (isVertical) ? float2(texFactors.x, 0.0f) : float2(0.0f, texFactors.y);
int halfSize = 5;
float4 avgColor = 0;
for(int i = -halfSize; i <= halfSize; ++i){
float2 texCoord = input.tex + texOffset * i;
avgColor += colorTex.Sample(colorSampler, texCoord) * weights[i + halfSize].x;
}
return avgColor;
}Вершинный шейдер здесь приводить не стал, потому что там ничего особенного не происходит — просто «пробрасываем» данные дальше. Давайте посмотрим, что у нас получилось:

Рис.13 демонстрация размытия без учета граней
Неплохо, но теперь надо решить проблему размытых граней. В нашем случае сделать это это проще, чем может показаться на первый взгляд — ведь все необходимые данные у нас уже есть! Если мы находимся в экранном пространстве, то нам достаточно отследить скачкообразные изменения в данных нормали и глубины. Если скалярное произведение нормалей или абсолютное значение разницы глубин соседнего и обрабатываемого пикселя больше или меньше определенных значений, то мы полагаем, что обрабатываемый пиксель принадлежит линии грани. Я написал небольшой шейдер, который выделяет грани желтым цветом. Принцип работы тот же, как и для размытия — проходим сперва по вертикали, затем по горизонтали. Сравнивать будем двух соседей либо слева и справа, либо сверху и снизу — в зависимости от направления. Получилось примерно так:
bool CheckNeib(float2 Tc, float DepthV, float3 NormalV)
{
float4 normalDepth = normalDepthTex.Sample(normalDepthSampler, Tc);
float neibDepthV = normalDepth.w;
float3 neibNormalV = normalize(normalDepth.xyz);
return dot(neibNormalV, NormalV) < 0.8f || abs(neibDepthV - DepthV) > 0.2f;
}
float4 ProcessPixel(PIn input) : SV_Target
{
float2 texOffset = (isVertical) ? float2(0.0f, texFactors.y) : float2(texFactors.x, 0.0f);
float4 normalDepth = normalDepthTex.Sample(normalDepthSampler, input.tex);
float depthV = normalDepth.w;
float3 normalV = normalize(normalDepth.xyz);
bool onEdge = CheckNeib(input.tex + texOffset, depthV, normalV) || CheckNeib(input.tex - texOffset, depthV, normalV);
return onEdge ? float4(1.0f, 1.0f, 0.0f, 1.0f).rgba : colorTex.Sample(colorSampler, input.tex) ;
}
Рис.14 демонстрация выделения граней
Как нам это использовать при размытии? Очень просто! Мы не будем учитывать цвет тех соседей, которые очень далеко либо значительно отличаются направлениями нормалей от пикселя, цвет которого мы считаем. Только теперь надо делить результат на сумму обработанных весов. Вот код:
float4 ProcessPixel(PIn input) : SV_Target
{
float2 texOffset = (isVertical) ? float2(0.0f, texFactors.y) : float2(texFactors.x, 0.0f);
float4 normalDepth = normalDepthTex.SampleLevel(normalDepthSampler, input.tex, 0);
float depthV = normalDepth.w;
float3 normalV = normalize(normalDepth.xyz);
int halfSize = 5;
float totalWeight = 0.0f;
float4 totalColor = 0.0f;
[unroll]
for(int i = -halfSize; i <= halfSize; ++i){
float2 texCoord = input.tex + texOffset * i;
float4 normalDepth2 = normalDepthTex.SampleLevel(normalDepthSampler, texCoord, 0);
float neibDepthV = normalDepth2.w;
float3 neibNormalV = normalize(normalDepth2.xyz);
if(dot(neibNormalV, normalV) < 0.8f || abs(neibDepthV - depthV) > 0.2f)
continue;
float weight = weights[halfSize + i].x;
totalWeight += weight;
totalColor += colorTex.Sample(colorSampler, texCoord) * weight;
}
return totalColor / totalWeight;
}В итоге получилось так:

6. Неожиданные изменения
Когда я заканчивал работу над этой статьей, в результате очередного тестирования обнаружил, что результат перекрытия нестабилен относительно направления камеры. Для того, чтобы это исправить, нам нужно перевести координаты обрабатываемого пикселя и точки из п.3 из пространства вида в мировое. В моем случае проблема усугубляется тем, что все важные данные я храню в пространстве вида, поэтому в цикле по всем лучам нам нужно преобразовать либо глубину точки в пространства вида, либо глубину из текструры в мировое пространство. Также нам нужно не забыть перевести нормаль в мировое пространство, но не столь критично, так как не зависит от цикла.
7. Заключение
Хочу поблагодарить читателя за внимание к моей статье и надеюсь, что информация, в ней изложенная, была ему доступна, интересна и полезна. Отдельно хочу поблагодарить Леонида ForhaxeD за его статью — я многое от нее взял и постарался улучшить.
Исходный код примера можно скачать по адресу github.com/AlexWIN32/SSAODemo. Предложения и замечания касательно работы примера в целом или отдельных его подсистем можете присылать мне по почте или оставлять в качестве комментариев. Желаю вам успеха!

где MinVal — минимальное значение диапазона, Range — ширина диапазона, Factor — коэффициент, который принадлежит множеству значений от 0 до 1. Так как мы переходим из NDC пространства, я полагаю, что точка с коэффициентами, равными единице, будет расположена в левом верхнем углу экрана. Для NDC координат имеем

Для текстурных координат:

Далее выражаем коэффициенты:

Для текстурных координат:

Далее, полагая, что результат уравнений с одинаковыми коэффициентами представляет из себя одну и ту же точку на экране, формируем следующее равенство:

Далее выражаем его через наши уравнения:


В итоге получаем:

Комментарии (14)

Overlordff
19.09.2016 22:43+2Извините, пожалуйста, за нескромный вопрос. Мне очень интересно, где Вы всему этому научились? В вузе, непосредственно на «предприятии» или сами? Если сами, то что использовали для обучения? Подскажите, пожалуйста, какие темы копать кроме, разумеется, векторной алгебры. Просто я сейчас на первом курсе и надо уже расставить более-менее приоритеты, начать углубление в те, области, которые потом позволят заниматься подобным «волшебством». Заранее спасибо за ответ!

lgorSL
20.09.2016 00:09Я не автор статьи, но подобный вопрос у меня возникал несколько лет назад.
Из институтских курсов реально необходима линейная алгебра. Без неё никак.
Ещё время от времени появляются некоторые отсылки к матану и физике (эффекты преломления и отражения, сохранение количества света, сферические функции, преобразование Фурье, кватернионы) — лучше в них самому разбираться. В компьютерной графике они довольно спецефически применяются, в общих курсах такого может и не быть.
Главный совет — учиться читать на техническом английском, на нём документация и есть хорошие материалы. (На русском может быть устаревшая информация, если вообще будет)
Я начинал с F. Dunn, I. Parberry — "3D Math Primer for Graphics and Game Development". Там есть описание алгоритмов и примеры кода на с++. Начинается с самых азов типа векторов и систем координат — мне было знакомо, но зато помогло привыкнуть к английским наименованиям.

AlexWIN32
20.09.2016 00:14+1Вот уж такого вопроса не ожидал)) Учусь потихоньку сам. Из книг могу порекомендовать
Mathematics for 3D Game Programming and Computer Graphics, Third Edition 3rd Edition by Eric Lengyel
https://www.amazon.com/dp/1435458869/ref=pd_lpo_sbs_dp_ss_1?pf_rd_p=1944687722&pf_rd_s=lpo-top-stripe-1&pf_rd_t=201&pf_rd_i=159200038X&pf_rd_m=ATVPDKIKX0DER&pf_rd_r=7039KSJ1H4BNPTQ2X7WX
Насколько я понимаю, этот труд обрел уже статус классического
Introduction to 3D Game Programming with DirectX 11 by Frank Luna
Отличная книга, весьма подробно описывающая как многие современные техники рендеринга, так и основы. Рекомендую.
(Кстати, при написании этой статьи во многом опирался на эту книгу)
https://www.amazon.com/Introduction-3D-Game-Programming-DirectX/dp/1936420228
HLSL Development Cookbook by Doron Feinstein
Весьма доступно раскрываются методы реализации более продвинутых приемов рендеринга. Cascaded shadow mapping, Dynamic sun shafts и многое другое ждет вас на страницах этой книги
Темы кроме алгебры — английский(если у вас с ним конечно проблемы как у меня)) ). А если ближе к предметной области — то рекомендую копать все. Я вот в определенный момент понял, что не понимаю то, о чем пишут в тех же GPU Gems или ShaderX и начал слушать алгебру с самого начала на khanacademy. Я болшьше, к сожалению, не могу вам ничего посоветовать, потому как сам еще только учусь. Я желаю вам успехов в учебе и в работе!
AlexWIN32
20.09.2016 00:25+2Как же я мог забыть!!!
Андре Ламот. Программирование трехмерных игр для Windows
(https://www.ozon.ru/context/detail/id/1692806/)
Это просто вещь!!! Автор рассказывает, как написать свой конвеер рендеринга с нуля. Это определенно ваш выбор, если вы хотите понять, «как», «что» и «почему». Кто-то может сказать, что книга устарела — мол, там нет суперэффектов и шейдеров — на что я отвечу, что знания, в ней изложенные, настолько фундаментальны, что вне времени


lgorSL
Для использования фильтра Гаусса (и для более простого варианта с суммированием в квадрате) можно применить фильтр по вертикали и потом по горизонтали (или наоборот) — сложность вместо O(width*height) изменится на O(width+height).
С гауссом фишка в том, что вес пропорционален exp(-adx^2-bdy^2) = exp(-adx^2) exp(-b*dy^2), и он распадается на две независимые составляющие по каждой координате.
lgorSL
Сорри, не заметил, что Вы это тоже написали. Слово "матрица" и пример с суммированием цветов в квадрате ввели в заблуждение.
AlexWIN32
Ничего) Спасибо за внимание к статье!