Задача решалась в двумерном случае простой явной разностной схемой. Неявные схемы я не люблю, и они требуют много памяти. Расчет с нормальной точностью требует сеток малого шага, по сравнению с более простыми методами требуется очень много времени. Поэтому максимальный упор был сделан на производительность.
Представлена реализация алгоритма на Java и C++.

Предисловие
Около шести лет основным моим языком для расчетов и мелочей был Matlab. Причина — простота написания и визуализации результата. А так как перешел я с Borland C++ 3.1, то прогресс возможностей был очевиден. (В Python я никогда не шарил, а в С++ тогда слабо).
FDTD нужен был мне для расчетов как надежный и достоверный метод. Начал изучать вопрос в 2010–11 годах. Имеющиеся пакеты или было непонятно, как использовать, или не умели то, что мне нужно. Решил написать свою программу для четкого контроля над всем. Прочитав классическую статью «Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media», написал трехмерный случай, но потом упростил его до двумерного. Почему 3D — это сложно, объясню потом.
Потом максимально оптимизировал и упрощал код Matlab. После всех улучшений получилось, что сетка 2000х2000 проходится за 107 минут. На i5-3.8 ГГц. Тогда такой скорости хватало. Из полезного было то, что в Матлабе сразу шел расчет комплексных полей, и легко было показывать картинки распространения. Также все считалось на даблах, потому что на скорость Матлаба практически не влияло. Да, стандартный мой расчет — один проход света по фотонному кристаллу.
Проблемы было две. Понадобилось с высокой точностью вычислять спектры, а для этого использовать большую ширину сетки. А физическое увеличение области по обеим координатам в 2 раза увеличивает время расчета в 8 раз (размер кристалла*время прохода).
Matlab я продолжал использовать, но стал Java-программистом. И, сравнивая производительность разных алгоритмов, начал что-то подозревать. К примеру, сортировка пузырьком — только циклы, массивы и сравнения — в Матлабе работает в 6 раз медленнее, чем в С++ или Java. И этого для него еще хорошо. Пятимерный цикл для гипотезы Эйлера в Матлабе раз в 400 дольше.
Вначале принялся писать FDTD на C++. Там был встроенный std::complex. Но тогда я забросил эту идею. (В Матлабе не такие скобочки, копипаст не работал, пришлось потратить каплю времени). Сейчас проверил C++ — комплексная математика дает потери скорости в 5 раз. Это слишком много. В результате написал на Java.
Немного о вопросе «Почему на Java?». Детали производительности опишу потом. Если коротко — на простом не ООП коде, только арифметика и циклы — C++ с оптимизацией О3 или такой же скорости, или до +30% быстрее. Просто сейчас я лучше разбираюсь в Java, интерфейсе и работе с графикой.
FDTD – детальнее
Теперь перейдем к коду. Попытаюсь показать все, с объяснениями задачи и алгоритма. В двумерном случае система уравнений Максвелла распадается на две независимых подсистемы — ТЕ и ТМ волны. Код показан для ТЕ. Имеются 3 компоненты — электрическое поле Ez и магнитные Hx, Hy. Для упрощения время имеет размерность метров.
Изначально я думал, что от float смысла нет, так как все вычисления приводятся к double. Поэтому приведу код для double — в нем меньше лишнего. Все массивы имеют размеры +1, чтоб индексы совпадали с матрицами Матлаба (от 1, а не от 0).
Где-то в начальном коде:
public static int nx = 4096;// ширина области. Степень 2 для Фурье.
public static int ny = 500;// длина областиОсновной метод:
public static double[][] callFDTD(int nx, int ny, String method) {
int i, j;// индексы для циклов
double x; //метрическая координата
final double lambd = 1064e-9; // Длина волны в метрах
final double dx = lambd / 15; // размер шага сетки. Максимум ?/10. Чем меньше, тем выше точность.
final double dy = dx; //реально в коде не используется. Ячейки квадратные
final double period = 2e-6; // поперечный период решетки фотонного кристалла
final double Q = 1.0;// специфическое отношение
final double n = 1;// минимальный показатель преломления кристалла
final double prodol = 2 * n * period * period / lambd / Q; //продольный период
final double omega = 2 * PI / lambd; // циклическая частота световой волны
final double dt = dx / 2; // шаг по времени. НЕ больше, чем по координате
final double tau = 2e-5 * 999;// время затухания источника света. Нужно для запуска коротких импульсов. Если большое, затухание незаметно.
final double s = dt / dx; //отношение шага по времени и пространству
final double k3 = (1 - s) / (1 + s);// для граничных условий
final double w = 19e-7;// полуширина гауссова пучка
final double alpha = sin(0.0 / 180 * PI);// угол лазерного пучка от нормали. В радианах.
double[][] Ez = new double[nx + 1][ny + 1];
double[][] Hx = new double[nx][ny]; // основные массивы полей
double[][] Hy = new double[nx][ny];final int begin = 10; // координата, где пустота сменяется кристаллом. Без необходимости много не ставить.
final double mod = 0.008 * 2;//максимальная глубина модуляции диэлектрической проницаемости = 2*?n;
final double ds = dt * dt / dx / dx;// константа для подгона систем исчисленияИнициализация диэлектрической проницаемости (решетка кристалла). Точнее, обратная величина с константами. Используется дискретная функция (0 или 1). Это мне кажется ближе к реальным образцам. Конечно, сюда можно написать что угодно:
double[][] e = new double[nx + 1][ny + 1];
for (i = 1; i < nx + 1; i++) {
for (j = 1; j < ny + 1; j++) {
e[i][j] = ds / (n + ((j < begin) ? 0 : (mod / 2) * (1 + signum(-0.1 + cos(2 * PI * (i - nx / 2.0 + 0.5) * dx / period) * sin(2 * PI * (j - begin) * dy / prodol)))));
}
}Решетка кристалла выглядит примерно так:

Массивы, используемые для граничных условий:
double[][] end = new double[2][nx + 1];
double[][] top = new double[2][ny + 1];
double[][] bottom = new double[2][ny + 1];Предел счета по времени. Поскольку у нас шаг dt = dx / 2, стандартный коэффициент 2. Если среда плотная, или нужно идти под углом — больше.
final int tMax = (int) (ny * 2.2);Начинаем главный цикл:
for (int t = 1; t <= tMax; t++) {
double tt = Math.min(t * s + 10, ny - 1);Переменная tt тут учитывает ограничение скорости света, с небольшим запасом. Мы будем считать только ту область, куда свет мог дойти.
Вместо комплексных чисел я считаю отдельно две компоненты — синус и косинус. Я подумал, что для скорости лучше скопировать кусок, чем делать выбор внутри цикла. Возможно, заменю на вызов функции или лямбду.
switch (method) {
case "cos":
for (i = 1; i <= nx - 1; i++) {
x = dx * (i - (double) nx / 2 + 0.5); // поперечная координата в метрах
Ez[i][1] = exp(-pow(x, 2) / w / w - (t - 1) * dt / tau) * cos((x * alpha + (t - 1) * dt) * omega);
}
break;case "sin":
for (i = 1; i <= nx - 1; i++) {
x = dx * (i - (double) nx / 2 + 0.5);
Ez[i][1] = exp(-pow(x, 2) / w / w - (t - 1) * dt / tau) * sin((x * alpha + (t - 1) * dt) * omega);
}
break;
}Тут у нас на вход области (в крайнюю левую координату) поступает гауссов луч полуширины w, под углом alpha, осцилирующий во времени. Именно так и возникает «лазерное» излучение нужной нам частоты/длины волны.
Дальше копируем временные массивы под поглощающие граничные условия Мура:
for (i = 1; i <= nx; i++) {
end[0][i] = Ez[i][ny - 1];
end[1][i] = Ez[i][ny];
}
System.arraycopy(Ez[1], 0, top[0], 0, ny + 1);
System.arraycopy(Ez[2], 0, top[1], 0, ny + 1);
System.arraycopy(Ez[nx - 1], 0, bottom[0], 0, ny + 1);
System.arraycopy(Ez[nx], 0, bottom[1], 0, ny + 1);Теперь переходим к главному вычислению — следующему шагу по полю. Особенность уравнений Максвелла — изменение во времени магнитного поля зависит только от электрического, и наоборот. Это позволяет написать простую разностную схему. Исходные формулы были такие:
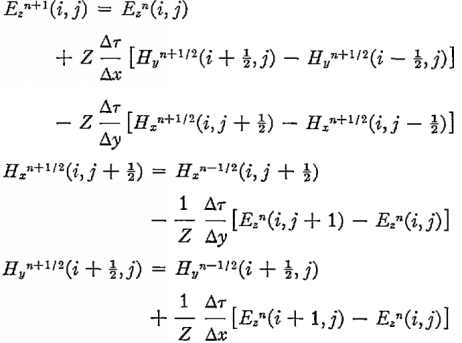
Все лишние константы я пересчитал заранее, заменил размерность Н, внес и учел диэлектрическую проницаемость. Поскольку оригинальные формулы для сетки, сдвинутой на 0,5, нужно не ошибиться с индексами массивов Е и Н. они разной длины — Е на 1 больше.
Цикл по области для Е:
for (i = 2; i <= nx - 1; i++) {
for (j = 2; j <= tt; j++) {//можно ли тут оптимизировать порядок доступа к ячейкам?
Ez[i][j] += e[i][j] * ((Hx[i][j - 1] - Hx[i][j] + Hy[i][j] - Hy[i - 1][j]));
}
}А теперь наконец-то применяем граничные условия. Они нужны потому, что разностная схема не считает крайние ячейки — для них нет формул. Если ничего не делать, свет будет отражаться от стенок. Поэтому применяем метод, минимизирующий отражение при нормальном падении. Обрабатываем три стороны — верх, низ и право. Потери производительности на граничные условия около 1% (тем меньше, чем больше задача).
for (i = 1; i <= nx; i++) {
Ez[i][ny] = end[0][i] + k3 * (end[1][i] - Ez[i][ny - 1]);//end
}
for (i = 1; i <= ny; i++) {
Ez[1][i] = top[1][i] + k3 * (top[0][i] - Ez[2][i]);//verh kray
Ez[nx][i] = bottom[0][i] + k3 * (bottom[1][i] - Ez[nx - 1][i]);
}Слева граница особая — в ней генерится луч. Также, как в прошлый раз. Просто на 1 шаг дальше по времени.
switch (method) {
case "cos":
for (i = 1; i <= nx - 1; i++) {
x = dx * (i - (double) nx / 2 + 0.5);
Ez[i][1] = exp(-pow(x, 2) / w / w - (t - 1) * dt / tau) * cos((x * alpha + t * dt) * omega);
}
break;
case "sin":
for (i = 1; i <= nx - 1; i++) {
x = dx * (i - (double) nx / 2 + 0.5);
Ez[i][1] = exp(-pow(x, 2) / w / w - (t - 1) * dt / tau) * sin((x * alpha + t * dt) * omega);
}
break;
}Осталось только посчитать магнитное поле:
for (i = 1; i <= nx - 1; i++) { // main Hx Hy
for (j = 1; j <= tt; j++) {
Hx[i][j] += Ez[i][j] - Ez[i][j + 1];
Hy[i][j] += Ez[i + 1][j] - Ez[i][j];
}
}
} // конец 3-мерного цикла.И еще мелочи: передать конечный отрезок для вычисления преобразования Фурье — нахождения картины в дальней зоне (пространство направлений):
int pos = method.equals("cos") ? 0 : 1; //какую из компонент записывать
BasicEx.forFurier[pos] = new double[nx]; //там в коде массив для Фурье
int endF = (int) (ny * 0.95);// произвольная координата в конце
for (i = 1; i <= nx; i++) {
BasicEx.forFurier[pos][i - 1] = Ez[i][endF];
for (j = 1; j <= ny; j++) {
Ez[i][j] = abs(Ez[i][j]);// ABS
} //я вот сейчас понял, что брать модуль не надо - я потом беру квадарат
}
Hx = null; //я верю, что это очистит память
Hy = null;
e = null;
return Ez;
} for (int i = 0; i < nx + 1; i++) {
for (int j = 0; j < ny + 1; j++) {
co.E[i][j] = co.E[i][j] * co.E[i][j] + si.E[i][j] * si.E[i][j];
}
}Отдельно берем преобразование Фурье:
fft.fft(forFurier[0], forFurier[1]);Поскольку в быстром Фурье не разбираюсь, взял первый попавшийся. Минус — ширина только степень двойки.
О производительности
Переходим к самому интересному для меня — что хорошего мы получили, перейдя с Матлаба на Java. В Матлабе я в свое время оптимизировал все, что смог. В Java — в основном внутренний цикл (сложность n^3). У Матлаба уже учтено то, что он считает сразу две компоненты. Скорость на первом этапе (больше — лучше):
| Matlab | 1 |
| Matlab матричный | 3,4 |
| Java double | 50 |
| C++ gcc double | 48 |
| C++ MSVS double | 55 |
| C++ gcc float | 73 |
| C++ MSVS float | 79 |
UPD. Добавил результат Матлаба, в котором двойные циклы заменил на вычитание матриц.
Опишем основных участников состязания.
- Matlab — 2011b и 2014. Переход на 32-битные числа дает очень малый прирост скорости.
- Java — вначале 7u79, но в основном 8u102. Мне показалось, что 8 немного лучше, но детально не сравнил.
- Microsoft VisualStudio 2015 конфигурация release
- MinGW, gcc 4.9.2 32 bit, декабрь 2014, всегда оптимизация O3. march=core i7, без AVX. AVX у меня на ноуте нет, там где есть прироста не давал.
- Pentium 2020m 2.4 GHz, ddr3-1600 1 канал
- Core i5-4670 3.6–3.8 GHz, ddr3-1600 2 канала
- Core i7-4771 3.7–3.9 GHz, ddr3-1333 2 канала
- Athlon x3 3.1 GHz, ddr3-1333, очень медленный контролер памяти.
2-ядерный этап
Вначале я считал ТЕ и ТМ компоненты последовательно. Кстати, это единственный вариант при нехватке памяти. Потом написал два потока — простые Runnable. Вот только прогресса была мало. Всего на 20-22% быстрее, чем 1-поточное. Начал искать причины. Потоки работали нормально. 2 ядра стабильно грузились на 100%, не давая жить ноуту.
Потом я посчитал производительность. Получилось, что она упирается в скорость оперативной памяти. Код уже работал на пределе чтения. «Пришлось» переходить на float. Проверка точности показала, что никаких смертельных погрешностей нет. Визуальной разницы однозначно нет. Суммарная энергия отличалась в 8 знаке. После интегрального преобразования максимум спектра — на 0,7e-6.
Но главное — получил рывок производительности. Общий эффект от 2 ядер и перехода на float +87–102%. (Чем быстрее память и больше ядер, тем лучше прирост). Athlon x3 дал мало прироста.
Реализация на С++ аналогичная — через std::thread (смотри в конце).
Текущие скорости (2 threads):
| Java double | 61 |
| Java float | 64-101 |
| C++ gcc float | 87-110 |
| C++ gcc 6.2 64 native | 99-122 |
| Visual Studio | 112-149 |
(новые компиляторы дают очень высокую, по сравнению с Java, производительность на 16384. Java и GCC-4.9 32 при этом проваливаются).
Все оценки проводились для однократного запуска расчета. Потому-что, если повторно запускать из GUI, не закрывая программу, дальше скорость возрастает. Имхо, jit-оптимизация рулит.
4-ядерный этап
Мне казалось, что еще есть куда ускоряться. Я принялся за 4-поточный вариант. Суть — область делится пополам и считается в 2 потоках, вначале по Е, потом по Н.
Вначале написал его на Runnable. Получилось ужасно — ускорение было только для очень большой ширины области. Слишком большие затраты на порождение новых потоков. Потом освоил java.util.concurrent. Теперь у меня был фиксированный пул потоков, которым давались задания:
public static ExecutorService service = Executors.newFixedThreadPool(4);
//……
cdl = new CountDownLatch(2);
NewThreadE first = new NewThreadE(Ez, Hx, Hy, e, 2, nx / 2, tt, cdl);
NewThreadE second = new NewThreadE(Ez, Hx, Hy, e, nx / 2 + 1, nx - 1, tt, cdl);
service.execute(first);
service.execute(second);
try {
cdl.await();
} catch (InterruptedException ex) {
} cdl = new CountDownLatch(2);
NewThreadH firstH = new NewThreadH(Ez, Hx, Hy, 1, nx / 2, tt, cdl);
NewThreadH secondH = new NewThreadH(Ez, Hx, Hy, nx/2+1, nx-1, tt, cdl);
service.execute(firstH);
service.execute(secondH);
try {
cdl.await();
} catch (InterruptedException ex) {
}Внутри потока выполняются пол цикла.
public class NewThreadE implements Runnable {
float[][] Ez;
float[][] Hx;
float[][] Hy;
float[][] e;
int iBegin;
int iEnd;
float tt;
CountDownLatch cdl;
public NewThreadE(float[][] E, float[][] H, float[][] H2, float[][] eps,
int iBegi, int iEn, float ttt, CountDownLatch cdl) {
this.cdl = cdl;
Ez = E;
Hx = H;
Hy = H2;
e = eps;
iBegin = iBegi;
iEnd = iEn;
tt = ttt;
}
@Override
public void run() {
for (int i = iBegin; i <= iEnd; i++) { // main Ez
for (int j = 2; j <= tt; j++) {
Ez[i][j] += e[i][j] * ((Hx[i][j - 1] - Hx[i][j] + Hy[i][j] - Hy[i - 1][j]));
}
}
cdl.countDown();
}
}Аналогичный класс для Н — просто другие границы и свой цикл.
Теперь прирост от 4 потоков есть всегда — от 23 до 49% (.jar). Чем меньше ширина, тем лучше — судя по скорости, мы влезаем в кеш-память. Наибольшая польза будет, если считать длинные узкие задачи.
| Java float 4потока | 86–151 |
| C++ gcc float 4потока | 122–162 (ближе 128) |
| C++ gcc 6.2 64 native | 124–173 |
| Visual Studio | 139–183 |
Реализация на С++ пока содержит только простые std::thread. Поэтому для нее чем шире, тем лучше. Ускорение С++ от 5% при ширине 1024 до 47% на 16384.
UPD. Добавил результаты GCC 6.2-64 и VisualStudio. VS быстрее старого GCC на 13–43%, нового на 3–11%. Главные фишки 64-битных компиляторов — более быстрая работа на широких задачах. Также, поскольку Java лучше распараллеливается на малых задачах (кеш), а С++ на широких — на широких задачах Visual Studio на 61% быстрее Джавы.
Как мы видим, в самом лучшем случае прирост Java 49% — как почти 3 ядра. Поэтому имеем забавный факт — при малых задачах лучше всего ставить newFixedThreadPool(3);
Для больших — по количеству потоков в процессоре — 4 или 6-8. Укажу еще забавный факт. На Атлоне х3 был очень слабый прогресс от перехода на float и 2 потоков — 32% от обеих оптимизаций. Прирост от «4»-ядерного кода на С++ также невелик — 67% между 1 и 4 ядрами (оба float). Списывать можно на медленный контролер памяти и 32-битную Винду.
Но 4-ядерный Java-код отработал отлично. При 3 потоках Екзекутора +50,2% от 2-ядерной версии для больших задач. Почему-то худшая 2-ядерная реализация усилилась максимально возможной многоядерной.
Последнее замечание по 4-ядерному коду в Java. Текущие затраты времени:
| Основные 2-мерные циклы Е и Н | 83% |
| Прочее, считая начальную инициализацию всего | 16% |
| Порождение (4) потоков | Около 1% (0,86 по профилировщику) |
Я постарался максимально оптимизировать основные циклы, думая что остальное тратит мало времени.
Выкладываю также полный код 4-ядерного случая на С++:
#include <iostream>
#include <complex>
#include <stdio.h>
#include <sys/time.h>
#include <thread>
using namespace std;
void thE (float** &Ez, float** &Hx, float** &Hy, float** &e,
int iBegin, int iEnd, int tt)
{
for (int i = iBegin; i <= iEnd; i++) // main Ez
{
for (int j = 2; j <= tt; j++)
{
Ez[i][j] += e[i][j] * ((Hx[i][j - 1] - Hx[i][j] + Hy[i][j] - Hy[i - 1][j]));
}
}
}
void thH (float** &Ez, float** &Hx, float** &Hy,
int iBegin, int iEnd, int tt)
{
for (int i = iBegin; i <= iEnd; i++)
{
for (int j = 1; j <= tt; j++)
{
Hx[i][j] += Ez[i][j] - Ez[i][j + 1];
Hy[i][j] += Ez[i + 1][j] - Ez[i][j];
}
}
}
void FDTDmainFunction (char m)
{
//m=c: cos, else sin
int i,j;
float x;
const float dx=0.5*1e-7/1.4;
const float dy=dx;
const float period=1.2e-6;
const float Q=1.5;
const float n=1;//ne используется в Эпсилон матрице пока =1
const float lambd=1064e-9;
const float prodol=2*n*period*period/lambd/Q;
const int nx=1024;
const int ny=700;
float **Ez = new float *[nx+1];
for (i = 0; i < nx+1; i++)
{
Ez[i] = new float [ny+1];
for (j=0; j<ny+1; j++)
{
Ez[i][j]=0;
}
}
float **Hx = new float *[nx];
for (i = 0; i < nx; i++)
{
Hx[i] = new float [ny];
for (j=0; j<ny; j++)
{
Hx[i][j]=0;
}
}
float **Hy = new float *[nx];
for (i = 0; i < nx; i++)
{
Hy[i] = new float [ny];
for (j=0; j<ny; j++)
{
Hy[i][j]=0;
}
}
const float omega=2*3.14159265359/lambd;
const float dt=dx/2;
const float s=dt/dx;//for MUR
const float w=40e-7;
const float alpha =tan(15.0/180*3.1416);
float** e = new float *[nx+1];
for (i = 0; i < nx+1; i++)
{
e[i] = new float [ny+1];
for (j=0; j<ny+1; j++)
{
e[i][j]=dt*dt / dx/dx/1;
}
}
const int tmax= (int) ny*1.9;
for (int t=1; t<=tmax; t++)
{
int tt=min( (int) (t*s+10), (ny-1));
if (m == 'c')
{
for (i=1; i<=nx-1; i++)
{
x = dx*(i-(float)nx/2+0.5);
Ez[i][1]=exp(-pow(x,2)/w/w)*cos((x*alpha+(t-1)*dt)*omega);
}
}
else
{
for (i=1; i<=nx-1; i++)
{
x = dx*(i-(float)nx/2+0.5);
Ez[i][1]=exp(-pow(x,2)/w/w)*sin((x*alpha+(t-1)*dt)*omega);
}
}
std::thread thr01(thE, std::ref(Ez), std::ref(Hx), std::ref(Hy), std::ref(e), 2, nx / 2, tt);
std::thread thr02(thE, std::ref(Ez), std::ref(Hx), std::ref(Hy), std::ref(e), nx / 2 + 1, nx - 1, tt);
thr01.join();
thr02.join();
// H
for (i=1; i<=nx-1; i++)
{
x = dx*(i-(float)nx/2+0.5);
Ez[i][1]=exp(-pow(x,2)/w/w)*cos((x*alpha+t*dt)*omega);
}
std::thread thr03(thH, std::ref(Ez), std::ref(Hx), std::ref(Hy), 1, nx / 2, tt);
std::thread thr04(thH, std::ref(Ez), std::ref(Hx), std::ref(Hy), nx / 2 + 1, nx - 1, tt);
thr03.join();
thr04.join();
}
}
int main()
{
struct timeval tp;
gettimeofday(&tp, NULL);
double ms = tp.tv_sec * 1000 + (double)tp.tv_usec / 1000;
std::thread thr1(FDTDmainFunction, 'c');
std::thread thr2(FDTDmainFunction, 's');
thr1.join();
thr2.join();
gettimeofday(&tp, NULL);
double ms2 = tp.tv_sec * 1000 + (double)tp.tv_usec / 1000;
cout << ms2-ms << endl;
return 0;
}delete[] пока нет, потому что нужно же результат где-то использовать :)
Это самый простой код, без нормальной решетки и граничных условий. Интересно, можно ли в С++ эффективнее объявлять 2-мерные массивы и вызывать потоки?
8 ядер
А больше ядер у меня нет. Если бы мои задачи не упирались в память, делил бы дальше. Вроде, ThreadPool дает малые затраты. Или переходить на Fork-Join Framework.
Я мог бы проверить — отказаться от первых двух потоков, и делить одну задачу на 4-8 кусков на i7. Но смысл будет, только если кто-то протестирует на машине с быстрой памятью — DDR-4 или 4 канала.
Лучший способ избавиться от нехватки скорости памяти — видеокарты. Переходить на Cuda мне мешает брат, который запрещает обновлять видеодрайвер (незнание С и Cuda).
Итог и послесловия
Я могу быстро решить любую нужную мне 2-мерную задачу с хорошей точностью. Сетка 4096х2000 проходится на 4-ядернике за 106 секунд. Это будет 300 микрон х 40 слоев — максимальные образцы у нас.
В 2D при 32-битной точности требуется немного памяти — 4байта*4массива*2 комплексных компоненты = 32 байта / пиксель в худшем случае.
В 3D все намного хуже. Компонент уже шесть. Можно отказаться от двух потоков — считать компоненты последовательно и писать на винт. Можно не хранить массив диэлектрической проницаемости, а считать в цикле или обойтись очень маленьким периодическим участком. Тогда в 16 ГБ оперативы (максимум у меня на работе) влезет область 895х895х895. Это будет нормально «чтоб посмотреть». Зато считаться будет «всего» 6–7 часов один проход. Если задачу хорошо поделится на 4 параллельных потока. И если пренебречь вычислением ?.
Только для спектра мне не хватит. При ширине 1024 я не вижу необходимые детали. Нужно 2048. А это 200+ ГБ памяти. Поэтому трехмерный случай — это сложно. Если не разрабатывать код с кеширующими ССД.
P.S. Оценки скорости были довольно приблизительные. Я проверял Матлаб только на малых задачах. Сейчас проверил Java — задачу 2048*1976 (аналог 2000*2000) на 4-ядернике. Время расчета 45,5 секунд. Ускорение от Матлаба 141 раз (точно).
Возможные планы на будущее:
*) Проверить скорость чистого С (не ++). По benchmarksgame он всегда быстрее.
1) Проверить комплексные классы в С и Java. Может, в С они реализованы достаточно быстро. Правда, боюсь, все они будут больше 8 байт.
2) Закинуть все 2- и 4-ядерные версии в MSVS, найти настройки оптимизации.
3) Проверить, могут ли лябмды/стримы ускорить основной цикл или дополнителные.
4) Сделать нормальный GUI для выбора всего и визуализации результатов.
99) Написать Cuda-версию.
Если кому-то интересно, опишу FDTD и другие методы рассчетов, фотонные кристаллы.
На Github выложил 2 версии:
1) 2-поточная с зачатками интерфейса выбора параметров
2) 4-поточная
Обе рисуют картинку и спектр. Просто пока пиксель в пиксель — не берите ширину выше 2048. Еще умеют принимать размеры области из консоли.
Комментарии (96)

opaopa
10.01.2017 13:26Cтоит попробовать вынести константные подвыражения из циклов.
Судя по ограничению скоростью памяти, вам стоит попробовать учесть иерархию памяти, чтобы повысить локальность обращений к памяти (процент попадания в кэш).
https://habrahabr.ru/post/312078/
Далее -march=native, векторизация (-sse2, avx), интринсики, профайлеры…
После чего становится грустно и взоры обращаются обратно к ANSYS ;)vlanko
10.01.2017 13:36Не вижу возможности вынести из циклов. Все зависит от [i][j]
-march=native проверю.
Извините, я компилирую на одной, а проверяю на разных.
Использовался вроде ‘nehalem’, проверял что от ‘sandybridge’ пользы нет (проверю, по моему у меня опции не так называются)
В интринсиках разбираться не планирую
opaopa
10.01.2017 15:34Не вижу возможности вынести из циклов. Все зависит от [i][j]
да, да конечно. Я понимаю, что это не самый внутренний цикл, но сравнение строк… Будем молиться, что компилятор сам раздвоит циклы для разных case (о чем бы было неплохо ему напомнить явно). Уж лучше лямбды/указатели на ф-ии, виртуальные методы в явном виде. Накрайняк — глобальный копипаст (как обычно, это всего быстрее:) ).for (int t = 1; t <= tMax; t++) { // begin main loop float tt = Math.min(t * s + 10, ny - 1); //gauss switch (method) { case "cos":
в
я правильно понял, чтоforeach (i) x=f(i) exp(-pow(x, 2) / w / w - (t - 1) * dt / tau)
- вся правя часть изменяется-таки от i и x и не может быть вынесена из цикла? Что-то я не верю, что компилятор матан учил лучше меня. Или там приколы с потерей точности?
- pow(x, 2) это не x*x и вызов ф-ции (float,float) имеет смысл?
я Понимаю, что это вроде как мелкие придирки, но есть и более интересные замечания:
float **Hy = new float *[nx];
— массив указателей на массивы. Итого 2 обращения к памяти. Лучше уж глобальныйfloat XX[X][Y]
, что сведет операцию доступа к XX[x*Y+y]. Замечание: правильно назначьте X и Y, чтобы доступ к памяти был последовательным и хорошо ложился на prefetcher. И не надо бояться, что бинарник распухнет: эти массивы будут кратко описаны в сегменте zero-data.
Потом смотрим, что весь код у вас есть несколько циклов по nx при все увеличивающимся ny. Так мы имеем, что к следующему циклу по x строка уже выпала из кэша. Возможно имеет смысл сделать
for (int t = 1; t <= tMax; t++) { for (i = 1; i <= nx - 1; i++) { //gauss //для единственного i // boundary conditions //для единственного i ....
Да, там придется подумать, чтобы не сломать математику, но такова судьба программиста-оптимизатора: записать алгоритм совершенно нечитаемо.
Дальше. Как уже говорили нижеВсе зависит от [i][j]
, но не для всех (i,j), а некой окрестности точки (i,j), что позволяет как повысить попадания в кэш, так и подумать за уменьшение выделенной памяти и массовое распаралеливание.vlanko
10.01.2017 16:07Спасибо за анализ.
— Глобальный копипаст делать точно не хочу — слишком много нужно. Сделаю вызов функции или ссылку на функцию.
— exp(-pow(x, 2) — это какое-то локальное помутнение. Все квадраты расписал, а этот нет.
— exp( — (t — 1) * dt / tau), пожалуй, посчитаю заранее
— в С не шарю, именно об этом спрашивал. Но для Джавы 1-мерный массив давал проигрыш в производительности.
—for (i = 1; i <= nx — 1; i++) {
//gauss //для единственного i
// boundary conditions //для единственного i
Вот тут мы думаю потеряем больше, пытаясь поэлементно копировать граничные элементы.
— порядок циклов вроде правильно ложится в кеш.
— я попробовал дополнительно делить массив еще на 4 части, имеем небольшую потерю производительности.
vlanko
10.01.2017 13:46Еще моменты по оптимизации под 4 ядра. Я думал поделить массив пополам изначально, чтоб два потока обращались к разным учаскам памяти.

lgorSL
10.01.2017 13:52Если Вы упираетесь в скорость памяти — попробуйте разбить задачу на кусочки по-другому. Например, можно взять область (100+2x, 100+2x), и на её основе посчитать вперёд сразу на х шагов центральный кусочек размером 100*100. В идеале должно получаться, чтобы необходимая для "кусочка" память была не слишком большой и помещалась в кеш процессора — тогда у Вас на первом шаге будет чтение из ram и на следующих (х-1) шагах будет использоваться кеш.
vlanko
10.01.2017 14:05Понял вашу мысль. Думаю, ничего хорошего не выйдет. Слишком большие накладные расходы на 2х.
это невозможно. Нельзя выделить какой-то кусок и считать его больше одного шага. Каждая точка на следующем шаге зависит от четырех соседних.
Можно только попытаться разбить циклы внутри одного шага.
lgorSL
11.01.2017 00:43нет, если взять х небольшим, то должно работать быстрее.
Например, для x=5 Вы рассчитаете квадраты размерами 110, 108,… 102. Конечно,
это немного больше вычислений по сравнению с вычислениями и чтением данных из 5 квадратов 102*102, (процентов на ~20%), но нагрузка на оперативную память упадёт почти в 5 раз — а именно она и является бутылочным горлышком.

Videoman
10.01.2017 16:28+3Безотносительно самой задачи — код на С++ просто безумен. Уже много раз повторяли, в том числе и здесь, на habr-e, что нельзя сравнивать Java и С++ просто переведя алгоритм на уровне синтаксиса. Ни один вменяемый программист на С++ такую программу не напишет. Оператор new в Java и С++ не являются эквивалентами и new в с++ используется совсем по другому. Обращение с двумерным массивом поэлементно через два индекса первый из которых прыгает по таблице указателей это вообще за гранью.

Deosis
11.01.2017 07:24На Хабре пишут, что многие научные расчеты пишут на фортране.
Даст ли выигрыш переписывание и оптимизация на него?vlanko
11.01.2017 09:42Кроме того, что в Фортране я совершенно не разбираюсь.
На Фортране пишут потому, что под него есть тонны математических/научных библиотек
https://benchmarksgame.alioth.debian.org/u64q/fortran.html
Фортран или на уровне чистого С, или медленнее.
vlanko
11.01.2017 10:18Уточняю. Нашел книжку 2006года по распараллеливанью.
Там ФДТД используют на Fortran 90 с MPI

Videoman
11.01.2017 11:57Не даст. Фортран просто имеет более высокоуровневые оптимизированные абстракции для работы с математикой. Т.е. на нем есть уже готовые примитивы, например для работы с матрицами, из «коробки». Основная причина использования фортрана для расчетов, это то, что он старше С и на нем написано куча библиотек для научных расчетов, а математики и физики очень консервативны, и, в основном, не любят программирование.

Regis
10.01.2017 19:02+13) Проверить, могут ли лябмды/стримы ускорить основной цикл или дополнителные.
Не помогут. Лямбды и стримы — чтобы сделать код более удобным. В лучшем случае вы получите приблизительно такой же native-код с той же производительностью. В худшем случае — всё станет заметно медленнее.

Regis
10.01.2017 19:21Возможно некоторые циклы, в которых есть обращение к нескольким строкам, будет эффективнее разбить на несколько проходов, где идут обращения только к одной строке.
Например вместо одного прохода со строчкой
Ez[i][j] += e[i][j] * ((Hx[i][j — 1] — Hx[i][j] + Hy[i][j] — Hy[i — 1][j]));
сделать два прохода:
1:
Ez[i][j] += e[i][j] * ((Hx[i][j — 1] — Hx[i][j] + Hy[i][j]));
2:
Ez[i][j] -= e[i][j] * Hy[i — 1][j];
Regis
10.01.2017 19:23… а возможно даже и 3, чтобы одновременно участвовало меньше матриц:
1.
Ez[i][j] += e[i][j] * ((Hx[i][j — 1] — Hx[i][j]));
2.
Ez[i][j] += e[i][j] * Hy[i][j];
3.
Ez[i][j] -= e[i][j] * Hy[i — 1][j];vlanko
10.01.2017 19:57Проверил такую идею. Производительность упала в 1,6 раз
Отличная оценка, спасибо за неудачную идею.
В таком способе нужно читать эпсилон 3 раза.
Вместо 5 чтений 7+лишение записи. Плюс лишняя математика.
А в Н такого и не сделаешь
Regis
11.01.2017 01:34Раз производительность упала в 1.6 раз, а не в 3, значит вы именно упираетесь по памяти и вам стоит изучить варианты реструктурирования ваших циклов. В идеале — добиться векторизации всего, что только можно.

Videoman
11.01.2017 12:13Основная идея для оптимизации в вашем коде, если не брать векторизацию и развертывание, это вынести из внутренних циклов все константные данные. Например в таком коде:
void thH (float** &Ez, float** &Hx, float** &Hy, int iBegin, int iEnd, float tt) { for (int i = iBegin; i <= iEnd; i++) { for (int j = 1; j <= tt; j++) { Hx[i][j] += Ez[i][j] - Ez[i][j + 1]; Hy[i][j] += Ez[i + 1][j] - Ez[i][j]; } } }
можно сделать так:
void thH (float**& Ez, float**& Hx, float**& Hy, int iBegin, int iEnd, float tt) { for (int i = iBegin; i <= iEnd; i++) { float* Ez_row = Ez[i]; float* Ez_row_plus1 = Ez[i + 1]; float* Hx_row = Hx[i]; float* Hy_row = Hy[i]; for (int j = 1; j <= tt; j++) { Hx_row[j] += Ez_row[j] - Ez_row[j + 1]; Hy_row[j] += Ez_row_plus1[j] - Ez_row[j]; } } }vlanko
11.01.2017 15:20После компиляции бинарник мало отличается. Разница производительности в пределах погрешности.

Videoman
11.01.2017 15:47Замечательно, значит одно из двух:
1. Hotpoint не там и основное время тратится не в «основном» цикле
2. Компилятор сам сделал эту оптимизацию
А вы пробовали избавиться от new в циклах? И не совсем понял, вы какой профилировщик используете в С++?vlanko
11.01.2017 16:011. Два основных цикла тратят до 84-85% времени (на Джаве также)
2. Да, компиляторы нынче умные
Профилировщик в С++ никакой, хотя вроде в VisualStudio смотрел.
Videoman
11.01.2017 17:46Посмотрел в профайлере VS действительно, тормозят основные циклы, причем в них делаются простые вычисления. Развертка цикла ничего не дает у меня на машине. Значит тормозит память и нужно попытаться изменить layout матриц.
Как идея, сделать все данные более локальными. Например:
1. Сделать одну матрицу вместо 4-х где хранить коэффициенты друг за другом или как структуру.
2. Сделать одномерный массив и руками интерировать по строкам.vlanko
11.01.2017 17:532.У меня и у https://habrahabr.ru/post/319216/#comment_10005284
1-мерный массив уменьшает производительность.
1. А вот хранить все локально — интересный вариант. Только все циклы придется ужасно переписывать.
Videoman
11.01.2017 18:51Попробовал одномерный массив — подтверждаю. Ничего не дает.
Ради прикола, попробовал заменить в одномерной версии float* на char* (понимаю что считать будет не правильно) — выигрыш всего 25%. Плюс, 700 * sizeof(char) * 1024 = 700кб — это смешно по памяти (не похоже на память). Значит вам нужна векторизация, он просто не успевает считать.
К сожалению это специфично для компилятора и сами матрицы должны быть выровнены. Быстро не проверить.vlanko
11.01.2017 22:28Сделал еще экстремальнее — заменил 4 массива на int8_t (или это плохой тип?), с сохранением корректности всей математики. Выигрыш при 4096х700 1,26 раза. Чем больше область, тем выше.
Почему же был высокий прирост от 64бита к 32?
1024*700 — это тестовая задача, какую смог дождаться в Матлабе. С++ детально не изучал, в Джаве наибольший упор в скорость памяти при 4096х500

Videoman
11.01.2017 22:23Еще мысли:
Все выглядит так, как-будто циклы просто очень медленно считаются, хотя тела маленькие и операции элементарны. Здесь хорошо бы помог VTune Analizer или что-то подобное. У меня его к сожалению нет, а профайлер от Microsoft очень грубый, он показывает сколько CPU затрачивает строчка кода, но при этом нельзя посмотреть ассемблерный код. VTune в таких случаях показывает более точную информацию. Может быть у вас где-то зависимость по данным и вся параллелизация убивается на корню.vlanko
11.01.2017 23:33Провел собственный анализ.
Много тратит запись элемента массива. Если принять время выполнения 3 циклов за 100у.е., то
каждая запись(+=) из 3х тратит 20,
запись на даблах 31 (просто для сравнения)
однократное чтение 6-7
пятикратное чтение 27
(оценки приблизительны, внимательный читатель поймет, что мы уже ниже 0)
Videoman
12.01.2017 00:02Ох, а как вы это померили? Дело в том, что современные процессоры очень сложно устроены и при перетасовке операций (при аналогичном результате) результаты могут быть совсем другими. Идея ж простая (теоретически): есть X — исполнительных блоков, способных работать одновременно), плюс Y — стадий конвейера. Если операции без зависимостей друг от друга, то пропускная способность будет XY, если каждая операция зависит от другой, то способность будет 1 (все условно). Только вот по С — коду понять, где затык не всегда можно. А мерить время сами операции бесполезно, важно только суммарное время.
vlanko
12.01.2017 12:39Еще вычитал:
«Согласно протоколам согласованности кеша (cache coherence protocols), если ядро пишет в кеш-строку, то строка в другом ядре, ссылающаяся на ту же память, признаётся недействительной (пробуксовка кеша, cache trashing). В результате при каждой операции записи возникают блокировки памяти.»
У меня такое возможно на середине массива. То есть задача влазит в кеш, но пишется с проблемами.
Videoman
12.01.2017 12:50Все верно, но у вас такого не будет, так как, пока первое ядро дойдет до середины второе уже вытеснит все строки кеша и будет обрабатывать конец второй половины. Ваш алгоритм должен работать в 50 раз быстрее, при правильной оптимизации. Вот у меня, на той же машине есть цикл в 10 раз сложнее, а молотит в 10 раз быстрее чем ваш.
P.S. У вас нет случайно ссылки на ваш проект под студию, а-то я нечаянно похерил свой?vlanko
12.01.2017 12:53Я ленивый, делал только ГСС.
Под студию был 1-ядерный.
Постараюсь сегодня сделать 2-4.
Videoman
12.01.2017 13:24Одноядерный тоже пойдет для экспериментов. Обычно если потоки абсолютно не пересекаются, то их общая производительность просто суммируется.
vlanko
12.01.2017 20:52Мой старый проект завален какими-то левыми файлами, создал чистый 4-ядерный.
https://cloud.mail.ru/public/8K8G/VCRZSJQTt
Есть профит по сравнению с ГСС во всех случаях.
Скоро обновлю в статье
Videoman
13.01.2017 12:03Спасибо! Попробую с главными циклами поэксперементировать. Жалко что у вас код не С++. Было бы проще и быстрее его менять, а так сплошное дублирование. Меня не покидает ощущение что я погрузился в средние века. Уж очень к С++ быстро привыкаешь.

Torvald3d
11.01.2017 16:53Не обязательно выносить общие вычисления за пределы циклов — компилятор с этим замечательно справляется. Тоже самое касается констант

Videoman
11.01.2017 17:01Смотря какой. Вот я сейчас смотрю профайлером. У меня VS 2013 c компилятором по умолчанию. Она ничего не выносит в коде автора. У меня вообще код падает, так как в главном цикле идет сравнение с tt которое float и в зависимости от причуд плавающей арифметики периодически происходит выход за границы массива.
vlanko — в С++ код при смешивании типов приводится к более общему типу, т.е. j приводится к floatvlanko
11.01.2017 17:08да, float — это мой глюк. Пока циклы были <, а не <= все было нормально. Заменю все на инт.

Torvald3d
10.01.2017 22:34Какой у вас суровый брат. А что, если поставить еще одну ОС рядышком со своим набором драйверов (CUDA)? Или там какие то другие причины?
Касаемо кода с++, по беглому просмотру, он конечно нуждается в оптимизации и, главное, в векторизации. Можно воспользоваться готовыми библиотеками с векторными классами, например eigen. Если будет время, обязательно посмотрю во что там компилируется этот код, выносятся ли условия за пределы цикла, векторизует ли код компилятор.
Кстати, а Java умеет векторизовать?
Torvald3d
11.01.2017 00:34Ускорил код более чем в два раза просто развернул «горячие» циклы:
что былоvoid thE (float** &Ez, float** &Hx, float** &Hy, float** &e, int iBegin, int iEnd, float tt) { for (int i = iBegin; i <= iEnd; i++) // main Ez { for (int j = 2; j <= tt; j++) { Ez[i][j] += e[i][j] * ((Hx[i][j - 1] - Hx[i][j] + Hy[i][j] - Hy[i - 1][j])); } } } void thH (float** &Ez, float** &Hx, float** &Hy, int iBegin, int iEnd, float tt) { for (int i = iBegin; i <= iEnd; i++) { for (int j = 1; j <= tt; j++) { Hx[i][j] += Ez[i][j] - Ez[i][j + 1]; Hy[i][j] += Ez[i + 1][j] - Ez[i][j]; } } }vlanko
11.01.2017 09:47Спасибо, буду смотреть
Скажите нубу, что делает это
asm("# point 2 start");
?
Torvald3d
11.01.2017 10:58Абсолютно ничего, это просто метка/комментарий для ассемблерного кода. Если скомпилить с флагом -S, то рядом с ехешником создастся файл с расширением .s — в нем будет ассемблерный код, то, во что преобразовывает компилятор исходники. Метка # point 2 start нужна для того, чтобы быстренько найти этот участок в асм коде. Вот, например:
Какой-то кусок кода на с++int j3 = j+2; int j4 = j+3; asm("# point 2 sum1 start"); sum1[0] = Hx[i][j1 - 1] - Hx[i][j1]; sum1[1] = Hx[i][j2 - 1] - Hx[i][j2]; sum1[2] = Hx[i][j3 - 1] - Hx[i][j3]; sum1[3] = Hx[i][j4 - 1] - Hx[i][j4]; asm("# point 2 sum1 end"); sum2[0] = Hy[i][j1] - Hy[i - 1][j1]; sum2[1] = Hy[i][j2] - Hy[i - 1][j2];vlanko
11.01.2017 12:02Ахтунг!
Применил ваш код, и вышла фигня.
Потом понял:
ttt = tt / 4;
Вы просто уменьшили объем вычислений в 4 раза
Torvald3d
11.01.2017 16:56Я не уменьшал количество вычислений, я уменьшил количество итераций цикла в четыре раза, а в самом теле цикла увеличил в четыре раза. А фигня у вас получилась скорее всего изза того, что вы не обрабатываете данные на границах — я об этом писал.
vlanko
11.01.2017 17:16+1Вы уменьшили в 4 раза.
Я же посмотрел визуализацию на Яве. Фигня была именно в том, что обрабатывается только первая четверть картинки.
В вашем коде:
auto ttt = tt / 4; for (int j = 2; j <= ttt; j+=4) { int j1 = j+0; int j2 = j+1; int j3 = j+2; int j4 = j+3;
Нужно:
а) int j1 = j * 4+0;
или б) j <= tt- 4
или в) j <= ttt * 4. (Но эти два варианта глупые)
В вашем коде максимальное значение переменных tt / 4+3 << tt
j <= ttt
ttt = tt / 4;

Torvald3d
11.01.2017 17:03сравните два варианта кода:
for (int i = 0; i = 10; i++) a[i] = b[i] + c[i];
for (int i = 0; i = 10/4; i+=4) { a[i] = b[i] + c[i]; a[i+1] = b[i+1] + c[i+1]; a[i+2] = b[i+2] + c[i+2]; a[i+3] = b[i+3] + c[i+3]; }
Во втором случае я развернул цикл, но так как 10 итераций не делятся на цело на 4, то получается оставшиеся две итерации нужно обработать отдельно:
for (int i = 0; i = 10/4; i+=4) { a[i] = b[i] + c[i]; a[i+1] = b[i+1] + c[i+1]; a[i+2] = b[i+2] + c[i+2]; a[i+3] = b[i+3] + c[i+3]; } a[8] = b[8] + c[8]; a[9] = b[9] + c[9];
Этого я не сделал в вашем алгоритме, о чем сразу же и написал:
Разумеется, граничные условия нужно дообрабатывать отдельно или указывать границы кратные количеству развертываний цикла. Но это мелочи и на производительность практически никак не скажется.
Советую вам корректно развернуть циклы, так как потенциально это может дать сильный прирост производительности на больших итерацияхvlanko
11.01.2017 17:33+1В моем случае я вообще не вижу смысла в таком разворачивании циклов. У меня запас производительности процессора примерно в 48 раз выше, чем скорость памяти.
vlanko
11.01.2017 12:17Пока на Джаве разворачивание только Е дало падение производительности на 3 % (в пределах погрешности)

Torvald3d
11.01.2017 02:35vlanko, как выяснилось векторизовать данные циклы невозможно по причине смещения данных (Hx[i][j — 1] и Hx[i][j], например).
Но развертывание цикла, как я показал выше, вполне имеет место быть, у меня время просчета сократилось с 4500мс до 1900мс
Может быть возможно изменить алгоритм так, чтобы данные не пересекались — тогда можно будет векторизовать.
Victor_koly
12.01.2017 00:24По идее любая разностная схема считает производные именно как разницу между соседними элементами и обойти это никак не выйдет.

Torvald3d
11.01.2017 02:41Кстати, можно воспользоваться встроенными векторными классами
С ними так же просто, как в шейдерном коде. Если вам не удастся векторизовать ваш алгоритм, то и на CUDA особого прироста не ждите.

kosmos89
10.01.2017 23:55Проверить скорость чистого С (не ++). По benchmarksgame он всегда быстрее.
У вас код и так написан на почти чистом Си. Так что никакого прироста не получится.

Gribs
11.01.2017 00:28Извините, но почему не meep? Или любой другой коммерческий вариант (rsoft, lumeric)? Я понимаю что лицензирование коммерческих продуктов стоит денег, но было бы интересно сравнить ваш код с meepом.
Я понимаю что писать свой FDTD это занимательно (лично знаю человека который из принципа написал свой 2D FDTD на CUDA), но для исследовательских целей почему бы не использовать готовый продукт и не строить свой велосипед?
И еще по поводу Матлаба. Циклы и условные ветвления (а так же вызовы анонимных функций) в нем действительно медленные, но вот встроенные алгоритмы работы с массивами (сложение, умножение матриц, нахождение определителей, собственных значений и т.д.) давольно быстры. На мой первый взгляд в матлабе возможно реализовать FDTD используя только лишь один внешний цикл для времени, все остальное можно сделать используя матричные операции.vlanko
11.01.2017 00:32Когда я начинал разбираться в вопросе в 2010м, Meep был непонятно чем. Сейчас, наверное, использовать его оптимальнее, чем самому писать на С++.
Да, я писал. Матлаб очень быстро умножает матрицы и с нормальной скоростью берет функции от массивов. Возможно, получится такое сделать. Но это потребует создание 4 новых матриц для вычитания. Боюсь, со скоростью памяти будет хуже.
vlanko
11.01.2017 20:51Я переписал в Матлабе 2-мерный цикл полностью на вычитание матриц:
кодEz0(2:end-1, 2:tt) = Ez(2:end-1, 2:tt)+e(2:end-1, 2:tt).*(Hx(2:end, 1:tt-1)-Hx(2:end, 2:tt)+Hy(2:end, 2:tt)-Hy(1:end-1, 2:tt)); Hx0(1:end, 1:tt) = Hx(1:end, 1:tt) + dH *(Ez(1:end-1, 1:tt) - Ez(1:end-1, 2:tt+1)); Hy0(1:end, 1:tt) = Hy(1:end, 1:tt) + dH *(Ez(2:end, 1:tt) - Ez(1:end-1, 1:tt));
Gribs
11.01.2017 21:26Еще можно посмотреть в матлабовском профайлере что происходит (profile viewer). Я не пытаюсь сказать что маталб может провести все вычисления так же быстро как и си/ява, плюс возможно в матлабе не получится так просто сделать распараллеливание (если честно кроме parfor я не знаю других способов распаралелливания вычислений, хотя можно попробовать запускать ява код из матлаба). Но возможности матлаба по визуализации подкупают.
Если вы в лс опишите структуру и скажете что посчитать, я могу сделать .ctl файл для meep и прогнать вычисления.

Siemargl
11.01.2017 02:02Предлагаю начать с того, что параллелизация на с++ выполнена с ошибкой.
Видимо автором ожидается, что цикл по t ожидает завершения стартованных по join() нитей, но это не так.
Torvald3d
11.01.2017 02:28А чего бы ему не ожидать? join() блокирует текущий поток.

Siemargl
11.01.2017 03:09Теоретически да. Но я проверяю, и у меня полный бардак в порядке исполнения при использовании mingw-gcc

Siemargl
11.01.2017 03:39Уточняю. В исходном коде (и в Яве и в С++), заявленном как 4-х поточный, выполняется следующее
— запуск 2х потоков
— ожидание их завершения
— запуск еще 2х потоков
— ожидание их завершения
Какое может быть ускорение? Это обычный 2-поточный код
Torvald3d
11.01.2017 03:56Нет, не двухпоточный.
— запуск 2х потоков
— в каждом из двух потоков еще запуск по 2 потока
То есть два треда, в каждом запускаются сотни раз еще по паре тредов, в итоге одновременно запущено в среднем 4 потока.
Siemargl
11.01.2017 04:36Принято, похоже сплю.
В mingw действительно что то не так в потоках, некоторые версии mingw с потоками не работают совсем, некоторые абы как. В общем, принудительно поставив пару mutex'ов, заставил отработать как надо.
На результат не повлияло.
Простая замена на линейный массив [y + maxx *x] привела к большому падению скорости.
Дальше надо лезть в ассемблер.
И главный вопрос — почему при распараллеливании не растет пропорционально скорость?
FFT хорошая задача, еще в каком то старом тесте былаvlanko
11.01.2017 09:53Потоки — стандартные из C++11.
Именно в mingw нормально работают.
Да, одномерный массив у меня тоже давал падение скорости.
Имхо, ускорение слабое, потому что даже 2-поточный код близок к скорости памяти.

aso
11.01.2017 08:56Поскольку в быстром Фурье не разбираюсь, взял первый попавшийся. Минус — ширина только степень двойки.
Это стандартная особенность БПФ.
Вообще, последние i7 имеют от десяти до двадцати мег кэша L3 — хотя он тормознутее, конечно — но ограничение скорости по памяти должно быть слабее, чем для других.
А вообще, получается необходимо дробить алгоритм на отдельные «островки», хорошо попадающие в кэш.vlanko
11.01.2017 09:57А на БПФ я наезжаю потому, что Матлаб умеет как-угодно без существенных потерь скорости.
Да, но у моих процей только 6-8 МБ кеша.
Малые задачи у меня выполняются быстрее — эквивалент 30 ГБ/сек против 17 ГБ/сек, (память 20около).
То есть лезут в кеш.
Но тупое деление большой области на 4 куска по і делает немного хуже.
Буду проверять развернутые циклы.
aso
11.01.2017 10:41+1Если «как угодно» — то это либо классическое дополнение нулями области значений до требуемой размерности, либо какие другие способы дополнения.
В Матлабе много чего наворочено «внутри» — но, как всегда в таких случаях — вы берёте готовое.
И «под капот» вас не пускают.
Кстати, дурацкая идея — я гляжу, что во всех научных расчётах есть тенденция разбивать всё на составляющие — Ez, Ex, Ey и т.д.
А если поступить наоборот?
Ну т.е. у нас фиксируется пространство «точек», в каждой точке имеется набор свойств — запись либо массив, Ex, Ey, Ez, Hx, Hy, Hz — и, возможно — локальные производные.
Тогда локальные расчёты автоматически локализуются ;)) — для двумерного случая у нас будет три «слайса» из массива по три элемента в каждом. Или даже два.
Возможно алгоритм будет работать «компактнее».
opaopa
11.01.2017 17:55В таком случае размер структуры становится некратен ^2 и плохеет префетчеру и кратности размеру строки кэша.
Intel VTune Amplifier в https://habrahabr.ru/company/intel/blog/310842/ предлагает обратно разбить на несколько массивов
aso
12.01.2017 10:56Кхе.
Падами забить до требуемого размера?
(Двумерный случай, кстати — должен быть кратен, трёхмерный придётся добивать до четырёх измерений. %)vlanko
12.01.2017 11:02Думаю, имелось в виду, что массив из 3-6 компонент не кратен 4м.
Но я мог бы сложить в одну матрицу Ez, Hx, Hy, e — как раз 2^2

Gribs
11.01.2017 21:35Кстати про преобразование фурье, в матлаб используется библиотека fftw. Сама библиотека написана на си. Там не совсем «как угодно», производительность возрастает если длина факторизуется на малые простые числа.

aso
12.01.2017 09:38Ну, в принципе, известно, что БПФ предъявляет требования к размеру набора исходных данных.
Наиболе распространённый вариант — Кули-Тьюки — предполагает размер датасета в степень двойки, другие варианты прореживания — хотя-бы факторизуемость.

aso
11.01.2017 11:52Кстати, свести этот метод к методу конечных элементов нельзя?
А то под МКЭ существуют свои пакеты — от коммерческих до бесплатной Salome.

Siemargl
12.01.2017 02:02В общем, я решил задачку.
Посмотрев ассемблерный код на отличном сайте https://godbolt.org, выяснилось, что gcc в 32-битной версии не использует SSE и подобное.
В итоге нужно брать нормальную 64-битную версию и компилировать примерно так
>-O2 -lstdc++ -march=core-avx2 -m64
Для матрицы 4906х1000 у меня результат изменился со 154с на 29.5с, т.е грубо в 5(пять) раз.
Исходник автора.
Siemargl
12.01.2017 02:17Уточнение, для 32-бит просто нужно дополнительно указывать -mfpmath=sse
Т.е так >-lstdc++ -O2 -march=core-avx2 -m32 -o sie32.exe -mfpmath=sse
Это тоже решает проблему
vlanko
12.01.2017 09:59У меня 32-битный gcc 4.92
Включение опции -mfpmath=sse не изменяет ничего.
Полный набор ваших опций увеличивает время на 5%
Если что, мои опции mingw32-g++.exe -Wall -fexceptions -O2 -march=corei7-avx -O3 -std=c++11
Буду пытаться 64-битный компилятор. Под винду сложно найти нормальное.
Siemargl
12.01.2017 11:55http://netassist.dl.sourceforge.net/project/mingw-w64/Toolchains%20targetting%20Win32/Personal%20Builds/mingw-builds/installer/mingw-w64-install.exe
Это загрузчик. Нужно брать вариант с posix-threads. Оба варианта версии 6.2 i686 и x86-64 работают корректно.
-O3 не рекомендую использовать — глючная
vlanko
12.01.2017 11:08Собственно, вы не могли бы выложить готовое приложение, уточнив размер массива (4096*1000 ?)
И добавив в конце FDTDmainFunction
код типаdouble sum = 0; for (i = 0; i < nx+1; i++) { for (j=0; j<ny+1; j++) { sum+=abs(Ez[i][j]); } } cout << " " << sum << " ";
Siemargl
12.01.2017 12:31Не вопрос https://yadi.sk/d/87Kyv5eQ38ZYHf
Там исходник, необходимый рантайм, батник для компиляции под AVX, и две версии — SIMD и обычная O2 — см батникvlanko
12.01.2017 13:01Требует libgcc_s_dw2-1.dll
После установки гсс оно появится?
Siemargl
12.01.2017 13:13Сорри, недоглядел. Перевыложил по той же ссылке
Конечно. Рантайм GCC лежит в папке bin компилятора. К сожалению с ним затруднительно слинковаться статически.
vlanko
12.01.2017 13:55У вас что-то не так с компилятором. Возможно, О3 рулит.
i7-4771
Моя версия выполняется 22,3 секунд
ваша в моем компиляторе 22,4 (конечно, это тоже самое)
Ваш АВХ 23,2
Ваша без инструкций 93,5 секунд
Siemargl
12.01.2017 17:20Все так. Это всего лишь значит, что у вас по умолчанию используется sse математика.
Для этого процессора архитектура -march=haswell
В этом тесте -O3 вроде ничего не ломает.
У меня сейчас i7-4702mq, той же архитектуры.
Итого
gcc (i686-posix-dwarf-rev1, Built by MinGW-W64 project) 6.2.0
gcc.exe aut-res.cpp -lstdc++ -O3 -march=haswell -mfpmath=sse -o aut-avx.exe
4096х1000 результат 22.8с
Java(TM) SE Runtime Environment (build 1.8.0_112-b15)
Java HotSpot(TM) 64-Bit Server VM (build 25.112-b15, mixed mode)
4096х1000 результат Full calculate time 37.323 sec
Компилировалось javac.exe -encoding UTF-8 BasicEx.java
Siemargl
12.01.2017 17:43Потребление памяти 132Мб против 222Мб у Явы.
vlanko
12.01.2017 21:00131 МБайт — это и есть объем массивов двух компонент. А Джава-машина сама жрет много.
Но главное — я проверил gcc 64 6.2 -march=native. На широких задачах (16384 — лучше для 4 ядер) на 35% быстрее старого.
Но VisualStudio еще на 3-10% быстрее.

semio
12.01.2017 13:39for (j = 2; j <= tt; j++) {//можно ли тут оптимизировать порядок доступа к ячейкам?
Можно уменьшить количество обращений к памяти. Примерно так:
final int lastNx = nx - 1; for (int i = 1; i <= lastNx; i++) { double hx0 = Hx[i][1]; double hy0 = Hy[i][1]; double hx, hy; for (int j = 2; j <= tt; j++) { hx = Hx[i][j]; hy = Hy[i][j]; Ez[i][j] += e[i][j] * (hx0 - hx + hy - hy0); hx0 = hx; hy0 = hy; } }
Осталось только посчитать магнитное поле
Аналогично оптимизируется.
co.E[i][j] = co.E[i][j] * co.E[i][j] + si.E[i][j] * si.E[i][j];
Опять избыточные обращения к памяти. Лучше так:
double co = co.E[i][j]; double si = si.E[i][j]; co.E[i][j] = co * co + si * si;
Компилятор может такие вещи оптимизировать. Но всегда полагаться на оптимизатор я бы не советовал.
К тому же:
- Объявления счетчиков циклов (i,j) нельзя выносить за пределы циклов.
- Циклы с условиями вида «i < nx + 1» лучше разворачивать в обратную сторону либо вычислять nx+1 заранее.
- В цикле условия на счетчик типа «j < begin» и «j — begin» следует избегать. Стоит разбить на 2 цикла: до «begin» и после.
- Всё, что выносится за пределы цикла, надо таки вынести. Например: «dx / period», "(t — 1) * dt / tau", "(t — 1) * dt) * omega", "(double) nx / 2 + 0.5" и т.д.
- Где посмотреть полный код на java? Желательно с юнит-тестами… Простор для оптимизации тут явно есть. Ну и параметры запуска надо бы озвучить.

Refridgerator
18.01.2017 13:53Можно ли этот код использовать для расчёта акустических волн?
vlanko
18.01.2017 17:02Акустикой я никогда не занимался. Знаю, что впервые такие сетки использовались в гидродинамике, для векторов давления и скорости.
Нужно смотреть конкретные уравнения. Возможно, в акустике будет проще.
По сути, это уравнения Максвелла — то, что до волн. Если нужны просто волны — там более быстрые методы.


kosmos89
На самом деле списывать надо на то, что вы не специались по распараллеливанию, как и не специалист по оптимизации...
Кстати, у вас в коде на C++ есть несколько new, но ни одного delete...
opaopa
О да, Intel VTune Amplifier спасет отца русской демократии:
https://habrahabr.ru/company/intel/blog/310842/
vlanko
Мне было бы интересно, поможет ли коду Интеловский компилятор, но у меня его нет :)
opaopa
сам компилятор поможет несильно, а такой хороший профайлер покажет много полезного.
vlanko
Да, код делался только под i7. Скорее всего, для Атлона нужно смотреть отдельно.