Задача
В статья использованы возможности пакета SymPy совместно с пакетом NumPy. Всё сводиться к преобразованию символьных выражений в функции способные работать с другими модулями Python.
Процесс решения дифференциальных уравнений становиться наглядным и хорошо контролируемым на каждом этапе вычислений. Следует отметить, что колебательное звено в разных интерпретациях обсуждается в сетях [1,2]. Например, в [3] приводиться модель колебательного звена с подробным исследованием переходных процессов.
Надеюсь, что подобные исследования колебательного звена на Python найдут своих сторонников.
Код программы
Чтобы не утомлять читателя приведу сразу код программы с пояснением каждой значимой строки.
Код
import numpy as np
from sympy import *
from IPython.display import *
import matplotlib.pyplot as plt
init_printing(use_latex=True)
var('t C1 C2')
u = Function("u")(t) # Это переменная, но не функция.
m=20 #Показатель массы.
w=10.0#Показатель демпфирования колебаний.
c=0.3#Показатель жёсткости.
a=1#Бесконечный импульс силы.
#Все показатели условные(только для исследования характера зависимостей).
t#Текущее время.
de = Eq(m*u.diff(t,t)+w*u.diff(t)+c*u,a) #-Дифференциальное уравнение колебаний.
display(de)#-Вывод на дисплей.
des = dsolve(de,u)#Символьное решение уравнения методом Коши в общем виде.
display(des)#Вывод на дисплей.
eq1=des.rhs.subs(t,0);#Условие равенства нулю перемещения в момент времени t=0.
display(eq1)#Вывод на дисплей.
eq2=des.rhs.diff(t).subs(t,0)#Условие равенства нулю скорости перемещения в момент
# времени t=0.
display(eq2)#Вывод на дисплей.
seq=solve([eq1,eq2],C1,C2)#Решение системы для определения коэффициентов C1,C2.
display(seq)#Вывод на дисплей.
rez=des.rhs.subs([(C1,seq[C1]),(C2,seq[C2])])#Вид решения дифференциального
#уравнения с численными значениями коэффициентов.
display(rez)#Вывод на дисплей.
f=lambdify(t, rez, "numpy")#Перевод символьного решения в численное для работы
#с модулем numpy .
x = np.arange(0.0,500,0.01)
plt.plot(x,f(x),color='b', linewidth=3)
plt.xlabel('Time t seconds',fontsize=12)
plt.ylabel('$f(t)$',fontsize=16)
plt.grid(True)
plt.show()
Настроим демпфирование и получим апериодическое движение и все этапы решения уравнения.

Eq(0.3*u(t) + 10.0*Derivative(u(t), t) + 20*Derivative(u(t), t, t), 1)
Eq(u(t), C1*exp(t*(-5 — sqrt(19))/20) + C2*exp(t*(-5 + sqrt(19))/20) + 3.33333333333333)
C1 + C2 + 3.33333333333333
C1*(-1/4 — sqrt(19)/20) + C2*(-1/4 + sqrt(19)/20)
{C1: 0.245131115588015, C2: -3.57846444892135}
0.245131115588015*exp(t*(-5 — sqrt(19))/20) — 3.57846444892135*exp(t*(-5 + sqrt(19))/20) + 3.33333333333333
Изменим параметры и перепишем листинг программы для отображения трёх движений с возрастающим демпфированием на одном графике.
Код программы для трех различных значений показателя демпфирования
import numpy as np
from sympy import *
from IPython.display import *
import matplotlib.pyplot as plt
init_printing(use_latex=True)
var('t C1 C2')
u = Function("u")(t) # Это переменная, но не функция.
m=200 #Показатель массы.
w=1.8#Показатель демпфирования колебаний.
c=1.3#Показатель жёсткости.
a=1#Бесконечный импульс силы.
#Все показатели условные (только для исследования характера зависимостей).
t#Текущее время.
man=[0.8,2.12,5]#Список условных значений демпфирования (только для построения графиков).
for w in man:
de = Eq(m*u.diff(t,t)+w*u.diff(t)+c*u,a) #-Дифференциальное уравнение колебаний.
display(de)#-Вывод на дисплей.
des = dsolve(de,u)#Символьное решение уравнения методом Коши в общем виде.
display(des)#Вывод на дисплей.
eq1=des.rhs.subs(t,0);#Условие равенства нулю перемещения в момент времени t=0.
display(eq1)#Вывод на дисплей.
eq2=des.rhs.diff(t).subs(t,0)#Условие равенства нулю скорости перемещения в момент времени t=0.
display(eq2)#Вывод на дисплей.
seq=solve([eq1,eq2],C1,C2)#Решение системы для определения коэффициентов C1,C2.
display(seq)#Вывод на дисплей.
rez=des.rhs.subs([(C1,seq[C1]),(C2,seq[C2])])#Вид решения дифференциального уравнения
#с численными значениями коэффициентов.
display(rez)#Вывод на дисплей.
f=lambdify(t, rez, "numpy")#Перевод символьного решения в численное для работы с модулем numpy .
x = np.arange(0.0,500,0.01)
if w==man[0]:#Три перемещения на одном графике.
plt.plot(x,f(x),color='r', linewidth=3)
elif w==man[1]:
plt.plot(x,f(x),color='g', linewidth=3)
elif w==man[2]:
plt.plot(x,f(x),color='b', linewidth=3)
plt.xlabel('Time t seconds',fontsize=12)
plt.ylabel('$f(t)$',fontsize=16)
plt.grid(True)
plt.show()
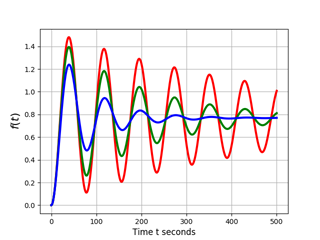
Установим значение параметра демпфирования и получим график периодического затухающего движения и все этапы решения трех уравнений.
Eq(1.3*u(t) + 0.8*Derivative(u(t), t) + 200*Derivative(u(t), t, t), 1)
Eq(u(t), (C1*sin(sqrt(406)*t/250) + C2*cos(sqrt(406)*t/250))/exp(t)**(1/500) + 0.769230769230769)
C2 + 0.769230769230769
sqrt(406)*C1/250 — C2/500
{C2: -0.769230769230769, C1: -0.0190881410379025}
(-0.0190881410379025*sin(sqrt(406)*t/250) — 0.769230769230769*cos(sqrt(406)*t/250))/exp(t)**(1/500) + 0.769230769230769
Eq(1.3*u(t) + 2.12*Derivative(u(t), t) + 200*Derivative(u(t), t, t), 1)
Eq(u(t), (C1*sin(sqrt(647191)*t/10000) + C2*cos(sqrt(647191)*t/10000))/exp(t)**(53/10000) + 0.769230769230769)
C2 + 0.769230769230769
sqrt(647191)*C1/10000 — 53*C2/10000
{C2: -0.769230769230769, C1: -0.0506776284001243}
(-0.0506776284001243*sin(sqrt(647191)*t/10000) — 0.769230769230769*cos(sqrt(647191)*t/10000))/exp(t)**(53/10000) + 0.769230769230769
Eq(1.3*u(t) + 5*Derivative(u(t), t) + 200*Derivative(u(t), t, t), 1)
Eq(u(t), (C1*sin(sqrt(1015)*t/400) + C2*cos(sqrt(1015)*t/400))/exp(t)**(1/80) + 0.769230769230769)
C2 + 0.769230769230769
sqrt(1015)*C1/400 — C2/80
{C2: -0.769230769230769, C1: -0.120724003956605}
(-0.120724003956605*sin(sqrt(1015)*t/400) — 0.769230769230769*cos(sqrt(1015)*t/400))/exp(t)**(1/80) + 0.769230769230769
Уменьшим показатель массы и получим графики движения (решение уравнений для сокращения упускаем).

Рассмотрим важный случай отрицательного демпфирования и получим соответствующий график (решение уравнений для сокращения упускаем).
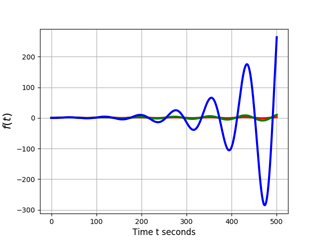
Вывод
Полученная графическая иллюстрация работы колебательного звена полностью соответствует теории.
Символьное и численное решений дифференциального уравнения на SymPy и NumPy позволило создать адекватную модель колебательного звена с управление массой демпфированием и жёсткостью и при этом контролировать ход ращения уравнения колебаний. Кроме этого Python условно бесплатное программное обеспечение, что значительно расширяет возможности применение приведенной программы в исследовательских и учебных целях.
Ccылки
Поделиться с друзьями
Комментарии (5)

saluev
04.04.2017 16:31+4Почему вы не оформите формулы в LaTeX? SymPy, кстати, тоже вроде умеет экспортировать для латеха.
ivlis
04.04.2017 22:52+8> Процесс решения дифференциальных уравнений становиться наглядным и хорошо контролируемым на каждом этапе вычислений
А вот статье и не скажешь, ничего не наглядно. Даже понять какую задачу человек решает невозможно.
windgrace
06.04.2017 11:05+2Полученная графическая иллюстрация работы колебательного звена полностью соответствует теории.
Почему? И какой теории? А в каком смысле соответствует? Графики визуально похожи? Или есть какая-то метрика? А что мы вообще решаем?
Хотя бы общую постановку задачи надо было описать — а то статья превращается в «вот код, он работает и, поверьте мне, работает правильно».


Meklon
Пригодится, спасибо. Правда стиль подачи какой-то очень формальный, словно копипаста из научной работы.