Привет, меня зовут Иван Греков, я работаю во фронтенд-команде Badoo, занимаюсь вёрсткой пользовательских интерфейсов на проектах компании.

В работе с макетами интерфейсов я использую графические редакторы, такие как Adobe Photoshop и Sketch. В них все слои по умолчанию представляют собой прямоугольные контейнеры. Когда мы выравниванием один слой по центру относительно другого, то для выравнивания используются центры прямоугольных контейнеров. Такой подход крайне неудобен при работе с иконками, поскольку выравниваемые фигуры могут сильно отличаться от прямоугольных контейнеров. И чем больше несимметричная фигура отличается по площади и по точкам координат от прямоугольника, в границы которого она вписана, тем заметнее разница между центрами фигуры и её контейнера. Это приводит к дисбалансу композиции в интерфейсных иконках.

Такая ситуация хорошо знакома специалистам в области дизайна, обычно она решается вручную, что требует определённых знаний и навыков. Именно поэтому она может создавать трудности для верстальщиков и разработчиков, которые решают эту задачу подручными инструментами.

Приведу пример. Сделаем в графическом редакторе иконку – алмаз, вписанный в круг. На иллюстрации видно, что нижняя часть алмаза уступает по размеру верхней. Создаётся впечатление, что алмаз смещён вверх относительно центра изображения, хотя это не так.

Это и есть дисбаланс, о котором я говорил выше. Он становится заметен на этапе вёрстки элементов пользовательских интерфейсов. Чтобы выявить проблему заранее, при приёмке дизайна и при оценке качества макетов необходимо обратить внимание на то, насколько визуально выровнены фигуры в иконках. Если внутри иконок они не выглядят сбалансировано (как в нашем примере), им потребуется оптическая компенсация.

Оптическая компенсация – это расстояние, на которое следует сдвинуть фигуру для достижения визуального баланса относительно других слоёв. Для этого мы меняем координаты центра контейнера так, чтобы они соответствовали координатам центра фигуры, а затем выравниванием фигуру относительно нового центра.

Поиск координат центра фигуры и последующее выравнивание слоёв в этом посте я буду называть оптическим выравниванием. Этот термин используется графическими дизайнерами для обозначения балансировки размера букв и расстояний между ними в шрифтах. Однако в статьях на «Медиуме» (статья 1 и статья 2) упоминается, что этот способ подходит для выравнивания фигур внутри группы слоёв.

Оптическое выравнивание может делаться и «на глаз»: это под силу дизайнерам с большим опытом и развитым чувством баланса. В этом подходе нет строгих критериев по допустимым расстояниям и габаритам фигур: дизайнер самостоятельно определяет, на сколько процентов следует сдвинуть фигуру или изменить её размер для достижения оптического баланса на экране. Но такой подход часто приводит к субъективизму: мнение дизайнера может не совпадать с мнением пользователей или заказчика. Как определить, что в одном случае изображение визуально выровнено, и это не должно вызывать сомнений, а в другом – центр фигуры имеет погрешность в 5–10%, возникшую из-за работы «на глаз», и внутри иконки наблюдается смещение? В графическом дизайне сетка, расстояния, выравнивание и отступы определяются брендбуком или гайдлайном, в которых описываются стилистика проекта и элементы дизайна. Это помогает при разрешении споров о выравнивании элементов. Для пользовательских интерфейсов подобные решения, увы, не являются повсеместной практикой.

Если у проекта нет документации для пользовательских интерфейсов, дизайн-системы не применяются, то выравнивание – это ответственность дизайнеров. Верстальщикам и разработчикам важно обсуждать такие вопросы с дизайнерами. Однако не всегда это можно сделать, по разным причинам: сроки проекта уже обозначены, времени на редизайн нет, дизайнеры загружены другими задачами, проект дизайна был сделан на аутсорсе и так далее. Я встречал немало ситуаций с такими вводными: предоставлен «готовый» дизайн в файле, и его нужно реализовать хорошо и быстро. В этом ключе мы и поговорим о том, что следует знать об оптическом выравнивании иконок верстальщикам и разработчикам, чтобы задачи по разработке новых пользовательских интерфейсов выполнялись качественно и без потери скорости разработки.

Для начала попробуем разобраться в существующих решениях. Ознакомимся с тем, что писали об оптическом выравнивании ранее. В 2015 году на Хабре опубликовали перевод одной из двух ранее упомянутых статей с «Медиума» (статья 1). Там приводились примеры простых иконок и предлагалось выравнивать их слои двумя способами: вписывая фигуру в круг или поворачивая её вокруг своей оси. Основное преимущество этих способов – простота применения. И я решил попробовать – благо на разных проектах существует не менее ста вариаций различных иконок.

Инструкция по оптическому выравниванию

Что общего у выравнивания иконок методами, указанными выше, и у процесса рисования совы? То, что самое интересное в обоих случаях остаётся «за кадром». Если говорить про иконки, то при автоматическом выравнивании вне фокуса оказывается вопрос определения центра фигуры. В переводных статьях часто упоминается о том, что позиционирование фигур выполняется «вручную» на усмотрение читателя.

По умолчанию центр слоя с фигурой задан заранее в виде центральной точки прямоугольного контейнера, содержащего фигуру. Такой подход не предусматривает возможности для поиска центра фигуры. И если координаты центра контейнера определяются автоматически, то координаты центра фигуры можно найти через оптическое выравнивание. Мы находим центр фигуры и относительного него проводим выравнивание.

Если попробовать составить инструкцию, то для применения оптического выравнивания в ежедневной работе потребуется совершить всего три простых шага:

• определяем, какой формы фигура перед нами;
• находим центр фигуры;
• выполняем выравнивание.

Подход незначительно отличается для простых и составных фигур на втором шаге.

Итак, на первом этапе нам нужно определить тип каждой фигуры. Попробуем детально разобрать шаги, чтобы после первого применения у разработчика сразу возникло понимание, как работает оптическое выравнивание.

Простая фигура.

Шаг 1

Графический редактор изначально определяет центр любой фигуры как центр её прямоугольного контейнера. Это предпосылка для понимания того, что за фигура перед нами. Когда мы имеем дело с относительно простой фигурой, её центр можно найти по специальной форме определения барицентра. Существуют отдельные формулы для треугольников, параллелепипедов и других несоставных фигур; они помогают найти точку, относительно которой надо центрировать иконки.

Вписываем фигуру в границы круга, и его центр можно выровнять относительно контейнера. Такой подход отлично работает, если у фигуры присутствует симметрия хотя бы в одной плоскости.

Разберём пример с иконкой воспроизведения видео. Она достаточно примитивна и часто является характерным примером оптического дисбаланса. Попробуем воспроизвести такую ситуацию: открываем любой графический редактор, создаём треугольник и круг. А теперь пробуем выровнять две фигуры автоматически. Посмотрим, что получилось:

В иконке что-то определённо не так. Давайте попробуем разобраться, в чём причина оптического дисбаланса:

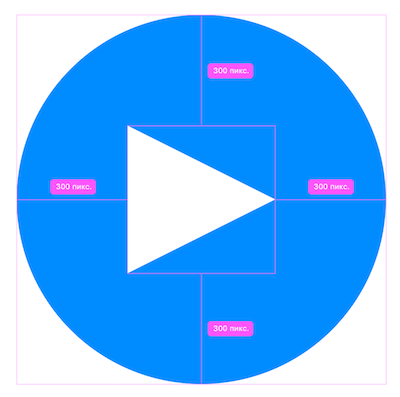
Простая фигура. Шаг 2

На иллюстрации видно, что на левом круге треугольник равномерно вписан в прямоугольник, а точнее – в квадрат. Геометрический центр треугольника не совпадает с центром его квадратного слоя.

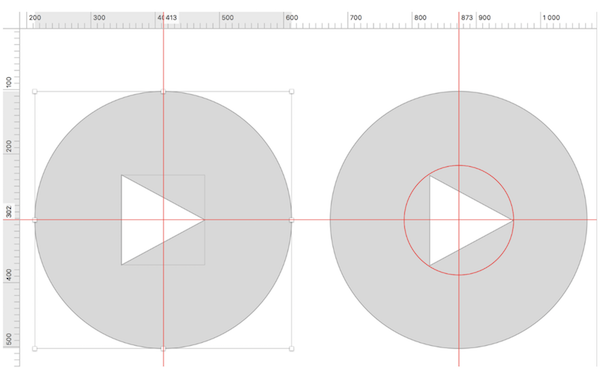
Исправим это: добавим третью фигуру – круг, как в иллюстрации справа. В этот круг впишем треугольник и сгруппируем их. Затем эту группу элементов необходимо выровнять относительно фонового круга.

Проверяем расположение фигур:

Сейчас фигуры оптически выровнены относительно друг друга. Попробуем сравнить иконки, убрав круговой контейнер для наглядности:

Правая иконка выглядит аккуратно, так как она оптически выровнена. Мы получили быстрое решение проблемы для простых фигур.

Сложная фигура.

Шаг 1

Если перед нами фигура сложная (например, составная), для её выравнивания нужно выполнить ещё одно действие. Применение такого подхода требуется при работе с фигурами без выраженной симметрии, такими как логотипы компаний или социальных сетей.

Попробуем разобраться на примере иконки приложения Hot or Not.

Для сложной фигуры нужно определить необходимый минимальный радиус круга (он должен полностью содержать все детали выравниваемой фигуры). Как и при работе с простой фигурой, сначала мы вписываем фигуру в круговой контейнер. Затем для сложной фигуры определяется необходимый радиус при помощи поворота фигуры вокруг своей оси относительно её центра.

При повороте фигура не должна выходить за границы круга. Как только это происходит, необходимо увеличить радиус круга. Круговой контейнер таких фигур всегда больше, чем у простых фигур примерно той же площади.

Сложная фигура. Шаг 2

На втором шаге мы выравниваем круговой контейнер фигуры относительно элемента-«родителя». Теперь иконка должна быть выровнена, давайте убедимся в этом:

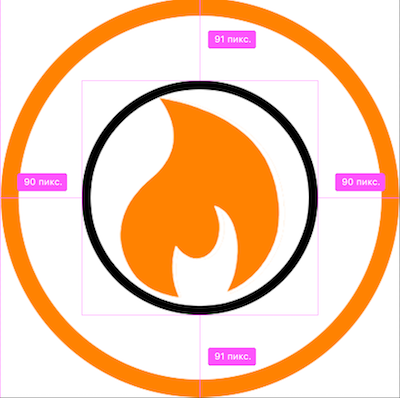
Внутри каждого контейнера фигура находится в центре, на одном расстоянии от границ контейнера. Это хороший способ проверить выравнивание сложных иконок.

При работе с определёнными иконками эти способы позволяют выравнивать фигуры достаточно быстро и эффективно. Однако, проверяя их на примере большого количества иконок для десктопной версии сайта Badoo, я обнаружил вот что:

• в статьях не указаны критерии для определения метода поиска центра для разных фигур (какой метод идеально подойдёт для треугольника, а какой – для полигонного логотипа?);
• эти методы указывают разные координаты, и впоследствии проверка делается «на глаз»;
• отсутствуют описания, как перечисленные в статьях методы работают (они работают, но не для всех иконок);
• нет чёткого списка фигур и их признаков, для которых работает любой из описанных методов оптического выравнивания (в некоторых случаях оба метода не подойдут).

Маловероятно, что в качестве иконки для интерфейса кто-то будет использовать вписанный в круг конус или полигон без определённой смысловой нагрузки. Но всё же хотелось бы понимать, как сделать так, чтобы разные иконки были выровнены, и это не вызывало сомнений. Указанные выше способы не являются панацеей и требуют временных затрат, если вы не являетесь гуру в области графического дизайна. Попробуем применить один из способов, чтобы проиллюстрировать все вышесказанное.

Продолжим пример с иконкой алмаза. Ниже представлены два варианта выравнивания внутри иконки: фигура слева вписана в прямоугольник, фигура справа вписана в окружность, оба контейнера выровнены по центру относительно фиолетового круга.

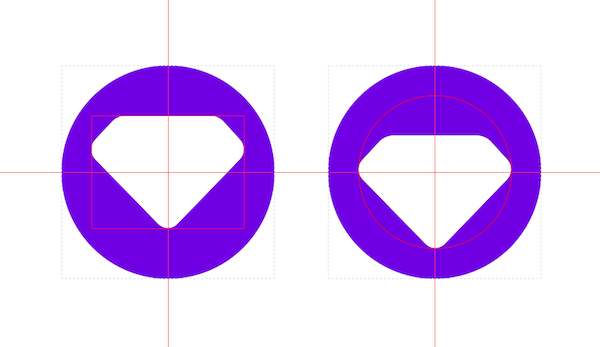
Как видно, оба варианта далеки от решения задачи по выравниванию фигур по центру. Левую иконку хочется расположить ниже, а правую – выше. Получается, что подход с кругом здесь неоптимален. Также я пробовал подход с вращением иконки, и он дал третий результат. Во всех трёх случаях потребуется использовать дополнительные действия по оптической компенсации, и делать это придётся «на глаз».

Но далеко не все обладают врождённым чувством вертикального ритма и ощущением золотого сечения; значит, вместо выравнивания «на глаз» необходимо исходить из универсального, максимального абстрактного алгоритма, позволяющего находить центр любой фигуры. В идеале такой процесс оптического выравнивания следует автоматизировать. Но чтобы автоматизировать процесс, необходимо его понимать. Поэтому я решил выйти за границы графического дизайна и изучил существующие решения и теорию, чтобы выполнять оптическое выравнивание с минимальными затратами времени и сил.

Немного теории

Оптическое выравнивание иконок я рассматриваю как решение из области геометрии. Для выравнивания необходимо найти центральную точку геометрической фигуры. В геометрии это называется задачей по поиску барицентра, геометрического центра фигуры или centroid в англоязычных источниках. В «Википедии» пишут, что в физике и геометрии барицентр представляет собой точку пересечения медиан. Он выступает в роли геометрического центра любой двумерной области.

Барицентр можно представить как среднее арифметическое положений всех точек фигуры. Центр масс, центр тяжести, барицентр для нас будут считаться одной точкой фигуры. Такое допущение возможно, так как мы работаем с пользовательскими интерфейсами. Если мы будем искать центр модели 3D-объекта или центр географического периметра через определение барицентра, то нам нужно будет разделить вышеперечисленные понятия и добавить много исключений из общих правил. Но в этом посте речь идёт только об оптическом выравнивании иконок пользовательских интерфейсов.

Определение барицентра распространяется на любой объект в n-мерном пространстве – барицентр является средним положением всех точек фигуры по всем координатным направлениям. Грубо говоря, это точка равновесия фигуры. Для пользовательских интерфейсов имеет значение тот факт, что с помощью формулы определения барицентра можно найти правильную точку для выравнивания фигур.

Поиск барицентра начинается с определения того, какая фигура перед нами. Для ряда иконок задача тривиальна:

• барицентр квадрата, прямоугольника и параллелограмма находится в точке пересечения диагоналей, и графические редакторы при работе с этими фигурами по умолчанию выставляют правильные координаты, оптическое выравнивание не требуется;
• барицентр круга, кольца и шестиугольника расположен в точке центра этих фигур, графические редакторы опять же справляются с выравниванием слоёв;
• барицентр эллипса лежит в точке пересечения осей, автоматическое выравнивание также работает корректно.

Вывод: если иконка имеет центр симметрии, то её барицентр совпадает с центром симметрии. На иллюстрации ниже круг и квадрат имеют один барицентр. А карандаш – нет.

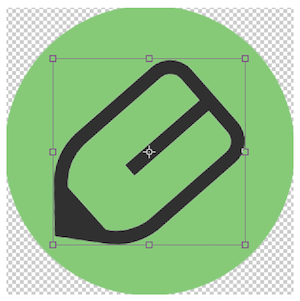
Для многих фигур, таких как фигура карандаша, требуется выполнить дополнительные вычисления:

• барицентр треугольника лежит в точке пересечения медиан (треугольники бывают разные, поэтому необходимо применять оптическое выравнивание после вычисления барицентра;
• барицентр полукруга определяется по формуле (4 Radius) / 3 ?. (относительно этой точки мы можем применить оптическую компенсацию к фигуре);
• барицентр трапеции лежит на прямой, соединяющей центры оснований.

Барицентры более сложных или составных фигур требуют дополнительных вычислений. Например, если фигура может быть поделена на равные части, как алмаз в примерах выше, то для неё действуют следующее правило поиска барицентра:

• если иконка имеет ось симметрии, то её центр тяжести лежит на этой оси.

Список формул для разных фигур можно посмотреть на страничке в «Википедии» (она немного отличается на русском и на английском).

Так мы можем определить степень выравнивания фигуры по одной из осей. Это практически половина дела. Но что делать, если фигура несимметрична?

Разберём три способа поиска барицентра, применимых для большинства фигур вне зависимости от симметрии: метод геометрического разложения, метод интегрирования и поиск барицентра для конечного множества точек.

В первом способе мы разбиваем сложную фигуру на более простые формы, а затем применяем эту формулу для поиска координат:

где координаты барицентров простых фигур обозначаются Gi (соответственно для осей X и Y), а площади фигур обозначаются Ai.

Однако, так как мы используем графические редакторы и планируем автоматизировать решение этой задачи, мы можем отказаться от разбиения фигуры на примитивы, не учитывать симметрию и вычислять барицентр фигуры. Для этого можно применить метод интегрирования:

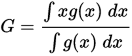
В этом случае g является характеристической функцией подмножества, принимающей 1 внутри X и 0 вне его. Из этой формулы получаем координаты по осям X и Y:

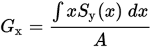
Мы можем ещё больше упростить задачу для автоматизации, так как мы всегда знаем координаты точек фигуры для выравнивания и их количество. Находим координаты геометрического центра фигуры следующим способом: каждая координата центра представляет собой сумму всех величин, поделённую на количество координат фигуры по этой оси (этот подход наиболее удобен для автоматизации). На этом этапе появляется основа для процесса автоматизации оптического выравнивания и для создания технического решения. Для нерегулярного применения можно ограничиться методом оптического выравнивания «на глаз». Однако, когда приходится иметь дело с большими объёмами иконок и элементов пользовательского интерфейса, имеет смысл задуматься об автоматизации.

Автоматизируем это

Изучая решения на просторах интернета, я обнаружил решение для Adobe Illustrator CS3 на базе JavaScript:

/*
JET_Centroid.jsx
A Javascript for Adobe Illustrator CS3.
Purpose: Finds the centroid (center of gravity) of selected triangles and other straight-sided multigon paths and draws a user-defined circle at that location.
To Use: Make a selection which includes normal paths. Call the script.
*/
var docRef = activeDocument;
var markerSize = prompt("How large (in points) do you want the centroid marker to be?", 6);

for(s = 0; s < docRef.selection.length; s++){
    if(docRef.selection[s].typename == "PathItem"){
        var currPath = docRef.selection[s];
        var xTotal = 0;
        var yTotal = 0;
        for (p = 0; p < currPath.pathPoints.length; p++){
            var currPoint = currPath.pathPoints[p];
            xTotal += currPoint.anchor[0];
            yTotal += currPoint.anchor[1];
        } //end if for loop
        var centroidX = xTotal / currPath.pathPoints.length;
        var centroidY = yTotal / currPath.pathPoints.length;
        var marker = docRef.pathItems.ellipse(centroidY + (markerSize / 2),centroidX - (markerSize / 2), markerSize, markerSize, 0, 0);
        marker.strokeColor = docRef.swatches.getByName("Black").color;
        marker.filled = false;
    }//end if
}//end for loop

Изучив решение, я решил доработать его под Adobe Photoshop – и получилась такая последовательность шагов по определению геометрического центра:

1. В Photoshop выравниваем фигуры по центру автоматически.
2. Выделяем в палитре слоёв слой с кривыми (Path).
3. Открываем меню «Сценарии».
4. Выбираем «Обзор».
5. Запускаем GetCentroid.jsx.
6. Точка пересечения двух направляющих является ориентиром для выравнивания, поверх её координат следует расположить центр фигуры.

Скрипт «под капотом» выполняет следующие шаги:

1. Сбрасывает все координаты в пиксели.
2. Находит выделенные слои, содержащие кривые.
3. На каждом слое, в каждой кривой собираются координаты точек, чтобы создать на каждую кривую свой объект с координатами.
4. Находит площадь для каждого объекта.
5. Находит координаты центроида для каждого объекта.
6. В качестве значений для направляющих применяет разницу между шириной страницы и значением по оси X, высотой и значением по оси Y.
7. Строит направляющие инверсивно для каждой оси координат.

Это позволяет оценить требуемый объём оптической компенсации перед выравниванием.

Пример выравнивания с помощью скрипта.

C кодом скрипта можно ознакомится (и скачать) в моём репозитории на GitHub.

Подобный скрипт можно применять и в других программах. JS-библиотека D3 уже содержит такой механизм. Это означает, что при желании можно внедрить аналогичную процедуру в систему сборки или в дизайн-систему компании. Или воспользоваться плагином для Sketch. Или написать свой собственный. Необязательно применять ручное решение для выравнивания всех иконок на проекте. Существуют плагины и решения для графических редакторов, например, платный плагин Optically для Sketch.

Если вы ещё не применяете подобные решения по оптическому выравниванию в своей работе, имеет смысл присмотреться к разрабатываемым пользовательским интерфейсам: скорее всего, потребуется поправить выравнивание некоторых их элементов.

Когда применять оптическое выравнивание?

Ответ на этот вопрос зависит от организации работы. Если есть возможность, можно отдать это на откуп дизайнерам. В теории такое возможно, но на практике дизайн следует проверять и на этапах разработки и вёрстки, так как элементы пользовательского интерфейса могут потребовать корректировок.

В Badoo при подготовке иконок для пользовательских интерфейсов все изображения предварительно оптимизируются: линии в SVG объединяются в единый Path, а он выравнивается относительно контейнера. Часть этих действий автоматизирована. Разработчик выравнивает фигуры с помощью графического редактора. При работе с некоторыми иконками это может приводить к смещению центров фигур относительно друг друга. На этом этапе и следует применять оптическое выравнивание, чтобы избежать искажений изображения.

Практика применения и особенности

В пользовательских интерфейсах Badoo используется много различных иконок: иконки действий, статусов и настроек. И часто они ставятся в ряд, поэтому важно, чтобы все они были выровнены. Применяя оптическое выравнивание, мы повышаем качество пользовательских интерфейсов с сохранением темпов вёрстки и разработки.

Оптическое выравнивание позволяет соблюдать баланс внутри композиции для отдельных иконок, рядов иконок одного типа и одного размера. Допустим, у нас три иконки расположены в ряд. Когда у них одинаковый фон, размер и выравнивание фигур внутри, они будут смотреться гармонично. Оптическое выравнивание поможет исправить недочёты дизайна, но не является панацеей при нарушении базовых правил UI-дизайна – это уже совсем другая история, которая прорабатывается исключительно дизайнерами (речь о нарушении вертикальных ритмов страницы и отдельных блоков, качестве изображений и т. д.).

Что касается оптического выравнивания, то существуют определённые ограничения и сложности, с которыми можно столкнуться.

Например, сглаживание иконок в разных браузерах. SVG-иконки содержат векторную графику, координаты точек и другую информацию о фигурах и слоях. В Badoo мы создаём иконки с определёнными размерами холста в зависимости от типа – 16 или 22 пикселя. Если фигура внутри такой иконки содержит точки с нечётными координатами, то при выравнивании по центру будет заметна потеря в резкости SVG-изображения. В таком случае допускаются правки размеров иконки и её элементов.

Кроме того, есть особенности при использовании оптического выравнивания:

• тонкие или выносные элементы фигуры в определённых условиях не влияют на центрирование изображения (эта ситуация, как правило, обрабатывается скриптом);
• разные фигуры одного цвета, расположенные рядом, будут казаться разного оттенка на экране монитора;
• фигуры одного цвета и с одинаковой шириной/ высотой, но разной формы будут казаться не выровненными относительно друг друга. Например, любой круг будет визуально казаться меньше рядом с квадратом такого же размера, поэтому окружность необходимо увеличить в размере.

Первое ограничение разработчик может обойти самостоятельно. Остальные вопросы лежат в области компетенций дизайнера, однако разработчику при работе с пользовательскими интерфейсами также стоит уделять внимание этим моментам – это позволит избежать дополнительной нагрузки в дальнейшем при работе над внедрением новых дизайнов интерфейса.

Выравнивание иконок относительно других элементов на странице часто воспринимается как ограничение. Допустим, иконка является однослойной, выровненной относительно своего контейнера. Мы вставляем её на страницу, где может быть любой контекст и окружающие элементы с различной высотой и выравниванием. Так быть не должно.

В большинстве случаев размещению элементов предшествует дизайн пользовательского интерфейса, где указано положение объектов, выполнено визуальное выравнивание и соблюдён вертикальный ритм элементов. Подготовка полноценного дизайна страниц поможет избежать таких вопросов и неточностей при разработке пользовательских интерфейсов: разработчик получает чёткое представление о контексте расположения элементов на странице и их отображении, и ему просто необходимо следовать утверждённому дизайну.

Почему этот замечание важно для оптического выравнивания иконок? Во многих компаниях есть библиотеки элементов. Библиотека элементов представляет собой отдельные детали пользовательских интерфейсов вне контекста страниц, её наличие позволяет ускорить разработку при использовании её элементов в верстке. Однако, когда новые дизайны страниц или прототипы дизайна не учитывают размерных сеток, позиционирования элементов библиотеки, это преимущество перестаёт работать. Поэтому важно, чтобы в работе с дизайном и библиотекой элементов присутствовал системный подход:

1. На основе первичного дизайна создаётся библиотека элементов с информацией о размерах и вариациях элементов пользовательских интерфейсов.
2. Последующий дизайн страниц отталкивается от библиотеки элементов.
3. Выравнивание в дизайне и размеры строк не должны противоречить существующим в библиотеке элементов вариантам (в противном случае следует внести коррективы в библиотеку).
4. Вёрстка иконок и пользовательских интерфейсов должна соответствовать дизайну и библиотеке элементов.

Как правильно применять оптическое выравнивание в работе?

Оптическое выравнивание помогает исправить недочёты пользовательских интерфейсов вне зависимости от того, была ли ошибка допущена в дизайне или в вёрстке. Этот метод выступает в роли лакмусовой бумажки для пользовательских интерфейсов: он позволяет оценить на практике, как проведена работа с иконками. На него стоит обращать внимание как в процессе дизайна и вёрстки, так и в процессе оценки реализации готового пользовательского интерфейса.

Когда коллеги в общих чертах рассказали мне об этом подходе, я стал активно использовать их рекомендации в работе. Для применения оптического выравнивания важно понимание принципов его работы. Об этом я могу судить по разным проектам, с которыми я работал до прихода в Badoo: не все верстальщики и разработчики придерживаются подхода Pixel Perfect при создании шаблонов и сверяют готовый шаблон с дизайном. Поэтому, когда работаешь в команде, важно договориться с её участниками о единстве применяемых подходов, а новым членам команды необходимо рассказывать о них простым и понятным языком.

Вместо заключения

Хороший пользовательский интерфейс является результатом работы каждого специалиста команды. Он создаётся в процессе выстраивания визуальной гармонии элементов на экране пользователя. Такая гармония может достигаться применением междисциплинарных знаний и навыков. Например, грамотным применением подходов и методов геометрии в дизайне и разработке. В нашем случае таким подходом является оптическое выравнивание – оно помогает повысить качество пользовательских интерфейсов на выходе.

P. S. Внимательный читатель заметит, что иконка в форме алмаза всё ещё остается невыровненной. Любопытно, но это одна из тех форм, которую сложно выровнять, используя геометрические формулы. Но всегда можно обратиться к коллегам-дизайнерам и прийти к консенсусу.

P.P.S. Если сделать углы алмаза острыми, то скрипт для выравнивания показывает хороший результат.