Перевод поста Майкла Тротта (Michael Trott) "Making Formulas… for Everything—From Pi to the Pink Panther to Sir Isaac Newton".
Выражаю благодарность за помощь в переводе Сильвии Торосян.
Скачать перевод в виде документа Mathematica, который содержит весь код использованный в статье, можно здесь (архив, ~7 МБ).

В компании Wolfram Research и Wolfram|Alpha мы любим математику и вычисления. Наши любимые темы — алгоритмы, следующие из формул и уравнений. Например, Mathematica может вычислить миллионы интегралов (точнее бесконечное их количество, встречающихся на практике), а также Wolfram|Alpha знает сотни тысяч математических формул (от формулы Эйлера и BBP-формул для Pi до сложных определённых интегралов, содержащих sin (x)) и множество формул физики (например, от закона Пуазейля до классических решений механики для точечной частицы в прямоугольнике или потенциала обратного расстояния в четырехмерном пространстве, в гиперсферических координатах), так же как менее известные формулы, такие как формулы для частоты дрожащей мокрой собаки, максимальной высоты песочного замка, или времени приготовления индейки.

Недавно мы добавили формулы для множества разнообразных фигур и объектов. В Блоге Wolfram|Alpha были показаны некоторые примеры формирования фигур, которые были задавались с помощью математических уравнений и неравенств. Среди построенных кривых есть кривые образов вымышленных персонажей:





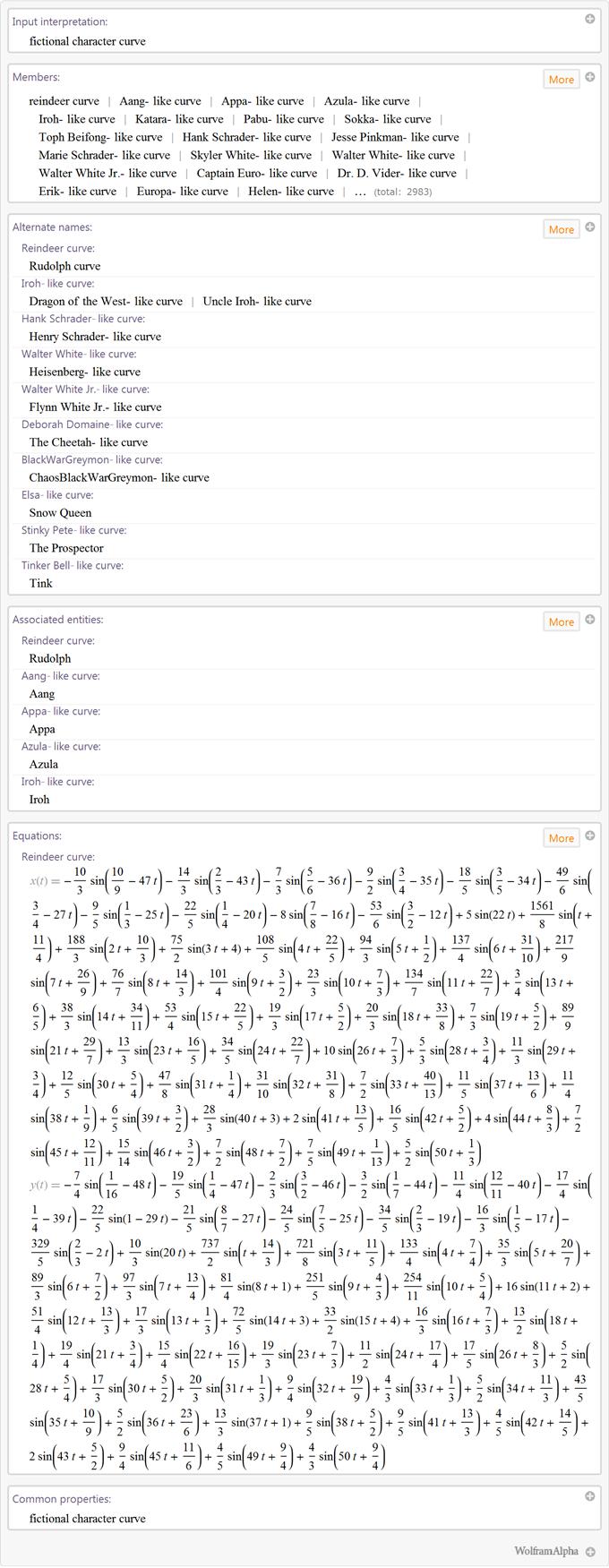
Кривые очертаний объектов:





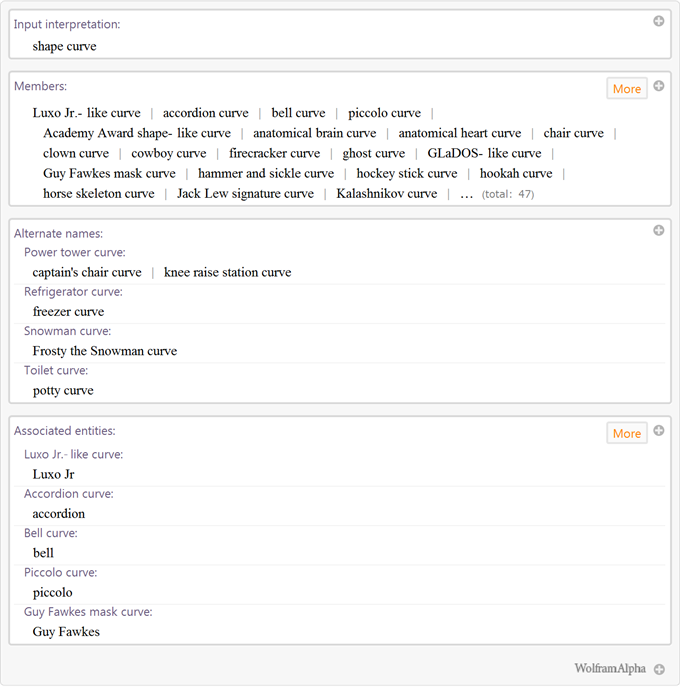
и, наиболее популярные среди наших пользователей, кривые образов реальных людей:





Так как эти кривые в математическом смысле, сходны с лемнискатой или листом Декарта, они более интересны с точки зрения их графического отображения, чем своими математическими свойствами.

После того как, была опубликована статья в блоге Ричарда, мой коллега спросил меня, “Как Вы составляете уравнение, описывающее лицо Стивена Вольфрама?” После минутного размышления над этим вопросом, я понял, что действительно поразительно, вопрос не в том, что существует аналитическое выражение: цифровое изображение (предположим для простоты, что оно черно-белое) представляет собой прямоугольный массив значений серого цвета. По такому массиву можно построить интерполирующую функцию, даже полином. Но такая явная функция была бы очень громадной, длиной в сотни страниц, и не была бы пригодна для какого-либо практического применения. На самом деле трудностью является то, как можно получить аналитическое выражение, которое имело бы сходство с лицом человека, так чтобы оно поместилось на одной странице и имело простую структуру. Аналитическое выражение для кривой, которая изображает лицо Стивена Вольфрама, длиной приблизительно в одну страницу, что сравнимо с размером сложной формулы физики, такой как, скажем, гравитационный потенциал куба.





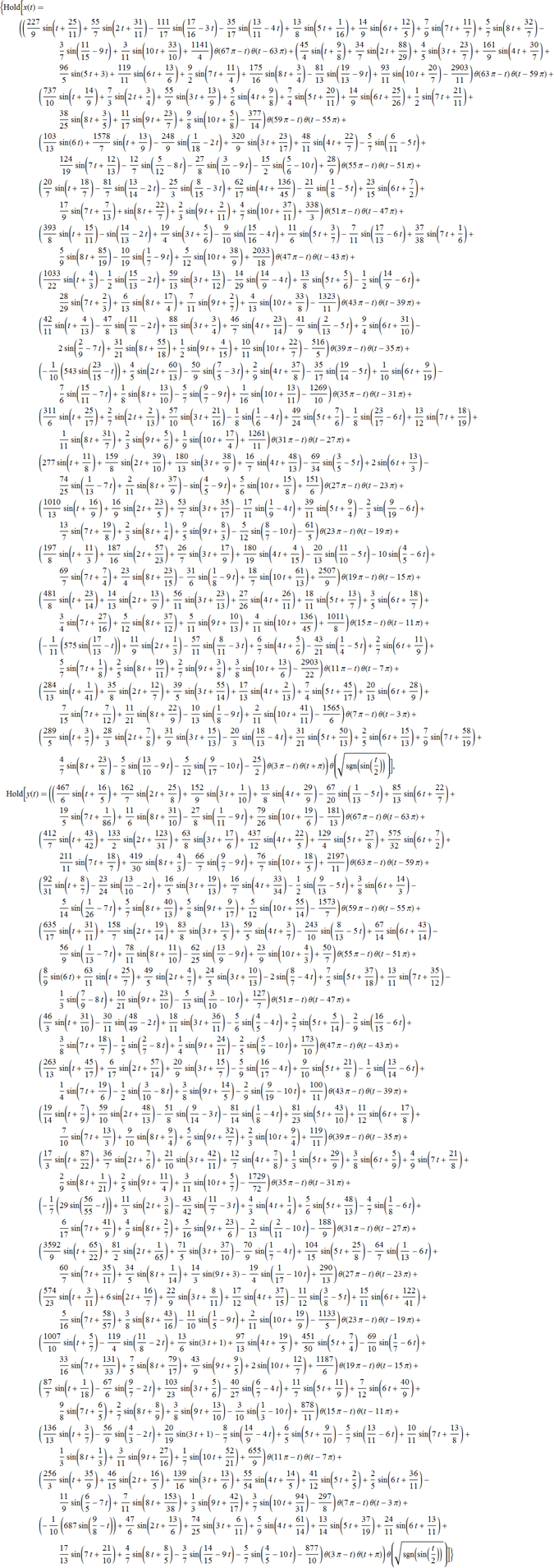
В этой статье я хочу показать, как сгенерировать такого рода уравнения. Совершенно не удивительно, что в статье в которой рассказывается “как выполнять вычисления...” вы увидите значительное количество кода Mathematica, но я начну с простых вступительных объяснений.

Предположим, что вы делаете линии рисунка карандашом на листке бумаги и допустим, что рисуете только линии; никакую штриховку и никакое заполнение не делаете. Тогда рисунок будет выполнен из ряда сегментов кривой. Математическое понятие, такое как ряды Фурье позволяет нам записывать конечную математическую формулу для каждого из этих линейных сегментов, которые будут описывать их как угодно точно.

В качестве простого примера рассмотрим ряд функций ,



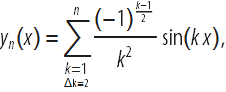
которые являются суммой синусоид различных частот и амплитуд. Вот первые несколько членов этой последовательности функций:







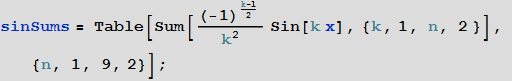
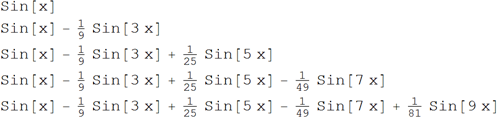
Графическое построение этой последовательности функций показывает, что с увеличением n функция стремится к треугольной функции.





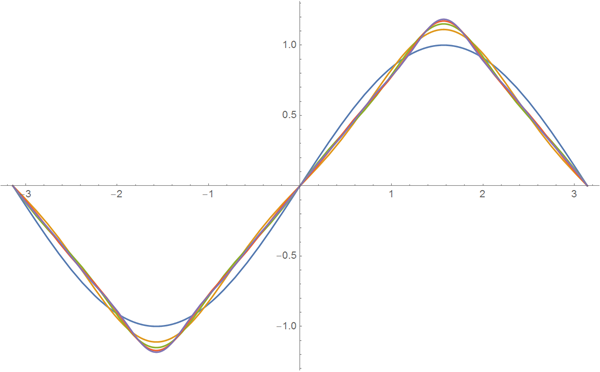
Функция синуса является нечётной функцией, и в результате любые суммы функций вида sin(kx) также являются нечётными функциями. Если мы используем функцию косинуса, то вместо этого получим чётные функции. Композиция из значений синусов и косинусов позволяет нам аппроксимировать более общие формы кривых.

Обобщая вышесказанное, заменим множить в рассматриваемом ряду на , а также зададим два ряда, от синусов и косинусов, соответственно:



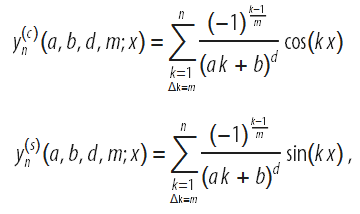
Данные функции позволяют аппроксимировать более широкий класс функций:





Можно показать, что любая гладкая кривая y(x) может быть сколь угодно хорошо аппроксимирована на любом интервале с помощью рядов Фурье. Причем для гладких кривых значения коэффициентов sin(k x) и cos(k x) стремятся к нулю при больших значениях k.

Теперь, рассматривая параметрическую кривую , мы можем использовать такого рода суперпозиции функций синусов и косинусов независимые для горизонтальной и вертикальной составляющих.

Использование суммы трёх синусов и трёх косинусов в каждой из компонент уже охватывает большое разнообразие форм, включая круги и эллипсы:



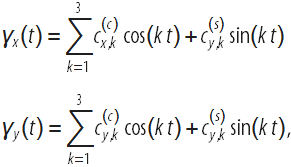
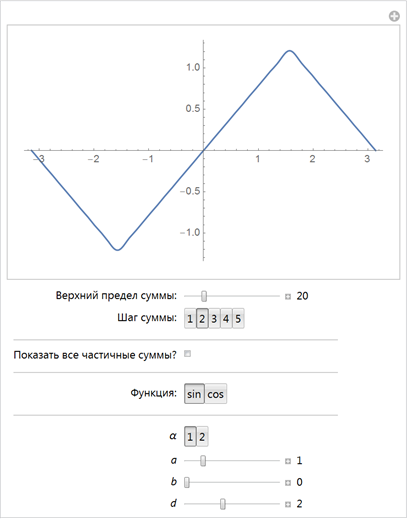
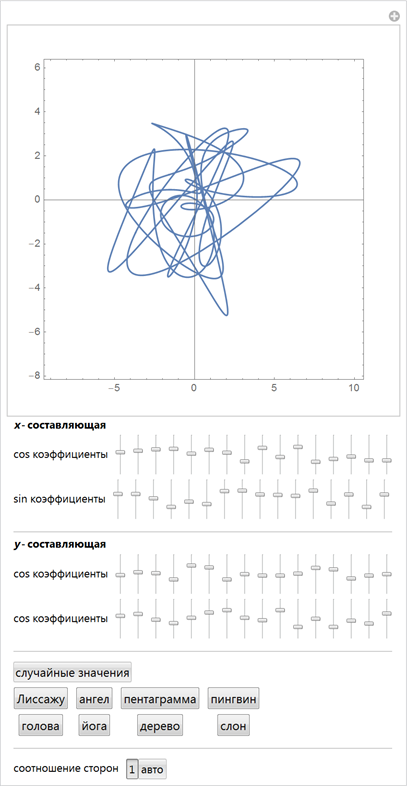
Следующая интерактивная демонстрация позволяет нам исследовать пространство возможных форм. 2D слайдеры изменяют соответствующие коэффициенты перед функциями косинуса и синуса:





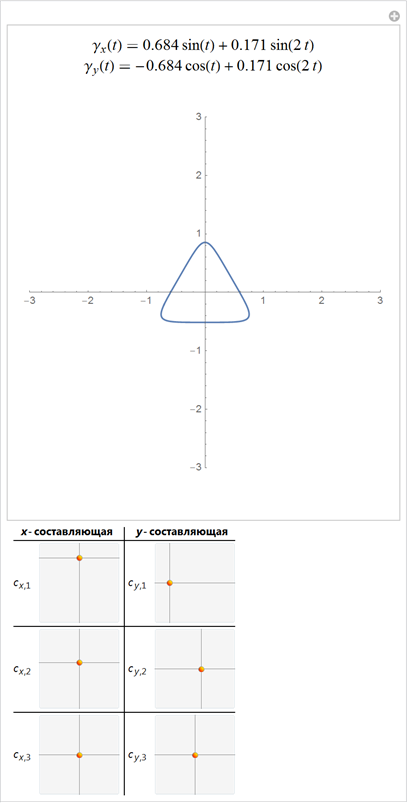
Если мы оборвём разложение в ряд Фурье кривой, скажем на первых n членах ряда, мы получим 4n свободных параметров. В пространстве всех возможных кривых, большинство кривых будут выглядеть неинтересно, но при некоторых значениях коэффициентов, разложения будут иметь вид фигур, в которых можно будет увидеть знакомые формы. Однако, даже небольшие изменения в коэффициентах разложения сильно меняют фигуру. Следующий интерактивный пример позволяет менять начальные 4?16=64 коэффициента ряда Фурье кривой. Используя особые наборы коэффициентов рядов Фурье, мы можем получить различные узнаваемые фигуры.





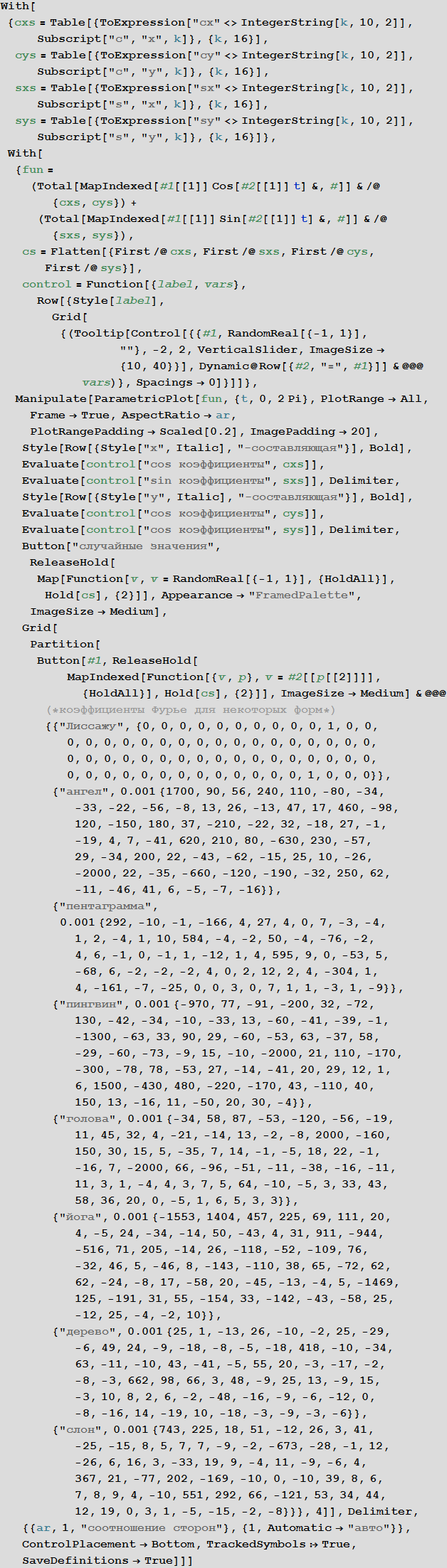
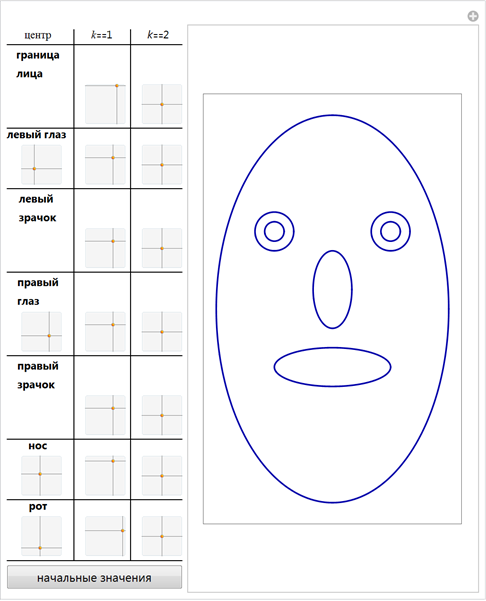
Если мы возьмём теперь более одной кривой, мы будем иметь все необходимые компоненты для построения похожего на лицо изображения. В следующей интерактивной демонстрации используется два глаза, два зрачка, нос и рот.





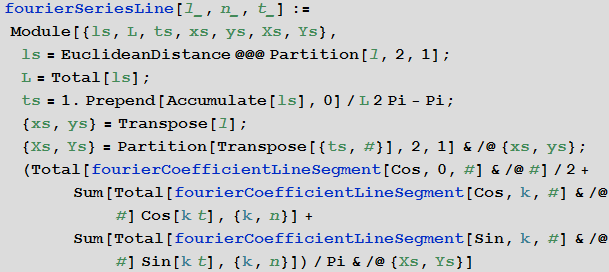
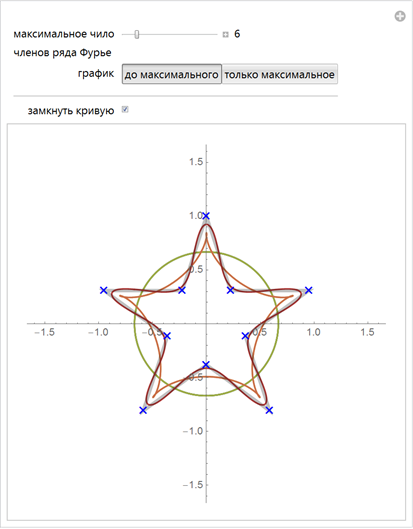
Теперь сделаем обратное: расположим ряд точек (синие крестики) так, чтобы образовалась линия, которую можно будет менять и построим кривую, которая будет приближать заданную кривую рядами Фурье:









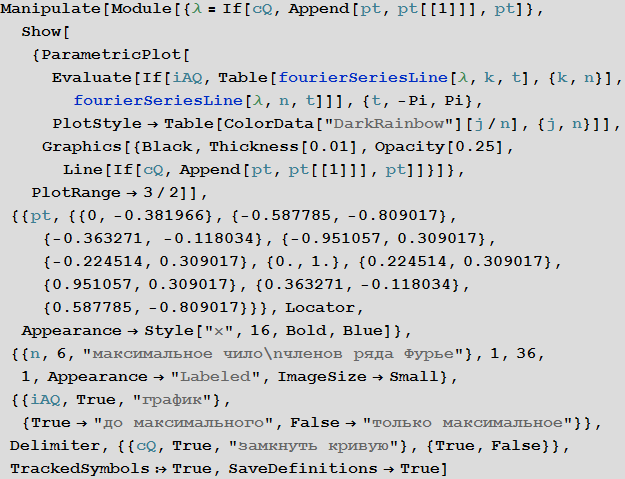
Примечание: ряды Фурье — это не единственный способ задания аппроксимирующих кривых. Мы могли бы использовать вейвлеты или сплайны, или кодировать кривые кусочно через круговые сегменты. Или при достаточном терпении, с помощью универсальности дзета-функции Римана, мы могли бы найти любую фигуру внутри критическую полосы. (Как ни удивительно, любое возможное (достаточно гладкое) изображение, такое как Иисус на тосте, существует при некоторых значениях дзета-функции Римана ?(s) в полосе 0?Re(s)?1, но у нас нет конструктивного способа, чтобы найти его.)

Чтобы продемонстрировать как найти простые, основанные на ряде Фурье формулы, которые приближают данные фигуры, мы начнём с примера: фигура с точными, чётко определёнными границами — короткая формула. Более конкретно, мы будем использовать известную формулу: теорему Пифагора.





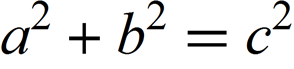
Растеризация уравнения даст исходное изображение, которое мы будем использовать:





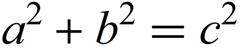
Легко можно получить набор всех точек, описывающих края символов, с помощью функции EdgeDetect.









Теперь, когда у нас есть точки, которые задают края, мы можем соединить их прямыми (или криволинейными) сегментами. Следующая ниже функция pointListToLines осуществляет эту операцию. Мы начинаем со случайно выбранной точки и найдем все ближайшие точки к ней (используя быструю функцию Nearest). Мы продолжим этот процесс до тех пор, пока не найдем точки все достаточно близкие точки. Также сделаем так, чтобы не было разворотов на 180 градусов. Чтобы наблюдать за тем, как формируются кривые, мы используем функцию Monitor.



Для изображения записи теоремы Пифагора мы получаем 11 конкретных кривых из граничных точек.





Соединив наборы точек и раскрасив полученные кривые, мы увидим вполне ожидаемый набор кривых: внешние границы букв, внутренние границы букв a и b, три квадрата, плюс и знак равенства.





Теперь для каждого сегмента кривой нам потребуется найти ряд Фурье (x и y компоненты), который аппроксимирует сегмент. Руководствуясь обычным определением ряда Фурье функции f(x), мы знаем, что коэффициенты ряда являются интегралами от функции f(x), умноженной на cos(k x) и sin(k x). Но пока мы имеем множество точек, а не функции. Чтобы преобразовать их в функции, которые мы сможем интегрировать, создадим B-сплайны кривой для каждого ее сегмента. Параметризованная переменная B-сплайна кривой будет переменной интегрирования. (Использование B-сплайнов вместо кусочно-линейной интерполяции между точками даст нам дополнительные преимущества при аппроксимации сильно ломаных кривых.)





Мы можем найти интегралы, необходимые для получения коэффициентов Фурье с помощью численного интегрирования, однако, более быстрый способ заключается в использовании быстрого преобразования Фурье (FFT) для получения коэффициентов Фурье.

Для получения более однородных кривых мы выполним ещё один шаг: повторно параметризуем интерполированную кривую сплайна, состоящую из набора сегментов кривой, с помощью нового параметра — длины дуги. Функция fourierComponents реализует создание B-сплайна кривой, повторную параметризацию длиной дуги и вычисляет FTT для получения коэффициентов Фурье. Мы также учитываем открыт ли сегмент кривой или закрыт, чтобы избежать явления Гиббса. (Приведенная выше демонстрация аппроксимации пентаграммы хорошо показывает явление Гиббса в случае, если флажок “замкнуть кривую” снят.)









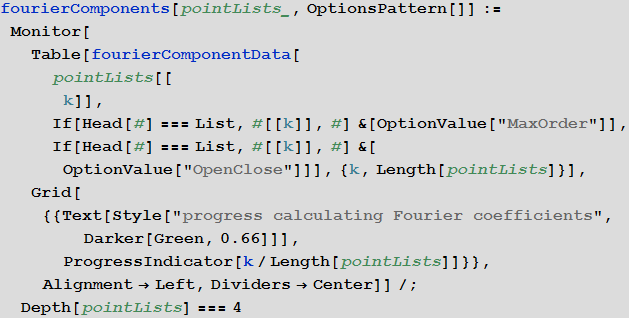
Для непрерывной функции мы ожидаем среднее значение скорости убывания для k-ого коэффициента ряда Фурье. Этот эффект должен сохраняться и для рассчитываемых нами коэффициентов ряда Фурье. Это означает, что в среднем на 10-й коэффициент Фурье приходится только 1% абсолютной величины по сравнению с первым. Это даёт возможность обрезать ряд Фурье на не очень высоких порядках, поскольку мы не хотим получать формулы, которые будут слишком большими. Выражение ниже вычисляет средний показатель степени скорости убывания Фурье-компонентов для вышеприведённой кривой . (Значение немного меньшее 2 объясняется дискретизацией точек в кривых B-сплайна.)





Ниже показан график в логарифмическом масштабе по обеим осям с абсолютными значениями коэффициентов ряда Фурье для первых трёх кривых. Вместе с тем общая тенденция относительно, скажем, квадратичного затухания для коэффициентов Фурье показывает, что величина соседних коэффициентов часто колеблется больше, чем среднее значение убыли коэффициентов в целом.





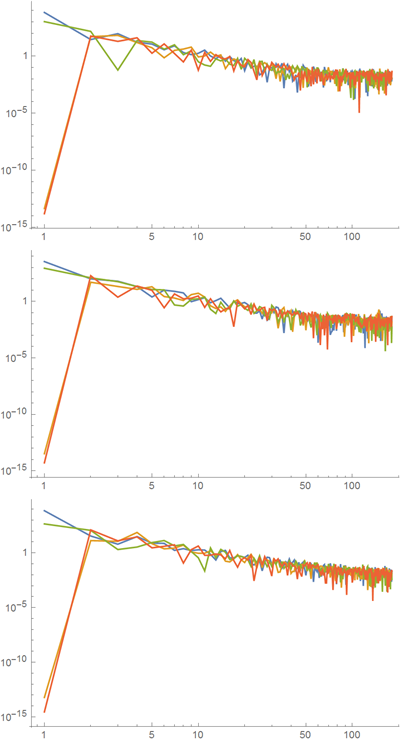
Умножение коэффициентов Фурье на cos(k t) и sin(k t) и суммирование этих выражений даёт нам желаемую параметризацию кривых.



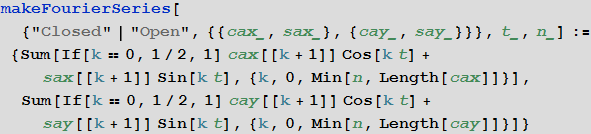
Функция makeFourierSeriesApproximationManipulate визуализирует приближения кривой в зависимости от того, сколько членов ряда берется.



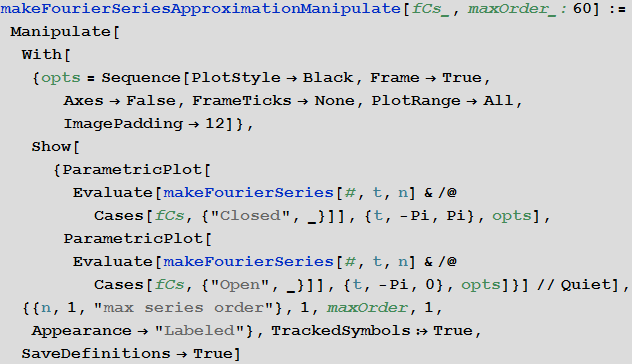
Для картинки, соответствующей теореме Пифагора, начиная с десятка эллипсов, мы быстро формируем исходное изображение, увеличивая количество членов ряда Фурье.





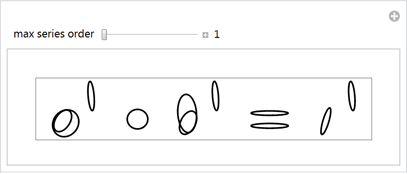
Мы хотим определить аналитическое выражение для всего уравнения, даже если это выражение будет состоять из не пересекающихся сегментов кривой. Для достижения этого, мы используем периодичность членов ряда Фурье, имеющих период 2?, для того, чтобы изобразить каждый из сегментов на соответствующем отрезке: [0,2?], [4 ?, 6 ?], [8 ?, 10 ?], …, а в интервалах (2?,4?), (6 ?, 8 ?), …, мы будем иметь чисто мнимые координаты кривой. На этих отрезках кривая не может быть изображена, а значит, мы получаем набор не пересекающихся сегментов кривой. Ниже эта конструкция показана для набора из двух окружностей:







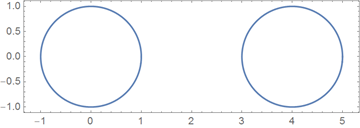
График ниже показывает отдельно действительные и мнимые части из комплексозначной параметризации, построенной выше. Красная линия показывает чисто мнимые значения параметра из интервала [2?,4?].





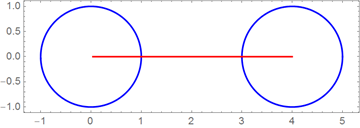
Так как мы хотим, чтобы заключительная формула для кривых выглядела настолько коротко и просто насколько это возможно, мы заменяем сумму в формуле a cos(k t) + b sin(k t) на A sin(k t+?) используя функцию sinAmplitudeForm, а также округляем приближенные коэффициенты ряда Фурье до ближайших рациональных чисел. Вместо Piecewise, мы используем функцию UnitStep в окончательной формуле, чтобы отделить друг от друга разные сегменты кривой. Вещественные сегменты мы перечисляем в явном виде, а все сегменты, которые не должны быть нарисованы задаются через выражение .







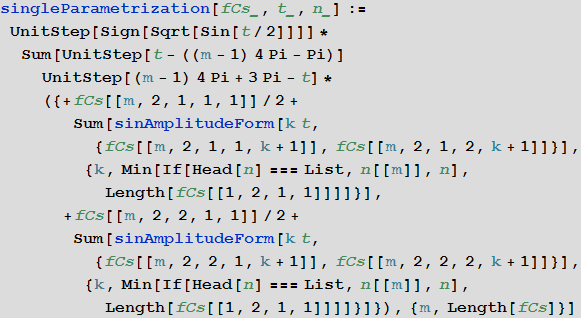
Теперь у нас есть всё, чтобы записать заключительную параметризацию {x(t),y(t)} картинки, на которой изображено равенство, задающее теорему Пифагора:











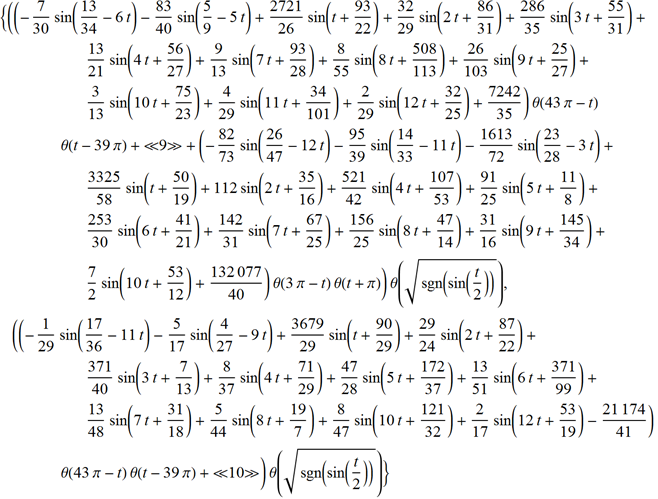
После того, как мы обсудили основные идеи составления параметризации, давайте рассмотрим более забавный пример, скажем Розовую пантеру. Просматривая результаты поиска изображения поисковой системой Bing, мы быстро находим изображение, которое подходит для параметризации в виде "замкнутой формы".

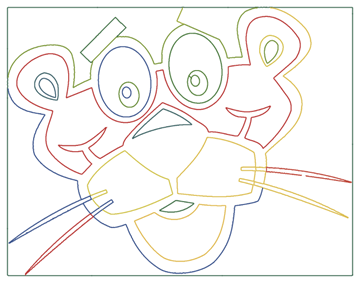
Давайте используем следующее изображение:





Применим функцию EdgeDetect для того, чтобы найти все границы лица пантеры.







Соединяя края кривой, получаем около 20 сегментов. (Изменив дополнительный второй и третий аргумент функции pointListToLines, мы получим меньшее или большее количество сегментов.)





Ниже каждый сегмент показан различным цветом. Мы видим, что некоторые замкнутые кривые являются результатом двух соединённых сегментов кривой; мы могли бы отделить их изменяя второй аргумент в функции pointListToLines. Но в нашей задаче это не особо важно.





Теперь делая все то, что было проделано ранее, несложно аппроксимировать сегменты кривой с помощью тригонометрических рядов.



Графическое изображение ряда показывает, что в случае, если берется 20 членов ряда на один сегмент, мы получим кривую, которая хорошо описывает о Розовую пантеру.











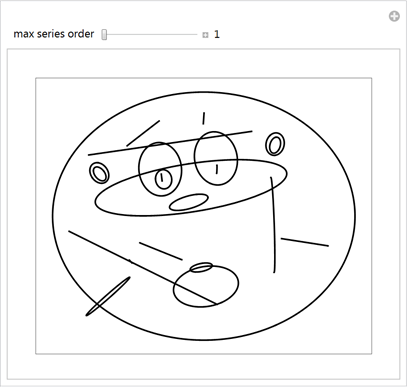
Ниже используются начальные значения количества членов ряда Фурье, используемых в каждом из сегментов, которые дают ясно распознаваемый рисунок Розовой пантеры.





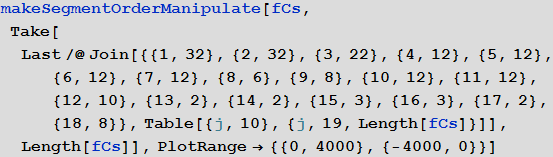
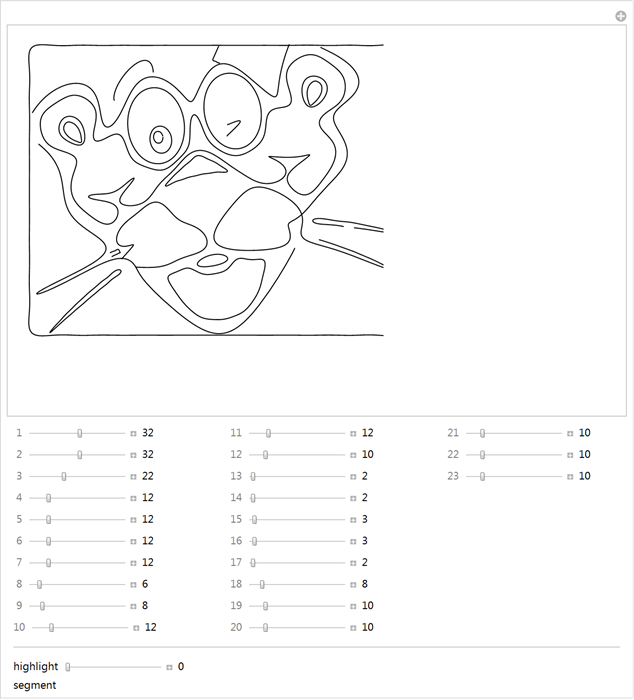
Для простых случаев мы можем теперь свернуть всю вышеупомянутую функцию в одну функцию. Заданная ниже функция makeSilhouetteFourierResult берет изображение в качестве своего аргумента. Данная функция в соответствии со следующей последовательностью действий: 1) вычисляет ряд Фурье; 2) возвращает в качестве результата участки ряда Фурье и интерактивную версию, которая позволяет нам изменить порядок ряда Фурье. Для простоты мы ограничиваем программу только для единственной кривой.



Вот четыре примера показывающие работу этой функции. Мы берем 4 изображения: паука; логотипа человека-паука; пары, танцующей танго и русалки.

























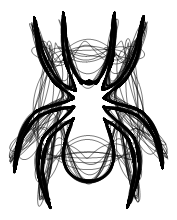
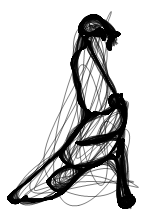
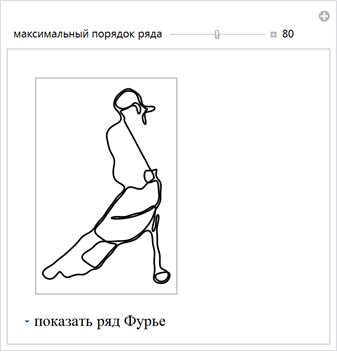
До сих пор начальные линейные сегменты были вычислены из изображений. Но мы также можем начать с нарисованных от руки кривых. Предположим, что мы хотим формулу для Исаака Ньютона. Так как я не силён в рисовании лиц, я немного смухлевал и использовал инструмент рисования кривых, чтобы нарисовать характерные линии лица и волос изображения сэра Исаака. (О алгоритмическом подходе к извлечению характерных линий лиц см. недавнюю статью Чжао и Чжу.) Вот изображение, которое мы будем использовать:





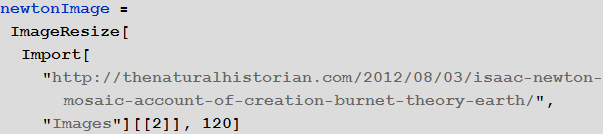
К счастью, небольшие случайные покачивания в нарисованной от руки кривой не будут иметь значения, так как они будут удалены, при опускании членов высших порядков в ряде Фурье.







Чтобы лучше увидеть нарисованные от руки кривые, мы отделяем изображение и линии.





На этот раз, у нас есть 16 сегментов. Мы создаём их ряд Фурье.



Ниже мы снова видим изображения, полученные с использованием различного количества членов ряда Фурье каждого из сегментов изображения:





Теперь используем различное количество членов ряда на разных сегментах. Для волос, мы используем довольно много членов ряда, а для глаз относительно мало. Это позволит гарантировать, что полученные уравнения лица не будут слишком большими.





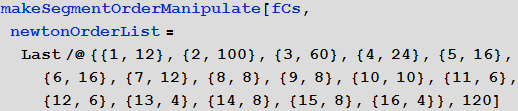
Ниже на одном графике показаны первые 50 приближений:





Итак, мы получили следующую формулу, описывающую образ сэра Исаака Ньютона:







А вот и график последнего параметрического представления:





На этом заканчивается сегодняшняя дискуссия о том, как построить кривые, которые напоминают лица людей, вымышленных персонажей, животных, или другие формы. В следующий раз мы будем обсуждать бесконечные графические возможности, которые возникают из приведенных формул и как вы можете использовать такого рода уравнения для самых разных изображений.