Перевод поста Джона Маклуна "Droste Effect with Mathematica". Код, приведенный в статье, можно скачать в конце поста.
Выражаю огромную благодарность Кириллу Гузенко за помощь в переводе.

---

Эффект Дросте (wiki) представляет собой рекурсивное включение изображением самого в себя. Название происходит от какао-порошка Droste, который в 1904 году продавался в упаковке, на которой была изображена медсестра, которая держала коробку, на которой была медсестра, ну и так далее. Самая простая реализация — отмасштабировать и трансформировать изображение, а затем поместить его на свою немодифицированную точную копию, затем начать процесс снова. Взгляните на демонстрацию, в которой используется оригинальные иллюстрации упаковки Droste. Однако значительно более интересных результатов можно достичь, если использовать теорию функций ко?мплексного переменного (ТФКП). Эшер М. К. был первым, кто популяризировал идею конформных отображений применительно к изображениям, однако с помощью компьютеров мы легко можем реализовать эту идею на фотографиях для получения чего-то подобного:



Да, идея не нова. Однако, когда я решил реализовать подобный эффект, те методы, что я находил в сети, казались мне неудовлетворительными. Одни предполагали много ручной работы типа «скопируй-вставь» над изображениями, в других были проблемы с несоответствием разрешений на стыках частей изображений. И, как обычно, я пришёл к тому, что тут надо использовать Mathematica, или в данном случае gridMathematica.

По сути идея проста. Мы создаем изображение, где пиксель в позиции {x,y} получаемого изображения получается из пикселя в позиции f[{x,y}] нашего исходного изображения. Магия заключается в выборе самой функции f. Но прежде чем мы добираемся до этого, нам нужно кое-что подготовить.

В настоящее время Mathematica не содержит операции по произвольной трансформации изображений, так что для начала я должен их реализовать (Пост написан Джоном в 7-й версии Wolfram Mathematica, в 8-й версии для этих целей появилась специальная функция ImageTransformation, которая заметно уменьшает объем кода в статье Джона — прим. ред.). Важный момент заключается в постоянном вычислении цвета между пикселями для предотвращения проблем соответствия разрешения и ненужной пикселизации в увеличенных областях изображения. Мой метод заключается в линейной интерполяции всех цветов пикселей в каждом канале RGB для изображения. Это наиболее вычислительно сложный подход, особенно с исходными изображениями в 10 мегапикселей, однако он дает необходимое мне качество.



Чтобы компенсировать подобный подход, я настроил всё для параллельных вычислений. Для начала, я использовал встроенные в Mathematica инструменты распараллеливания. Таким образом, вместо того, чтобы просто использовать Table для генерации сетки пикселей, я создал функцию, вызывающую Table для генерации слоя окончательного изображения, которая вызывается параллельно посредством ParallelTable для перераспределения работы между несколькими ядрами процессора. Так на 3-4 строчки больше, однако это лишь половина работы по распараллеливанию.





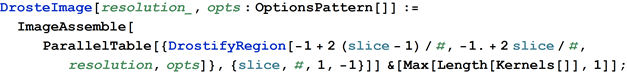
Затем, я передаю исходное изображение каждому процессору и задаю функцию интерполяции. Эта часть весьма требовательна к вычислениям, так что я хочу проделать это лишь раз и после этого иметь возможность делать любые виды изображений из исходного без проделывая повторно этой работы. Распараллеливание осуществляется здесь довольно просто: запускаются доступные ядра, осуществляется распределение определения программы на все ядра, а затем используется функция ParallelEvaluate для отправки изображения по ссылке с запросом на создание функции интерполяции.



Существует изящный приём в передаче изображения в виде строки с содержанием файла JPG вместо того, чтобы передавать реальные несжатые данные. Получается гораздо меньший объект, который, соответственно, быстрее передаётся.

При подобной настройке я легко могу привлекать дополнительные ядра компьютеров из своего офиса для ускорения вычислений посредством gridMathematica.

В код нужно ещё кое-что добавить. Так я избавляюсь от необходимости в том, чтобы исходное изображение было обрезано в правильном соотношении и с правильным центрированием.



Вот то, на что похоже мое исходное изображение после обрезки:



Что ж, всё скучное позади, теперь самое время поразвлечься.

Скручивание, которое я использую, основывается на специфических свойствах степенной функции Power на комплексной плоскости. Мы можем представить наши пары координат {x,y} как части комплексного числа p=x+Iy, использовать отображение f[p]:=p^c и вернуться обратно к декартовым координатам. Довольно трудно разобраться, каким брать значение c, особенно если использовать более общую модель a+(b+c p)^d, где {a,b,c,d} являются комплексными числами. Так что я решил обратиться к Wolfram Demonstrations Project, нашёл там демонстрацию с конформными отображениями и немного изменил код, чтобы получить интересующее меня отображение.

Поэкспериментировав, я выяснил влияния параметров, настроил калибровку, получил хорошие начальные значения и задал именованные опции в необходимых местах той самой магической формулы. В итоге, у меня получилось такая конструкция для скручивания.



Я обеспечиваю подобное самовоспроизведение перескакиванием внутрь при попытке получить доступ к пикселю за пределами изображения, а затем наружу во время получения доступа к пикселю внутри определённой области.

Из соображений эстетики я бы хотел закрыть соединения между изображениями для придания им большей естественности. В своём примере я использовал картинную рамку, однако я встречал примеры, где использовались дверные проёмы, окна, компьютерные мониторы и тому подобное.

Автоматизирование этого процесса позволяет избежать ручного копирования и последующей вставки, а также позволяет избежать проблем с несоответствием разрешений различных частей изображения.



Всё, вся трудоёмкая работа уже позади, теперь самое время побаловаться. Инициализируйте ядра с оригинальным изображением, задав координаты внутренней области (вы легко можете получить их, используя coordinate picker в палитре 2D Drawing):



Теперь сгенерируем изображение высотой в 400 пикселей в высоту:



Существует множество сочетаний параметров, например, как этот с двойной спиралью:



Одна спираль в противоположном направлении:



Без спиралей, одна лишь репликация:



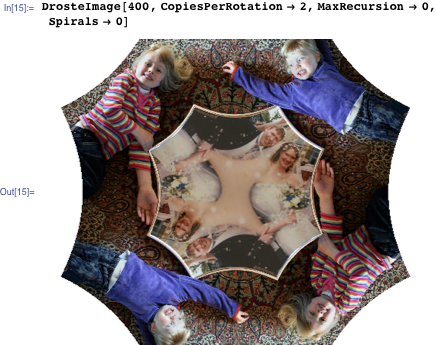
Этот код создаёт восьмиугольники путем создания двух копий на спираль:



А этот без рекурсии и спиралей — всего две копии, свёрнутые вместе:



И вот, кульминация — целый фильм в DVD качестве, показывающий эффект Дросте закручивания изображения в рекурсивную спираль.



Создание такого видео требует большого количества вычислений — вызов трёх интерполяционных функций для каждого из 10 млн. пикселей примерно по 400 тыс. раз для каждого из 60 кадров. Это тот момент, когда мои усилия по распараллеливанию действительно окупаются. Конечно, будучи в Wolfram Research, у меня есть под под рукой несколько лицензий gridMathematica, сообщающихся посредством Wolfram Lightweight Grid Manager (Начиная с 7-й версии Wolfram Mathematica, функционал по распараллеливанию включен в ядро Wolfram Language и не требует дополнительных программ при работе, он способен использовать все ядра, доступные на вашем компьютере. Однако, если есть необходимость подключиться к кластеру, для этого потребуется gridMathematica — прим. ред.). Я открываю Parallel Configuration preferences, и все они волшебным образом появляются. Несколько кликов, и вот у меня появляются ещё 16 ядер, вдобавок к двум на моём маленьком ноутбуке, и без каких бы то ни было изменений в коде фильм генерируется в 8 раз быстрее (и в 16 раз быстрее чем без распараллеливания). Я точно не знаю, где именно работает этот код, но так как программа и исходные изображения передаются автоматически, то мне это не особо и интересно. Можете посмотреть экранную демонстрацию того, как всё это настраивается.



Этот код можно по разному модифицировать; например, изменение ReplicateRegion позволит использовать непрямоугольные кадры, в виде кругов, например, или можно даже изменять цвета и прозрачность репликаций. Попробуйте самостоятельно поэкспериментировать и посмотреть, что может из этого получиться.