Вот полная реализация этого алгоритма:
float FastInvSqrt(float x) {
float xhalf = 0.5f * x;
int i = *(int*)&x; // представим биты float в виде целого числа
i = 0x5f3759df - (i >> 1); // какого черта здесь происходит ?
x = *(float*)&i;
x = x*(1.5f-(xhalf*x*x));
return x;
}Этот код вычисляет некоторое (достаточно неплохое) приближение для формулы
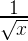
Сегодня данная реализация уже хорошо известна, и стала она такой после появления в коде игры Quake III Arena в 2005 году. Её создание когда-то приписывали Джону Кармаку, но выяснилось, что корни уходят намного дальше – к Ardent Computer, где в середине 80-ых её написал Грег Уолш. Конкретно та версия кода, которая показана выше (с забавными комментариями), действительно из кода Quake.
В этой статье мы попробуем разобраться с данным хаком, математически вывести эту самую константу и попробовать обобщить данный метод для вычисления произвольных степеней от -1 до 1.
Да, понадобится немного математики, но школьного курса будет более, чем достаточно.
Зачем?
Зачем вообще нам может понадобиться считать обратный квадратный корень, да ещё и пытаться делать это настолько быстро, что нужно реализовывать для этого специальные хаки? Потому, что это одна из основных операций в 3D программировании. При работе с 3D графикой используются нормали поверхностей. Это вектор (с тремя координатами) длиной в единицу, который нужен для описания освещения, отражения и т.д. Таких векторов нужно много. Нет, даже не просто много, а МНОГО. Как мы нормализуем (приводим длину к единице) вектор? Мы делим каждую координату на текущую длину вектора. Ну или, перефразируя, умножаем каждую координату вектора на величину:
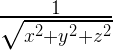
Расчёт
 относительно прост и работает быстро на всех типах процессоров. А вот расчёт квадратного корня и деление – дорогие операции. И вот поэтому – встречайте алгоритм быстрого извлечения обратного квадратного корня — FastInvSqrt.
относительно прост и работает быстро на всех типах процессоров. А вот расчёт квадратного корня и деление – дорогие операции. И вот поэтому – встречайте алгоритм быстрого извлечения обратного квадратного корня — FastInvSqrt.Что он делает?
Что же делает вышеуказанная функция для вычисления результата? Она состоит из четырёх основных шагов. Первым делом она берёт входное число (которое пришло нам в формате float) и интерпретирует его биты как значение новой переменной i типа integer (целое число).
int i = *(int*)&x; // представим биты float в виде целого числаДалее над полученным целым числом выполняется некоторая целочисленная арифметическая операция, которая работает достаточно быстро и даёт нам некоторую аппроксимацию требуемого результата
i = 0x5f3759df - (i >> 1); // какого черта здесь происходит ?То, что мы получили в результате данной операции, ещё не является, собственно, результатом. Это лишь целое число, биты которого представляют некоторое другое число с плавающей запятой, которое нам нужно. А значит, необходимо выполнить обратное преобразование int во float.
x = *(float*)&i;И, наконец, выполняется одна итерация метода Ньютона для улучшения аппроксимации.
x = x*(1.5f-(xhalf*x*x));И вот теперь у нас имеется отличная аппроксимация операции извлечения обратного квадратного корня. Последняя часть алгоритма (метод Ньютона) – достаточно тривиальная вещь, я не буду на этом останавливаться. Ключевой частью алгоритма является шаг №2: выполнение некоторой хитрой арифметической операции над целым числом, полученным от интерпретации битов числа с плавающей запятой в качестве содержимого типа int. На этом мы и сфокусируемся.
Какого черта здесь происходит?
Для понимания дальнейшего текста нам нужно вспомнить формат, в котором хранятся в памяти числа с плавающей запятой. Я опишу здесь только то, что важно здесь для нас (остальное всегда можно подсмотреть в Википедии). Число с плавающей запятой хранится как комбинация трёх составляющих: знака, экспоненты и мантиссы. Вот биты 32-битного числа с плавающей запятой:

Первым идёт бит знака, дальше 8 битов экспоненты и 23 бита мантиссы. Поскольку мы здесь имеем дело с вычислением квадратного корня, то я предположу, что мы будем иметь дело лишь с положительными числами (первый бит всегда будет 0).
Рассматривая число с плавающей запятой как просто набор битов, экспонента и мантисса могут восприниматься как просто два положительных целых числа. Давайте обозначим их, соответственно, Е и М (поскольку дальше мы будем часто на них ссылаться). С другой стороны, интерпретируя биты числа с плавающей запятой, мы будем рассматривать мантиссу как число между 0 и 1, т.е. все нули в мантиссе будут означать 0, а все единицы – некоторое число очень близкое (но всё же не равное) 1. Ну и вместо того, чтобы интерпретировать экспоненту как беззнаковое 8-битное целое число, давайте вычтем смещение (обозначим его как В), чтобы получить знаковое целое число в диапазоне от -127 до 128. Давайте обозначим float-интерпретацию этих значений как е и m. Чтобы не путаться, будем использовать прописные обозначения (Е, М) для обозначения целочисленных значений и строчные (е, m) – для обозначения чисел с плавающей запятой (float).
Преобразование из одного в другое тривиально:
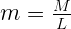
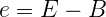
В этих формулах для 32-битных чисел L = 2^23, а В = 127. Имея некоторые значения e и m, можно получить само представляемое ими число:
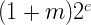
и значение соответствующей им целочисленной интерпретации числа:
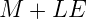
Теперь у нас есть почти все кусочки паззла, которые нужны для объяснения “хака” в коде выше. Итак, нам на вход приходит некоторое число х и требуется рассчитать его обратный квадратный корень:
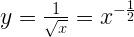
По некоторым причинам, которые вскоре станут понятны, я начну с того, что возьму логарифм по основанию 2 от обеих частей данного уравнения:
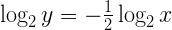
Поскольку числа, с которыми мы работаем, на самом деле являются числами с плавающей запятой, мы можем представить х и у согласно вышеуказанной формуле представления таких чисел:
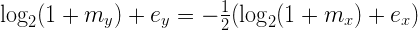
Ох уж эти логарифмы. Возможно, вы не пользовались ими со школьных времён и немного подзабыли. Не волнуйтесь, немного дальше мы избавимся от них, но пока что они нам ещё нужны, так что давайте посмотрим, как они здесь работают.
В обеих частях уравнения у нас находится выражение вида:
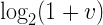
где v находится в диапазоне от 0 до 1. Можно заметить, что для v от 0 до 1 эта функция достаточно близка к прямой линии:
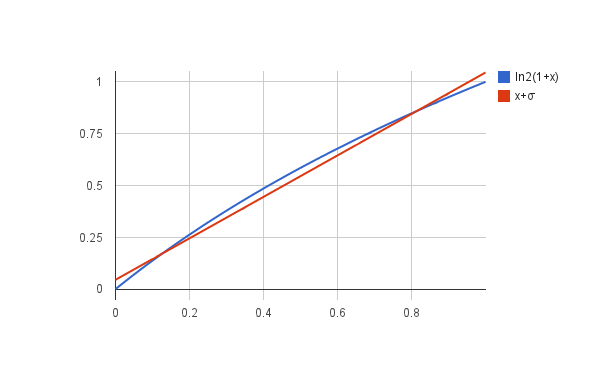
Ну или в виде выражения:

Где ? – некоторая константа. Это не идеальное приближение, но мы можем попытаться подобрать ? таким образом, чтобы оно было достаточно неплохим. Теперь, использовав его, мы можем преобразовать вышеуказанное равенство с логарифмами в другое, уже не строго равное, но достаточно близкое и, самое главное, СТРОГО ЛИНЕЙНОЕ выражение:

Это уже что-то! Теперь самое время прекратить работать с представлениями в виде чисел с плавающей запятой и перейти к целочисленному представлению мантиссы и экспоненты:

Выполнив ещё несколько тривиальных преобразований (можно пропустить детали), мы получим нечто, выглядящее уже довольно знакомо:

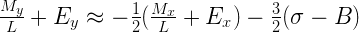

Посмотрите внимательно на левую и правую части последнего уравнения. Как мы видим, у нас получилось выражение целочисленной формы требуемого значения y, выраженное через линейного вида формулу, включающую целочисленное представление значения х:

Говоря простыми словами: “y (в целочисленной форме) – это некоторая константа минус половина от целочисленной формы х”. В виде кода это:
i = K - (i >> 1);Очень похоже на формулу в коде функции в начале статьи, правда?
Нам осталось найти константу K. Мы уже знаем значения B и L, но ещё не знаем чему равно ?.
Как вы помните, ? – это некоторое “поправочное значение”, которое мы ввели для улучшения аппроксимации функции логарифма к прямой линии на отрезке от 0 до 1. Т.е. мы можем подобрать это число сами. Я возьму число 0.0450465, как дающее неплохое приближение и использованное в оригинальной реализации. Используя его, мы получим:
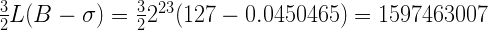
Угадаете, как число 1597463007 представляется в HEX? Ну, конечно, это 0x5f3759df. Ну, так и должно было получиться, поскольку я выбрал ? таким образом, чтобы получить именно это число.
Таким образом, данное число не является битовой маской (как думают некоторые люди просто потому, что оно записано в hex-форме), а результатом вычисления аппроксимации.
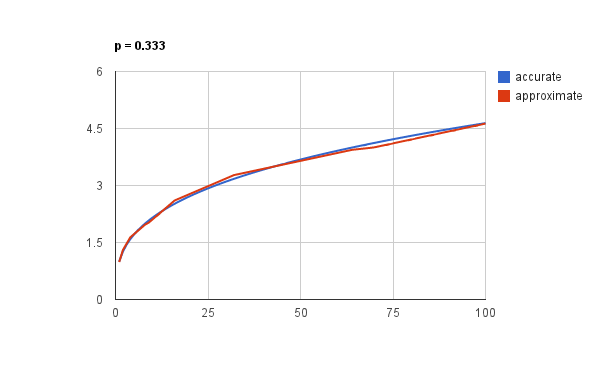
Но, как сказал бы Кнут: “Мы пока что лишь доказали, что это должно работать, но не проверили, что это действительно работает”. Чтобы оценить качество нашей формулы, давайте нарисуем графики вычисленного таким образом значения обратного квадратного корня и настоящей, точной его реализации:

График построен для чисел от 1 до 100. Неплохо, правда? И это никакая не магия, не фокус, а просто правильное использование несколько, возможно, экзотичного трюка с представлением чисел с плавающей запятой в виде целочисленных и наоборот.
Но и это ещё не всё!
Все вышеуказанные преобразования и выражения дали нам не только объяснение константы 0x5f3759df, но и ещё несколько ценных выводов.
Во-первых, поговорим о значениях чисел L и B. Они определяются не нашей задачей по извлечению обратного квадратного корня, а форматом хранения числа с плавающей запятой. Это означает, что тот же трюк может быть проделан и для 64-битных и для 128-битных чисел с плавающей запятой – нужно лишь повторить вычисления для рассчета других констант.
Во-вторых, нам не очень-то и важно выбранное значение ?. Оно может не давать (да и на самом деле – не даёт) лучшую аппроксимацию функции x + ? к логарифму. ? выбрано таким, поскольку оно даёт лучший результат совместно с последующим применением алгоритма Ньютона. Если бы мы его не применяли, то выбор ? являлся бы отдельной интересной задачей сам по себе, эта тема раскрыта в других публикациях.
Ну и в конце-концов, давайте посмотрим на коэффициент “-1/2” в финальной формуле. Он получился таким из-за сути того, что мы хотели вычислить (“обратного квадратного корня”). Но, в общем, степень здесь может быть любой от -1 до 1. Если мы обозначим степень как р и обобщим все те же самые преобразования, то вместо “-1/2” мы получим:
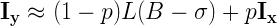
Давайте положим р=0.5 Это будет вычисление обычного (не обратного) квадратного корня числа:
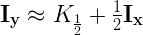
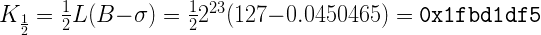
В виде кода это будет:
i = 0x1fbd1df5 + (i >> 1);И что, это работает? Конечно, работает:

Это, наверное, хорошо известный способ быстрой аппроксимации значения квадратного корня, но беглый гуглинг не дал мне его названия. Возможно, вы подскажете?
Данный способ будет работать и с более “странными” степенями, вроде кубического корня:


Что в коде будет выражено, как:
i = (int) (0x2a517d3c + (0.333f * i));К сожалению, из-за степени 1/3 мы не можем использовать битовые операции сдвига и вынуждены применить здесь умножение на 0.333f. Аппроксимация всё ещё достаточно хороша:
И даже более того!
К этому моменту вы уже могли заменить, что изменение степени вычисляемой функции достаточно тривиально меняет наши вычисления: мы просто рассчитываем новую константу. Это совершенно не затратная операция и мы вполне можем делать это даже на этапе выполнения кода, для разных требуемых степеней. Если мы перемножим две заранее известных константы:

То сможем вычислять требуемые значения на лету, для произвольной степени от -1 до 1:
i = (1 - p) * 0x3f7a3bea + (p * i);Чуть упростив выражение, мы даже можем сэкономить на одном умножении:
i = 0x3f7a3bea + p * (i - 0x3f7a3bea);Эта формула даёт нам “магическую” константу, с помощью которой можно рассчитывать на лету разные степени чисел (для степеней от -1 до 1). Для полного счастья нам не хватает лишь уверенности в том, что вычисленное таким образом приближенное значение может быть столь же эффективно улучшено алгоритмом Ньютона, как это происходило в оригинальной реализации для обратного квадратного корня. Я не изучал эту тему более глубоко и это, вероятно, будет темой отдельной публикации (наверное, не моей).
Выражение выше содержит новую “магическую константу” 0x3f7a3bea. В некотором смысле (из-за своей универсальности) она даже “более магическая”, чем константа в оригинальном коде. Давайте назовём её С и посмотрим на неё чуть внимательнее.
Давайте проверим работу нашей формулы для случая, когда p = 0. Как вы помните из курса математики, любое число в степени 0 равно единице. Что же будет с нашей формулой? Всё очень просто – умножение на 0 уничтожит второе слагаемое и у нас останется:
i = 0x3f7a3bea;Что, действительно является константой и, будучи переведённой во float-формат, даст нам 0.977477 – т.е. “почти 1”. Поскольку мы имеем дело с аппроксимациями – это неплохое приближение. Кроме того, это говорит нам кое-что ещё. Наша константа С имеет совершенно не случайное значение. Это единица в формате чисел с плавающей запятой (ну или “почти единица”)
Это интересно. Давайте взглянем поближе:
Целочисленное представление C это:

Это почти, но всё же не совсем, форма числа с плавающей запятой. Единственная проблема – мы вычитаем вторую часть выражения, а должны были бы её прибавлять. Но это можно исправить:
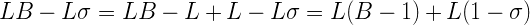
Вот теперь это выглядит в точности как целочисленное представление числа с плавающей запятой. Чтобы определить, какого именно числа, мы вычислим экспоненту и мантиссу, а потом уже и само число С. Вот экспонента:

А вот мантисса:
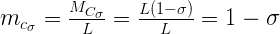
А, значит, значение самого числа будет равно:
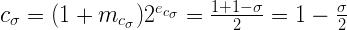
И правда, если поделить наше ? (а оно было равно 0.0450465) на 2 и отнять результат от единицы, то мы получим уже известное нам 0.97747675, то самое, которое “почти 1”. Это позволяет нам посмотреть на С с другой стороны и вычислять его на рантайме:
float sigma = 0.0450465;
float c_sigma = 1 - (0.5f * sigma);
int C_sigma = *(*int)&c_sigma;Учтите, что для фиксированного ? все эти числа будут константами и компилятор сможет рассчитать их на этапе компиляции. Результатом будет 0x3f7a3beb, что не совсем 0x3f7a3bea из расчетов выше, но отличается от него всего на 1 бит (наименее значимый). Получить из этого числа оригинальную константу из кода (и заголовка данной статьи) можно, умножив результат вычислений ещё на 1.5.
Со всеми этими выкладками мы приблизились к пониманию того, что в коде в начале статьи нет никакой “магии”, “фокусов”, “интуиции”, “подбора” и прочих грязных хаков, а есть лишь чистая математика, во всей своей первозданной красоте. Для меня главным выводом из этой истории стала новость о том, что преобразование float в int и наоборот путем переинтерпретации одного и того же набора бит – это не ошибка программиста и не “хак”, а вполне себе иногда разумная операция. Слегка, конечно, экзотическая, но зато очень быстрая и дающая практически полезные результаты. И, мне кажется, для этой операции могут быть найдены и другие применения – будем ждать.
Комментарии (109)

Halt
22.08.2017 13:50+18Со всеми этими выкладками мы приблизились к пониманию того, что в коде в начале статьи нет никакой “магии”, “фокусов”, “интуиции”, “подбора” и прочих грязных хаков, а есть лишь чистая математика, во всей своей первозданной красоте. Для меня главным выводом из этой истории стала новость о том, что преобразование float в int и наоборот путем переинтерпретации одного и того же набора бит – это не ошибка программиста и не “хак”, а вполне себе иногда разумная операция.
Ошибаетесь. В этом коде есть чудовищный и катастрофический хак, который просто обязательно надо было упомянуть. А именно, нарушение правила strict aliasing-а при разадресации указателя. Все беды в коде возникают оттого, что кто-то проникся «элегантным решением», не разобравшись во всех деталях, а потом начинает применять его к месту и не к месту.
Эту и другие темы я разбирал в своем докладе на конференции C++ Russia. Кому интересно, можете заглянуть.
Halt
22.08.2017 13:58+8Подробный разбор по strict aliasing-у можно найти в тексте другой моей статьи.

erlyvideo
23.08.2017 06:53а что поделать, тут пользуются аппаратным ускорением логарифмирования

Halt
23.08.2017 07:14+8Вопрос не в том, пользуются или не пользуются. Любое трюкачество должно быть уместно. А если его таки применяют, должен быть большой жирный комментарий, почему оно здесь и какие условия нужны для того чтобы все работало, включая фазы луны и прочее.
Код в статье будет работать, если компилятору передали ключ -fno-strict-aliasing, либо если эта опция умолчательная для компилятора.
Если через n лет проект начнут портировать на другую архитектуру (или переедут на другой компилятор) и забудут про этот маленький трюк, последствия могут оказаться самыми печальными.tangro Автор
23.08.2017 10:28Чтобы печальных последствий не было, достаточно 1-2 юнит-тестов. Если компилятор вдруг решит поменять размер int или стрюкачить с алиасингом — это произойдёт на этапе компиляции и легко отловится тестом.

Halt
23.08.2017 11:05+4К сожалению, этого не достаточно. Программа, содержащая неопределенное поведение — некорректна. Не существует никаких критериев, позволяющих доказать корректность программы, кроме формального анализа и ручного разбора ассемблера в данном конкретном случае. Даже компилятор сам не знает, есть ли там UB или нет.
Поменяв одно выражение в любой части кода вы можете повлиять на инлайнинг и как следствие на порядок выполнения проходов компилятора. Вам не доводилось видеть ситуацию, когда в программе выполняются обе ветви условия одновременно? Это один из возможных вариантов реакции компилятора на UB.
Выполняя оптимизации, компилятор исходит из предположения, что неопределенного поведения в программе нет. Соответственно абсолютно все действия, выполняемые компилятором, заботятся только об обеспечении наблюдаемого поведения. Код из статьи таковым не является.
Компилятор может изменять структуру программы так, чтобы сохранить наблюдаемое поведение и упростить себе жизнь. Под нож могут попадать выражения, условия, и даже целые функции. Представьте, что одним из таких условий был assert в вашем юнит тесте.
Резюмируя, юнит тест в таком случае даст не больше, чем комментарий «мамой клянусь, оно работает!». Даже хуже, проход тестов может вселить только ложную уверенность в том, что все хорошо.mayorovp
23.08.2017 11:36assert в тесте как раз защитить можно — надо только модуль с тестами компилировать без оптимизации, и линковать с остальной программой динамически (или статически, но в два этапа — второй этап линковки уже без оптимизации).
Хуже другое — UB может никак не проявляться в тестах, но проявиться уже в реальной программе. Вот тут и правда никак не закрыться.

Halt
23.08.2017 11:46+1Идя таким путем, вы вступаете на очень зыбкую почву. Неизвестно еще, что будет хуже.
Если возникает объективная потребность в небезопасных манипуляциях, их нужно изолировать, вплоть до ручного написания функции на ассемблере.
Другое дело, что вся эта машинерия может негативно сказаться на производительности и потерять в итоге смысл.
Современные компиляторы достаточно умные, чтобы использовать весь набор доступных инструкций, включая уже названную rsqrtps. Главное просто не мешать и не считать себя умнее компилятора.

apro
24.08.2017 08:14+1а что поделать, тут пользуются аппаратным ускорением логарифмирования
можно написать так:
float FastInvSqrt(float x) { float xhalf = 0.5f * x; int32_t i; memcpy(&i, &x, sizeof(i)); // представим биты float в виде целого числа i = 0x5f3759df - (i >> 1); // какого черта здесь происходит ? memcpy(&x, &i, sizeof(x)); x = x*(1.5f-(xhalf*x*x)); return x; }
современный компилятор заинлайнит memcpy с фиксированным размером,
и в результате будет тот же код, что и задумывался,
зато ни UB, ни прочих непрятных эффектов
F0iL
23.08.2017 12:18Материалы по ссылкам прочёл, и даже понимание пришло в целом, но не могу понять, что конкретно не так в коде функции в статье? Типы примитивные, массивов нет, компилятор поместит i и x в регистры или на стеке… и что не так? Ради интереса скомпилировал тест с -O3 и -O0 с включенным и выключенным алиасингом на g++ и clang++ (std=c++14) — результат выполнения одинаков. В чем должен быть подвох?

Halt
23.08.2017 12:33+2что конкретно не так в коде функции в статье?
Код в статье нарушает стандарт С++ и провоцирует UB. Дальше можно уже не разбираться, ибо на этом месте заканчиваются все гарантии.
Типы примитивные, массивов нет, компилятор поместит i и x в регистры или на стеке… и что не так?
Что именно компилятор будет делать со значениями зависит от сотни-другой параметров, включая оценку весов при инлайнинге и register pressure в данной точке. Сама попытка объяснить, что сделает компилятор из общих соображений и «здравого смысла» уже обречена на провал.
Ради интереса скомпилировал тест с -O3 и -O0 с включенным и выключенным алиасингом на g++ и clang++ (std=c++14) — результат выполнения одинаков.
То что он одинаков здесь и сейчас не значит, что он будет одинаков всегда. В этом и засада. Пример того, что может случиться, озвучивается в докладе в районе 28 и 29 слайдов.
К сожалению, самое страшное, что может сделать программист в непонятной ситуации, — «это проверить на практике и убедиться, что все хорошо».
F0iL
23.08.2017 13:13+1То что это нарушение стандарта и UB — это с самого начала было понятно, интересно было как раз увидеть реальный пример «что конкретно может пойти не так», для этого, собственно, и пробовал скомпилировать с разными ключами, чтобы получить разные результаты и пройтись потом по отладочному выводу.
mayorovp
23.08.2017 12:35+1Код основан на трюке с обращением к float через указатель на int:
int i = *(int*)&x;,x = *(float*)&i;. Вот это и есть "не так".
Подвох в том, что эта операция — по стандарту UB (нарушение strict aliasing rule). Некоторые компиляторы имеют ключи для отключения этого правила или вообще не учитывают его при оптимизациях, потому код и работает. Но такой код является непереносимым не только на другие платформы, но даже на новую версию компилятора.

lieff
23.08.2017 12:36+1Подвох в том, что по стандарту это UB. Несмотря на то что указатель скастили вот только что — на указателях этих есть пометка, что они гарантированно не пересекаются (когда они гарантированно пересекаются), нарушается правило strict aliasing стандарта. Кстати в статье не указан еще один метод: пометить указатели как могущие пересекаться __attribute__((__may_alias__)), но это уже расширение.

netch80
23.08.2017 15:50В ряде источников (например, тут) сказано, что обходить проблему strict aliasing можно надёжно через union?ы — правда, сказано это для C, а не C++. У Вас утверждается, что union только условно безопасен. Кому верить и отчего это зависит?

Halt
23.08.2017 17:01На том же Stackoverflow есть хороший вопрос после которого понятно, что ничего непонятно.
Очевидно, что верить нужно стандарту, вот только пользуемся мы продуктами интерпретации оного, так что правильного ответа я не знаю.
Но судя по изменениям, движемся мы в сторону разрешения type punning через union.
khim
24.08.2017 00:52+2Кому верить и отчего это зависит?
От компилятора. GCC разрешает подобные трюки, правда с оговорками, clang — нет.
Непонятно, впрочем, зачем всё это, если есть переносимая реализация:
Смотрите сами$ cat cast.cc #include <string.h> int float_to_int(float x) { int result; memcpy(&result, &x, sizeof(float)); return result; } khim@khim:~/work/android/android-standalone/prebuilts/clang/host/linux-x86/clang-4053586/bin$ ./clang++ -O3 -S cast.cc -o- | c++filt .text .file "cast.cc" .globl float_to_int(float) .p2align 4, 0x90 .type float_to_int(float),@function float_to_int(float): # @float_to_int(float) .cfi_startproc # BB#0: movd %xmm0, %eax retq .Lfunc_end0: .size float_to_int(float), .Lfunc_end0-float_to_int(float) .cfi_endproc .ident "Android clang version 5.0.300080 (based on LLVM 5.0.300080)" .section ".note.GNU-stack","",@progbits
Halt
24.08.2017 07:34+2А самое главное, любой читающий код поймет, что тут происходит, даже без пояснений. Главное не подпускать к коду тех, кто вопит про неэффективность и упущенную
прибыльвозможность оптимизации :)
Хотя, конечно, по-прежнему остается проблема разных размеров. Кэп подсказывает, что надо добавить ассерт, плюс использовать типы с фиксированным размером, вроде uint32_t.khim
24.08.2017 19:29Главное не подпускать к коду тех, кто вопит про неэффективность и упущенную прибыль возможность оптимизации :)
Нет никакой «упущенной прибыли». Даже самый последний MSVC научился сmemcpyработать несколько лет назад. Покажите им сгененированный ассеблерный код — и они умолкнут.
Кэп подсказывает, что надо добавить ассерт, плюс использовать типы с фиксированным размером, вроде uint32_t.
Не бывает флоатов фиксированного размера в стандарте, увы. А вотstatic_assert— это да.
Xandrmoro
22.08.2017 13:51+4> Со всеми этими выкладками мы приблизились к пониманию того, что в коде в начале статьи нет никакой “магии”
Скорее, наоборот, я ещё больше укрепился в том, что математика — это магия.windgrace
22.08.2017 17:20+10Третий закон Кларка, однако.
Any sufficiently advanced technology is indistinguishable from magic

Arastas
22.08.2017 13:52+2нам не хватает лишь уверенности в том, что вычисленное таким образом приближенное значение может быть столь же эффективно улучшено алгоритмом Ньютона
Я тут на прикинул на бумажке. Получается, что для возведения x в степень p, где p не ноль, шаг по Ньютону будет
 , где z это аргумент функции (который используется в оригинальном коде для вычисления xhalf). Похоже, что удобно будет только когда -1/p — положительное целое.
, где z это аргумент функции (который используется в оригинальном коде для вычисления xhalf). Похоже, что удобно будет только когда -1/p — положительное целое.
Browning
22.08.2017 14:27+18В блоке "интересные публикации" название статьи отображается переведённым в десятичную систему счисления. Exploitable?
michael_vostrikov
22.08.2017 17:12Возможно там при рендеринге есть что-то типа:
if (is_numeric($value)) echo (0 + $value);
Работает на PHP 5.6
tangro Автор
22.08.2017 18:13+4Администрация Хабра переименовала статью :)
Ну ок.
sebres
22.08.2017 19:18+3Интересно какие ксплойты повылазят, если опубликовать перевод к "0x5f3759df(appendix)"...
ReferenceError: appendix is not defined?
Ради какого-то там SEO портить авторскую задумку — несправедливо.
+1
Про заворотслепыхкишок у SEO-шников опосля второй статьи я помолчу лучше...

andy_p
22.08.2017 14:28+8Хорошо, что на данной платформе sizeof(int) == sizeof(float).

x893
22.08.2017 14:41+4Это надо в начале алгоритма поставить как assert, иначе долго будут искать причину гуру программирования когда неправильно считать будет.
khim
22.08.2017 19:55+2С современными компиляторами этот код вообще использовать нельзя, нарушения стандарта — они такие, да. Компилятор вполне может «соптимизировать» весь этот код в «return 0».

x893
22.08.2017 21:04Что то меня терзают сомнения на тему таких умных компиляторов. Может конечно алгоритмы которые в шахматы выигрывают и скомпилируют в return 0, но те что в шашки — точно так не смогут. Да и отладчик с #pragma останется всегда. На крайняк и на ассемблере можно наколбасить. На нём уж точно замучаются оптимизировать.

dkozh
22.08.2017 22:08+1
И хотя более новые версии GCC так (пока) не делают, такое поведение формально не противоречит стандарту, потому что в результате undefined behaviour может получиться все, что угодго (по факту оптимизатор решил, что
(unsigned short *)&aи&aне алиасятся, и решил переставить инструкции местами, потому что почему бы и нет).
symbix
23.08.2017 00:08-3Я ненастоящий сварщик, но — volatile проставить и все, не?
agmt
23.08.2017 11:37+2Не уверен, станет ли валиднее код, но медленнее — точно.

netch80
23.08.2017 15:44Доступ к памяти всё равно пройдёт через кэш, потеря будет в пару тактов на операции — это малосущественно.
А ещё — для реализации под конкретный процессор можно вставить операцию местного ассемблера, и volatile не потребуется :)

sebres
23.08.2017 16:25-2volatile нужен platform-agnostic, multi-threaded ONLY.
Грубо говоря не даст прочитать некоторому потоку (соптимизированное компилятором) промежуточное значение (явно не указанный программистомv1 = v2) или не даст вырезать (оптимизировать до 0 инструкций) неочевидную для компилятора установку такой переменной.
Грубо говоря, он думает что переменная тут (или ниже) не используется (этим потоком), зато может вполне себе — другим.
Т.е. конкретно тут — ни о чем...
khim
С современными компиляторами этот код вообще использовать нельзя
Компилятор вполне может «соптимизировать» весь этот код в «return 0».С первым высказыванием согласиться могу, условно. Только не "нельзя" а не комильфо… И assert-ами обвязать желательно…
Со вторым не согласен в корне — с какого это перепуга он его вырежет?
В худшем случае UB (да и UB на касте int/float мне очень сомнительно)...
netch80
23.08.2017 16:39> Т.е. конкретно тут — ни о чем…
Конкретно тут — о том, что компилятор обязан записать в память то, что пишут по указателю volatile, сразу, не задерживаясь; и прочитать по другому volatile указателю, не делая никаких предположений, что по этому указателю и почему.
Этого достаточно, чтобы убрать проблему strict aliasing в компиляторе.
> volatile нужен platform-agnostic, multi-threaded ONLY.
К тредовости оно вообще-то отношения в C/C++ не имеет от слова «никак», пока пользуетесь стандартными механизмами вроде mutex lock/unlock.
(Это отличается, кстати, от Java — где на volatile нагрузили синхронизацию доступа между тредами.)
Компилятор не имеет права кэшировать чтение или запись переменной даже без volatile через вызов любой неизвестной компилятору функции с побочным эффектом изменения чего-то в памяти. Операции с мьютексами декларируются со свойством такого изменения, даже если они инлайнятся.
> В худшем случае UB (да и UB на касте int/float мне очень сомнительно)…
Таки может :(
sebres
23.08.2017 17:02-1К тредовости оно вообще-то отношения в C/C++ не имеет от слова «никак»
Да ну? А вы про атомарные операции (конструкты, инструкции) что-нибудь слышали?
Т.е. простейшие вещи (ака одна переменная типа int) вы правда мютексами защищаете?
Мютекс кстати тут вообще никаким местом и именно что "от слова никак", ибо если явно не указан volatile, то мютекс вокруг вам в случае не очевидной (нежелательной) оптимизации не поможет "от слова ничем"…
Например если компилятор выпилит установку переменной, как неиспользуемой далее.
Про остальное же я промолчу, да…
Например:
Компилятор не имеет права кэшировать чтение или запись переменной даже без volatile через вызов любой неизвестной компилятору функции
А то что эту функцию (неявно для компилятора) исполняет прямо сейчас другой поток, это куда?
Я вам еще раз повторю volatile однопоточно не интересен (ну если не нативно какой либо контроллер с мапой переменная<->чего-нибудь железное, что сравнимо с многопоточностью, ибо есть еще один актер)...
И да здесь не про Java...

netch80
23.08.2017 17:08> Да ну? А вы про атомарные операции (конструкты, инструкции) что-нибудь слышали?
«Мы» слышали. В том числе то, что атомарные переменные вообще-то не объявляют volatile, у них подобная функциональность заложена в штатные средства доступа.
> Т.е. простейшие вещи (ака одна переменная типа int) вы правда мютексами защищаете?
Давайте Вы внимательно прочтёте, на что отвечаете. А то такие Ваши домыслы, мягко говоря, удивляют.
> Например если компилятор выпилит установку переменной, как неиспользуемой далее.
Он не выпилит установку переменной, которая не локальная, потому что не следит за тем, кто её дальше будет использовать. Локальные для функции — они в таком обычно всё равно не участвуют (а если участвуют, это вообще-то не лучший стиль).
> А то что эту функцию (неявно для компилятора) исполняет прямо сейчас другой поток, это куда?
Какое отношение вообще имеет _исполнение_ функции в другом потоке? Или в Вашей обстановке у них при этом общие локальные данные?
> Я вам еще раз повторю volatile однопоточно не интересен
И я повторю, что он решает проблему со strict aliasing.
> Про остальное же я промолчу, да…
Настоятельно прошу вместо подобных «многозначительных» «умолчаний» вести обсуждение по сути.
sebres
23.08.2017 18:01В том числе то, что атомарные переменные вообще-то не объявляют volatile
Давайте Вы внимательно прочтёте, на что отвечаете.Вы про что вообще? Здесь вообще-то речь про
int i(который атомарный) и про функциюFastInvSqrt(в которой ни в каком её месте не нужен volatile от того самого слова).
Настоятельно прошу… вести обсуждение по сути.
По сути: расскажите где в этом куске из трех строчек нужен volatile и почему и где "компилятор обязан записать в память сразу"...
float FastInvSqrt(float x) { ... int i = *(int*)&x; i = 0x5f3759df - (i >> 1); x = *(float*)&i; ... }
Даже если компилятор соптимизирует это совсем без использования памяти (т.е. будет использовать например регистр EAX для преобразования — он обязан следовать логике преобразования для каста как написано (а не как вы думаете).
Т.е. для того-же x86:
; int i = *(int*)&x; mov eax,dword ptr [x] ; i = 0x5f3759df - (i >> 1); sar eax,1 mov ecx,5F3759DFh sub ecx,eax ; x = *(float*)&i; mov dword ptr [x],ecx
ВСЕ!
Причем здесь вообще "strict aliasing"? Тип int (как и float) не являются структурами...
Если вы про это, почему
mov dword ptr [x],ecxвместо например:
; x = *(float*)&i; mov dword ptr [i],ecx fld dword ptr [i] fstp dword ptr [x]
То и это совсем из другой оперы и не имеет ни к volatile ни к "strict aliasing", ни даже к выравниванию никакого отношения.
Под UB же я имел ввиду как раз например если типы для платформы есть не равной длинны, и/или для этой платформы биты перевернуты LSB/MSB или little-endian vs. big-endian или подобное (однако и тут при желании оно лечится двумя строчками обернутыми в #if… #endif).

netch80
23.08.2017 19:00> По сути: расскажите где в этом куске из трех строчек нужен volatile
Вы сузили контекст до конкретного куска кода. Этого не было в предыдущем обсуждении.
Если говорить об этом коде, то именно за счёт того, что x безусловно перетирается, проблемы нет.
Если же он был бы написан чуть-чуть иначе — например, было бы так
int i = *(int*)&x; i = 0x5f3759df - (i >> 1); *(int*)&x = i;
(одна только последняя строчка поменялась)
то проблема уже, очень вероятно, вылезла бы в полный рост, — компилятор мог бы просто не заметить, что x изменено. (Мало ли кто пишет чего по постороннему адресу...)
И GCC начинает об этом предупреждать — мне он на неё дословно сказал
fsq3.cc:3:19: warning: dereferencing type-punned pointer will break strict-aliasing rules [-Wstrict-aliasing] int i = *(int*)&x; // представим биты float в виде цел ^ fsq3.cc:5:11: warning: dereferencing type-punned pointer will break strict-aliasing rules [-Wstrict-aliasing] *(int*)&x = i; ^
К вопросу о том, структуры это или нет, это не имеет ни малейшего отношения. Коллега Halt в соседних комментариях приводил пример (в видео), как это реально влияло на каком-то компиляторе — аналогом для данной функции было бы, что код свернулся до { return x; }
К этому, все Ваши реплики как
> он обязан следовать логике преобразования для каста как написано (а не как вы думаете).
> Тип int (как и float) не являются структурами…
относятся к совсем другим аспектам, но не к этому.
А вот volatile помогло бы именно за счёт того, что запись в *(int*)&x переписало бы независимо от того, что компилятор думает о том, как относятся x и i друг к другу — он бы просто обязан был держать обоих в памяти и не делать никаких предположений о том, что x не изменилось, раз он не видит данного изменения. И это даже для локальных переменных. В выходном коде видно, что они явно пишут в память (в стек) и тут же из неё читают. Именно об этом я говорил как о «паре лишних тактов».
К счастью, пока что (?) встреченные Clang и GCC во всех тестах сумели как-то опознать, что это одна и та же сущность в памяти. Но гарантировать это я бы не пытался.
Если хотите возражать — прошу это делать со ссылками на стандарты (на публичные final drafts, если иного источника нет). Любая отсылка вида «у меня всё работает» тут, увы, совершенно непригодна.
sebres
23.08.2017 19:42+1Вы сузили контекст до конкретного куска кода. Этого не было в предыдущем обсуждении.
Чего это? Велось обсуждение конкретного куска кода из статьи — ничего я не "сужал"!
Мы что обсуждаем-то и где?
Во вторых там выше черным по белому стоит "конкретно тут — ни о чем…".
Вы же влезли в эту ветку с доказательствами "О чем, еще как о чем!" А потом выясняется, что для какого-то отстраненного теоретического случая (который здесь ни к месту и ни про то вовсе).
К этому, все Ваши реплики как относятся к совсем другим аспектам, но не к этому.
(Подавившись) вы очень нахальны, молодой человек...
*(int*)&x = i;
то проблема уже, очень вероятно, вылезла бы в полный рост, — компилятор мог бы просто не заметить, что x изменено.Да ну? А ничего что в данном случае его должно интересовать что
i(а неx) изменено, и "не заметить" этого компилятор ну никак не сможет (сдается мне сударь, вы не совсем понимаете о чем здесь пишете)…
Действительно есть такие компиляторы, которые при использования подобного "тухлого" каста (ударение на подобного) имеют UB (который описан у них в доку и как минимум выкинет warning при агрессивной оптимизации), но...
Но во вторых и у ув. мистера Уолша и у мистера Кармака хватило ума не использовать такой "гнилой" каст, и они таки написали
x = *(float*)&i;вместо вот этого вот*(int*)&x = i;.
Если хотите возражать — прошу это делать со ссылками на стандарты.
Я вам вовсе ничего не собираюсь не доказывать не возражать...
Для начала, что бы не быть голословным быть может вы мне приведете пример ("стандарт, публичные final drafts") где описан такой UB и на каком основании компилятор не заметит изменения "x" после даже такого "гнилого" каста и использует старое (не измененное) значение.
*(int*)&x = i; x = x*(1.5f-(xhalf*x*x));khim
24.08.2017 05:25+1Для начала, что бы не быть голословным быть может вы мне приведете пример («стандарт, публичные final drafts») где описан такой UB и на каком основании компилятор не заметит изменения «x» после даже такого «гнилого» каста и использует старое (не измененное) значение.
Да пожалуйста:
C99 – 6.5 Expressions
An object shall have its stored value accessed only by an lvalue expression that has one of the following types:
- a type compatible with the effective type of the object,
- a qualified version of a type compatible with the effective type of the object,
- a type that is the signed or unsigned type corresponding to the effective type of the object,
- a a type that is the signed or unsigned type corresponding to a qualified version of the effective type of the object,
- an aggregate or union type that includes one of the aforementioned types among its members (including, recursively, a member of a subaggregate or contained union), or
- a character type.
И сноска: The intent of this list is to specify those circumstances in which an object may or may not be aliased.
То есть стандарт явно разрешает считать что значениеxи значение*(int*)&xникак, совсем никак не связаны между собой. Равно как и значенияiи*(int*)&i. Тем самым вторая строка в этом примере — не зависит от первой и от параметров функции. А четвёртая строка — не зависит от третьей. То есть пару из второй и третьей строки можно вынести куда угодно. C учётом того, что значениеi, вычисленное в строке 4 ни на что не влияет вообще — можно эту пару строк и удалить…

sebres
23.08.2017 20:33Да кстати о птичках...
GCC… warning: dereferencing type-punned pointer will break strict-aliasing rules [-Wstrict-aliasing]
$ cd /tmp/ $ echo '#include <stdio.h> float FastInvSqrt(float x) { float xhalf = 0.5f * x; int i = *(int*)&x; i = 0x5f3759df - (i >> 1); x = *(float*)&i; x = x*(1.5f-(xhalf*x*x)); return x; } int main() { printf("fastinvsqrt of 9.0: %10.5f\n", FastInvSqrt(9.0)); return 0; } ' > test.c $ gcc -Wstrict-aliasing test.c -o test $ # и даже совсем усе-усе: $ gcc -Wall -Wextra test.c -o test $ ./test fastinvsqrt of 9.0: 0.33295
Чисто для самообразования… На которой версии gcc (и/или платформе) вы видите такое?
А то я перепробовал от 3.4 до 6.2 (linux, win, и от отчаянья даже mac и solaris), нигде не увидел...
sebres
23.08.2017 20:39Сорри за спам, забылось
-O2(вот блин что autoconf с людьми делает)…
Т.е. воспроизводится везде, начиная с 3.4…
Еще раз звиняюсь...
Scf
23.08.2017 20:43+1g++ -Wall -Wextra -O2 test.c -o test test.c: In function ‘float FastInvSqrt(float)’: test.c:5:19: warning: dereferencing type-punned pointer will break strict-aliasing rules [-Wstrict-aliasing] int i = *(int*)&x; ^ test.c:7:17: warning: dereferencing type-punned pointer will break strict-aliasing rules [-Wstrict-aliasing] x = *(float*)&i;
Правда, скомпилировать код так, чтобы он сломался, я не смог.
gcc (Ubuntu 5.4.0-6ubuntu1~16.04.4) 5.4.0 20160609
sebres
23.08.2017 21:52+1Покреативив вокруг да около, сделал чуть более "покладистый" вариант, вдруг кому буде нужно:
Example$ echo ' #include <stdio.h> #include <assert.h> #if defined(static_assert) || (__STDC_VERSION__ >= 201100L) static_assert(sizeof(int) == sizeof(float), "Cannot cast types of different sizes (int/float)"); #else #warning Unknown sizes of int/float to the compile time: assumed are equal (4/4). #endif float FastInvSqrt(float x) { char *buf = (char *)&x; float xhalf = 0.5f * x; int i = *(int*)buf; i = 0x5f3759df - (i >> 1); buf = (char *)&i; x = *(float*)buf; x = x*(1.5f-(xhalf*x*x)); return x; } int main() { printf("fastinvsqrt of 9.0: %10.5f\n", FastInvSqrt(9.0)); return 0; } ' > test.c; gcc -Ofast -Wall -Wextra test.c -o test; ./test
khim
24.08.2017 05:15Причем здесь вообще «strict aliasing»? Тип int (как и float) не являются структурами...
А какая разница? Strict aliasing гласит, что записать по адресу "(int*)&x" никак не может повлять на значение x!
он обязан следовать логике преобразования для каста как написано (а не как вы думаете).
С кастом — всё хорошо. С обращением в память — плохо.
В следующей программе:
Компилятор имеет право считать, что запись через "*p" и чтение через "*q" (и наоборот) никак друг с другом не связаны. То же самое — в исходной программе. В строке x = *(float*)&i; x получает некоторое значение — но, с точки зрения компилятора, точно не имеющее никакого отношения к тому, что находится вfloat x; float *q=&x int *p=(int*)&x; ...i. Стало быть манипуляции сi— можно перенести ниже. А поскольку строкаint i = *(int*)&x;инициализируетiкаким-то значением, не имеющим отношения к тому, что находится вi— то это значение тоже можно вынести «вниз». А другая фаза того же компилятора может заметить, после всего этого, что мы пишем вxзначение, которое ещё ничем не инициализировано вообще — ну так чего бы туда 0 не записать?
khim
24.08.2017 05:02+2Со вторым не согласен в корне — с какого это перепуга он его вырежет?
С целью оптимизации кода. Код, который нифига не делает — точно короче того, который что-то делает.
В худшем случае UB (да и UB на касте int/float мне очень сомнительно)...
Тут не каст int/float. Тут Type punning. В результате компилятор может, ну, например, переставить работу с целыми числами до работы с плавучкой или после.
То есть будет что-то подобное:
А после можно и «заметить» что мы обращаемся к неинициализированной переменной. Ну и раз мы всё равно можем вернуть что угодно — вернуть 0.float FastInvSqrt(float x) { int i; float xhalf = 0.5f * x; x = *(float*)&i; x = x*(1.5f-(xhalf*x*x)); i = *(int*)&x; // представим биты float в виде целого числа i = 0x5f3759df - (i >> 1); // какого черта здесь происходит ? return x; }
Iqorek
22.08.2017 17:22+4Есть какие то замеры производительности по сравнению с традиционным способом? С 2005 года и уж с тем более с 80х прошло много лет, может быть сегодня овчинка уже не стоит выделки?
tangro Автор
22.08.2017 18:13+1Что-то с 2005 года поменялось в теории сложности или архитектуре процессоров, что операции корня и деления стали работать быстрее суммирования и умножения? Вряд ли.
khim
22.08.2017 20:01+13Что-то с 2005 года поменялось в теории сложности или архитектуре процессоров
Таки даtangro Автор
22.08.2017 23:20Вот это да. И всё же вопрос был о сравнении с «традиционными способами», а вшитая в проц аппроксимация — это не оно.

netch80
23.08.2017 16:18Мнэээ…
1. Таки нет, чисто формально, ибо RSQRTPS — команда SSE1, а это 1999, а не 2005 :)
2. Вопрос был про «корня и деления» против «суммирования и умножения». Эти фокусы позволяют, например, ускорять деление через обратный корень, но с потерей точности — вот Intel про это пишет в 248966:
> In microarchitectures that provide DIVPS/SQRTPS with high latency and low throughput, it is possible to speed up single-precision divide and square root calculations using the (V)RSQRTPS and (V)RCPPS instructions. For example, with 128-bit RCPPS/RSQRTPS at 5-cycle latency and 1-cycle throughput or with 256-bit implementation of these instructions at 7-cycle latency and 2-cycle throughput, a single Newton-Raphson iteration or Taylor approximation can achieve almost the same precision as the (V)DIVPS and (V)SQRTPS instructions.
но всё равно это сильно дороже умножения…
В этом плане лучше поставить на оптимизацию Goldschmidt method — AMD клянётся, что получает на делении до 16 циклов на single, 20 на double, 24 на extended — это заведомо быстрее типичного SRT. И наверняка там ещё можно что-то выжать. (А для квадратного корня ещё быстрее получается.)
Обратная сторона — всё в плавучке — прибавлять 10 тактов на конверсию в обе стороны для целых это уже сравнимо с интеловским SRT…khim
24.08.2017 05:351. Таки нет, чисто формально, ибо RSQRTPS — команда SSE1, а это 1999, а не 2005 :)
AMD K6-III выпускались точно до 2000го года, а компьютеры, я думаю, продавались и позже.
но всё равно это сильно дороже умножения…
Не сильно. На каком-нибудь K7 RSQRTPS вообще быстрее умножения. Можете в таблички посмотреть.
На современных процессорах на оптимизацию подобных инструкций «забили», потому что кто же считает подобные вещи на CPU? Для этого GPU есть…
netch80
25.08.2017 09:25> На каком-нибудь K7 RSQRTPS вообще быстрее умножения.
Смешно — но показывает странное направление работы AMD.
> На современных процессорах на оптимизацию подобных инструкций «забили», потому что кто же считает подобные вещи на CPU? Для этого GPU есть…
Ну, похоже, не совсем. Например, после Nehalem повырезали много идиотизмов работы с денормализованными (там, где наследие K-C-S тратило тысячи тактов). Как минимум в SSE оба вендора не игнорируют плавучку. Но это происходит медленнее, чем хотелось бы…
ProLimit
22.08.2017 23:00Есть же еще математические сопроцессоры (FPU). Например, в STM32 вычисление квадратного корня занимает 14 тактов, что не так много. Деление — еще 14. Так что если нужен обратный квадратный корень — лучше взять этот алгоритм, если прямой — лучше вычислить на FPU.
Scf
22.08.2017 20:06+6Шикарно!
Поделюсь трюком, который я вычитал в исходниках Elite для zx spectrum: быстрое умножение двух однобайтных чисел.
ab = (a^2 + b^2 - (a-b)^2)/2
Эта формула элементарно выводится из школьного разложения квадрата разности. Т.е. можно быстро и точно умножать однобайтные числа, используя таблицу квадратов (512 байт)khim
22.08.2017 20:31+8Это было реально круто на процессорах Z80 или 6502, на которых отсутствовала операция умножения. Современные же процессоры перемножают числа за 2-3 такта, так что необходимость в подобных трюках, в общем и целом, отпала…
mayorovp
23.08.2017 08:36+1Современные процессоры реализуют эту оптимизацию в железе, потому и так мало тактов требуется.

netch80
23.08.2017 15:25C современными возможностями по количеству вентилей вообще умножение строят на сетках и затем параллельных сумматорах… так что обычно не «эта» оптимизация. Хотя результат ещё лучше :)

lieff
23.08.2017 15:48+1Однако блоков умножения у современных процессоров обычно меньше чем ALU, и при out-of-order исполнении давление на эти блоки может оказаться высоким, а ALU блоки простаивать. Так что такие оптимизации все еще могут иметь смысл.
khim
24.08.2017 05:36Не имеют. Архитектура процессоров меняется настолько часто, что вы не успеете программу пересобирать под 100 разных архитектур…

lieff
24.08.2017 13:33Меняются то они часто, но вот принципиально блоков умножения больше чем блоков ALU не становится, т.к. эти блоки дорогие по площади кристалла. Вот например Skylake посмотрите https://en.wikichip.org/wiki/intel/microarchitectures/skylake_(client)#Execution_engine
ALU по прежнему больше и тому объективные причины, а не потому что не хочется.

meta4
22.08.2017 20:42+2Три дереференса + две суммы + одно вычитание + 1 побитовый сдвиг вместо одного умножения? оО

ainoneko
23.08.2017 10:38Там всегда a не меньше b?
Иначе ещё нужна проверка. (Или я чего-то не понимаю?)
alexeymalov
23.08.2017 20:17Программная реализация умножения 8-битных чисел выполняется за пару сотен тактов на z80. умножение с использованием таблиц квадратов — несколько десятков тактов. При частоте процессора в 3,5 MHz ещё как ощутимо
Iqorek
22.08.2017 21:59я вычитал в исходниках Elite для zx spectrum
Где где? Можно ссылку на исходники?Scf
22.08.2017 22:13+8Ну это просто. Загружаешь MONS на 58500, запускаешь его. вбиваешь загрузчик кода Elite, он с адреса 5B00, длину блока указываешь так, чтобы MONS не перетереть. Потом переходишь на 7CB7, это точка входа в игру. И жмешь комбинацию клавиш для показа листинга. Вуаля — на экране исходник.
20 лет прошло, до сих пор помню :-)

netch80
23.08.2017 15:20+1Есть более известный вариант:
ab = (a+b)^2/4 - (a-b)^2/4
только два лукапа по таблице, для a+b и a-b; деление на 4 выполняется нацело, дробные взаимно компенсируются.

shukan
22.08.2017 21:46+1Кто бы еще смог понять, что здесь происходит —
Эвклид без Эвклида ?Понятно, что здесь происходит вычисление обратного числа, Y = X^-1
Но почему именно так? Я хотел было призвать алгоритм Эвклида, но наткнулся на это!
И почему для 64х бит достаточно всего лишь одной лишней итерации?
И что за странный комментарий 3 bits correct? Это потому что odd?
// modular inverse of odd 32-bit value uint32_t modinv32( uint32_t x ) { uint32_t y = x; // 3 bits correct y *= 2 - x * y; // 6 y *= 2 - x * y; // 12 y *= 2 - x * y; // 24 y *= 2 - x * y; // 32 return y; } // modular inverse of odd 64-bit value uint64_t modinv64( uint64_t x ) { uint64_t y = modinv32( (uint32_t) x ); y *= 2 - x * y; return y; }
chersanya
23.08.2017 01:07+3Это не алгоритм Евклида, а существенно более оптимальный, применимый для такого частного случая — получается сложность O(log k) вместо O(k) для Евклида. Переход можно обосновать так: если
y = x^-1 mod 2^k, тоxy = a 2^k + 1; домножим, как в вашей функции, на2 - xy: получимxy * (2 - xy) = (a 2^k + 1) * (2 - a 2^k - 1) = -a^2 2^(2k) + a 2^k - a 2^k + 1 = 1 mod 2^(2k), то есть из обратного к х значения по модулю 2^k получили обратное по модулю 2^(2k). Делая такие переходы как раз из обратного по модулю 2^3 получим по 2^6 и т.д. Также отсюда ясно, почему для перехода к 64 битам достаточно одного шага.
chersanya
23.08.2017 09:22+2А, про первые 3 бита забыл написать. Тут можно очень просто убедиться, перебрав все нечётные числа от 1 до 7 (т.к. рассматриваем обратное по модулю
2^3 = 8) — как видно, каждое число является обратным самому себе. Ну и ещё — к чётным числам обратного ясное дело не существует, поэтому их вообще не рассматриваем.
vlanko
22.08.2017 22:37А в С++ в те времена int уже был 32-битным? Или это не имеет значения для указателей?
tangro Автор
22.08.2017 23:28+1В какие «те»? Quake III Arena, о котором идёт речь в статье, вышел в 1999 году, а int стал 32-битным (сначала это было даже опционально, в зависимости от модели памяти) с распространением 32-битных операционок, т.е. ещё на пару лет раньше.
khim
24.08.2017 05:39Quake III Arena, о котором идёт речь в статье, вышел в 1999 году, а int стал 32-битным (сначала это было даже опционально, в зависимости от модели памяти) с распространением 32-битных операционок, т.е. ещё на пару лет раньше.
Какие, к терапевту, 32-битные операционки? 32-битный int — это Doom, 1993й год.
askv
22.08.2017 23:31А побитовое извлечение корня разве не быстрее? Там только целочисленные операции, без операций с плавающей точкой. Кто-нибудь сравнивал?
mayorovp
23.08.2017 08:39Как вы будете извлекать квадратный корень из числа с плавающей точкой без операций с плавающей точкой?
askv
23.08.2017 22:24Любое число с плавающей точкой f представляется в компе в виде f = z * 2^k. Его всегда легко привести к виду f = z' * 2^(2*k'). Тогда sqrt(f) = sqrt(z') * 2^k'.
z, z', k, k' — целые. Таким образом, вычисление корня из f легко сводится к вычислению корня из целого числа z'.chersanya
24.08.2017 00:01Ну а из целого числа как вы корень извлечёте? И ещё, чтобы такое провернуть нужно отдельно проводить операции над мантиссой и экспонентой, а процессоры хуже работают с числами нестандартного размера, да ещё и не выровненными.
askv
24.08.2017 06:27-2Из целого числа есть поразрядный алгоритм, наподобие умножения столбиком. В десятичной системе он сложный, после адаптации к двоичной превращается в двоичные побитовые сдвиги и сравнения. Погуглите «вычисление квадратного корня столбиком». Например, dxdy.ru/topic24572.html только нужно алгоритм из десятичной системы перевести в двоичную, он сильно упрощается.
Причём тут невыровненные числа? В отдельные переменные (регистры) выделяется мантисса и экспонента, затем с каждыми из них операции ведутся как с обычными машинными словами. После вычислений float/double собирается обратно побитовыми операциями.
bopoh13
24.08.2017 15:20-2Если квадратный корень — целое число, то он является суммой нечетных чисел от 1 до 2n-1 (добавляем 2 порядка, от полученного значения убираем 1 порядок). Замерял скорость на скриптовых языках. Не впечатлён. Для C/C++ алгоритмов много.

Keroro
23.08.2017 06:26Для вычисления целочисленных корней на 8 бит PIC микроконтроллере давно использую Hardware algorithm [GLS] из hackersdelight. Очень компактный и шустрый.
askv
23.08.2017 06:37Есть ещё целочисленный алгоритм, там только побитовые сдвиги и сравнения, нет умножений. Когда-то писал на ассемблере, но листочек затерялся, не могу найти. Но можно попробовать воспроизвести.


spmbt
> 0x5f3759df (это название статьи)
Содержание — супер.
… А в плане SEO название статьи — предельно неудачное: ) Когда клоны наедятся — стоит переименовать. Может, так и было задумано?
tangro Автор
Это название оригинальной статьи. Ради какого-то там SEO портить авторскую задумку — несправедливо.
spmbt
Но SEO в данном случае я видел «в благородном смысле» — ради пользования. Читатель ни за что не запомнит название статьи и не введёт в поиск. Значит, возможность SEO для него пропала. Если бы статья называлась "Быстрый алгоритм квадратного корня и 0x5f3759df" — не пострадали бы ни поиск, ни задумка автора.
(Или, хуже вариант — «Зачем 0x5f3759df для квадратного корня»)
RadicalDreamer
Поисковый запрос вроде «магическая константа обратный корень» вполне себе нормально гуглится.