
Лобовым решением было бы использовать генератор случайных чисел и перед закраской каждого пикселя проверять, не закрашен ли он до сих пор. Это было бы крайне неэффективно: к тому моменту, когда на экране остаётся последний незакрашенный пиксель, потребуется порядка 320?200 вызовов ГСЧ, чтобы в него «попасть». (Вспомним, что Wolfenstein 3D работал на 286 с частотой 12МГц!) Другим лобовым решением было бы составить список из всех 320?200 возможных координат, перетасовать его (можно даже заранее, и вставить в код уже перетасованным), и закрашивать пиксели по списку; но для этого понадобилось бы как минимум 320?200?2 = 125КБ памяти — пятая часть всей памяти компьютера! (Помните ведь, что 640КБ должно было хватить любому?)
Вот как на самом деле реализована эта попиксельная заливка: (код немного упрощён по сравнению с оригиналом)
boolean FizzleFade(unsigned width, unsigned height)
{
unsigned x, y;
long rndval = 1;
do // while (1)
{
// seperate random value into x/y pair
asm mov ax, [WORD PTR rndval]
asm mov dx, [WORD PTR rndval+2]
asm mov bx, ax
asm dec bl
asm mov [BYTE PTR y], bl // low 8 bits - 1 = y xoordinate
asm mov bx, ax
asm mov cx, dx
asm mov [BYTE PTR x], ah // next 9 bits = x xoordinate
asm mov [BYTE PTR x+1], dl
// advance to next random element
asm shr dx, 1
asm rcr ax, 1
asm jnc noxor
asm xor dx, 0x0001
asm xor ax, 0x2000
noxor:
asm mov [WORD PTR rndval], ax
asm mov [WORD PTR rndval+2], dx
if (x>width || y>height)
continue;
// copy one pixel into (x, y)
if (rndval == 1) // entire sequence has been completed
return false ;
} while (1);
}
Что за чертовщина здесь происходит?
Для тех, кому тяжело разбираться в ассемблерном коде для 8086 — вот эквивалентный код на чистом Си:
void FizzleFade(unsigned width, unsigned height)
{
unsigned x, y;
long rndval = 1;
do {
y = (rndval & 0x000FF) - 1; // младшие 8 бит - 1 = координата y
x = (rndval & 0x1FF00) >> 8; // следующие 9 bits = координата x
unsigned lsb = rndval & 1; // младший бит потеряется при сдвиге
rndval >>= 1;
if (lsb) // если выдвинутый бит = 0, то не надо xor
rndval ^= 0x00012000;
if (x<=width && y<=height)
copy_pixel_into(x, y);
} while (rndval != 1);
}
Проще говоря:
rndvalначинается с 1;- каждый раз разделяем значение
rndvalна координаты x и y, и закрашиваем пиксель с этими координатами; - каждый раз сдвигаем и xor-им
rndvalс непонятной «магической константой»; - когда
rndvalкаким-то образом снова примет значение 1 — готово, весь экран залит.
Эта «магия» называется регистр сдвига с линейной обратной связью: для генерации каждого следующего значения мы выдвигаем один бит вправо, и вдвигаем слева новый бит, который получается как результат xor. Например, четырёхбитный РСЛОС с «отводами» на нулевом и втором битах, xor которых задаёт вдвигаемый слева бит, выглядит так:
Если взять начальное значение 1, то этот РСЛОС генерирует пять других значений, а потом зацикливается: 0001 > 1000 > 0100 > 1010 > 0101 > 0010 > 0001 (подчёркнуты биты, используемые для xor). Если взять начальное значение, не участвующее в этом цикле, то получится другой цикл: например, 0011 > 1001 > 1100 > 1110 > 1111 > 0111 > 0011. Легко проверить, что три четырёхбитных значения, не попавшие ни в один из этих двух циклов, образуют третий цикл. Нулевое значение всегда переходит само в себя, поэтому оно не рассматривается в числе возможных.
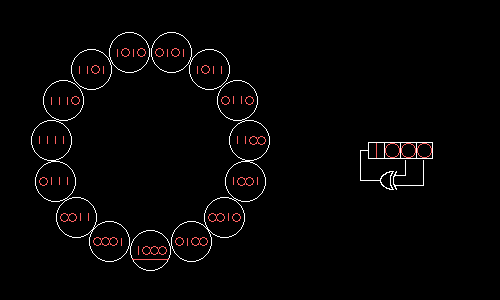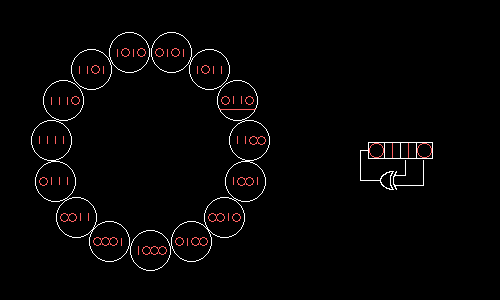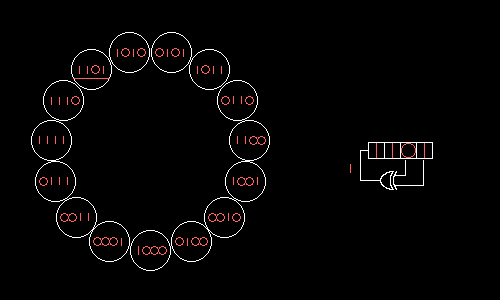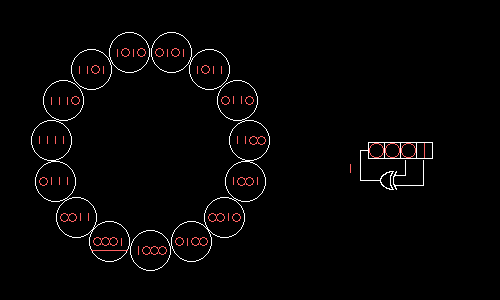
А можно ли подобрать отводы РСЛОС так, чтобы все возможные значения образовали один большой цикл? Да, если в поле по модулю 2 разложить на множители многочлен xN+1, где N=2m–1 — длина получающегося цикла. Опуская хардкорную математику, покажем, как четырёхбитный РСЛОС с отводами на нулевом и первом битах будет поочерёдно принимать все 15 возможных значений:
Wolfenstein 3D использует 17-битный РСЛОС с отводами на нулевом и третьем битах. Этот РСЛОС можно было бы реализовать «в лоб» за семь логических операций:
unsigned new_bit = (rndval & 1) ^ (rndval>>3 & 1);
rndval >>= 1;
rndval |= (new_bit << 16);
Такая реализация называется «конфигурацией Фибоначчи». Равнозначная ей «конфигурация Галуа» позволяет выполнить всё то же самое за три логические операции:
a > b > c > d > e > f > g > h > i > j > k > l > m > n > o > p > q ^ Фибоначчи v v ·< < < < < < < < < < < < < < < < < < < < < < < < < <^< < < < < <· o > p > q>^>a > b > c > d > e > f > g > h > i > j > k > l > m > n ^ ^ Галуа v ·< < < < <·< < < < < < < < < < < < < < < < < < < < < < < < < < <·
- сдвигаем значение вправо;
- копируем выдвинутый бит (n) в самую старшую позицию;
- xor-им этот бит с 13-тым (q).
Если заметить, что старший бит после сдвига гарантированно нулевой, то копирование и xor можно объединить в одну операцию:
unsigned lsb = rndval & 1;
rndval >>= 1;
if (lsb)
rndval ^= 0x00012000;
Значение в «конфигурации Галуа» по сравнению с «конфигурацией Фибоначчи» циклически сдвинуто на три бита: начальному значению 1 в конфигурации Галуа (используемому в коде Wolfenstein 3D) соответствует начальное значение 8 в конфигурации Фибоначчи. Вторым значением РСЛОС будет 0x12000, соответствующее 0x10004 в конфигурации Фибоначчи, и так далее. Если одна из последовательностей принимает все возможные (ненулевые) значения — значит, и вторая тоже принимает все эти значения, хоть и в другом порядке. Из-за того, что нулевое значение для РСЛОС недостижимо, из значения координаты y в коде вычитается единица — иначе пиксель (0,0) так никогда бы и не закрасился.
В заключение автор оригинальной статьи упоминает, что из 217–1 = 131071 значений, генерируемых этим РСЛОС, используются только 320?200 = 64000, т.е. чуть меньше половины; каждое второе генерируемое значение отбрасывается, т.е. генератор работает в половину доступной скорости. Для нужд Wolfenstein 3D хватило бы и 16-битного РСЛОС, и тогда не пришлось бы заморачиваться с обработкой 32-битного
rndval на 16-битном процессоре. Автор предполагает, что программисты id Software просто не смогли найти подходящую комбинацию «отводов», которая давала бы максимальный 16-битный цикл. Мне же кажется, что он сильно их недооценивает :-) Дело в том, что для разделения 16-битного значения на координаты x и y его пришлось бы делить с остатком на 320 или на 200, и затраты на такую операцию деления с лихвой бы скомпенсировали всё ускорение от перехода на 16-битный РСЛОС. Комментарии (92)

bvdmitri
04.09.2017 09:30Объясните пожалуйста, почему нельзя сделать циклы 0..width 0..height? В чем смысл рендерить картинку в случайном порядке (wolfenstein 3D же наверняка не использовала видеоускорители).

tyomitch Автор
04.09.2017 09:45+3Получился довольно зрелищный видеоэффект, который как раз-таки тяжело воспроизвести при использовании видеоускорителей, так что в ремейках Wolfenstein 3D для современных компьютеров вместо FizzleFade использовалось просто постепенное покраснение экрана.

AllexIn
04.09.2017 10:37+5Нет никаких проблем воспроизвести этот эффект на современных видео ускорителях.
Решение в лоб:
текстура, каждый пиксель имеет свое значение от 0 до width*height.
В шейдер передаем счетчик и если значение у пикселя меньше счетчика — закращиваем его красным.
Voila
betauser
04.09.2017 17:15-2Для «современных» того времени. О шейдерах тогда только б-г размышлял)

AllexIn
04.09.2017 17:55+1«Того» времени — это какого?
Во времена Wolfenstein 3D не было никаких видеоускорителей у игроков.
Значит «то время» — это позже…
Во времена ремейков. Ремейки начали появляться почти сразу после релиза, так что не понятно. Про 3dfx я ничего не знаю. Но положим мы говорим про ускорители с поддержкой OpenGL.
glReadPixels есть начиная с OpenGL 1.0
Значит читаем буффер цвета через glReadPixels, а потом каждый кадр заливаем несколько пикселей красным и запихиваем это в текстуру, показываем на экран. Ну и далее по тексту.
С производительностью проблем не будет, потому что мы вообще ничего не делаем в кадре кроме запихивания текстуры в видео память и отображения её одним дипом.
Вообще, ИМХО, ремейки не стали повторять этот эффект не потому, что не могут. А потому что он при нормальном разрешении смотрится гораздо хуже.
tyomitch Автор
04.09.2017 18:09+11) Ремейки начали появляться после 1995, когда id выложила исходники в паблик, и разрешила их использовать и модифицировать.
2) Что именно смотрится хуже? Если пиксели стали слишком мелкие, можно тем же самым кодом заливать экран маленькими квадратиками или любыми другими фигурками.

da-nie
06.09.2017 20:23Значит читаем буффер цвета через glReadPixels,
К сожалению, это очень тормознутая функция (например, на многих видеокартах ATI годов эдак около 2005-2007). Я эту функцию использовал для моделирования отражённого сигнала от оптодатчика и тут-то и выяснилось, что на картах ATI она жутко тормозит (раз в 10 по сравнению с nVidia).
AllexIn
06.09.2017 20:30К сожалению, я не могу вернуться в 1995 год, чтобы проверить.
А искать раритетную видуху того времени и писать тест, как-то не входит в сферу моих интересов.
Так что спорить не буду.
da-nie
06.09.2017 20:53Только год был 2005. :) А может, и сейчас тоже тормоза будут на каких-то видеокартах. Вы можете это проверить. Я вам могу дать программу для тестирования. :) Ту, для которой я это и использовал.
Вот.
Там нажмите «выполнить задание» и выберите rotate.txt. Если каждый кадр станет замирать на несколько секунд (и десятки секунд) — ваша карта тормознутая. У меня где-то FPS около 3-4 на nVidia 450 и задание выполнено за 9 секунд примерно.
AllexIn
06.09.2017 21:31Я с 2005 года в графике.
Всегда сохранение скриншотов делали через glReadPixels.
Даже в те времена эта операция легко давала десятки FPS.
Может быть вы напоролись на кривые драйвера…
da-nie
06.09.2017 21:48Десятки? Нет, мне не десятки нужны были. :) Вот в этой программе, что я привёл, на одну точку ротора снимается 128 снимков для каждого датчика (а их 6). Итого, 768 кадров.
Вряд ли драйвера виноваты — я опробовал около десятка разных видеокарт и на разных компьютерах. У ATI эта функция существенно тормозила — тут обработку смело можно было оставлять на ночь. :)
AllexIn
06.09.2017 21:50Ну glReadPixels с 1000 FPS — это сильно за рамками алгоритма что я выше писал. :)
Ему 20 выше крыши…
da-nie
06.09.2017 22:15Ну, я писал про то, что на разных картах эта функция может быть тормознутой. А вот насколько она окажется тормознутой на конкретной — не угадать. Может оказаться, что на каких-то картах и 20 FPS не получить — ну а вдруг.

AllexIn
06.09.2017 22:21Ну я лишь хотел сказать, что утверждение «сложно реализуется при использовании видеоускорителей» не верно. Конкретные реализации — воспро второй. Их много и надо смотреть от конкретных условий.
P.S.
Кстати, я уж и забыл с чего всё началось. Нам надо glReadPixels сделать только один раз, а не 20 раз в секунду. Чтобы получить актуальный кадр. Дальше просто в памяти закрашиваем и отправляем на рендер.

gurux13
04.09.2017 09:31Из минусов этого подхода — экран всегда закрашивается одинаково. Хотя это и выглядит как рандомная закраска.
Ghost_nsk
04.09.2017 09:46+3Можно использовать другое начальное значение (из той же последовательности), последовательность останется та же, но сместится, и эффект повторения будет менее заметным.

tyomitch Автор
04.09.2017 09:53+6С точки зрения программистов Wolfenstein 3D, предсказуемость — это как раз плюс :)
Даже для основного ГСЧ использовалась таблица заранее перетасованных значений, выдающая одну и ту же псевдослучайную последовательность при каждом запуске.
Позже, во времена DOOM и сетевой игры, стало критически важным, чтобы у всех игроков ГСЧ генерировал в точности одну и ту же последовательность значений, потому что по сети передавались только нажатия на клавиши, а обрабатывал их каждый компьютер сам по себе.

SL_RU
04.09.2017 11:15+6Не вижу в таком решении магии — каждый студент, с пользой отсидевший курс цифровой электроники, при слове «случайное число» вспомнит именно это применение сдвигового регистра(сразу пришло на ум именно это). А уж посчитать свою зависимость и воплотить это в коде не составит проблем.

Loiqig
04.09.2017 12:31+2Пожалуй да, я то же об этом сразу подумал. Но не каждый студент отсидевший курс цифровой электроники позже занялся программированием, некоторые всё же по прямому назначению данный курс применяют — проектируют цифровую электронику. Ещё, хотелось бы, может быть больше математики в доступной форме, а то инженерное решение есть, а как в теории это получается маловато.

Labunsky
04.09.2017 19:32+1Программисты должны были регистры сдвига застать на курсе случайных генераторов)

MacIn
05.09.2017 12:31+1Где как. У нас про собственно сдвиг речь шла только при изучении языка ассемблера x86, про сдвиговые регистры — на «организации ЭВМ», «архитектуре ЭВМ». Как таковая тема ГПСЧ не присутствовала.

eaa123
04.09.2017 11:49По мне так лобовое решение это ГПСЧ основаный на конгруэнтном методе!

tyomitch Автор
04.09.2017 11:55+6А теперь сравните: ЛКМ; РСЛОС.
В первом случае «неслучайность» заливки видна невооружённым взглядом (горизонтальные полоски и фигуры).
eaa123
04.09.2017 12:50Несомненно, ЛКМ не лучший вариант (хотя правильно подобрав параметры можно свести на нет визуальные артефакты), речь о другом, метод монте-карло, который заявлен как лобовой, стоит применять только в исключительных случаях, например когда присутствуют достаточно сложные ограничения на случайную величину.

MacIn
04.09.2017 12:23Здорово, отличная идея, спасибо за статью.
В лоб пришло бы на ум все же использовать монте-карло — ГПСЧ с постепенным увеличением кол-ва генерируемых пар. Но это даже без прикидок очевидно слишком затратное по ресурсам решение.

thebmv
04.09.2017 16:41А в каком месте там 125 Кб получается? Мне видится битовая маска закрашен/не закрашен всего около 8 Кб.

tyomitch Автор
04.09.2017 16:43+1125КБ нужны для перетасованного списка координат:
Другим лобовым решением было бы составить список из всех 320?200 возможных координат, перетасовать его (можно даже заранее, и вставить в код уже перетасованным), и закрашивать пиксели по списку

betauser
04.09.2017 17:09precompiled tiled random template:
15 2 14 13
11 6 7 8
9 16 5 12
4 3 1 10
tyomitch Автор
04.09.2017 17:27Что это, откуда оно, и зачем?

betauser
04.09.2017 17:40Выбираем размер массива (в примере 4x4). Прекомпилируем рандомно цифры. Сохраняем в массив. Далее последовательно выбираем и получаем координаты. Тайлим на весь экран.
© сам придумал :)
betauser
04.09.2017 17:44Для данной задачи, скорее всего, было бы достаточно 32x32. По два байта на координату (X, Y). Получается массив будет 2048 байт.

betauser
04.09.2017 17:54Типа как noise текстура, вместо пикселей — уникальные координаты.


MacIn
05.09.2017 12:36Можно и не так — просто заранее создать битовую маску закраски. 320/8 = 40; 40*200 ~~ 8Кб. Маска создается с определенными условиями — скажем, в старших 4 и младших 4 битах должно быть от 1 до 2 единиц. Потом закрашиваем экран последовательно 3 раза подряд, каждый раз сдвигая эти маски. Если единица была в крайнем левом разряде, то к 3й закраске она будет в крайней правой позиции, что гарантированно закрасит все пиксели. А уж то, что некоторые закрасятся по нескольку раз — не имеет значения. Хотя, в принципе, это не сильно будет отличаться от предложенного метода со сдвиговым регистром, не считая заранее подготовленных данных. Но просто, как вариант навскидку, если неизвестно свойство сдвигового регистра с ОС генерировать последовательность по кругу.

betauser
05.09.2017 16:28Вот сейчас любопытно стало, чтобы еще и саму текстуру процедурно генерировать. Т.е. получается два этапа:
1. Генерация такой текстуры с уникальными, хорошо разложенными координатами. В итоге, получаем массив.
2. Собственно, использование массива для задачи.
Такой подход даст максимальный перформанс и при этом не нужно было бы тратить место для хранения массива, если он большой.
Для первой задачи нужен какой-то алгоритм с генерацией уникальных координат. При этом, чтобы при любых входных данных получалось бы красивое рандомное распределение. Входные данные: размер массива, т.е. два числа X, Y.
Частности — квадратный или прямоугольный.

valentin78
04.09.2017 17:27когда мне задали такую задачку, по принципу — а как бы ты сделал, мне пришла идея, как мне кажется куда проще, — если представить экран Х на Y в виде одномерного массива (по сути это и есть кусок видео памяти), то зная что всего Z = x * Y точек, мы генерируем случайное числ от 0 до Z — 1 = A и начинаем бегать по массиву (видеопамяти) и искать не закрашенную точку, при этом если нашли такую считаем сколько раз, пока не получим число = A, и красим ее
далее Z = Z — 1 и повторяем процедуру
недостаток только в том что нам нужно каждый раз читать видеопамять на предмет не закрашенной точки N раз, где N [1… W*H]
tyomitch Автор
04.09.2017 17:33+1Это ничем не отличается от описанного мной лобового подхода:
Лобовым решением было бы использовать генератор случайных чисел и перед закраской каждого пикселя проверять, не закрашен ли он до сих пор. Это было бы крайне неэффективно: к тому моменту, когда на экране остаётся последний незакрашенный пиксель, потребуется порядка 320?200 вызовов ГСЧ, чтобы в него «попасть».
—точно так же, для закраски последней точки потребуется порядка 320?200 операций, а на всю заливку целиком — порядка (320?200)? операций, т.е. несколько минут на 286-12МГц.
Пользователь раньше заснёт со скуки, чем такая заливка завершится.
valentin78
04.09.2017 18:22еще как отлчается
это не тупой перебор точек на предмет закрашено или нет
а ровно X * Y случайных чисел, т.е 320?200 операций, не более
хотя смотря что вы понимаете под операцией
пример:
2 х 2
случайное число
2 (0..3) — красим x=0, y=1
2 (0..2) — красим x=1, y=1 (пропускаем x=0, y=1 т.к. оно уже закрашено)
0 (0..1) — красим x=0, y=0
0 (0..0) — красим x=1, y=1 (опять же, первый закрашен, пропускаем)
итого 4 операции, и не 16
tyomitch Автор
04.09.2017 18:28Перед закраской последнего пикселя на экране 63999 закрашенных пикселей и один незакрашенный.
Сколько операций потребуется, чтобы найти незакрашенный?
valentin78
04.09.2017 18:34от 1 до 63999

TheShock
04.09.2017 18:38+2Ну то есть квадратическая сложность вместо необходимой линейной, о чем tyomitch и ведет речь.

valentin78
04.09.2017 18:43он говорит об «порядка (320?200)? операций»
в моем случае их в 2 раза меньше, как сумма 1..n, где n = 320х200
я уже не помню как посчитать такты, забылось, но мне кажется что на ассемблере при прямой работе с видеопамятью, не так страшен черт
TheShock
04.09.2017 18:49+3порядка (320?200)? операций = 4 096 000 000
в два раза меньше = 2 048 000 000
т.е. это тот же порядок и он совершенно прав. Тем более атомарных операций может быть даже больше (как минимум — рассчет позиции в массиве, получение значения, сравнение с необходимым и увеличение счетчика для каждого пикселя), так что операций будет даже больше, чем он сказал, но порядок указан правильно: сложность квадратическая, операций миллиарды, а должна быть линейной, операций должно быть десятки тысяч.
valentin78
04.09.2017 18:53в целом соглашусь
вот только если просто последовательно закрашивать экран 320 х 200 сплошным текстом, то это уже будут сотни тысяч операций, ни как не десятки
TheShock
04.09.2017 18:56+2Согласен. Сотни тысяч. Может даже миллионы? Но не миллиарды (в 1000-10000 раз меньше), а это значит, что отработает за 100 миллисекунд, а не за 100 секунд.
Главное, что количество операций должно быть линейно от количества пикселей (оптимизация константы — менее важный вопрос).

zoas
05.09.2017 12:33Делаем более линейной с некоторой правкой алгоритма: если пиксель уже закрашен, красим первый незакрашеный пиксель справа (или слева).

beeruser
05.09.2017 03:41мне пришла идея, как мне кажется куда проще
Вместо простой установки пикселя по RND, вы собрались генерить RND и ещё что-то там сканировать? В чём простота?
нужно каждый раз читать видеопамять
IBM VGA takes an average of 1.1 microseconds to complete each memory read (единственная цифра которую я нашел)
Получаем ~900кБ(скорость чтения байт в сек)/64кБ(размер фреймбуфера) = 14 (чтений всего экрана в секунду)

jumpordie
04.09.2017 18:46-4Не очень понимаю весь ажиотаж вокруг таких тем. Подобные трюки с разной степенью "извращенности" использовались на спектрумах и коммодорах задолго до пришествия id. Помню на спектруме, чтобы не проверять все ли пиксели перекрасились, попросту после определенного количества циклов все байты в экранной области заполнялись #FFами..

BratSinot
04.09.2017 19:11+3Так статьи про «Подобные трюки с разной степенью „извращенности“» тут пишут не только про iD. Про NES, Atari и еще других было.

fukkit
04.09.2017 20:08-2Алгоритм — ок, эффект — сомнительный. Кровь так себя ни разу не ведёт. Математик укусил дизайнера или за 10 минут на спор сделали?
P.S.: игрушка культовая конечно была.
McAaron
05.09.2017 00:57-2Для этой цели подойдет любой простейший генератор псевдослучайных чисел с достаточным периодом. Например, линейный конгруэнтный.

alexback
05.09.2017 09:39+4Просто раньше программисты были настоящими математиками, такими, что большинству нынешних остается только читать такие статьи с широко открытыми глазами.

Muzzy0
05.09.2017 13:19-2Чтобы знать, какой пиксел уже закрашен, а какой — нет, нужен 1 бит на пиксел. Итого, 1 байт на 8 пиксел:
320 * 200 /8 = 8 000 байт, чуть меньше 8 килобайт. Немало, но совсем не 125 килобайт, в 16 раз меньше.Ghost_nsk
05.09.2017 15:00+1Не нужно знать какой уже закрашен, достаточно знать что в итоге закрасятся все, без повторов.

kdekaluga
05.09.2017 20:13+1Прочитал первые пару абзацев, думал около трех минут и пришел к такому же решению) Первоначально хотел составить динамический список (std::list) из пикселей, но в нем нельзя обращаться к произвольному элементу быстро. Затем была мысль AVL дерева из всех пикселей, в котором на каждом шаге мы случайным образом определяем, перейти влево или вправо или же остановиться на текущем элементе (думаю, поход дал бы приемлемый результат, памяти бы выделить пришлось, но только на время алгоритма), ну а потом вспомнил про ГПСЧ на сдвиговых регистрах.
На самом деле это как бы счетчик, проходящий все 2^N состояний, просто не последовательно. В плис, кстати, это самый простой вариант реализации счетчиков любой длины. Сам использую такие на МК Atmel — если сохранять значение при выключении прибора в EEPROM, а при включении загружать оттуда, получается почти random.
Все же ограниченная производительность способствует поиску интересных решений)Ghost_nsk
06.09.2017 06:24Для перебора всех 2^N состояний нужно правильно выбрать полином, но это уже нюансы реализации.

MacIn
06.09.2017 12:39+1Первоначально хотел составить динамический список (std::list) из пикселей, но в нем нельзя обращаться к произвольному элементу быстро. Затем была мысль AVL дерева из всех пикселей,
Сколько памяти потребуется на хранение этих структур данных?
kdekaluga
06.09.2017 19:55Список отпадает по причине медленного доступа, а вот вариант с AVL давайте рассмотрим. Каждый элемент дерева должен хранить:
— Х-координату (9 бит)
— Y-координату (8 бит)
— «указатели» на левую и правую ветвь (достаточно по 16 бит)
— флаг состояния вершины дерева (2 бита)
Итого, 8+9+2*16+2 = 51 бит на элемент. Т.е. 7 байт. Всего 320*200*7 = 448000 = 437.5 Кб. Немало, но в 640 влезает. На момент гибели игрока в игре можно пожертвовать текстурами/какими-либо еще данными, которые потом загрузить с диска, чтобы освободить данный объем памяти. Вариант, конечно, не лучший, но реализуемый (ну, и на 286 обычно был 1 Мб).
MacIn
06.09.2017 20:27+1— Х-координату (9 бит)
Если не гнаться за чистотой, можно и 8 обойтись. Считаем, что экран — 256 пикселей и делаем свертку, дублируя левую часть справа.
Тут еще выравнивание будет хромать, если по 7 байт на элемент взять. Да и если обрезать указатель до 16 бит, надо как раз выравнивать так, чтобы справа были «мнимые нули» в адресе.
Немало, но в 640 влезает. На момент гибели игрока в игре можно пожертвовать текстурами/какими-либо еще данными, которые потом загрузить с диска, чтобы освободить данный объем памяти. Вариант, конечно, не лучший, но реализуемый (ну, и на 286 обычно был 1 Мб).
Если мы хотим уложиться в 640к, то 437 не влезет никак, слишком много там данных системы, драйверов, утилит. А так эта игра работала емнип работала и с памятью свыше 1 Мб, так что все равно не так критично. Хотя это и будет забивание гвоздей микроскопом по сравнению со сдвиговым регистром.
kdekaluga
06.09.2017 20:46Тут еще выравнивание будет хромать, если по 7 байт на элемент взять
Выравнивание на 286? :) Ну, может быть будет медленнее такта на 3)
Да и если обрезать указатель до 16 бит
Зачем? Я специально написал указатель в кавычках — это может быть просто индекс от массива с размером элемента 7 байт. Таких элементов будет 64000, т.е. как раз укладываемся в 16 бит. Ну а чтобы получить реальный адрес, надо будет умножить на 7 (или умножить на 8 и вычесть 1).
Если мы хотим уложиться в 640к, то 437 не влезет никак,
Насколько я помню, при правильном подходе было >500К свободной основной памяти, т.к. когда её становилось меньше, начинались проблемы с играми и некоторыми программами.
Конечно, писать такой мелкий эффект на такой объем памяти никто в здравом уме не станет, но мы же рассматриваем лишь теоретическую часть вопроса.
MacIn
07.09.2017 13:26Выравнивание на 286? :) Ну, может быть будет медленнее такта на 3)
Копейка рубль бережет :P
Зачем? Я специально написал указатель в кавычках — это может быть просто индекс от массива с размером элемента 7 байт. Таких элементов будет 64000, т.е. как раз укладываемся в 16 бит. Ну а чтобы получить реальный адрес, надо будет умножить на 7 (или умножить на 8 и вычесть 1).
Умножить на 8 и вычесть единицу это не умножить на 7 же. 100*7 <> 100*8 — 1. Вычесть нужно индекс, т.е. 100*8 — 100. Если указатель выровнен, то это будет просто умножение, т.е. сдвиг. Все как всегда — скорость vs память.
Я запамятовал, как будет адресоваться память в этом случае — сегментами или одним куском? Если сегментами, то мы еще попадем на расщепление линейного адреса; последний элемент будет размазан между двумя сегментами; арифметические операции придется делать на двух регистрах. Думаю, слишком много накладных расходов.
kdekaluga
08.09.2017 01:29Копейка рубль бережет :P
«Если каждый месяц откладывать немного денег, то уже через год вы увидите, как мало у вас набралось» :)
Судя по гифке, эффект отрабатывает примерно 10К точек в секунду — больше не надо, иначе он потеряет смысл. Это дает примерно 1200 тактов на точку при тактовой частоте 12 МГц. Немного, но и не так уж мало. Если и возникнет проблема с такой реализацией, так это из-за того, что в AVL дереве операция удаления элемента занимает до Log2(N) итераций, т.е. до 16 в нашем случае. Плюс еще нужен ГПСЧ, чтобы определять, где остановиться.
Вычесть нужно индекс, т.е. 100*8 — 100
Это и имелось в виду)
Я запамятовал, как будет адресоваться память в этом случае — сегментами или одним куском?
Сегментами. Но в реальном режиме адрес в памяти равен s*16 + D, где S — значение сегментного регистра. Т.е. умножение на 7 надо проводить на 19-ти разрядах, после чего 15 старших отправить в сегментный регистр, а 4 младших — в регистр адреса (типа ВХ). Никаких проблем с выходом за границу сегмента не будет.
tyomitch Автор
08.09.2017 02:29Судя по гифке, эффект отрабатывает примерно 10К точек в секунду — больше не надо, иначе он потеряет смысл.
Не надо судить по гифке, лучше судить по исходникам: весь эффект целиком (64К пикселей) занимает 70 кадров, т.е. ровно секунду (в соответствии с частотой развёртки VGA).
Можно даже воспользоваться эмулятором и перепроверить: да, ровно секунду.

Halt
06.09.2017 08:18+2На правах маразма: если забыть об эффективности, то похожий результат можно достичь, обходя квадрат по кривой Гильберта (или Мура), но не подряд, а с некоторым шагом :)

viiri
06.09.2017 10:09Дело в том, что для разделения 16-битного значения на координаты x и y его пришлось бы делить с остатком на 320 или на 200, и затраты на такую операцию деления с лихвой бы скомпенсировали всё ускорение от перехода на 16-битный РСЛОС.
В случае с VGA-режимом 13h (с линейной организацией видеопамяти) можно и не делить. 16-битное число можно использовать в качестве индекса в сегменте 0xA000 для записи пикселей в видеобуфер. Но Кармак использовал планарный VGA-режим и, возможно, счёл, что проще использовать 17-битный РСЛОС и использовать уже написанную функцию быстрого вывода пикселей (функция использует битовый сдвиг и таблицу поиска ylookup для вычисления смещения начала строки), чем городить огород.
tyomitch Автор
06.09.2017 10:21В жж комментируют:
VGA-адаптер зачастую имел больше 64KB памяти, но в линейном режиме они были недоступны. В планарных режимах (mode X) этого ограничения не было и можно было использовать несколько страниц видеопамяти для дешёвой организации двойной (и даже тройной) буферизации, но при этом возникали «лишние трудности» при расчёте адресов и переключении плоскостей вывода.

tyomitch Автор
06.09.2017 18:18Ну и добавлю сюда свой ответ из жж: разделять
rndvalна координаты пришлось бы в любом случае, поскольку в действительности закрашивается не весь экран целиком, а только viewport; рамка вокруг него (чем меньше viewport, тем быстрее работает игра) и статусбар внизу экрана остаются незакрашенными. Вот для этого клиппинга и нужна проверка координат по отдельности.


kdekaluga
06.09.2017 20:13Разделить — это не так уж долго. На 286-м команда деления выполняется за 14 (вариант 16/8 = 8 + 8 битов) и 22 (32/16 = 16 + 16) такта. Не очень много по меркам того времени (среднее время выполнения обычной команды на 286: 2-3 такта). Не думаю, что именно это стало причиной выбора 17-битного решения.


lucius
Помню, когда учился программировать на Паскале, столкнулся с задачей попиксельного закрашивания экрана. Решал тогда не таким изящным методом, но тоже работал:
1) Массивы индексов перешивал, меняя местами пары элементов;
2) Закрашивал экран попиксельно, двигаясь по перемешанным массивам.
NeonMercury
Цитата из статьи для Вас:
lucius
Спасибо за цитату, перечитал еще раз, но мне не требовалось хранить такой большой массив, потому что достаточно было хранить 2 перемешанных массива, один из которых содержал 320 элементов, другой 200. (320+200)*2 = 1КБ, что не так уж и много. К тому же перемешивать каждый из небольших массивов можно очень быстро.
tyomitch Автор
Поясните, пожалуйста, как вы из этих двух перемешанных массивов получите последовательность из 64000 пар координат.
На всякий случай напомню, что НОК(320,200) = 1600
Aivean
Наверное, как-то так.
Правда, только двумя массивами, без битовой магии, вроде той, что описана в статье, вряд ли получится добиться однородного распределения. А вот четырьмя (как в моей демке), получается неплохо.
YNechaev
С квадратом получилось бы неплохо — достаточно бегать по обоим массивам и после каждого прогона циклически сдвигать один из них на один элемент. С произвольной областью можно сделать два массива по 320 и отбрасывать всё что за границей экрана.
tyomitch Автор
Вот вариант с циклическим сдвигом и «истинно случайными» перетасовками от www.random.org/sequences — к сожалению, в такой заливке видны регулярные артефакты.
fasterthanspeed
На самом деле можно пофиксить заменой
siнаyy[si - 1]: http://jsfiddle.net/4gxgy07a/ и будет норм =).TheShock
Прекрасно! А в чем магия?
Aivean
Не обязательно 320x200 хранить. Достаточно 320x4: вот, набросал на скорую руку демку.
tyomitch Автор
Красиво получается! Но лобовым решением это уже не назвать :)
Nefrace
Ну, как уже было написано в статье — держать в памяти весь массив пикселей было, мягко говоря, затратно.