В этом посте я представлю вам пример мыслительного процесса от задачи к ee алгоритмическому решению.
Должен признаться, что из-за многолетнего влияния объектно-ориентированной парадигмы на мой мозг, первое, что мне пришло в голову, это для всех сущностей, участников задачи, написать классы. Проблемно-ориентированное программирование и все такое. Но я вовремя остановился, вспомнив старые учебники по паскалю, где оперировали понятиями фунцкия и процедура.
Чтобы перевести задачу в плоскость понятную машине, нам нужно избавиться от тех частей контекста задачи, который не имеет значения для ее решения.
Не имеет значения все, что нельзя выразить числами. Капуста это или мяч не имеет значения, важно, что участников четверо. Река перед ними или гора — неважно, есть два места где могут находиться участники этой задачи. На лодке они переправляются или на самолете — неважно, они могут перемещаться с одной точки в другую и наоборот, при чем в перемещении всегда задействован крестьянин (или «мужик») — особенный участник.
В полной абстракции условия будут выглядеть как-то так:
- Есть набор из трех элементов и один специальный элемент.
- Есть запрещенные комбинации элементов (при отсутствии специального элемента)
- В комбинации со специальным элементом все комбинации допустимы.
- Нужно перенести все элементы с одного места в другое, так чтобы никогда не образовывались запрещенные комбинации элементов.
- При этом переносить можно лишь один элемент, либо в одну, либо в другую сторону, поочередно. Т.е. нельзя сделать два переноса в одну сторону. — спасибо Dr_Dash за то, что заострил на этом внимание.
Чтобы различать элементы и их комбинации, нам нужно дать им идентификаторы. Машина лучше всего работает с числами — обозначим их числами. Мы хотим комбинировать элементы. Комбинировать числа значит делать над ними арифметические операции.
Тогда закодируем отдельные значения так, чтобы сумма чисел однозначно указывала на комбинацию:
0 — никого
1 — P Крестьянин(Peasant)
2 — G Коза (Goat)
4 — C Капуста (Cabbage)
8 — W Волк (Wolf)
Буквы тут только для мнемоники и никакой нагрузки не несут
То, что крестьянин обозначен числом 1 — важно. Изза этого «код конфигурации берега» с крестьянином всегда будет нечетным. Так можно будет понимать на с какой стороны он находится.
Запишем возможные комбинации на обеих берегах в виде таблицы, и отметим допустимые варианты распределения участников по берегам иксом:
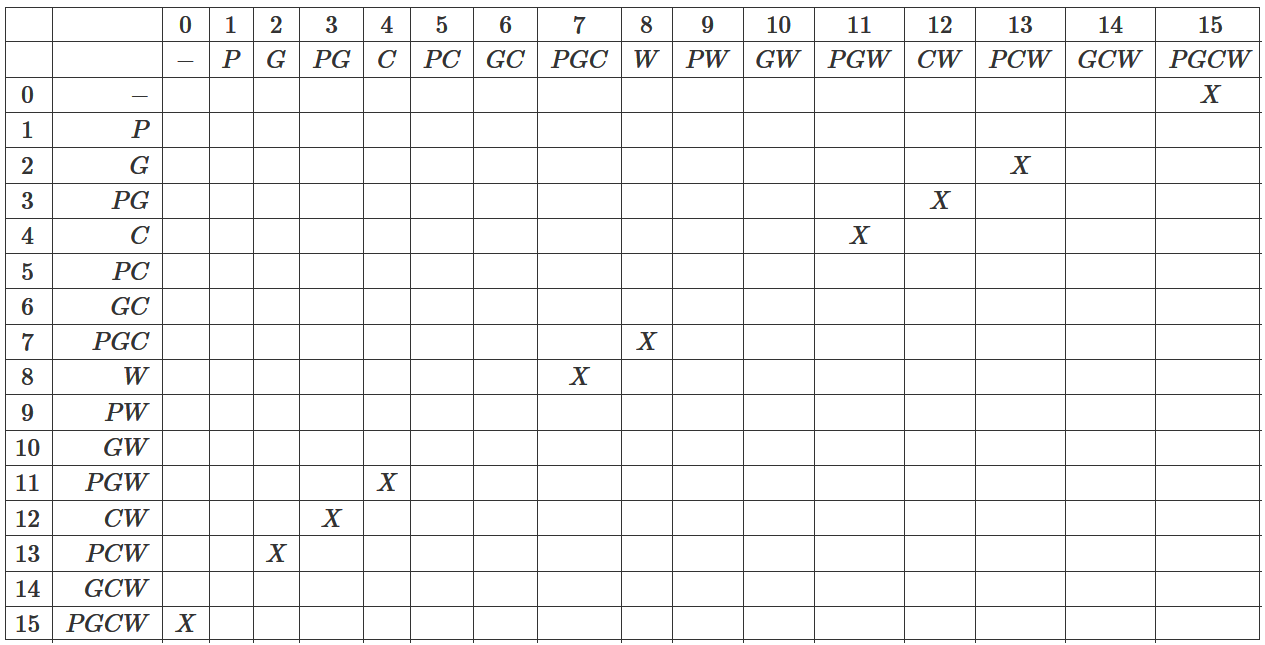
Заметим, что возможные комбинации конфигурации берегов всегда в сумме дают 15, но не все из них допустимы.
Из визуального представления в виде таблицы становится ясно, что нам нужно перейти из одного угла таблицы в другой, переходя при этом только в допустимые состояния.
Какой берег левый, а какой правый, для задачи не имеет значения. Т.е указав код конфигурации например 11, мы говорим, что на одном берегу находятся крестьянин, коза и волк. То, что капуста на другом берегу не нужно особенно указывать. Поскольку в сумме оба берега дают 15, то 4 — капуста, на другом берегу.
Представим себе, что наши состояния это камни в воде, и мы перепрыгивая с камня на камень должны переместиться с одного конца в другой. Напоминает ленту машины Тьюринга, правда?
На ленте начало обозначено черным треугольником справа, а конец — перевернутым треугольником слева. Возможные промежуточные состояния обозначены черными точками. Недопустимые состояния помечены крестиком.
Перемещаться мы можем только в допустимые состояния. Также, из условия задачи известно, что в перемещении всегда участвует крестьянин и, что лодка умещает максимум двоих. Значит, мы можем оперировать числами 1 (крестьянин), 3 (крестьянин и коза), 5 (крестьянин и капуста), 9 (крестьянин и волк).
Получается, если мы начинаем из состояния 15, когда все на одном берегу — единственное из возможных следующих состояний это 12. Из состояния 12 у нас нет другого выхода, кроме как вернуть крестьянина на другой берег, делаем +1. Переходим в состояние 13. Отсюда мы можем сделать либо -5 (перевезти капусту) либо -9 (перевезти волка). Если мы сделаем -9 то попадем в состояние 4, но крестьянина после этого надо вернуть. Одного его мы вернуть не можем, иначе мы окажемся в состоянии 5, но мы можем вернуть его с козой т.е. +3, и окажемся в состоянии 7(коза капуста и крестьянин). Отсюда мы можем сделать либо -3 (эвакуировать козу) либо -5 (спасти капусту). Поскольку -3 было бы откатом предыдущего действия, остается -5. Мы переходим в состояние 2. Отсюда мы можем сделать только +1, и +9 (поскольку +5 было бы откатом предыдущего действия, a +3 недопустимое состояние).
Заметьте, +3 невозможно здесь не потому, что «коза ведь на другом берегу» (это обьяснение понятное человеку), а потому, что это переход в недопустимое состояние («обьяснение» понятное машине). Делаем +1. Переходим в состояние 3. Делаем -3. Готово.
Но это не единственно возможное решение. Заметьте, что человеку трудно отслеживать все перемещения. Для машины же, существует набор допустимых и недопустимых состояний, и набор правил.
Давайте заставим машину найти все возможные решения задачи. T.e. найти все возможные цепочки состояний которые ведут к решению. Воспользуемся рекурсией и питоном в качестве языка.
Для хранения цепочек переходов возьмем массив. Первое состояние в массиве 15. Передадим его в фунцкию рекурсии. Определим условие окончания рекурсии. Это когда конечный элемент цепочки будет 0.
def f(states):
s = states[-1] #состояние рассматриваемое в итерации, последнее в цепочке.
if s==0: # условие остановки
print(str(states))
print("END")
else: # если условие остановки не достигнуто
...
print(f([15]))
Если состояние четное (крестьянин на другом берегу), то мы выполняем одну из возможных операций с положительным знаком (+1, +3, +5 или +9).
Для каждой возможной операции должны выполняться условия:
— она не ведет в недопустимое состояние,
— она не ведет за максимальную положительную границу ленты
— она не ведет в состояние в котором мы уже были.
Если такая операция имеется, выполни ее, и добавь новое состояние к цепочке состояний.
Передай новую цепочку состояний в рекурсивную фунцкию.
if s%2 == 0:
for i in [9,5,3,1]:
if (s+i not in [1,5,6,9,10,14]) and (s+i<=15) and (s+i not in states):
f(states+[s+i])
Если же состояние нечетное, то мы следуем тем же соображениям, но со знаком минус.
else:
for i in [9,5,3,1]:
if (s-i not in [1,5,6,9,10,14]) and (s-i>=0) and (s-i not in states):
f(states+[s-i])
def f(states):
s = states[-1]
if s==0:
print(str(states))
print("END")
else:
if s%2 == 0:
for i in [9,5,3,1]:
if (s+i not in [1,5,6,9,10,14]) and (s+i<=15) and (s+i not in states):
f(states+[s+i])
else:
for i in [9,5,3,1]:
if (s-i not in [1,5,6,9,10,14]) and (s-i>=0) and (s-i not in states):
f(states+[s-i])
print(f([15]))
На выходе получим
[15, 12, 13, 4, 7, 2, 3, 0]
END
[15, 12, 13, 8, 11, 2, 3, 0]
END
None
Заметим, что в решении четные и нечетные числа чередуются. Это перемещения крестьянина с одного берега на другой. Не зря выше мы обозначили его единицей.
Также обратим внимание на то, что изначальные условия задачи, понятные человеку, в программном решении превратились в цифры и операции над ними.
Надеюсь, кому-то эта статья окажется полезной.
P.S.:
Если у кого-то есть обьектно-ориентированное решение, то пожалуйста поделитесь им в комментариях, чтобы можно было сравнить парадигмы.
Комментарии (21)

Dr_Dash
15.10.2017 17:17Я занимался решением этой задачи через автоматы, то есть хотел построить автомат решающий эту задачу для Х коз Y волков Z капуст и K крестьян, и формулируя эту задачу конкретнее, я понял, что по сути это задача-обманка. Просто нужен свежий взгляд. Смотрите о чём я:
Есть два «инертных» элемента — волк и капуста, которые никак не влияют друг на друга, и есть «активный» элемент сродственный обоим элементам, который не должен комбинироваться ни с одним из других. Крестьянина считать элементом комбинации нецелесообразно. Когда крестьянин на берегу мы это не должны считать комбинацией вообще. Комбинация фиксируется только тогда когда крестьянин плывёт по реке, а когда он на берегу, это переход между состояниями. В комбинациях участвуют только те элементы, которые не в лодке.
А теперь представляем себе задачу с начальными условиями «на этом берегу крестьянин, волк и капуста, а на том коза»(получается из нашей задачи предварительной перевозкой козы), и тогда у нас имеется как бы два параллельно протекающих процесса, и даже не связанных по большому счёту:
1 крестьянин перевозит на тот берег волка, возвращается, потом перевозит капусту.
2 на обратном пути между перевозкой волка и капусты, коза переезжает с того берега на этот.
В результате мы имеем на выходе полную симметрию начальному условию: на том берегу волк, капуста и крестьянин, на этом коза. Осталось забрать козу.
При такой формулировке «активный» элемент никогда не входит в комбинацию с «инертными»
Любое увеличение коз, капуст или волков порождает уже другую задачу, не столь элегантную.

lxsmkv Автор
15.10.2017 22:352 на обратном пути между перевозкой волка и капусты, коза переезжает с того берега на этот.
По условиям оригинальной задачи, перемещение возможно только с участием крестьянина. А так получается у нас какая-то квантовая физика уже, коза как бы еще там но уже не там. В классической машине Тъюринга нет неопределенности. Или мы в одном состоянии или в другом. Нет никакого промежуточного состояния. Как и нет процесса. Т.е. процесс конечно можно смоделировать в пригодном для машины Тьюринга виде, но это будет тоже состояние. Машина Тьюринга не имеет памяти, т.е если остановить ее в какой-то момент, а потом запустить снова, она просто продолжит выполнять свой алгоритм с того места на котором остановилась. (Чего не делают, кстати сказать современные персональные компьютеры)
В результате мы имеем на выходе полную симметрию начальному условию:
Да, в задаче есть симметрия. Это видно из расположения допустимых состояний на ленте, они симметичны относительно середины. Если развернуть ленту в машине Тьюринга, но не изменять программу, то когда коза на одном берегу, а все остальные на другом, машина дойдет до решения за два перехода: крестьянин поедет за козой и перевезет ее на берег, где волк, в гордом одиночестве, пасет капусту.
… Осталось забрать козу.

Dr_Dash
15.10.2017 23:06По условиям оригинальной задачи, перемещение возможно только с участием крестьянина. А так получается у нас какая-то квантовая физика
вы здесь путаете физику и математику. Мы не обсуждаем детали перемещения козы, мы составляем математическую модель которая полностью описывает процесс, и эта «квантовая» коза просто напросто исключение математически незначащего случая — кто бы ни был с крестьянином, с ним всё будет в порядке, а вот «фейл» может произойти только в комбинациях на берегу. Так проще. Попробуйте применить свою модель не учитывая крестьянина и того кто с ним, и сами убедитесь что она станет проще.
lxsmkv Автор
16.10.2017 00:25от «мужика» избавиться не получается, это было бы недопустимым упрощением. Без него мы не сможем скомбинировать волка козу и капусту. Все таки мы перемещаем предметы из одной точки в другую и у нас есть паромщик. Если мы пренебрежём паромщиком, то у нас получится совсем другая задача. Важно при моделировании, не увлекаться и не уничтожить детали изначальной задачи, которая имеет вполне прикладной контекст. (Как в анекдоте про физика, инженера и математика на пожаре — «решение существует») При решении мы упрощаем до допустимой абстракции, а потом переводим решение, которое мы вывели для общего случая, обратно в предметную область.
Можно ведь вообще сказать «поменям берега местами» — задача решена. Нет так делать нельзя.
Dr_Dash
16.10.2017 01:16от «мужика» избавиться не получается, это было бы недопустимым упрощением.
вы заблуждаетесь. просто побудем математиками, представьте, что у нас может происходить телепортация предмета с берега на берег, или телепортационный обмен предметов на противоположных берегах — одно из двух, а паромщик в данном случае физически отсутствует с ними на берегу. Уберите из своей таблицы все строки/столбцы с P и получите этот случай и таблицу в два раза меньше
Dr_Dash
16.10.2017 01:23PS крайние случаи когда все трое вместе на берегу отбрасываем, потому что в этом случае либо паромщик сейчас возьмёт кого-то и повезёт(то есть останется только двое), либо они уже на другом берегу и паромщику плыть никуда не надо, т.е. как видите эти случаи исключаются из задачи, не влияя на дальнейший ход а в дальнейшем упоминание паромщика не требуется

lxsmkv Автор
16.10.2017 01:59я понимаю ход мысли, но делать так нельзя, иначе мы получим производную задачу. Полученное решение производной задачи нельзя будет перевести обратно в предметную область исходной задачи. swap (обмен) предметов противоречит механизму перемещения указанному в задаче, а он — челночный. И это важный аспект предметной области для которой мы ищем решение, и пренебрегать этим нельзя.
Но я не люблю словесных баталий, давайте лучше разберем эту производную задачу «на бумаге», чтобы было на что ссылаться. Обозначим козу 1, капусту 2, а волка 4. Не допустимой будет любая нечетная комбинация.
Изначально, по условию задачи, все находятся на одном берегу. Комбинация 7. Нечетная. Это недопустимое состояние. Давайте, ради продолжения мысленного эксперимента, выведем систему из недопустимого состояния, перенеся козу на другую сторону, как Вы предлагали в исходном комментарии.
Челнок находится на другом берегу. Там где коза. Возвращаем челнок к волку с капустой. Кого бы мы не переправили на другой берег (к козе) мы получим не допустимое состояние.
Эта производная задача не решается.
Продолжим мысленный эксперимент, пусть у нас будет портал, в который можно войти либо с одной стороны либо с другой. Перенеся один предмет через портал нельзя перенести следующий предмет в том же направлении, не перенеся какой-то предмет обратно. Т.е нельзя сделать два перемещения в одну сторону это бы противоречило условию задачи. (Мужик может и не нужен, но челнок никуда не деть, это важный аспект механики предметной области) Коза перебралась через портал.Теперь чтобы открыть портал со стороны волка с капустой снова, нужно перенести козу обратно. Эта производная задача не решается, потому, что пренебрегает устройством пропускного механизма. Он челночный.
Dr_Dash
16.10.2017 06:42Продолжим мысленный эксперимент, пусть у нас будет портал, в который можно войти либо с одной стороны либо с другой. Перенеся один предмет через портал нельзя перенести следующий предмет в том же направлении, не перенеся какой-то предмет обратно.
а случай когда мужик перевозит козу, потом возвращается обратно за капустой(не возвращая предмет обратно) не тот?
Челнок находится на другом берегу. Там где коза. Возвращаем челнок к волку с капустой. Кого бы мы не переправили на другой берег (к козе) мы получим не допустимое состояние.
Эта производная задача не решается.
Но мы можем привести к козе хоть волка хоть капусту а козу забрать обратно, (то что я описал как «телепортационный обмен предметов на противоположных берегах». )
Вы как-то не можете абстрагироваться от этого злополучного челнока. Я же написал вышепредставьте, что у нас может происходить телепортация предмета с берега на берег(крестьянин увёз козу), или телепортационный обмен предметов на противоположных берегах(привёз капусту, увёз козу обратно) — одно из двух,
это не какая-то «производная задача», это и есть та же самая задача, понимаете? И тогда у нас исчезает фигура крестьянина из таблицы, начисто. И при этом таблица полностью описывает задачу, здесь нет никакого обмана или искажения, это типа «тождественного преобразования».
lxsmkv Автор
16.10.2017 13:49да, теперь я понял, что не до конца понял. Под телепортацией я понял телепортацию с берега на берег. Но имеется ввиду, одновременная разгрузка-загрузка челнока. Тогда все как вы говорите. Спасибо за терпение. Распишу подробно для тех, кому интересно:
Коза садится в челнок и переправляется на другой берег, челнок возвращается, капуста загружается на челнок, челнок едет к козе, капуста выгружается на другой берег, а коза тут же загружается на челнок, коза едет к волку на берег, коза выгружается, а волк загружается и перезжает к капусте. Челнок возвращается пустой, забирает козу, и перевозит ее на другой берег.
Dr_Dash
17.10.2017 07:27Вы избавитесь от крестьянина, он по условию задачи лишний — там где он и так всё хорошо, а рассматривать нужно предельные случаи — когда он плывёт и не контролирует что там на берегах. Вы приведённую в своей публикации таблицу в 2 раза уменьшите.

Dr_Dash
15.10.2017 23:06попробуйте свой алгоритм для нескольких участников — мне было некогда я отложил на потом ) а так интересно поглядеть что будет

akhmelev
16.10.2017 07:36Динамическое программирование тут нужно, а не ооп и алгоритмизация рассуждениями.

vartv27
16.10.2017 10:41если будет 100+(коз, волков и крестьян), динамическое программирование на не чем не поможет, а рекурсию заменим на цикл и все будет прекрасно.
Scf
16.10.2017 12:192 волка, 2 козы, 2 капусты — задача уже неразрешима. Что бы крестьянин ни взял в лодку, будут жертвы.

Dr_Dash
16.10.2017 13:13а вот если добавить собаку-пастуха? Пока они с волком на берегу одни у них «вооружённый нейтралитет», а если оставить их с козой, то у волка взыграет кровожадность, а у собаки чувство долга и они сцепятся. вот кстати интересно

vaniacer
16.10.2017 15:29Убежден что работать должен компьютер. Пусть компьютер подставляет циферки не нужно перекладывать это на себя. Вот как я решил эту задачу на баше:
#!/bin/bash left_side=('goat' 'cabbage' 'wolf') right_side=() function check { case $1:$2 in 'goat':'cabbage' | 'cabbage':'goat' | 'wolf':'goat' | 'goat':'wolf' ) return 1;; *) return 0;; esac } while [[ ${left_side[@]} ]]; do for i in ${left_side[@]}; do passenger=${left_side[0]} unset left_side[0]; left_side=(${left_side[@]}) check ${left_side[@]} && { right_side+=("$passenger") echo -e "${left_side[@]}\n$passenger -->\n${right_side[@]}\n" } || { left_side+=("$passenger") continue } check ${right_side[@]} || { passenger=${right_side[0]} unset right_side[0]; right_side=(${right_side[@]}) left_side+=("$passenger") echo -e "${left_side[@]}\n<-- $passenger\n${right_side[@]}\n" continue } done done
Вывод:
cabbage wolf
goat -->
goat
wolf
cabbage -->
goat cabbage
wolf goat
< — goat
cabbage
goat
wolf -->
cabbage wolf
goat -->
cabbage wolf goat
vaniacer
16.10.2017 15:52А потом делается рефакторинг:)
#!/bin/bash left_side=(${1:-'goat'} ${2:-'cabbage'} ${3:-'wolf'}) right_side=() function check { case $1:$2 in 'goat':'cabbage' | 'cabbage':'goat' | 'wolf':'goat' | 'goat':'wolf' ) return 1;; *) return 0;; esac } while [[ ${left_side[@]} ]]; do passenger=${left_side[0]}; unset left_side[0]; left_side=(${left_side[@]}) check ${left_side[@]} && { right_side+=("$passenger") echo -e "${left_side[@]}\n$passenger -->\n${right_side[@]}\n"; } || { left_side+=("$passenger"); } check ${right_side[@]} || { passenger=${right_side[0]} unset right_side[0] right_side=(${right_side[@]}) left_side+=("$passenger") echo -e "${left_side[@]}\n<-- $passenger\n${right_side[@]}\n" } done


LightSUN
Имхо сложность тут вовсе не алгоритмическая, а в том, что под «перевезти» в жизни понимается перемещение груза только в одно направление — вся «сложность» в том, чтобы догадаться, что можно груз возить обратно.
lxsmkv Автор
Очень верное замечание. В задаче имеется неявное правило. Именно поэтому я думаю, в программировании всегда нужен будет человек, чтобы из задачи сформулированной на человеческом языке, выделять правила явные, и неявные. Это как раз то, что мы понимаем под словом «думать» и чему, как мне кажется, машина в сегодняшнем ее виде, никогда не сможет «научиться».
lxsmkv Автор
Я тут еще размышлял над этим, и мне стало ясно, что выведение правил и условий из поставленной задачи по сути явлется анализом требований. Значит requirements engineering это интересная и чертовски сложная умственная работа. И, ссылаясь на замечание Dr_Dash ниже, любопытно, что хороший инженер выведет условия как в статье, а превосходный инженер скажет, что «мужик не нужен». И сэкономит этим самым деньги клиента.