Если ты на практике используешь ООП, то хорошо разбираешься в таких вещах, как «паттерны проектирования». А знаешь ли ты, что есть множество полезных паттернов, которые не укладываются в этот стандартный список? К сожалению, многие из них связаны с «функциональным программированием», которое, согласно легенде, сложное и заумное. Если десять раз сказать слово «моноид», можно вызвать Дьявола.

Mark Seeman расскажет о функциональном программировании просто и быстро. Для этого он начал писать цикл статей, посвященных связи между паттернами проектирования и теорией категорий. Любой ООПшник, у которого есть 15 минут свободного времени, сможет заполучить в свои руки принципиально новый набор идей и инсайтов, касающихся не только функциональщины, но и правильного объектно-ориентированного дизайна. Решающим фактором является то, что все примеры — это реальный код на C#, F# и Haskell. Этот хабрапост — перевод самого начала цикла, первых трех статей, слитых воедино для удобства понимания.

Кроме того, с Марком можно пообщаться вживую, посетив конференцию DotNext 2017 Moscow, которая состоится 12-13 ноября 2017 г. в Москве, в «Славянская Рэдиссон». Марк прочитает доклад на тему «From dependency injection to dependency rejection». Билеты можно взять здесь.

Вступление. Моноиды, полугруппы и все-все-все

Этот текст является частью новой серии о связях между паттернами проектирования и теорией категорий.
Функциональное программирование обычно критикуют за особый заумный жаргон. Термины типа зигохистоморфный препроморфизм никак не помогают донести суть новичкам. Но прежде чем бросаться камнями, вначале мы должны выйти из собственного стеклянного домика. В объектно-ориентированном проектировании используются названия типа Bridge, Visitor, SOLID, связность и другие. Слова звучат знакомо, но можете ли вы объяснить или реализовать в коде паттерн Visitor или описать, что такое «связность»?

Слово «bridge» само по себе не делает объектно-ориентированную терминологию лучше. Возможно, оно даже делает ее хуже. В конце концов, слово стало многозначным: имеем ли мы в виду настоящий физический объект, объединяющий два разных места, или разговариваем о паттерне проектирования? Конечно, на практике, мы поймем это из контекста, но это не отменяет факта — если кто-то говорит о паттерне bridge, вы совершенно ничего не поймете, если заранее не выучили его. То, что слово звучит знакомо, еще не делает его полезным.

Многие объектно-ориентированные программисты открыли для себя полезность «операции, которая возвращает тот же тип, какой она получила в качестве аргумента». Но тем не менее, такое описание, такой словарь — очень неудобны. Не лучше ли описать эту операцию одним словом? Может быть, это моноид или полугруппа?

Объектно-ориентированные озарения

В книге Domain-Driven Design Эрик Эванс рассказывает о понятии Closure of Operations. Как и следует из названия, это «операция, у возвращаемый тип которой совпадает с типами аргументов». В C# это может быть метод с сигнатурой public Foo Bar(Foo f1, Foo f2). Метод берет на вход два объекта Foo и возвращает тоже объект Foo.

Как заметил Эванс, спроектированные таким образом объекты начинают выглядеть, как если бы они формировали арифметику. Если есть операция, принимающая Foo и возвращающая Foo, что это может быть? Может быть, сложение? Умножение? Еще какая-то математическая операция?

Кое-какие enterprise разработчики просто хотят «сделать дело и двигаться дальше», их совершенно не беспокоит математика. Для них идея делать код более «математичным» кажется очень спорной. Тем не менее, даже если вам «не нравится математика», вы точно понимаете смысл сложения, умножения и т.п. Арифметика — мощная метафора, поскольку все программисты ее понимают.

В своей знаменитой книге «Test-Driven Development: By Example» Кент Бек, похоже, эксплуатировал ту же самую идею. Хотя не думаю, что он где-то напрямую об этом написал.

То, о чем писал Эванс — это моноиды, полугруппы и похожие на них концепции из абстрактной алгебры. Справедливости ради, я недавно с ним общался, и сейчас он уже отлично разбирается во всех этих вещах. Разбирался ли он в них в 2003 году, когда была написана DDD — не знаю, но я — точно нет. Моя задача здесь не тыкать пальцами, а показать, что очень умные люди вывели принципы, которые можно использовать в ООП, задолго до того, как эти принципы получили собственные имена.

Как все это связано

Моноиды и полугруппы относятся к большей группе операций, называющейся магмами. Об этом мы поговорим позже, а сейчас начнем с моноидов, продолжим полугруппами и только потом перейдем к магмам. Все моноиды являются полугруппами, обратное не верно. Другими словами, моноиды формируют подмножество полугрупп.

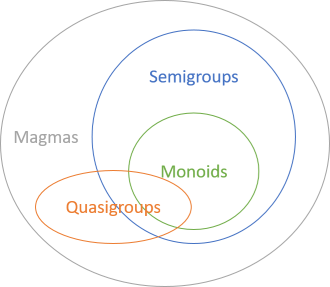
Они описывают бинарные операции в форме: операция, которая берет на вход два значения Foo и возвращает значение типа Foo на выходе. Обе категории описываются (интуитивно-понятными) законами. Разница в том, что законы моноидов строже, чем законы полугрупп. Не зависайте на терминологии: слово «закон» может звучать, как будто здесь замешана серьезная сложная математика, но эти «законы» — простые и интуитивные. О них мы поговорим в следующих частях (которых будет около 15 штук).

Несмотря на то, что все они тесно связаны с математикой, они предназначены для того, чтобы, в том числе, дать множество идей для хорошего объектно-ориентированного проектирования.

Резюме

Для обычного объектно-ориентированного программиста термины типа моноид или полугруппа за версту пахнут математикой, академией и башнями из слоновой кости, заселенными архитектурными астронавтами. Но на самом деле, это простые и удобные идеи, которые может понять каждый, кому не лень потратить на это 15 минут.

Часть 1. Моноиды

Суть: введение в моноиды для ООП-программистов.
Данный раздел является частью цикла статей о моноидах, полугруппах и связанных с ними концепциях. Изучив этот раздел, вы поймете, что такое моноид и чем он отличается от полугруппы.

Моноиды образуют подмножество полугрупп. Правила, по которым работают моноиды, строже, чем для полугрупп. Можно даже решить, что лучше вначале разобраться с полугруппами и уже на их основе продвигаться к моноидам. Строго говоря, с точки зрения иерархии, это имеет смысл. Но я думаю, что моноиды куда более интуитивны. Увидев первый же пример моноида, сразу понимаешь, что они описывают вещи из повседневной жизни. Легко найти пример для моноида, а вот чтобы подобрать хороший пример полугруппы — придется постараться. Поэтому мы начнем именно с моноидов.

Законы моноида

Что общего имеет сложение (40 + 2) и умножение (6 * 7)?
Обе эти операции

• ассоциативны
• являются бинарными операциями
• имеют нейтральный элемент

Это все, что нужно для образования моноида. Ассоциативность и существование нейтрального элемента называют «законами моноида» или «моноидными законами» (в английском языке — monoid laws). Стоит отметить, что моноид — это комбинация типа данных и операции. То есть, это не просто тип, а скорее функция (или метод), которая работает над этим типом. Например, сложение и умножение — это два разных моноида, работающих на числах.

Бинарность

Давайте начнем с самого простого. Операция является «бинарной», если она работает над двумя значениями. Возможно, при упоминании слова «бинарный» вам в первую очередь представляются бинарные данные, типа 101010, но это слово взялось из латинского языка, и означает что-то связанное с «арностью два». Астрономы тоже иногда говорят о двойных звездах (binary stars), но сейчас это слово в основном используется в контексте компьютеров: кроме бинарных данных, вы, скорее всего, слышали и о бинарных деревьях. Говоря о бинарных операциях, мы подразумеваем, что оба входящих значения имеют один и тот же тип, и что возвращаемый тип также совпадает со входящим типом. Другими словами, в C# метод типа этого является корректной бинарной операцией:

public static Foo Op(Foo x, Foo y)

Иногда, если Op является методом экземпляра класса Foo, она может выглядеть вот так:

public Foo Op (Foo foo)

С другой стороны, вот это уже не является бинарной операцией:

public static Baz Op(Foo f, Bar b)

Несмотря на то, что оно принимает два входящих аргумента, они имеют разные типы, и возвращаемый тип тоже отличается.

Поскольку все аргументы и возвращаемые значения совпадают по типу, бинарная операция представляет собой то, что Эрик Эванс в Domain-Driven Design называл Closure of Operations.

Ассоциативность

Для образования моноида бинарная операция обязательно должна быть ассоциативной. Это означает попросту то, что порядок вычислений не важен. Например, для сложения это значит, что:

(2 + 3) + 4 = 2 + (3 + 4) = 2 + 3 + 4 = 9

Аналогично для умножения:

(2 * 3) * 4 = 2 * (3 * 4) = 2 * 3 * 4 = 24

Если говорить об описанном выше методе Op, ассоциативность требует, чтобы areEqual оказался равен true для следующего кода:

var areEqual = foo1.Op(foo2).Op(foo3) == foo1.Op(foo2.Op(foo3));

На левой части вначале вычислится foo1.Op(foo2), и затем результат применится к foo3. Справа первым вычислится foo2.Op(foo3), и результат станет аргументом для foo1.Op. Поскольку левая и правая части сравниваются с помощью оператора ==, ассоциативность требует, чтобы areEqual оказался равен true.

Чтобы вся эта конструкция заработала в C#, если имеется какой-то самодельный моноид Foo, у него придется перегрузить Equals и реализовать оператор ==.

Нейтральный элемент

Третье правило моноида заключается в том, что должен существовать нейтральный элемент. Обычно его называют единицей (не самое подходящее имя, но лучше, чем громоздкое «нейтральный элемент»). В дальнейшем будем называть его так.

Единица — это значение, которое «ничего не делает». Например, для сложения — это 0, поскольку добавление нуля ничего не делает с исходным значением, не изменяет его:

0 + 42 = 42 + 0 = 42

Простое упражнение: догадайтесь, чем является единица для умножения.

В приведенной выше записи суммы подразумевается, что единица должна нейтрально работать и когда ее применяют слева, и когда ее применяют справа. Для наших объектов Foo это можно записать так:

var hasIdentity =
    Foo.Identity.Op(foo) == foo.Op(Foo.Identity) &&
    foo.Op(Foo.Identity) == foo;

Существует пара моноидов, работающих над булевскими значениями: all и any. Как думаете, как они работают? Какие у них единицы?

Поразмышлять над all и any (или нагуглить их) вы можете в качестве упражнения. В следующих разделах я покажу другие, более интересные моноиды. В этом хабрапосте рассматриваются только строки, списки и последовательности — остальные статьи все еще пишутся.

В сущности, если есть тип данных, который «ведет себя как число», скорей всего можно сделать из него моноид. Сложение — один из лучших кандидатов, ведь его проще всего понять, и не нужно связываться с вещами типа единиц измерения. Например, в .NET Base Class Library существует структура TimeSpan, имеющая метод Add. Оператор == у нее тоже имеется. С другой стороны, у TimeSpan нет метода Multiply, поскольку — что будет результатом умножения двух периодов? Квадратное время?

Резюме

Моноид (не путать с монадой) — это бинарная операция, которая удовлетворяет двум законам моноида: операция должна быть ассоциативной и должен существовать нейтральный элемент (единица). Основными примерами моноида являются сложение и умножение, но существуют и многие другие.

(Кстати, единица для умножения — это единица (1), all — это булевский and, а any — булевский or.)

Часть 2. Моноид строк, списков и последовательностей

Суть: строки, списки и последовательности, по сути, являются одним и тем же моноидом.
Данный раздел является частью цикла статей о моноидах.
Вкратце, моноид — это ассоциативная бинарная операция с нейтральным элементом (известным как единица, или в английской терминологии —identity).

Последовательности

В C# ленивые последовательности значений моделируются с помощью IEnumerable<T>. Можно комбинировать пару последовательностей, добавляя одну к другой:

xs.Concat(ys)

Здесь xs и ys — экземпляры IEnumerable<T>. Метод расширения Concat объединяет последовательности. Он имеет следующую сигнатуру: IEnumerable<T> Concat<T>(IEnumerable<T>, IEnumerable<T>), поэтому является бинарной операцией. Если мы выясним, что он ассоциативен и имеет единицу, то докажем, что это — моноид.

Последовательности ассоциативны, потому что последовательность вычисления не изменяет результата. Ассоциативность — свойство моноида, поэтому один из способов продемонстрировать его — использовать property-based testing.

[Property(QuietOnSuccess = true)]
public void ConcatIsAssociative(int[] xs, int[] ys, int[] zs)
{
    Assert.Equal(
        xs.Concat(ys).Concat(zs),
        xs.Concat(ys.Concat(zs)));
}

Этот автотест использует FsCheck (да, в C# он тоже работает!) для демонстрации ассоциативности Concat. Чтобы упростить дело, xs, ys и zs объявяются как массивы. Это нужно потому, что FsCheck нативно знает, как создавать массивы, а вот встроенной поддержки IEnumerable<T> не имеет. Конечно, можно было бы посоздавать iEnumerable<T> самостоятельно, с помощью FsCheck API, но это усложнит пример, а ничего нового не добавит. Свойство ассоциативности выполняется и для других чистых реализаций IEnumerable<T>. Если не верите — попробуйте.

Операция Concat имеет единицу. Единица — это пустая последовательность, что подтверждается следующим тестом:

[Property(QuietOnSuccess = true)]
public void ConcatHasIdentity(int[] xs)
{
    Assert.Equal(
        Enumerable.Empty<int>().Concat(xs),
        xs.Concat(Enumerable.Empty<int>()));
    Assert.Equal(
        xs,
        xs.Concat(Enumerable.Empty<int>()));
}

Иначе говоря, если в начало или конец любой последовательности приклеить пустую последовательность, то изначальная последовательность не изменится.

Поскольку Concat — ассоциативная бинарная операция с единицей, она является моноидом. Доказано. ?

Связные списки и другие коллекции

Приведенные выше тесты с использованием FsCheck показали, что Concat — это моноид над массивами. Это свойство сохраняется для всех чистых реализаций IEnumerable<T>.

В Haskell ленивые последовательности моделируется в виде связных списков. Они ленивы уже потому, что все выражения в Haskell являются таковыми по умолчанию. Законы моноидов выполняются и для списков в Haskell:

?> ([1,2,3] ++ [4,5,6]) ++ [7,8,9]
[1,2,3,4,5,6,7,8,9]
?> [1,2,3] ++ ([4,5,6] ++ [7,8,9])
[1,2,3,4,5,6,7,8,9]

?> [] ++ [1,2,3]
[1,2,3]
?> [1,2,3] ++ []
[1,2,3]

В Haskell оператор ++ — примерно то же, что Concat в C#, но эту операцию принято называть сложением или присоединением (append), а не конкатенацией (concat).

В F# связные списки инициализируются агрессивно (не лениво), поскольку все выражения в F# являются таковыми по умолчанию. Списки, тем не менее, продолжают быть моноидами, поскольку все свойства моноида все еще выполняются:

> ([1; 2; 3] @ [4; 5; 6]) @ [7; 8; 9];;
val it : int list = [1; 2; 3; 4; 5; 6; 7; 8; 9]
> [1; 2; 3] @ ([4; 5; 6] @ [7; 8; 9]);;
val it : int list = [1; 2; 3; 4; 5; 6; 7; 8; 9]

> [] @ [1; 2; 3];;
val it : int list = [1; 2; 3]
> [1; 2; 3] @ [];;
val it : int list = [1; 2; 3]

В F# оператором конкатенации является @, а не ++, но его поведение точно такое же, как в Haskell. ?

Строки

Никогда не задумывались, почему текстовые значения называются string в большинстве языков программирования? В конце концов, string в английском языке — это веревка, такая длинная гибкая штука, сделанная из волокон.

В программировании текст обычно представляется в памяти как последовательный блок символов. Обычно программа читает такие последовательные блоки памяти до тех пор, пока не достигает чего-то, являющегося признаком конца строки. Таким образом, строки символов упорядочены. Они похожи на последовательности или списки.

На самом деле, в Haskell тип String — это не что-то хитрое, а синоним для [Char] (это значит: список значений Char). Поэтому все, что вы можете делать со списками любых других типов, можно делать и со String:

?> "foo" ++ []
"foo"
?> [] ++ "foo"
"foo"
?> ("foo" ++ "bar") ++ "baz"
"foobarbaz"
?> "foo" ++ ("bar" ++ "baz")
"foobarbaz"

Совершенно очевидно, что ++ для String является моноидом в Haskell.

Точно так же, в .NET, System.String реализует IEnumerable<char>. По аналогии можно догадаться, что они окажутся моноидами — и это почти так. Давайте посмотрим, они точно ассоциативны:

[Property(QuietOnSuccess = true)]
public void PlusIsAssociative(string x, string y, string z)
{
    Assert.Equal(
        (x + y) + z,
        x + (y + z));
}

В C# оператор + действительно определен для string, и, как видно по этому тесту на FsCheck, он ассоциативен. И он почти имеет единицу. Что является эквивалентом пустому списку в мире строк? Конечно, пустая строка:

[Property(QuietOnSuccess = true)]
public void PlusHasIdentity(NonNull<string> x)
{
    Assert.Equal("" + x.Get, x.Get + "");
    Assert.Equal(x.Get, x.Get + "");
}

Пришлось вручную объяснить FsCheck, что использовать null не нужно. Как всегда, null вставляет палки в колеса в любые рассуждения о коде.

Проблема здесь в том, что "" + null и null + "" возвращают одно и то же значение — "", и оно не равно входящему значению (null). Другими словами, "" не является настоящей единицей для оператора +, потому что существует вот этот специальный случай. (И кстати, null также не является единицей, поскольку null + null возвращает… ""! Ну конечно, он возвращает именно это…). Тем не менее, это особенность реализации. В качестве упражнения, попробуйте придумать метод (расширения) на C#, который сделал бы string правильным моноидом, несмотря на наличие null. Как только вы его придумаете, это сразу покажет, что конкатенация строк является моноидом в .NET точно так же, как и в Haskell. ?

Свободный моноид

Вспомните, как в предыдущих статьях мы показали, что и сложение, и умножение чисел являются моноидами. Существует еще как минимум один моноид над числами, и это — последовательность. Если существует обобщенная последовательность (IEnumerable<T>), она может содержать все, что угодно, включая числа.

Представьте, что есть два числа, 3 и 4, и хочется объединить их, но еще пока непонятно — каким именно образом вы будете их объединять. Чтобы отложить решение, можно положить оба числа в единичный массив (в английском языке это называется singleton array — массив с одним элементом, и это не имеет ничего общего с паттерном Singleton):

var three = new[] { 3 };
var four = new[] { 4 };

Как мы раньше доказали, последовательности являются моноидами, поэтому можно спокойно комбинировать их:

var combination = three.Concat(four);

В результате получается последовательность, содержащая оба числа. В данный момент, мы еще не потеряли никакой информации, поэтому как только будет понятен способ комбинирования этих чисел, нужно будет просто вычислить собранные ранее данные. Это называется свободным моноидом.

Например, мы решили, что нужно получить сумму чисел:

var sum = combination.Aggregate(0, (x, y) => x + y);

(Да, я в курсе, что существует метод Sum, но сейчас наша цель — разобраться в деталях). Этот Aggregate принимает первым аргументом значение seed, а вторым — функцию для комбинирования.

А вот так можно получить произведение:

var product = combination.Aggregate(1, (x, y) => x * y);

Заметьте, что в обоих случаях значение seed является единицей для соответствующей моноидальной операции: 0 — для сложения, 1 — для умножения. Точно так же, функция аггрегации использует ту бинарную операцию, которая относится к соответствующему моноиду.

Интересно, что это называется «свободным моноидом», аналогично «свободным монадам». В обоих случаях можно собрать все данные, интерпретируя их не сразу, а позже — и потом сгрузить все эти данные в один из многих заранее заготовленных «вычислителей».

Резюме

Многие типы коллекций, такие как последовательности и массивы в .NET или списки в F# и Haskell, являются моноидами над конкатенацией. В Haskell строки являются списками, поэтому строковая конкатенация автоматически является моноидом. В .NET оператор + для строк является моноидом, но только если притвориться, что null не существует. Тем не менее, все они являются вариациями одного и того же моноида.

Хорошо, что C# использует + для конкатенации строк, поскольку, как было показано в предыдущей части, сложение — наиболее интуитивное и «естественное» из всех моноидов. Вы знаете школьную арифметику, поэтому можете мгновенно понять метафору сложения. Тем не менее, моноид — это больше, чем метафора. Это абстракция, которая описывает специальные бинарные операции, одна из которых (так получилось) является сложением. Это генерализация концепции — и это абстракция, которую вы уже знаете.

Заключение

На этом мы завершаем эту статью. Впереди еще очень много информации, которая будет публиковаться так же, как в оригинале — в виде последовательных постов на Хабре, связанных обратными ссылками. Здесь и далее: оригиналы статей — © Mark Seemann 2016, переводы делаются силами JUG.ru Group, переводчик — Олег Чирухин.

Напоминаем, что пообщаться с автором можно вживую, посетив конференцию DotNext 2017 Moscow, которая состоится 12-13 ноября 2017 г. в Москве, в «Славянская Рэдиссон». Марк прочитает доклад на тему «From dependency injection to dependency rejection». Билеты можно взять здесь.