Из-за всеобщего бума блокчейна и всякой бигдаты с первых строчек техноновостей сошла другая перспективная тема — квантовые вычисления. А они, между прочим, способны перевернуть сразу несколько ИТ-областей, начиная с пресловутого блокчейна и заканчивая инфобезопасностью. В двух ближайших статьях Сбербанк и Сбербанк-Технологии расскажут, чем круты квантовые вычисления и что вообще с ними делают сейчас.

Чтобы разобраться с квантовыми вычислениями, стоит для начала освежить знания о классических. Здесь единицей обрабатываемой информации является бит. Каждый бит может находиться только в одном из двух возможных состояний – 0 или 1. Регистр из N бит может содержать одну из 2N возможных комбинаций состояний и представляется в виде их последовательности.
Для обработки и преобразования информации используются побитовые операции, пришедшие из булевой алгебры. Основные операции — это однобитная NOT и двубитные AND и OR. Битовые операции описываются через таблицы истинности. В них приводится соответствие входных аргументов получаемому значению.
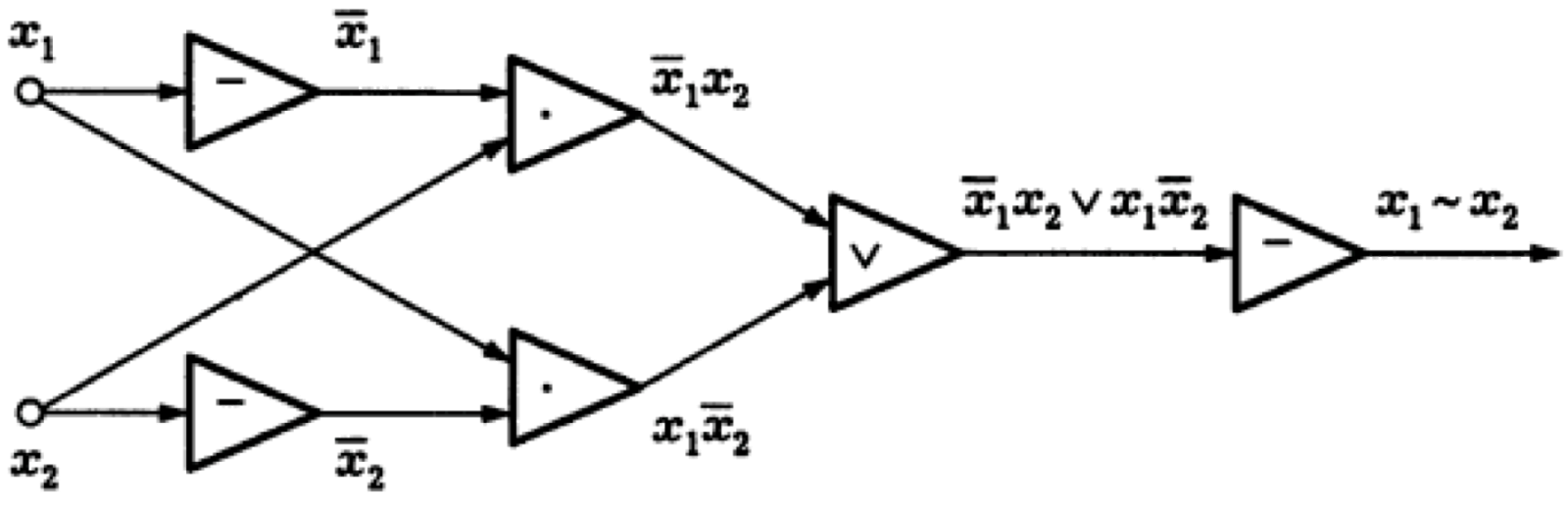
Алгоритм классических вычислений — это набор последовательных битовых операций. Удобней всего воспроизводить его графически, в виде схемы из функциональных элементов (СФЭ), где каждая операция имеет свое обозначение. Вот пример СФЭ для проверки двух бит на эквивалентность.
А теперь перейдем к новой теме. Квантовые вычисления — это альтернатива классическим алгоритмам, основанная на процессах квантовой физики. Она гласит, что без взаимодействия с другими частицами (то есть до момента измерения), электрон не имеет однозначных координат на орбите атома, а одновременно находится во всех точках орбиты. Область, в которой находится электрон, называется электронным облаком. В ходе известного эксперимента с двумя щелями один электрон проходит одновременно через обе щели, интерферируя при этом с самим собой. Только при измерении эта неопределенность схлопывается и координаты электрона становятся однозначными.

Вероятностный характер измерений, присущий квантовым вычислениям, лежит в основе многих алгоритмов – например, поиск в неструктурированной БД. Алгоритмы данного типа пошагово увеличивают амплитуду правильного результата, позволяя получить его на выходе с максимальной вероятностью.
В квантовых вычислениях физические свойства квантовых объектов реализованы в так называемых кубитах (q-bit). Классический бит может находиться только в одном состоянии – 0 или 1. Кубит до измерения может находиться одновременно в обоих состояниях, поэтому его принято обозначать выражением a|0? + b|1?, где A и B — комплексные числа, удовлетворяющие условию |A|2+|B|2=1. Измерение кубита мгновенно «схлопывает» его состояние в одно из базисных – 0 или 1. При этом «облако» коллапсирует в точку, первоначальное состояние разрушается, и вся информация о нем безвозвратно теряется.

Одно из применений этого свойства –кот Шредингера генератор истинно случайных чисел. Кубит вводится в такое состояние, при котором результатом измерения могут быть 1 или 0 с одинаковой вероятностью. Это состояние описывается так:
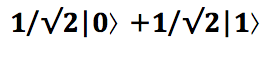
Начнем с основ. Имеется набор исходных данных для вычислений, представленный в двоичном формате векторами длиной N.
В классических вычислениях в память компьютера загружается только один из 2n вариантов данных и для этого варианта вычисляется значение функции. В результате одновременно обрабатывается только один из 2n возможных наборов данных.
В памяти квантового компьютера одновременно представлены все 2n комбинации исходных данных. Преобразования применяются ко всем этим комбинациям сразу. В результате за одну операцию мы вычисляем функцию для всех 2n возможных вариантов набора данных (измерение в итоге все равно даст только одно решение, но об этом позже).
И в классических, и в квантовых вычислениях используются логические преобразования — гейты. В классических вычислениях входные и выходные значения хранятся в разных битах, а значит в гейтах количество входов может отличаться от количества выходов:

Рассмотрим реальную задачу. Нужно определить, эквивалентны ли два бита.
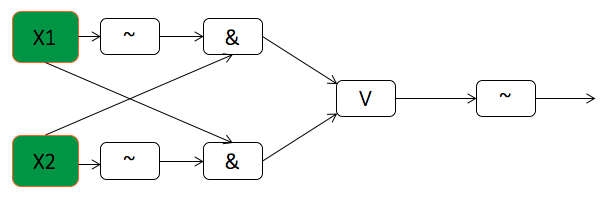
Если при классических вычислениях на выходе получаем единицу, значит эквивалентны, иначе нет:
Теперь представим эту задачу с помощью квантовых вычислений. В них все гейты преобразований имеют столько же выходов, сколько входов. Это связано с тем, что результатом преобразования является не новое значение, а изменение состояния текущих.
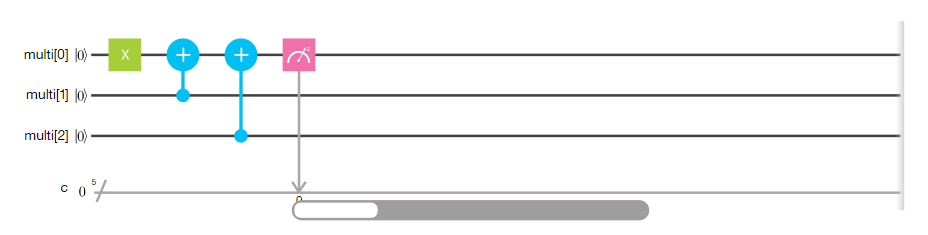
В примере мы сравниваем значения первого и второго кубитов. Результат будет в нулевом кубите — кубите-флаге. Данный алгоритм применим только к базовым состояниям – 0 или 1. Вот порядок квантовых преобразований.
Попробуем сравнить классические и квантовые вычисления в более серьезных задачах. Для этого нам потребуется еще немного теоретических знаний.
В квантовых вычислениях обрабатываемая информация закодирована в квантовых битах – так называемых кубитах. В простейшем случае кубит, как и классический бит, может находиться в одном из двух базисных состояний: |0? (краткое обозначение для вектора 1|0? + 0|1?) и |1? (для вектора 0|0? + 1|1?). Квантовый регистр представляет собой тензорное произведение векторов кубит. В простейшем случае, когда каждый кубит находится в одном из базисных состояний, квантовый регистр эквивалентен классическому. Регистр из двух кубит, находящихся в состоянии |0>, можно расписать в таком виде:
(1|0? + 0|1?)*(1|0? + 0|1?) = 1|00? + 0|01? + 0|10? + 0|11? = |00?.
Для обработки и преобразования информации в квантовых алгоритмах используются так называемые квантовые вентили (гейты). Они представляются в виде матрицы. Для получения результата применения гейта, нам необходимо умножить вектор, характеризующий кубит, на матрицу гейта. Первая координата вектора – множитель перед |0?, вторая координата – множитель перед |1?. Матрицы основных однокубитных гейтов выглядит так:

А вот пример применения гейта Not:
X * |0? = X * (1|0? + 0|1?) = 0|0? + 1|1? = |1?
Множители перед базисными состояниями называются амплитудами и являются комплексными числами. Модуль комплексного числа равен корню из суммы квадратов действительной и мнимой частей. Квадрат модуля амплитуды, стоящей перед базисным состоянием, равен вероятности получить это базисное состояние при измерении кубита, поэтому сумма квадратов модулей амплитуд всегда равна 1. Мы могли бы использовать произвольные матрицы для преобразований над кубитами, но из-за того, что норма (длина) вектора всегда должна быть равна 1 (сумма вероятностей всех исходов всегда равна 1), наше преобразование должно сохранять норму вектора. Значит преобразование должно быть унитарным и соответствующая ему матрица унитарной. Напомним, что унитарное преобразование обратимо и UU†=I.
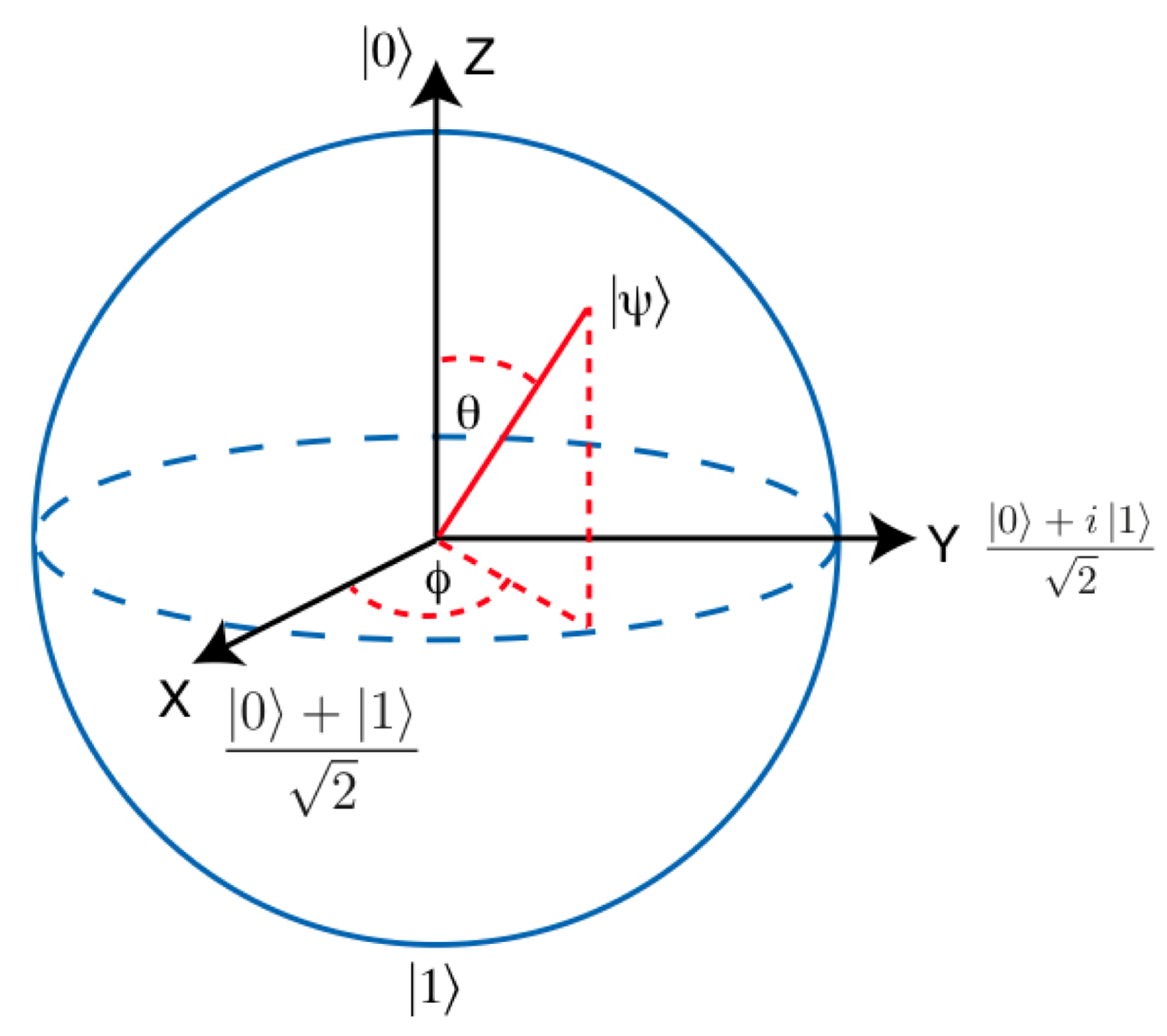
Для более наглядной работы с кубитами их изображают векторами на сфере Блоха. В такой интерпретации однокубитные гейты представляют собой вращение вектора кубита вокруг одной из осей. Например гейт Not (X) поворачивает вектор кубита на Pi относительно оси X. Таким образом, состояние |0>, представляемое вектором, направленным строго вверх, переходит в состояние |1>, направленное строго вниз. Состояние кубита на сфере Блоха определяется формулой cos(?/2)|0?+ei?sin(?/2)|1?
Для построения алгоритмов нам недостаточно только однокубитных гейтов. Необходимы гейты, которые осуществляют преобразования в зависимости от некоторых условий. Основным таким инструментом является двухкубитный гейт CNOT. Этот гейт применяется к двум кубитам и инвертирует второй кубит только в том случае, если первый кубит находится в состоянии |1?. Матрица гейта CNOT выглядит так:
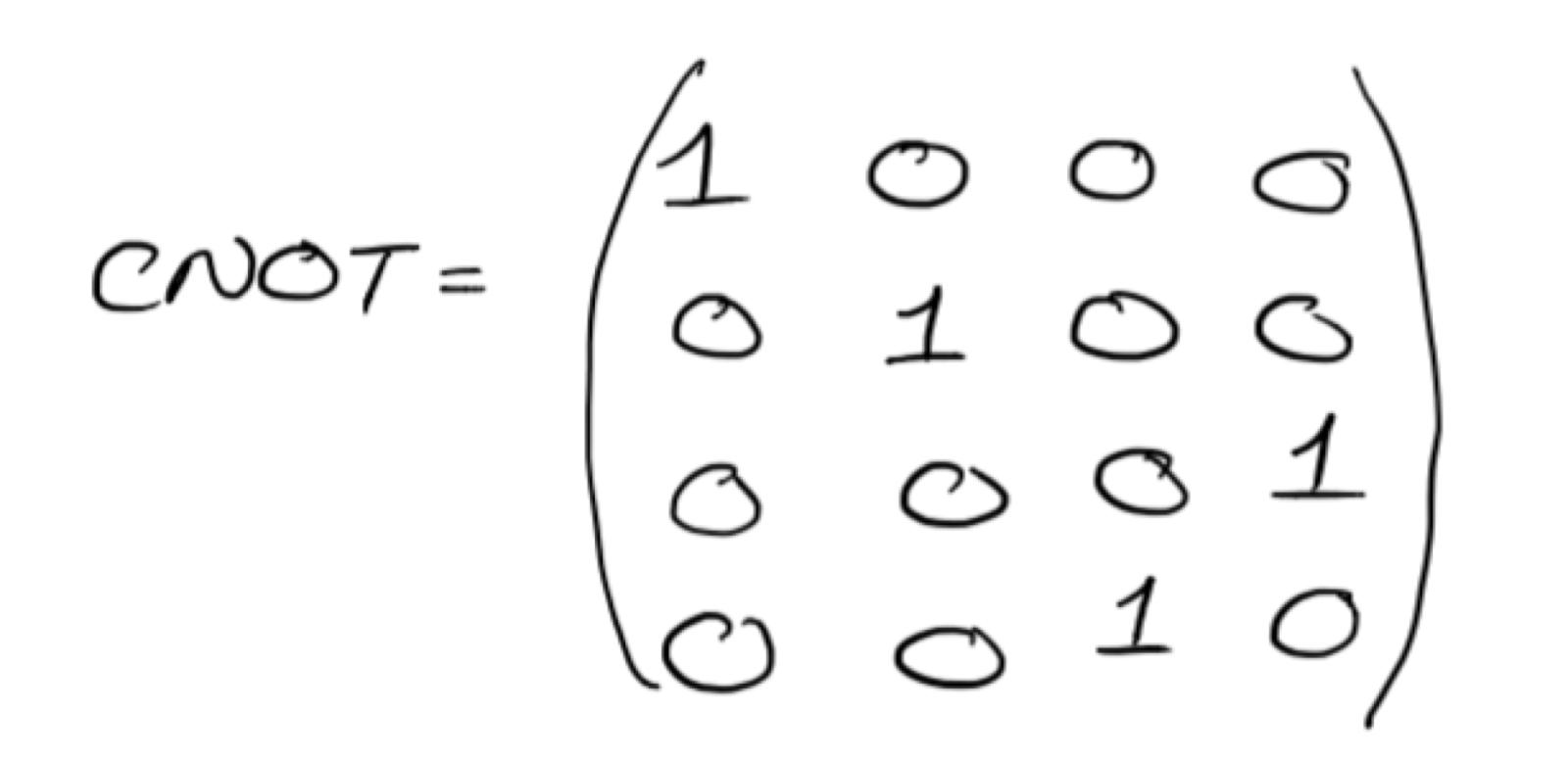
А вот пример применения:
CNOT *|10? = CNOT * (0|00? + 0|01? + 1|10? + 0|11?) = 0|00? + 0|01? + 1|11? + 0|10? = |11?
Применение гейта CNOT эквивалентно выполнению классической операции XOR с записью результата во второй кубит. Действительно, если посмотреть на таблицу истинности оператора XOR и CNOT, то увидим соответствие:
У гейта CNOT есть интересное свойство – после его применения кубиты запутываются или распутываются, в зависимости от исходного состояния. Это будет показано в следующей статье, в разделе про квантовый параллелизм.
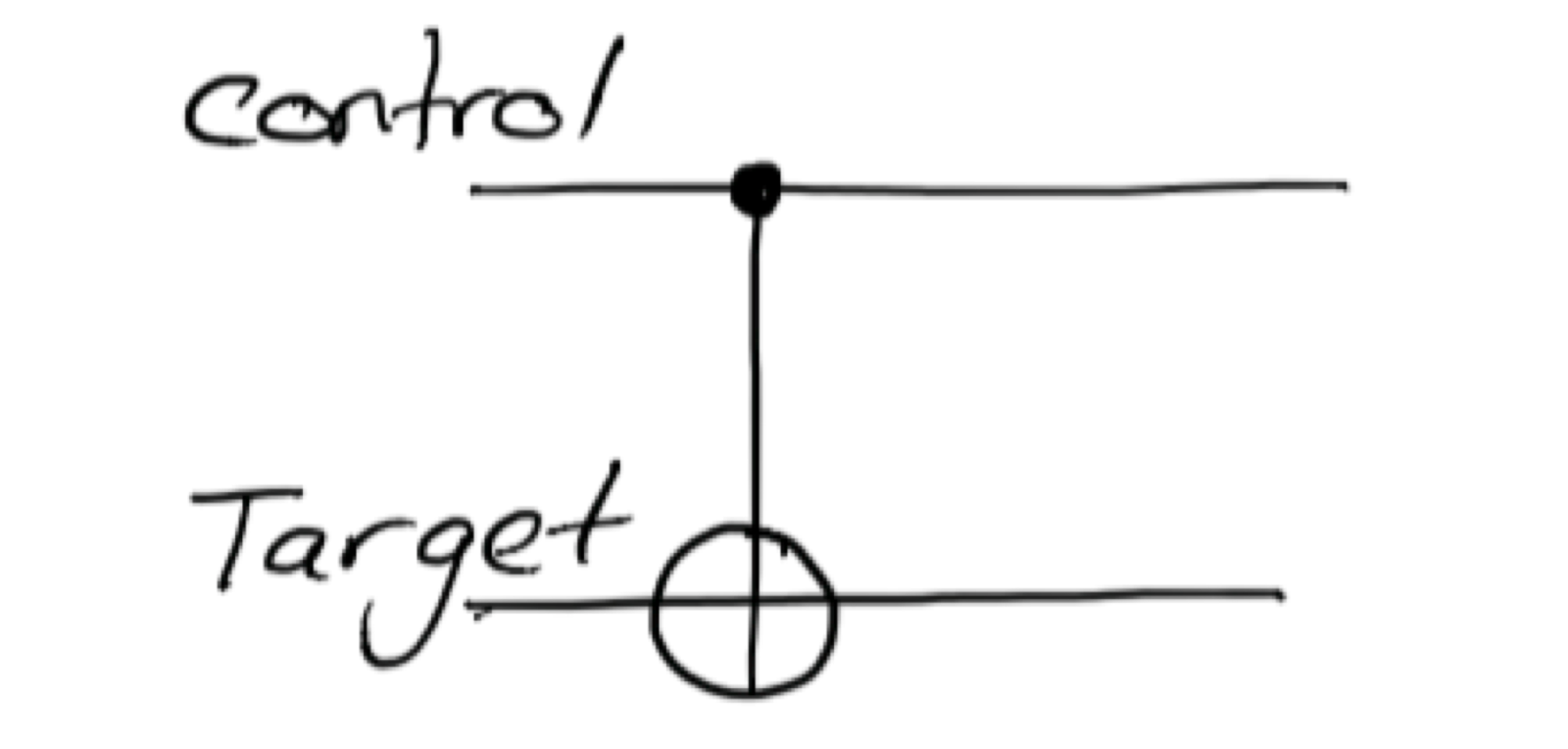
Имея полный арсенал квантовых гейтов, мы можем приступать к разработке квантовых алгоритмов. В графическом представлении кубиты представляются прямыми линиями – «струнами», на которые накладываются гейты. Однокубитные гейты Паули обозначаются обычными квадратами, внутри которых изображается ось вращения. Гейт CNOT выглядит немного сложнее:
Пример применения гейта CNOT:
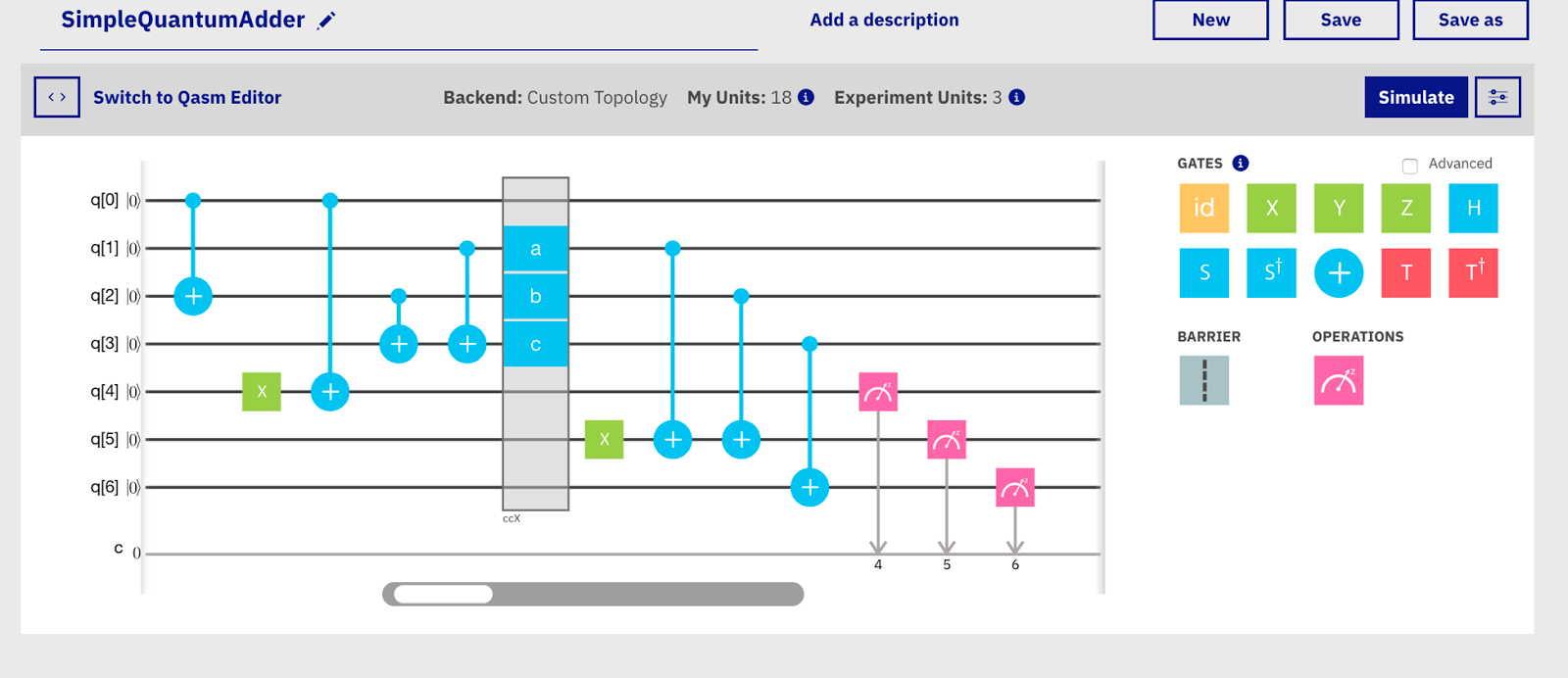
Одним из важнейших действий в алгоритме является измерение полученного результата. Измерение обычно обозначается дуговой шкалой со стрелкой и обозначением, относительно какой оси идет измерение.
Итак, попробуем построить классический и квантовый алгоритм, который прибавляет 3 к аргументу.
Суммирование обычных чисел столбиком подразумевает совершение двух действий над каждым разрядом – сумму самих цифр разряда и сумму результата с переносом с предыдущей операции, если таковой перенос был.
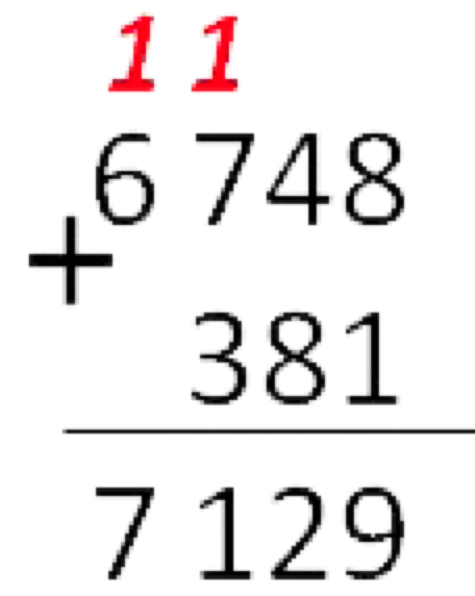
В двоичном представлении чисел операция суммирования будет состоять из тех же действий. Приведем код на языке python:
Теперь попробуем разработать аналогичную программу для квантового вычислителя:

В этой схеме первые два кубита – это аргумент, следующие два – переносы, оставшиеся 3 – результат. Вот как работает алгоритм.
Запустив оба примера, мы получим один и тот же результат. На квантовом компьютере это займет больше времени, потому что необходимо провести дополнительную компиляцию в квантовоассемблерный код и отправить его на исполнение в облако. Использование квантовых вычислений имело бы смысл, если бы скорость выполнения их элементарных операций – гейтов – была бы во много раз меньше чем в классической модели.
Измерения специалистов показывают, что выполнение одного гейта занимает около 1 наносекунды. Так что алгоритмы для квантового вычислителя должны не копировать классические, а по максимуму использовать уникальные свойства квантовой механики. В следующей статье мы разберем одно из основных таких свойств — квантовый параллелизм — и поговорим о квантовой оптимизации в целом. Затем определим наиболее подходящие сферы для квантовых вычислений и расскажем об их применении.
По материалам Дмитрия Сапаева, старшего руководителя направления по развитию ИТ-систем в отделе разработки ЦТИ Сбербанк-Технологий, и Дмитрия Булычкова, директора проектов в Центре технологических инноваций Сбербанка.

Классические вычисления: AND, OR, NOT
Чтобы разобраться с квантовыми вычислениями, стоит для начала освежить знания о классических. Здесь единицей обрабатываемой информации является бит. Каждый бит может находиться только в одном из двух возможных состояний – 0 или 1. Регистр из N бит может содержать одну из 2N возможных комбинаций состояний и представляется в виде их последовательности.
Для обработки и преобразования информации используются побитовые операции, пришедшие из булевой алгебры. Основные операции — это однобитная NOT и двубитные AND и OR. Битовые операции описываются через таблицы истинности. В них приводится соответствие входных аргументов получаемому значению.
Алгоритм классических вычислений — это набор последовательных битовых операций. Удобней всего воспроизводить его графически, в виде схемы из функциональных элементов (СФЭ), где каждая операция имеет свое обозначение. Вот пример СФЭ для проверки двух бит на эквивалентность.

Квантовые вычисления. Физическая основа
А теперь перейдем к новой теме. Квантовые вычисления — это альтернатива классическим алгоритмам, основанная на процессах квантовой физики. Она гласит, что без взаимодействия с другими частицами (то есть до момента измерения), электрон не имеет однозначных координат на орбите атома, а одновременно находится во всех точках орбиты. Область, в которой находится электрон, называется электронным облаком. В ходе известного эксперимента с двумя щелями один электрон проходит одновременно через обе щели, интерферируя при этом с самим собой. Только при измерении эта неопределенность схлопывается и координаты электрона становятся однозначными.

Вероятностный характер измерений, присущий квантовым вычислениям, лежит в основе многих алгоритмов – например, поиск в неструктурированной БД. Алгоритмы данного типа пошагово увеличивают амплитуду правильного результата, позволяя получить его на выходе с максимальной вероятностью.
Кубиты
В квантовых вычислениях физические свойства квантовых объектов реализованы в так называемых кубитах (q-bit). Классический бит может находиться только в одном состоянии – 0 или 1. Кубит до измерения может находиться одновременно в обоих состояниях, поэтому его принято обозначать выражением a|0? + b|1?, где A и B — комплексные числа, удовлетворяющие условию |A|2+|B|2=1. Измерение кубита мгновенно «схлопывает» его состояние в одно из базисных – 0 или 1. При этом «облако» коллапсирует в точку, первоначальное состояние разрушается, и вся информация о нем безвозвратно теряется.

Одно из применений этого свойства –
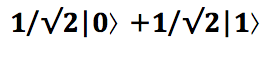
Квантовые и классические вычисления. Первый раунд
Начнем с основ. Имеется набор исходных данных для вычислений, представленный в двоичном формате векторами длиной N.
В классических вычислениях в память компьютера загружается только один из 2n вариантов данных и для этого варианта вычисляется значение функции. В результате одновременно обрабатывается только один из 2n возможных наборов данных.
В памяти квантового компьютера одновременно представлены все 2n комбинации исходных данных. Преобразования применяются ко всем этим комбинациям сразу. В результате за одну операцию мы вычисляем функцию для всех 2n возможных вариантов набора данных (измерение в итоге все равно даст только одно решение, но об этом позже).
И в классических, и в квантовых вычислениях используются логические преобразования — гейты. В классических вычислениях входные и выходные значения хранятся в разных битах, а значит в гейтах количество входов может отличаться от количества выходов:

Рассмотрим реальную задачу. Нужно определить, эквивалентны ли два бита.
Если при классических вычислениях на выходе получаем единицу, значит эквивалентны, иначе нет:

Теперь представим эту задачу с помощью квантовых вычислений. В них все гейты преобразований имеют столько же выходов, сколько входов. Это связано с тем, что результатом преобразования является не новое значение, а изменение состояния текущих.

В примере мы сравниваем значения первого и второго кубитов. Результат будет в нулевом кубите — кубите-флаге. Данный алгоритм применим только к базовым состояниям – 0 или 1. Вот порядок квантовых преобразований.
- Воздействуем на кубит-флаг гейтом «Не», выставляя его в 1.
- Два раза применяем двухкубитный гейт «Контролируемое Не». Этот гейт меняет значение кубита-флага на противоположное только в случае, если второй кубит, участвующий в преобразовании, находится в состоянии 1.
- Измеряем нулевой кубит. Если в результате получили 1, значит и первый, и второй кубиты либо оба в состоянии 1 (кубит-флаг два раза поменял свое значение), либо в состоянии 0 (кубит-флаг так и остался в состоянии 1). Иначе кубиты находятся в разных состояниях.
Следующий уровень. Квантовые однокубитные гейты Паули
Попробуем сравнить классические и квантовые вычисления в более серьезных задачах. Для этого нам потребуется еще немного теоретических знаний.
В квантовых вычислениях обрабатываемая информация закодирована в квантовых битах – так называемых кубитах. В простейшем случае кубит, как и классический бит, может находиться в одном из двух базисных состояний: |0? (краткое обозначение для вектора 1|0? + 0|1?) и |1? (для вектора 0|0? + 1|1?). Квантовый регистр представляет собой тензорное произведение векторов кубит. В простейшем случае, когда каждый кубит находится в одном из базисных состояний, квантовый регистр эквивалентен классическому. Регистр из двух кубит, находящихся в состоянии |0>, можно расписать в таком виде:
(1|0? + 0|1?)*(1|0? + 0|1?) = 1|00? + 0|01? + 0|10? + 0|11? = |00?.
Для обработки и преобразования информации в квантовых алгоритмах используются так называемые квантовые вентили (гейты). Они представляются в виде матрицы. Для получения результата применения гейта, нам необходимо умножить вектор, характеризующий кубит, на матрицу гейта. Первая координата вектора – множитель перед |0?, вторая координата – множитель перед |1?. Матрицы основных однокубитных гейтов выглядит так:

А вот пример применения гейта Not:
X * |0? = X * (1|0? + 0|1?) = 0|0? + 1|1? = |1?
Множители перед базисными состояниями называются амплитудами и являются комплексными числами. Модуль комплексного числа равен корню из суммы квадратов действительной и мнимой частей. Квадрат модуля амплитуды, стоящей перед базисным состоянием, равен вероятности получить это базисное состояние при измерении кубита, поэтому сумма квадратов модулей амплитуд всегда равна 1. Мы могли бы использовать произвольные матрицы для преобразований над кубитами, но из-за того, что норма (длина) вектора всегда должна быть равна 1 (сумма вероятностей всех исходов всегда равна 1), наше преобразование должно сохранять норму вектора. Значит преобразование должно быть унитарным и соответствующая ему матрица унитарной. Напомним, что унитарное преобразование обратимо и UU†=I.
Для более наглядной работы с кубитами их изображают векторами на сфере Блоха. В такой интерпретации однокубитные гейты представляют собой вращение вектора кубита вокруг одной из осей. Например гейт Not (X) поворачивает вектор кубита на Pi относительно оси X. Таким образом, состояние |0>, представляемое вектором, направленным строго вверх, переходит в состояние |1>, направленное строго вниз. Состояние кубита на сфере Блоха определяется формулой cos(?/2)|0?+ei?sin(?/2)|1?

Квантовые двухкубитные гейты
Для построения алгоритмов нам недостаточно только однокубитных гейтов. Необходимы гейты, которые осуществляют преобразования в зависимости от некоторых условий. Основным таким инструментом является двухкубитный гейт CNOT. Этот гейт применяется к двум кубитам и инвертирует второй кубит только в том случае, если первый кубит находится в состоянии |1?. Матрица гейта CNOT выглядит так:
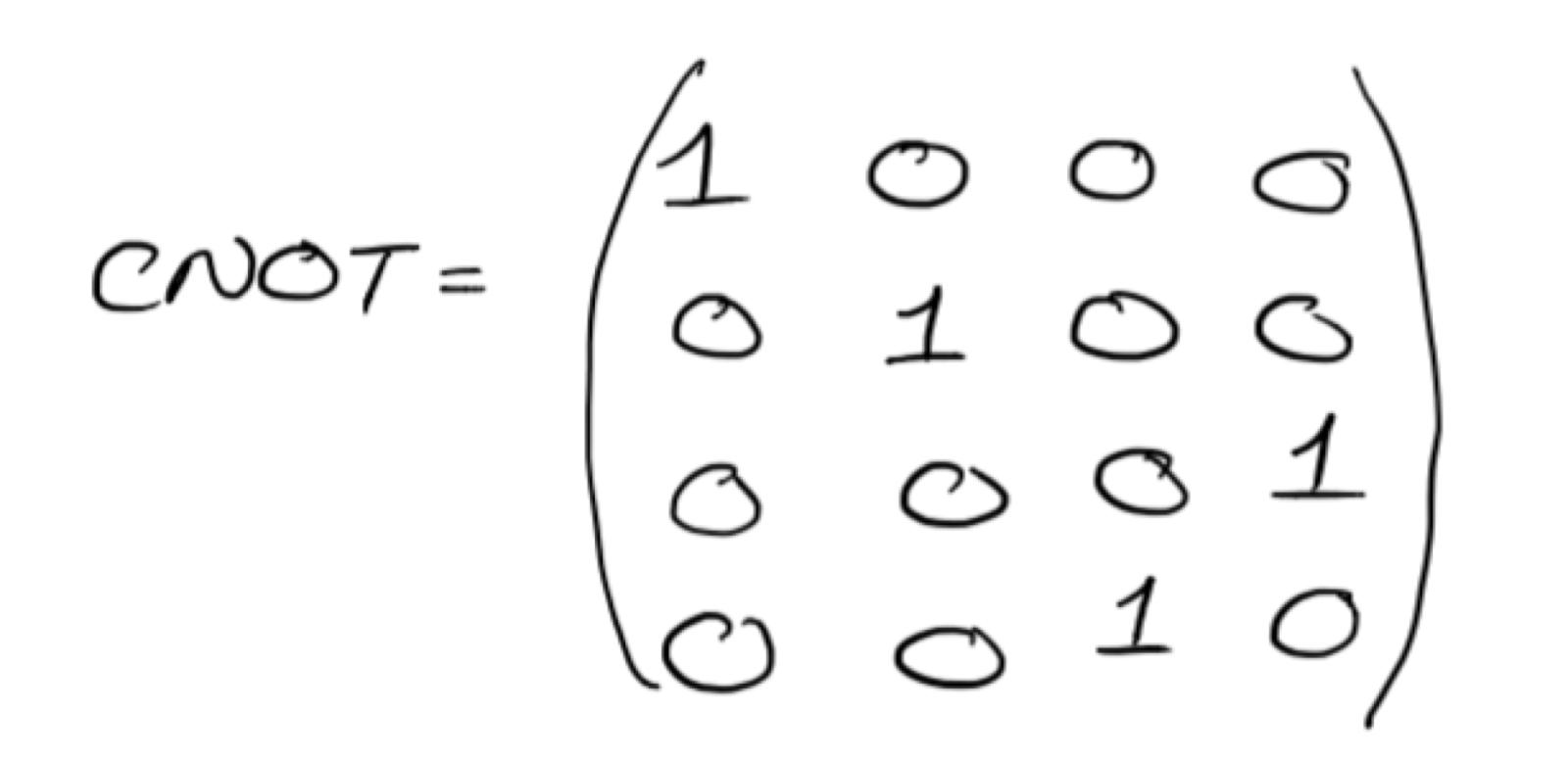
А вот пример применения:
CNOT *|10? = CNOT * (0|00? + 0|01? + 1|10? + 0|11?) = 0|00? + 0|01? + 1|11? + 0|10? = |11?
Применение гейта CNOT эквивалентно выполнению классической операции XOR с записью результата во второй кубит. Действительно, если посмотреть на таблицу истинности оператора XOR и CNOT, то увидим соответствие:
| XOR |
CNOT |
|||
| 0 |
0 |
0 |
00 |
00 |
| 0 |
1 |
1 |
01 |
01 |
| 1 |
0 |
1 |
10 |
11 |
| 1 |
1 |
0 |
11 |
10 |
У гейта CNOT есть интересное свойство – после его применения кубиты запутываются или распутываются, в зависимости от исходного состояния. Это будет показано в следующей статье, в разделе про квантовый параллелизм.
Построение алгоритма — классическая и квантовая реализация
Имея полный арсенал квантовых гейтов, мы можем приступать к разработке квантовых алгоритмов. В графическом представлении кубиты представляются прямыми линиями – «струнами», на которые накладываются гейты. Однокубитные гейты Паули обозначаются обычными квадратами, внутри которых изображается ось вращения. Гейт CNOT выглядит немного сложнее:

Пример применения гейта CNOT:

Одним из важнейших действий в алгоритме является измерение полученного результата. Измерение обычно обозначается дуговой шкалой со стрелкой и обозначением, относительно какой оси идет измерение.
Итак, попробуем построить классический и квантовый алгоритм, который прибавляет 3 к аргументу.
Суммирование обычных чисел столбиком подразумевает совершение двух действий над каждым разрядом – сумму самих цифр разряда и сумму результата с переносом с предыдущей операции, если таковой перенос был.
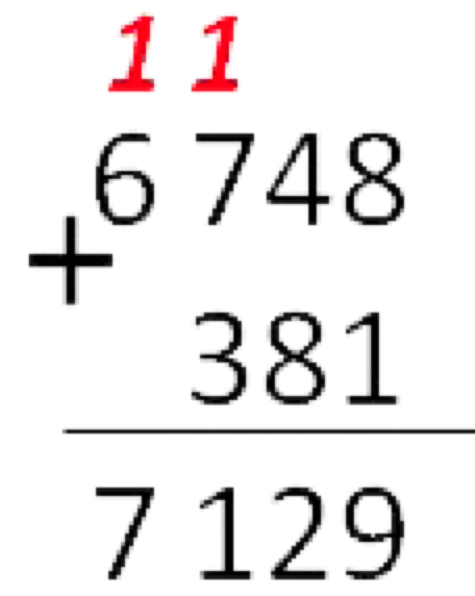
В двоичном представлении чисел операция суммирования будет состоять из тех же действий. Приведем код на языке python:
arg = [1,1] #задаем аргумент
result = [0,0,0] #инициализируем результат
carry1 = arg[1] & 0x1 #складываем с 0b11, так что перенос от младшего бита появится в том случае, если у агрумента младший бит = 1
result[2] = arg[1] ^ 0x1 #складываем младшие биты
carry2 = carry1 | arg[0] #складываем с 0b11, так что перенос от старшего бита появится в том случае, если у агрумента старший бит = 1 или был перенос с младшего бита
result[1] = arg[0] ^ 0x1 #складываем старшие биты
result[1] ^= carry1 #применяем перенос с младшего бита
result[0] ^= carry2 #применяем перенос со старшего бита
print(result)Теперь попробуем разработать аналогичную программу для квантового вычислителя:

В этой схеме первые два кубита – это аргумент, следующие два – переносы, оставшиеся 3 – результат. Вот как работает алгоритм.
- Первым шагом до барьера мы выставляем аргумент в то же состояние, как и в классическом случае – 0b11.
- С помощью оператора CNOT вычисляем значение первого переноса – результат операции arg & 1 равен единице только тогда, когда arg равен 1, в этом случае мы инвертируем второй кубит.
- Следующие 2 гейта реализуют сложение младших бит – мы переводим кубит 4 в состояние |1? и результат XOR записываем в него же.
- Большим прямоугольником обозначен гейт CCNOT – расширение гейта CNOT. В этом гейте два управляющих кубита и третий инвертируется только в том случае, если первые два находятся в состоянии |1. Комбинация из 2 гейт CNOT и одного CCNOT дает нам результат классической операции carry2 = carry1 | arg[0]. Первые 2 гейта выставляют перенос в единицу в том случае, если один из них равен 1, а гейт CCNOT обрабатывает случай, когда они оба равны единице.
- Складываем старшие кубиты и кубиты переноса.
Промежуточные выводы
Запустив оба примера, мы получим один и тот же результат. На квантовом компьютере это займет больше времени, потому что необходимо провести дополнительную компиляцию в квантовоассемблерный код и отправить его на исполнение в облако. Использование квантовых вычислений имело бы смысл, если бы скорость выполнения их элементарных операций – гейтов – была бы во много раз меньше чем в классической модели.
Измерения специалистов показывают, что выполнение одного гейта занимает около 1 наносекунды. Так что алгоритмы для квантового вычислителя должны не копировать классические, а по максимуму использовать уникальные свойства квантовой механики. В следующей статье мы разберем одно из основных таких свойств — квантовый параллелизм — и поговорим о квантовой оптимизации в целом. Затем определим наиболее подходящие сферы для квантовых вычислений и расскажем об их применении.
По материалам Дмитрия Сапаева, старшего руководителя направления по развитию ИТ-систем в отделе разработки ЦТИ Сбербанк-Технологий, и Дмитрия Булычкова, директора проектов в Центре технологических инноваций Сбербанка.
Комментарии (8)

bukov_georgiy
28.11.2017 19:12-1Всегда, когда на IT-ресурсах читаю про квантовые компьютеры, сталкиваюсь со следующим: пишут поверхностно про алгоритмы, парадоксы и т.д. (забывая указать неправильность постановки эксперимента, например), но не пишут про инженерное исполнение. Серьезно, почему бы спецам по IT и инженерам не писать про физическую реализацию, а алгоритмы оставить математикам? Смешно выходит, ни в пи***, ни в красную армию.


maslyaev
Как-то у меня придумался квантовый алгоритм поиска кратчайшего пути в графе. Дешёвый и сердитый. На элементной базе, доступной любому приверженцу DIY. Берём паяльник, провода и набор маломощных резисторов. Распаиваем схему, в которой вес пути кодируем сопротивлением резистора. Врубаем 220 на точки, между которыми ищем путь. Где задымилось — там кратчайший путь. Быстродействие — потрясающее, полный параллелизм.
Шутка. Не воспринимайте, пожалуйста, всерьёз.
lolhunter
Вы изобрели аналоговый компьютер.
Им на самом деле можно было решать некоторые задачи фактически без вычислений.
Были даже на воде.
maslyaev
Велосипедостроение живо до тех пор, пока люди не перестают снова и снова изобретать велосипед.
Кстати, замутить решатель задачи коммивояжёра на чём-нибудь аналоговом — это было бы интересно.
lolhunter
В принципе теоретически можно. Проблема только в размерах, которые растут экспоненциально от добавления точек. Ведь надо соединить «города» по топологии «каждый с каждым».
ARad
У вас задымиться в самом напряженном месте, кратчайший путь с ним никак не связан.
gban
ну да, относительно маломощный резистор…
maslyaev
Задымится там, где по максимуму I*V. Т.е. рассеиваемая мощность.