Из статьи по одномерным мирам вы знаете, что одномерным мир делает то, что положение в нём определяется одной единицей информации.

Также он должен быть непрерывным (или близким к непрерывному с практической точки зрения). Я описал несколько примеров размерностей: доходная линия, бесконечная, и представленная бесконечной прямой; радужная линия, конечная, с ограничивающими стенами, представленная отрезком; эолова линия направлений ветра, конечно-периодическая, представленная отрезком, у которого левый конец совпадает с правым, или, что то же самое, кругом. Вскользь я упомянул об ещё одном примере — о мире, бесконечном в одном направлении, и конечном в другом. В другой статье я сделал упор на то, что типов измерений бывает много, но у физических измерений пространства существуют уникальные и особые (а также весьма очевидные) свойства, отличающие их от измерений другого типа.


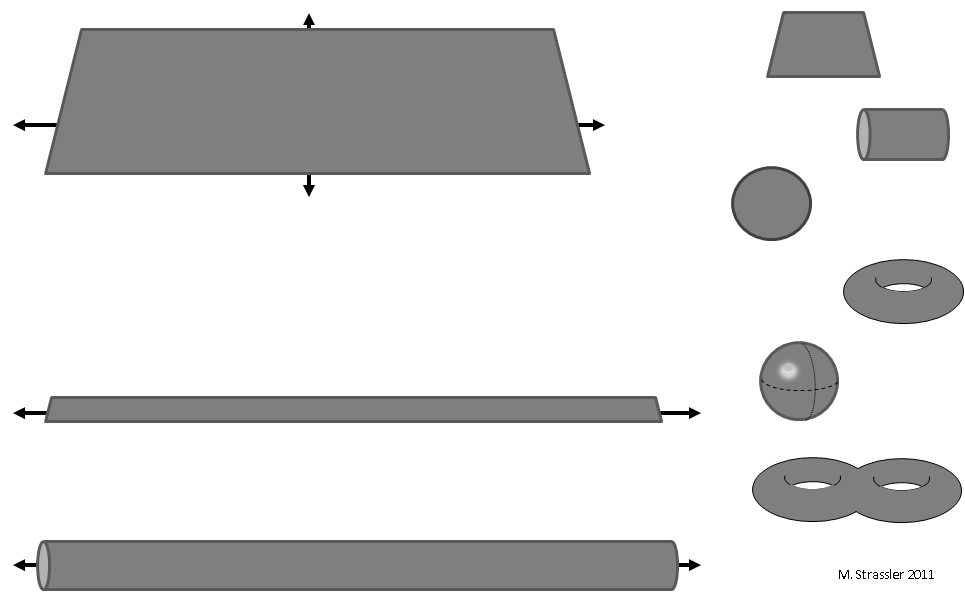
Рис. 1: двумерные миры

Что же насчёт двумерных миров? Неудивительно, что типов двумерных миров бывает много больше, чем типов одномерных миров. Несколько примеров таких пространств показано на рис. 1. Можно представить мир, бесконечный в обоих направлениях: плоскость (слева вверху). Можно представить мир, бесконечный в одном направлении, а в другом формирующий либо отрезок, либо круг. Такие миры естественным образом называются полоской и трубой (слева внизу). Можно представить мир конечный в обоих направлениях (правая часть рис. 1). И сколько тут возможностей! Только на этом рисунке можно увидеть сверху вниз квадрат, цилиндр (круглая часть банки без крышек и внутренности), диск, тор (нечто вроде автомобильной шины), сферу (только поверхность), двойную шину. И это не все варианты. Если экстраполировать в будущее, становится ясно, что к моменту, когда мы доберёмся до трёх измерений, и пойдём дальше, мы уже будем не в состоянии составлять такие списки.

Как и с одномерными пространствами, положение в двумерном пространстве определяется двумя единицами информации.

Примером сферы (с хорошим приближением) может быть поверхность Земли: любое местоположение можно обозначить широтой и долготой. Муравей, шагающий по садовому шлангу, движется вдоль двумерной трубы, и в любой момент времени расположен на определённом расстоянии от крана и под определённым углом к вертикали. Многополосное шоссе, по сути, представляет собой двумерную полоску с очень длинной стороной и короткой стороной: две единицы информации, необходимые для определения вашего положения, это расстояние с начала дороги и расстояние от её правого края.

Вспомним доходную линию. «Ваш доход за прошлый год — это определённое число в вашей местной валюте. Он может быть положительным или отрицательным, большим или маленьким; его можно представить как точку на линии, как на рис. 1, которую мы будем называть «точкой дохода». Каждая точка на линии представляет возможный доход». Если вы состоите в браке, и доходы есть и у вас, и у вашего супруга, два входящих в ваше домашнее хозяйство денежных потока можно представить в виде двухдоходной плоскости. Два числа, описывающих точку на этой плоскости, будут вашим доходом и доходом вашего супруга.

А вот хитрый пример тора, показывающей, как можно представлять себе интересные двумерные формы, чьи измерения не являются измерениями физического пространства. На рис. 3 статьи об одномерных мирах мы видели, что возможные направления ветра формируют одномерный мир в виде круга (или линии, у которой совпадают начало и конец). Возможные направления движения парусной лодки тоже формируют похожий круг. Но все, кто ходил под парусом, знают, что не обязательно двигаться в том же направлении, в каком дует ветер; если поставить парус под углом, можно двигаться на запад, даже если ветер дует с севера. Так что если я запрошу две единицы информации — с какого направления дует ветер, и в каком направлении движется моя парусная лодка — обе они будут точками на круге. Две единицы информации, обе расположенные на круге, обозначают точку на торе.

Перед тем, как продолжить, упомяну естественную и распространённую путаницу. Я уже намекал на неё в описании различных миров, данных выше. Не нужно путать измерения самих форм с определённым способом представления этих измерений или форм! Свойство круга таково, что если вы двигаетесь по нему в любом направлении, вы вернётесь туда, откуда начали. У круга нет ничего внутри или снаружи. Просто представление круга в виде замкнутой кривой на двумерной плоскости выглядит так, будто у него есть внутренняя и внешняя часть. Но это просто свойство представления круга на плоскости, а не свойство самого круга.