Рис. 1: мелкая лодка в канале может двигаться вдоль и поперёк

Пора узнать что-либо при помощи двумерного пространства, что мы не могли узнать, используя одномерное. В частности давайте обратимся к полоске — пространству, которое выглядит, как лента, с одним очень длинным измерением (возможно, бесконечным), и одним очень коротким. Большая часть того, что относится к полоске, будет справедливо и для трубы, но я ограничусь полоской, поскольку её легче рисовать.

Во-первых, позвольте напомнить концепцию, введённую мной в конце статьи про одномерные миры. Даже если какой-либо физический мир трёхмерен, например, наш с вами привычный мир, для определённых его аспектов возможно вести себя так, будто они одномерные. К примеру, человек, идущий по канату, существует в трёх измерениях, но его движения будут по сути одномерными. В этом случае его мир делают одномерным ограничения, необходимые для его безопасности. На полоске же у нас есть ещё одна причина для того, почему этот мир может быть эффективно одномерным. У неё есть большое измерение и малое, и то, можете ли вы двигаться вдоль малого, зависит от вашей формы и размера по сравнению с расстоянием, описывающим малое измерение.

Вот вам пример полоски: судоходный канал. Длинная полоса воды позволяет мелкой лодке двигаться в двух измерениях: она может двигаться по каналу вверх и вниз, или поперёк него, вперёд и назад. Но гигантское грузовое судно, едва помещающийся в канале, способен двигаться только вперёд или назад. Для грузового судна канал эффективно одномерный. Если бы вы наблюдали за его движением, вы бы не нашли признаков двухмерности канала. Движение крупного объекта — крупного по сравнению с шириной полоски — обнаруживает для нас длинное измерение, но не даёт признаков второго, короткого; второе измерение открывается лишь движением мелкого объекта, такого, как маленькая лодка. Это очень важный урок!


Рис. 2: гигантское грузовое судно может двигаться по каналу только вперёд и назад

Ещё один пример того же самого? Для нас с вами поверхность человеческого волоса, по сути, одномерный объект, если смотреть на него невооружённым глазом. Волос можно разрезать на два кусочка в два раза меньшей длины, но нам будет очень трудно разрезать волос вдоль: в английском даже существует такое понятие, как «расщеплять волосы», обозначающее деятельность, не стоящую времени и усилий. Но крохотный пылевой клещ способен ползать по поверхности волоса так, будто это гигантская труба. Для клеща поверхность волоса кажется двумерной, так, как для нас двумерной выглядит поверхность флагштока.

Вернёмся к грузовому судну. Представьте, что это судно было бы разумным существом, с мозгом, получающим информацию от органов чувств, как это происходит у животных, но с единственным органом чувств, позволяющим ему определять только собственное движение.

Зачем я обращаюсь к сознанию? Оно не имеет никакого значения для пространственных измерений, которые мы обсуждаем — они есть вне зависимости от того, есть ли сознание у судна, или нет. Я пытаюсь объяснить вам, как разумное существо — такое, как вы — может быть введено в заблуждение своими органами чувств и мозгом по поводу истинных свойств природы, и может не иметь представления о пространственных измерениях.

Единственная информация, идущая из такого органа чувств в мозг судна, будет нечто вроде «вперёд со скоростью пять километров в час» или «назад со скоростью двух километров в час» или «неподвижен» [на воде скорость обычно измеряется в узлах, т.е. морских милях в час; кроме того, существует разница скоростей относительно поверхности воды и относительно дна. Но в данном случае этим можно пренебречь / прим. перев.]. Какую картину мира построил бы мозг судна? Без всякой информации, поступающей снаружи по поводу присутствия второго измерения поперёк полосы, он, естественно, создал бы одномерную картину мира, в которой у канала было одно измерение. У судна не было бы информации о втором измерении, хотя его легко обнаружила бы мелкая лодка.


Контейнеровоз проходит Панамский канал

Это один из примеров того, как могут работать «дополнительные измерения» (но не единственный, как мы позже увидим). Под «дополнительным» подразумевается, что это измерение, о существовании которого грузовое судно не знало и не могло знать, учитывая его органы чувств.

Теперь представьте, что нечто подобное применимо и к нам. Допустим, мы живём в полоске, у которой в дополнение к трём крупным пространственным измерениям, в рамках которых мы обычно двигаемся, которые распознаём органами чувств и представляем в голове, существует ещё и четвёртое пространственное измерение, настолько невероятно малое, что мы заполняем его, как грузовое судно, и не можем в нём двигаться. Более того, наши органы зрения, слуха, осязания, обоняния или вкуса не способны обнаружить присутствие этого дополнительного измерения. Насколько известно нашему мозгу, его там нет. Но может, на самом деле, оно там есть, и достаточно мелкие существа могли бы двигаться вдоль него и ощущать его.

Предположение о существовании одного или нескольких дополнительных измерений — это всего лишь рассуждение, чистый вымысел. Нам неизвестно, истинно ли оно. Но я пытаюсь объяснить вам, что нам неизвестно, что оно ложно.

Так что следующий вопрос такой: могут ли люди-учёные, чьи чувства и мозги не способны различить четвёртое измерение пространства, найти его? Именно в этот момент вступает смесь человеческого интеллекта и передовых научных инструментов.

Как мы увидим далее, исследования показывают, что, хотя одно или несколько дополнительных измерений такого типа и могут существовать в природе, они должны быть чрезвычайно малыми. Поперечный размер такого измерения не может быть больше, чем 1/10 000 диаметра протона, или 1/1 000 000 000 диаметра атома, или 0,000 000 000 000 000 000 1 метра. Исследования, проводимые на Большом адронном коллайдере, постепенно подбираются к этому размеру.

Ещё один пример

Пример дополнительного измерения, описанный выше, является только одним из нескольких общих возможностей. Вот вам ещё пример. Вместо судна с огромной шириной, занимающей весь канал, рассмотрим более узкое судно, прочно пришвартованное к одной стороне канала так, что хотя, в принципе, оно может двигаться поперёк канала, на практике у него это не получится. Взаимоотношения между лодкой и дополнительным измерением другие, но эффект от этого — то, что малое измерение двухмерного канала нельзя обнаружить по движению лодки — такой же.


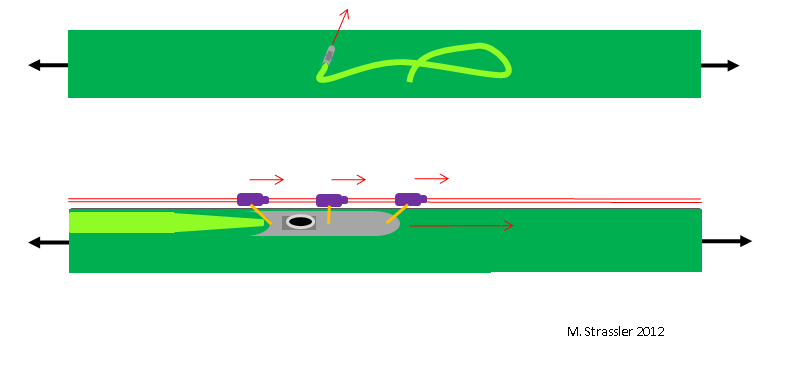
Рис. 3

Конкретнее, представим себе лодку, которая, как на рис. 3, двигается вперёд или назад вдоль канала, используя как свой двигатель, так и помощь средств передвижения, движущихся по рельсам вдоль канала — современная форма бечевника. В отличие от крупного контейнеровоза, эта лодка не заполняет всю ширину канала. В принципе она могла бы двигаться поперёк канала, от одной его стороны к другой. Но на практике существуют силы — оказываемые канатами, связывающими её с передвигающимися по рельсам устройствами — удерживающие её у левой стены канала. И эти силы настолько сильны, что лодка никогда не отходит от левой стены. И поскольку она двигается вперёд и назад вдоль канала, её движение сугубо одномерное. Как и с крупным судном, мы можем представить себе, что если бы эта лодка обладала сознанием, и её чувства давали бы ей только информацию о её движении, её мозг создал бы одномерную картину канала, несмотря на то, что если перерубить верёвки, лодка могла бы поворачиваться и передвинуться к центру, или даже к правой стене канала!

То же справедливо и для нас. Мы — точнее, каждая частица, из которых состоит наше тело, и всё, что мы можем видеть, чувствовать, обнаруживать при помощи современных научных инструментов — может быть присоединено силами чрезвычайной величины, которые мы не можем преодолеть, и о которых мы не имеем представления, к трёхмерной стене пространства с четырьмя пространственными измерениями. И, поскольку наши движения ограничены стеной, и наши чувства регистрируют только объекты, ограниченные ею сходным образом, наш мозг строит для нас трёхмерную картину мира, несмотря на то, что на самом деле в нашем мире есть дополнительное измерение.

Опять-таки, нет никаких гарантий, что это на самом деле так. Это всё чистые рассуждения. Но мы не можем быть уверены в том, что это не так. Единственный способ это выяснить — разработать и провести научные эксперименты, чью природу я вскоре объясню. Оказывается (как было показано, ко всеобщему шоку и недоверию, в знаменитой работе от 1999 года за авторством Нима Аркани-Хамеда, Саваса Димополуса и Гии Двали), что это дополнительное измерение второго типа может быть гораздо больше того, что я описывал ранее — возможно, настолько большое, как ширина человеческого волоса! (На самом деле, когда эта работа была написана, эксперименты всё ещё не запрещали дополнительным измерениям иметь размеры до миллиметра. Но с тех пор были проведены новые, и они наложили новые ограничения на эту возможность.) И это удивительно. Несмотря на все эксперименты, проводимые при помощи микроскопов и крохотного электронного оборудования, встроенного в наши компьютеры, мы всё ещё можем не знать о существовании дополнительного измерения небольшого, но всё-таки макроскопического размера.

Ещё примеры

Когда мы начинаем рассуждать в подобном направлении, мы можем найти ещё больше возможностей, чем описанные две.

К примеру, нет причин для того, чтобы не существовало больше одного дополнительного измерения. Пример мы можем привести с использованием нашего судового канала — ведь если он достаточно глубокий, о нём можно рассуждать, как о трёхмерном, очень длинном в одном направлении, но конечной ширины и глубины. Тогда мы можем придумать множество разных объектов, для которых канал обладает нулём, одним или двумя дополнительными короткими измерениями, как показано на рис. 4


Рис. 4

Подводная лодка может двигаться в канале по трём измерениям. Небольшая лодка привязана к двумерной поверхности канала, и двигается, не имея понятия о том, что у канала есть глубина [в реальности к шкиперу лодки, не имеющему понятия о глубине канала, возникают различные вопросы / прим. перев.]. Её двумерное восприятие мира не учитывает одного дополнительного измерения. А три различных типа судов не будут знать о двух из трёх измерений. Один пример — лодка на буксире, привязанная к стене и поверхности. Другой пример — широкая баржа, заполняющая канал на всю ширину, и привязанная к поверхности. И, наконец, третий пример — гигантское судно, достигающее килем канала, и, по сути, заполняющее его целиком. По трём совершенно разным причинам движение трёх этих судов не обнаруживало бы никаких признаков глубины и ширины канала, и, если бы они были мыслящими существами, они могли бы с удивлением узнать о том, что в их мире есть два дополнительных измерения.