Геометрическое доказательство теоремы Пифагора
Вокруг да около
История теоремы Пифагора уходит в века и тысячелетия. В этой статье, мы не будем подробно останавливаться на исторических темах. Для интриги, скажем только, что, по-видимому, эту теорему знали еще древне-египетские жрецы, жившие более 2000 лет до нашей эры. Для тех, кому любопытно, вот ссылка на статью в Википедии.
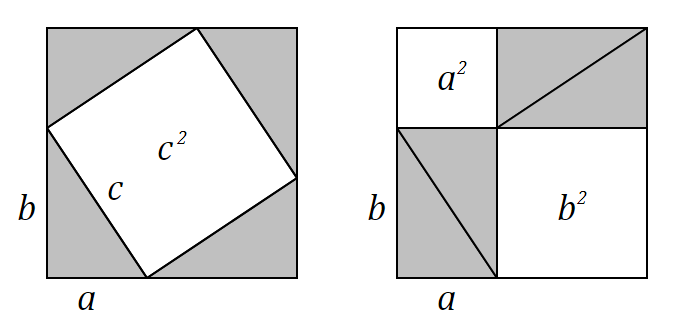
Прежде всего, хочется для полноты изложения привести здесь доказательство теоремы Пифагора, которое, по моему мнению, наиболее элегантно и очевидно. На рисунке выше изображено два одинаковых квадрата: левый и правый. Из рисунка видно, что слева и справа площади закрашенных фигур равны, так как в каждом из больших квадратов закрашено по 4 одинаковых прямоугольных треугольника. А это означает, что и незакрашенные (белые) площади слева и справа тоже равны. Замечаем, что в первом случае площадь незакрашенной фигуры равна , а во втором — площадь незакрашенной области равна . Таким образом, . Теорема доказана!
Зарождение идеи
В этой статье я хочу не только рассказать что-то новое и познавательное о теореме Пифагора, но и поделиться своей историей о том, как в моей голове зародилась интересная идея, которую я сумел сформулировать, доказать и даже предположил возможность обобщения на более высокую размерность. Но обо всем по порядку.
Египетские треугольники
С давних времен науке известны так называемые египетские треугольники. Это такие прямоугольные треугольники, у которых катеты и гипотенуза выражаются целыми числами. Можно сказать и иначе: египетские треугольники — это такие тройки натуральных чисел , которые образуют прямоугольный треугольник. Мы все, наверняка, хоть раз встречались с ними в школе на уроках геометрии. Для примера привожу несколько таких троек:
Во-первых, это красивые математические объекты. А во-вторых, с ними очень удобно решать задачи! Нет никаких квадратных корней и иррациональных чисел в ответе.
Загадочные четверки
И вот, году этак в 2004 — 2005, в пору подготовки к ЕГЭ, когда я сутками напролет решал просто какую-то бесконечную прорву хитро-вычурных задач из части С, мне то и дело стали попадаться не тройки, а уже четверки чисел, которые обладали похожими свойствами: а именно, сумма квадратов трех из них давала полный квадрат четвертого. Этот факт заинтриговал меня настолько, что я до сих пор наизусть помню некоторые из них. На самом деле, таких четверок бесконечно много и только в пределах чисел до 1000 их существует около 84 000. А вот, к примеру, пять таких четверок, из тех, что компьютер нашел перебором, пока я писал эту статью:
Заметив такое удивительное совпадение, я стал думать. Вопрос, который меня занимал в связи с этим загадочным обстоятельством, наличием не только троек, но и четверок, обнаруживающих свойства египетского треугольника, был таков: "А что бы это все могло значить?" Я перебирал варианты, какие только приходили в голову. В фантазии себя никак не ограничивал. Много раз садился за стол, выписывал известные мне наборы четверок и вдумчиво на них смотрел… часами… без перерыва… и… ничего не происходило. У меня был школьный товарищ Саня, с которым я как-то поделился своими идеями. Но его больше интересовали гуманитарные науки. Он стал юристом и сейчас служит в звании майора милиции. Саня сказал мне примерно следующее:«Вот странный ты человек. Делать тебе больше нечего. Мало тебе задают домашек? Хватит думать о всякой ерунде!». А, надо сказать, думал я, не переставая, и думал много лет, время от времени возвращаясь к этой загадке. Еще будучи школьником, я сделал вывод, что это, вероятнее всего, имеет отношение к великой теореме Ферма (на которую я тоже много раз подолгу смотрел). Шли годы. Ничего не получалось. Озарение не приходило. И я понял, что, вероятно, дальше чем «что-то связанное с теоремой Ферма» я никуда уже не продвинусь. Но не тут то было
Шерлок нашел зацепку
Итак, в 2014 году ехал я в автобусе по Новосибирску. А может быть это было метро. Дорога не близкая. Заняться нечем. И в очередной раз решил я подумать о моей школьной загадке. И вот что я подумал.
Как же назвать эти числа? Треугольниками не назовешь, ведь четыре числа никак не могут образовать треугольник. И тут! Как гром среди ясного неба
Раз есть такие четверки чисел, значит должен быть геометрический объект с такими же свойствами, отраженными в этих числах!
Теперь осталось только подобрать какой-то геометрический объект под это свойство, и все встанет на свои места! Конечно, предположение было чисто гипотетическое, и никакого подтверждения под собой не имело. Но что если это так!
Начался перебор объектов. Звезды, многоугольники, правильные, неправильные, с прямым углом и так далее и тому подобное. Опять ничего не подходит. Что делать? И в этот момент Шерлок получает свою вторую зацепку.
Надо повысить размерность! Раз тройке соответствуют треугольник на плоскости, значит четверке соответствует нечто трехмерное!
О нет! Опять перебор вариантов! А в трехмерии гораздо, гораздо больше всевозможных геометрических тел. Попробуй перебрать их все! Но не все так плохо. Есть же еще прямой угол и другие зацепки! Что мы имеем? Египетские четверки чисел (пусть будут египетские, надо же их как-то называть), прямой угол (или углы) и некий трехмерный объект. Дедукция сработала! И… Полагаю, что догадливые читатели уже поняли, что речь идет о пирамидах, у которых при одной из вершин все три угла — прямые. Можно даже назвать их прямоугольными пирамидами по аналогии с прямоугольным треугольником.
Новая теорема
Итак, у нас есть все что нужно. Прямоугольные (!) пирамиды, боковые грани-катеты и секущая грань-гипотенуза. Пришло время нарисовать еще одну картинку.
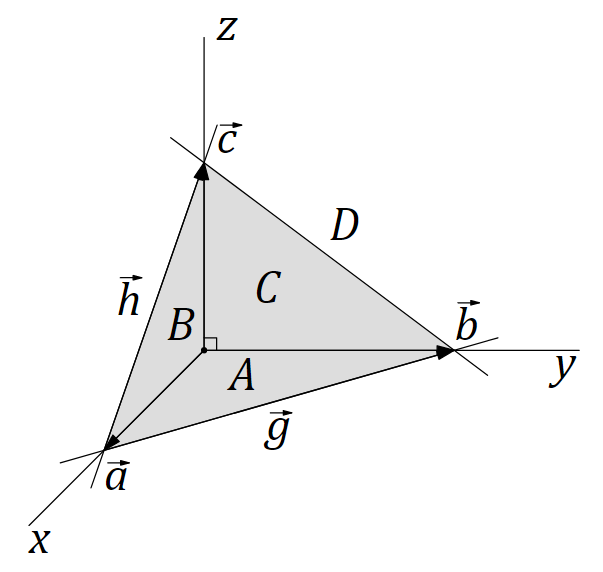
Теорема Пифагора для прямоугольной пирамиды
На картинке изображена пирамида с вершиной в начале прямоугольных координат (пирамида как бы лежит на боку). Пирамида образована тремя взаимно-перпендикулярными векторами, отложенными из начала координат вдоль координатных осей. То есть каждая боковая грань пирамиды — это прямоугольный треугольник с прямым углом при начале координат. Концы векторов определяют секущую плоскость и образуют грань-основание пирамиды.
Теорема
Пусть есть прямоугольная пирамида, образованная тремя взаимно-перпендикулярными векторами , у которой площади граней-катетов равны — , и площадь грани-гипотенузы — . Тогда
Альтернативная формулировка: У четырехгранной пирамиды, у которой при одной из вершин все плоские углы прямые, сумма квадратов площадей боковых граней равна квадрату площади основания.
Разумеется, если обычная теорема Пифагора формулируется для длин сторон треугольников, то наша теорема формулируется для площадей сторон пирамиды. Доказать эту теорему в трех измерениях очень просто, если вы немного знаете векторную алгебру.
Доказательство
Выразим площади через длины векторов .
где .
Площадь представим как половину площади параллелограмма, построенного на векторах и
Как известно, векторное произведение двух векторов — это вектор, длина которого численно равна площади параллелограмма, построенного на этих векторах.
Поэтому
Таким образом,
Что и требовалось доказать!
ЭВРИКА!
Моему восторгу не было границ! Я буквально прыгал от счастья. Конечно, это не бог весть какая сложная теорема, и доказательство очень простое, но ведь сам. И до меня — никто! Я был в этом искренне убежден в течение около года. Попытки найти хоть какие-то свидетельства о том, что это уже известно и доказано терпели неудачу одна за другой, и я думал, что совершил открытие. Это непредаваемое чувство! Я хотел поделиться этой теоремой со всем миром. Говорил о ней друзьям, знакомым математикам, просто знакомым с техническим/математическим образованием и без. Никто не разделял моего восторга и энтузиазма. Всем было попросту безразлично. Будто бы я не придумал и доказал теорему, а просто в магазин за хлебом сходил. Ну и что тут такого? Вот уж действительно… Как говорится, «Как скучно мы живём! В нас пропал дух авантюризма, мы перестали лазить в окна к любимым женщинам, мы перестали делать большие хорошие глупости.» (из фильма «Ирония судьбы»).
Конечно, как у человека, профессионально занимающегося исследованиями, подобное в моей жизни уже случалось, и не раз. Но этот момент был самым ярким и самым запоминающимся. Я испытал полную гамму чувств, эмоций, переживаний первооткрывателя. От зарождения мысли, кристализации идеи, нахождения доказательства — до полного непонимания и даже неприятия, которое встретили мои идеи у моих друзей, знакомых и, как мне тогда казалось, у целого мира. Это было уникально! Я словно почувствовал себя в шкуре Галлилея, Коперника, Ньютона, Шредингера, Бора, Эйнштейна и многих многих других открывателей.
Послесловие
В жизни, все оказалось гораздо проще и прозаичнее. Я опоздал… Но на сколько! Всего-то навсего 18 лет! Под страшными продолжительными пытками и не с первого раза Гугл признался мне, что эта теорема была опубликована в 1996 году!
Вот ссылка на статью:
Amir-Moez, Ali R., Robert E. Byerly, and Robert R. Byerly. «Pythagorean theorem in unitary spaces.» Publikacije Elektrotehnickog fakulteta. Serija Matematika (1996): 85-89.
Статья опубликована издательством Техасского технического университета. Авторы, профессиональные математики, ввели терминологию (которая, кстати, во многом совпала с моей) и доказали также и обобщенную теорему справедливую для пространства любой размерности большей единицы. Что же произойдет в размерностях более высоких, чем 3? Все очень просто: вместо граней и площадей будут гиперповерхности и многомерные объемы. А утверждение, конечно, останется все тем же: сумма квадратов объемов боковых граней равна квадрату объема основания, — просто количество граней будет больше, а объем каждой из них станет равен половине произведения векторов-образующих. Вообразить это почти невозможно! Можно только, как говорят философы, помыслить!
Что удивительно, узнав о том, что такая теорема уже известна, я ничуть не расстроился. Где-то в глубине души я подозревал, что вполне возможно, я был не первый, и понимал, что нужно быть всегда к этому готовым. Но тот эмоциониальный опыт, который я получил, зажег во мне искру исследователя, которая, я уверен, теперь уже не угаснет никогда!
P.S.
Эрудированный читатель в комментариях прислал ссылку
Теорема де Гуа
Выдержка из Википедии
В 1783 году теорема была представлена Парижской академии наук французским математиком Ж.-П. де Гуа, однако ранее она была известна Рене Декарту[3] и до него Иоганну Фульгаберу (англ.), который, вероятно, первым открыл её в 1622 году[4]. В более общем виде теорему сформулировал Шарль Тинсо (фр.) в докладе Парижской академии наук в 1774 году[4]
Так что я опоздал не на 18 лет, а как минимум на пару веков!
Источники
Читатели указали в комментариях несколько полезных ссылок. Вот эти и некоторые другие ссылки:
Комментарии (143)

ed007
13.01.2018 17:08+1Из рисунка выше видно, что слева и справа площади закрашенных фигур равны, а значит и незакрашенные площади слева и справа тоже равны.
Почему-то мне не никак видно равенство площадей.
938MeV Автор
13.01.2018 17:12Попробуйте так. Мы взяли два одинаковых квадрата: левый и правый. И вырезали из каждого по 4 одинаковых прямоугольных треугольника двумя разными способами. Из левого вот так, а из правого иначе. А теперь посмотрим чему равны площади оставшихся (белых) фигур.

maxzhurkin
14.01.2018 08:47Один из вариантов: надо обозначить сторону большого квадрата как a+b, с одной стороны представить его площадь как сумму квадрата гипотенузы и четырёх площадей треугольника, а с другой стороны как квадрат его стороны

nikee
14.01.2018 23:52Главное что бы не получилось как здесь:


938MeV Автор
17.01.2018 06:02До сих пор не могу понят, в чем тут подвох. Не подскажете?

Pand5461
17.01.2018 08:44У большого треугольника катеты 5 и 13 — числа взаимно простые. Значит, на верхнем рисунке все разрезы никак не могут проходить ровно по границам клеточек. Например, красный треугольник — если считать, что большой катет ровно 8, то малый будет 5/13?8 = 40/13 ? 3,077.
Так вот за счёт небольших перекрываний вдоль стыков на нижнем рисунке площадь одной клеточки экономится.
Unc1e_Vanya
17.01.2018 13:11+1:) Вот не надо только про невозможность прохождения по границам клеточек. На рисунке всё абсолютно правильно!
Просто нужно пояснить, что БОЛЬШОй треугольник (8х13) — вовсе не треугольник, а четырёхугольник! И во втором случае он более выпуклый, чем в первом.
Визуально это становится понятным, если наложить на треугольник 8х3 сверху треугольник 5х2 — у треугольника 8х3 угол более острый.


f0rk
17.01.2018 11:06+2До сих пор не могу понят, в чем тут подвох. Не подскажете?
Красный и синий треугольники не подобны, а следовательно гипотенуза большого треугольника на самом деле не гипотенуза, и вообще не прямая.
Unc1e_Vanya
17.01.2018 13:32+1… и вообще он не треугольник. :)
Доказательство через (не)подобие — чудесно.

VYudachev
17.01.2018 18:10А из интересного про подвохи и объяснения — прекрасное видео про парадокс Банаха-Тарского

Pand5461
13.01.2018 17:20У меня сразу только ассоциация с длиной n-мерного вектора, заданного координатами, появилась. Что интересно, идея обобщения на гиперплощади граней пирамиды даже никогда не появлялась, потому что уже было в голове «обобщение теоремы Пифагора на n-мерное пространство».

volantrider
13.01.2018 17:25+6Теоре?ма де Гуа — одно из обобщений теоремы Пифагора на старшие размерности.
В 1783 году теорема была представлена Парижской академии наук.
ru.wikipedia.org/wiki/Теорема_де_Гуа
938MeV Автор
13.01.2018 17:26Обалдеть! :) Благодарю!

marsdenden
14.01.2018 09:56Интересно, американцы в курсе, что теорема была за два века до них или считают себя младшими братьями Пифагора?))

Frankenstine
17.01.2018 14:39+1Вы про опубликованное в 1996 году доказательство? Хоть в нём и не упоминается теорема де Гуа, и приводится отдельно её доказательство, сама публикация посвящена обобщению теоремы Пифагора на n-мерное пространство (количество ортогональных векторов), т.е. шире теоремы де Гуа, являющейся частным случаем обобщения при n=3.

gevlichenko
13.01.2018 17:46+1В новосибе нет математических школ/кружков?

938MeV Автор
13.01.2018 17:49Конечно есть. Просто я сам не из Новосибирска, и школу заканчивал в другом городе за МКАДом :) Мы всё больше по части физики…

32seph
13.01.2018 19:10Ну так и какая связь с теоремой Ферма?

938MeV Автор
13.01.2018 19:12Ах да. Из статьи непонятно. Никакой очевидной связи я не нашел. Кто знает, может быть она в действительности есть.

Pshir
13.01.2018 23:45Точно нет связи.

Keyten
14.01.2018 01:20Вы (ну и автор) прям натолкнули на мысль, а есть ли геометрические объекты, соответствующие парам чисел при больших степенях! (например, a^3 + b^3 = c^3)
Только потом вспомнил, что таких пар нет.
Правда, тройки наверняка есть. Или хотя бы четвёрки. Уж не кроется ли геометрический смысл теоремы Ферма в геометрии высших измерений?
Pshir
14.01.2018 03:54Конечно, можно вводить «расстояния» не квадратичной формой, а с помощью высших степеней. Но из этого, в любом случае, никак не воспоследует наличие или отсутствие целочисленных решений соответствующих уравнений. Так же, как из теоремы Пифагора никак не следует наличие или отсутствие целочисленных решений a^2+b^2=c^3.

lordn
14.01.2018 11:06Теорема Ферма, что для любого натурального числа n>2 уравнение:
a^n+b^n=c^n
не имеет решений в целых ненулевых числах a,b,c.судя по всему у этой теоремы д.б. расширение типа
x(1)^n+x(2)^n+...x(m)^n = X^n
где m — метрика пространства
с тем же самым ограничением для n>2
видимо это д.б. как-то связано с каким-то из фундаментальных свойств m-мерного пространства.
связь безусловно есть. по-крайней мере теорема ферма утверждает, что в двумерном пространстве нет возможности создать еще одну теорему Пифагора с каким-то иным доказательством и свойствами.
возможно это свойство пифагоричности пространства?
: о)

engine9
13.01.2018 19:12+1этот момент был самым ярким и самым запоминающимся. Я испытал полную гамму чувств, эмоций, переживаний первооткрывателя
Вот это классное ощущение и есть доказательство того, что наука и самообразование могут приносить физическое удовольствие. Помню подобный эпизод из школы. Когда нам учительница предложила пари: мы решаем задачу «из университета» и она нам ставит пятерку за верный ответ. Причем пятерка была, с ее слов, приравнена к оценке за контрольную.
Класс на эти пару дней преобразился, мало кто бегал на перемене, почти все думали над задачей. Даже те, кто не очень любил геометрию или был «двоечником».
Ко мне решение пришло утром, почти во сне, записал его и бегом побежал в школу. М — мотивация. Занятно, что решений было несколько, на уроке мы их разобрали и это был хороший опыт. Жаль единичный.

Krapiv
13.01.2018 19:12Но у вас неправильная формулировка.
- На рисунке пирамида трехгранная.
(Египетские пирамиды четырехгранные) - Не один из углов должен быть прямой, а именно верхний — для пирамиды "на боку" как на рисунке, теорема не выполняется.
Возьму на себя смелость альтернативной формулировки: "у трехгранной пирамиды, у которой в одной из вершин грани сходятся под прямым углом, сумма квадратов площадей этих граней равна квадрату площади оставшейся грани"

938MeV Автор
13.01.2018 19:16+1Там все верно. Просто не хотел перегружать чертеж значками прямых углов. В тексте все написано. Вершина пирамиды лежит в начале координат. Боковые ребра пирамиды располагаются вдоль координатных осей. Трехгранные пирамиды — это сленг так как у минимальной пирамиды 4 грани. Я решил придерживаться официальной терминологии. Поэтому называл пирамиды четырехгранными.

Krapiv
13.01.2018 20:35Да, согласен, перечитал, ваше верна. За исключением того, что не указано, что "боковые" — считаются те, что прилегают к прямому углу. А это не очевидно. И по чертежу тоже.
- На рисунке пирамида трехгранная.

dyakov
13.01.2018 21:49Отличная статья!
Теорема Пифагора, конечно, легко доказывается, но то, что в a, b, c можно подставить натуральные числа теорема же не доказывает. Для меня до сих пор остается загадкой почему существуют такие тройки и почему их так много (начиная с самых малых). Если бы такие тройки существовали из каких-то огромных чисел типа 7978^2 + 24791874^2 = 7226746^2, то это было бы не удивительно, поскольку можно было бы сослаться на совпадение. Даже не было бы удивительным, если бы не существовало бы ни одного набора натуральных чисел, для которых a^2 + b^2 = c^2
Может кто-нибудь знает теорему по этому вопросу?
galaxy
14.01.2018 00:38Любая примитивная пифагорова тройка (x,y,z), где x — нечётно, а y — чётно, однозначно представляется в виде (m^2-n^2, 2mn, m^2+n^2) для некоторых натуральных взаимно простых чисел m>n разной чётности.
Примитивные пифагоровы тройки

DmitriyN
14.01.2018 00:38Вот здесь очень хорошая визуализация https://www.youtube.com/watch?v=QJYmyhnaaek.

Keyten
14.01.2018 01:24Ну вот смотрите, есть тройка (3, 4, 5). Давайте возьмём этот треугольник и пропорционально увеличим в 2 раза. А углы-то те же. И оп! — новая тройка (6, 8, 10).
Давайте увеличим в n раз — а вот и троечка (3n, 4n, 5n). Таким образом, таких треугольников как минимум столько же, сколько и действительных чисел.
Moonrise
14.01.2018 07:28Поправка: треугольников столько же, сколько натуральных чисел. Действительных всё же побольше.

Keyten
15.01.2018 22:15А у вас треугольники только с натуральными сторонами есть?)
А вот смотрите, например, (3pi, 4pi, 5pi):
(3pi)^2 + (4pi)^2 = 9pi^2 + 16pi^2 = 25pi^2 = (5pi)^2
Про континуум знаю. Но я-то рассматриваю треугольники в mathbb R^2.

MStrechen
14.01.2018 16:05Скорее натуральных, мощность NxNxN такая же, что и N, а пифагоровы тройки являются подмножеством этого множества :)

Keyten
15.01.2018 22:15А у вас треугольники только с натуральными сторонами есть?)
А вот смотрите, например, (3pi, 4pi, 5pi):
(3pi)^2 + (4pi)^2 = 9pi^2 + 16pi^2 = 25pi^2 = (5pi)^2
Про континуум знаю. Но я-то рассматриваю треугольники в mathbb R^2.

vitaliy2
14.01.2018 09:58Допустим, у Вас есть 1 монета 10 рублей, одна 5 рублей и одна 1 рубль. Какова вероятность, что Вы сможете набрать 15 рублей? А 16? А 17? В первых двух случаях Вы сможете набрать, а в третьем нет. Тут нет чего-то удивительного.
С квадратами также. Допустим, Вы собираете a? + b? + c? = d? и хотите собрать 81 из ровно 3 чисел. Но чисел на выбор у Вас достаточно много: это и 1, и 4, и 9, и 16, и 25, и 36, и 49, и 64. Суммарно 8 чисел. Из них можно собрать:
14, 21, 26, 29, 30, 35, 38, 41, 42, 45, 46, 49, 50, 53, 54, 56, 59, 61, 62, 65, 66, 69, 70, 74, 75, 77, 78, 81, 83, 84, 86, 89, 90, 93, 94, 98, 101, 104, 105, 109, 110, 114, 116, 117, 122, 125, 129, 138, 149 — суммарно 49 чисел. Т.?е. из 150 чисел мы можем собрать треть, поэтому такие «совпадения» неудивительны. Если выйти за пределы восьмёрки, то из 150 чисел соберётся 70 — это почти половина.
Из комбинаций двух квадратов тоже можно собрать много чисел:
5, 10, 13, 17, 20, 25, 26, 29, 34, 37, 40, 41, 45, 50, 52, 53, 58, 61, 65, 68, 73, 74, 80, 82, 85, 89, 90, 97, 100, 101, 104, 106, 109, 113, 116, 117, 122, 125, 130, 136, 137, 145, 146, 148, 149, 153, 157, 160, 164, 169, 170, 173, 178, 180, 181, 185, 193, 194, 197, 200 и т.?д.
Если собирать a? + b?, то:
Из 1000 первых чисел собираются 293 числа (29%). Среди них собираются 11 квадратов из 31 (35%).
Из 10000 чисел — 2649 (26%). 52 квадрата из 100 (52%).
Из 100 тыс чисел — 23760 (24%). 220 квадратов из 316 (70%).
Из 1 млн чисел — 215594 (22%). 881 квадрат из 1000 (88%).
Если собирать a? + b? + c?, то:
Из 1000 первых чисел собираются 728 чисел (73%). Среди них собираются 19 квадратов из 31 (61%).
Из 10000 чисел — 8166 (82%). 82 квадрата из 100 (82%).
Из 100 тыс чисел — 83102 (83%). 294 квадрата из 316 (93%).
Из 1 млн чисел — 833039 (83%). 973 квадрата из 1000 (97%).
vitaliy2
14.01.2018 15:34Упс, это всё было для случая, когда длины сторон должны быть разными. Исправляю коммент (а заодно и ошибку в вычислении a? + b?):
[…]
С квадратами также. Допустим, Вы собираете a? + b? + c? = d? и хотите собрать 81 ровно из 3 чисел. Но чисел на выбор у Вас достаточно много: это и 1, и 4, и 9, и 16, и 25, и 36, и 49, и 64. Суммарно 8 чисел. Из них можно собрать:
3, 6, 9, 11, 12, 14, 17, 18, 19, 21, 22, 24, 26, 27, 29, 30, 33, 34, 35, 36, 38, 41, 42, 43, 44, 45, 46, 48, 49, 50, 51, 53, 54, 56, 57, 59, 61, 62, 65, 66, 67, 68, 69, 70, 72, 73, 74, 75, 76, 77, 78, 81, 82, 83, 84, 86, 88, 89, 90, 93, 94, 96, 97, 98, 99, 101, 102, 104, 105, 107, 108, 109, 110, 114, 116, 117, 121, 122, 123, 125, 129, 132, 134, 136, 137, 138, 144, 147, 149 — суммарно 89 чисел. Т.???е. из 150 чисел мы можем собрать больше половины, поэтому такие «совпадения» неудивительны. Если выйти за пределы восьмёрки, то из 150 чисел соберётся 105 — это 70%.
Из комбинаций двух квадратов тоже можно собрать много чисел:
2, 5, 8, 10, 13, 17, 18, 20, 25, 26, 29, 32, 34, 37, 40, 41, 45, 50, 52, 53, 58, 61, 65, 68, 72, 73, 74, 80, 82, 85, 89, 90, 97, 98, 100, 101, 104, 106, 109, 113, 116, 117, 122, 125, 128, 130, 136, 137, 145, 146, 148, 149, 153, 157, 160, 162, 164, 169, 170, 173, 178, 180, 181, 185, 193, 194, 197, 200 и т.???д.
Если собирать a? + b?, то:
Из 1000 первых чисел собираются 309 чисел (31%). Среди них собираются 10 квадратов из 31 (32%).
Из 10000 чисел — 2691 (27%). 42 квадрата из 100 (42%).
Из 100 тыс чисел — 23874 (24%). 162 квадрата из 316 (51%).
Из 1 млн чисел — 215908 (22%). 567 квадратов из 1000 (57%).
Если собирать a? + b? + c?, то:
Из 1000 первых чисел собираются 800 чисел (80%). Среди них собираются 23 квадрата из 31 (74%).
Из 10000 чисел — 8283 (83%). 88 квадратов из 100 (88%).
Из 100 тыс чисел — 83268 (83%). 301 квадрат из 316 (95%).
Из 1 млн чисел — 833251 (83%). 982 квадрата из 1000 (98%).

northzen
14.01.2018 10:20Про генерацию пифагоровых троек:
ru.wikipedia.org/wiki/%D0%9F%D0%B8%D1%84%D0%B0%D0%B3%D0%BE%D1%80%D0%BE%D0%B2%D0%B0_%D1%82%D1%80%D0%BE%D0%B9%D0%BA%D0%B0#%D0%93%D0%B5%D0%BD%D0%B5%D1%80%D0%B0%D1%86%D0%B8%D1%8F_%D1%82%D1%80%D0%BE%D0%B5%D0%BA
paluke
14.01.2018 10:43+2А чего тройки то? Четверки же: https://ru.wikipedia.org/wiki/Пифагорова_четвёрка
Про целочисленный прямоугольный параллелепипед есть нерешенная проблема: https://ru.wikipedia.org/wiki/Совершенный_кубоид

Kiano
13.01.2018 23:21Примерно похожее чувство я испытал в школе, в классе 7-ом, когда, как мне тогда казалось, я открыл "свойство" (или формулу) нахождения диагонали у куба. Просто одну сторону умножить на корень из 3. И совсем скоро я расстроился, многие об этом давно знали.
Спасибо, автор, разделяю Ваши чувства и ощущения ;-)
Keyten
14.01.2018 01:26Это следствие из теоремы Пифагора :)
Я тоже что-то открывал, но уже не помню, что. Потом оказалось, что это очень простое следствие из свойств умножения и сложения.

938MeV Автор
14.01.2018 10:01У меня товарищ по универу много физических эффектов предсказал. Правда потом мы их на лекциях проходили через пару недель. Например, он догадался, что должен существовать эффект Холла.

Kiano
14.01.2018 11:36а путь мысли он озвучивал? Если помните — напишите, это порой интереснее результата!)

vitaliy2
14.01.2018 15:40Диагональ прямоугольного многогранника находится абсолютно по той же формуле, что и формула в статье: корень из (a? + b? + c?). Аналогично для объекта любой размерности — это легко вычисляется по стандартной теореме Пифигора. Вначале я даже было подумал, что статья будет об этом.

myxo
14.01.2018 00:04Спасибо, хорошая история для вечера субботы =)
PS. ru.wikipedia.org/wiki/Равенство_Парсеваля

2creker
14.01.2018 00:05Вы ещё молоды, можно понять. Я в университете в дипломной работе придумал по сути новый способ доказательства для определенного класса задач. Так и написал в дипломной — новый способ… Научный (к слову гениальный учёный), который и предложил идею, посоветовал быть поскромнее. Фразу эту убрал .) У нас не особо принято хвастаться в науч. сфере, я так понял что хорошим тоном считается, когда вашу работу хорошо приняли другие учёные.

938MeV Автор
14.01.2018 10:05Это ведь не научная работа, а популярная статья. Я согласен, что теорема простая и ничего особенного тут нет. И теорему я не присваивал. В статье все написано. Прочитайте. Если не принято хвастаться, то зачем же вы сами сейчас хвастаетесь, уважаемый ученый?

2creker
14.01.2018 14:25Ну у Вас написано — Новая теорема Пифагора. Я не хвастаюсь, мне все равно. Я просто понял, что надо быть скромнее в заявлениях.

938MeV Автор
14.01.2018 15:11Согласен, может быть, не совсем корректно. Все же оставил именно такое название для интриги, так как «Обобщенная теорема Пифагора» как-то звучит, на мой вкус, недостаточно интересно. Если бы это была научная работа, было бы скромнее.

Pshir
14.01.2018 00:45Вот странно. Вы же ВУЗ по физмат специальности заканчивали? Описанное в посте — это упрощённый частный случай связи между поверхностными интегралами первого и второго рода, а это с незапамятных времён проходится на втором курсе матана.

938MeV Автор
14.01.2018 10:07Честно говоря, не понимаю что вы имеете ввиду
упрощённый частный случай связи между поверхностными интегралами первого и второго рода
Можете пояснить более подробно?

KvanTTT
14.01.2018 01:34В жизни, все оказалось гораздо проще и прозаичнее. Я опоздал… Но на сколько! Всего-то навсего 18 лет! Под страшными продолжительными пытками и не с первого раза Гугл признался мне, что эта теорема была опубликована в 1996 году!
Слишком простая теорема — было бы странно, если бы ее только в 1996 году доказали. У меня в школе тоже были подобные "теоремы", хорошо что почти никому о них не рассказывал — сейчас стыдился бы.

938MeV Автор
14.01.2018 10:10Что ж, таков мой уровень интеллекта. Думаю, здесь ничего стыдного нет. Признаюсь, что на более серьезную математику у меня возникает гораздо меньше идей.

Ultratech
14.01.2018 10:08+1Очень круто…
Но на первом курсе матана была формула для сферы в трехмерных координатах
x^2+y^2+z^2=R^2, где R — радиус сферы.
Аналогичным образом ищется большая диагональ параллелепипеда.
Давайте проблематику поднимем на более высокий уровень, и совершим несложное открытие:
Представим, что R — это число Грэмма, насколько многомерным должно быть пространство, чтобы выполнялось приведенное выше выражение?
dezdichado
15.01.2018 12:36Чтобы выполнялось приведённое выше равенство, достаточно одномерного пространства с x, равным числу Грэма)

viteralex
14.01.2018 10:10+1С этой пирамидой, у которой при одной вершине угол прямой, был курьёз на подготовительных курсах в университет. Уже более 20 лет назад. Задача была в том, чтобы найти объём, зная длину ребра при прямом угле. Все три ребра одинаковы. Решение оказалось банальным, но никто из абитуриентов его не нашёл. До сих пор помню как пример нестандартного мышления

legrus
14.01.2018 10:58А чего нестандартного? У любой пирамиды объем разве не треть площади основания на высоту?

viteralex
15.01.2018 00:07А нестандартного то, что этот самый прямой угол находился вверху и чтобы понять, что одно из его ребёр является высотой, нужно пирамиду перевернуть на боковую грань. До этого мы, 17-летние абитуриенты, не додумались.

legrus
15.01.2018 12:47А, понял, никто не заметил именно «простого решения», при этом возможно решив «в лоб». Если не подумать о перевороте, придётся применить пяток теорем Пифагора, а то и косинусов.

vlad230596
14.01.2018 10:11+1Мне эта теорема была известна как Фаульхабера. Я в школе в рамках научной работы обобщал её для случая произвольного тетраэдра(когда имеем произвольные, а не прямые углы напротив основания). По сути, это был трёхмерный аналог теоремы косинусов, которая при ? = 90° вырождается в теорему Пифагора.

MikailBag
14.01.2018 11:37геометрическое доказательство того, что можно раскрывать скобки?

vlad230596
14.01.2018 12:39У меня получилась вот такая формула:

Чтобы её получить, я использовал теорему косинусов, формулу Герона, тригонометрические тождества и, да, много раз раскрывал скобки.

lordn
14.01.2018 10:12прикольно, а я только сейчас увидел в геометрическом доказательстве т.Пифагора доказательство выражения
(a+b)(a+b)=a^2+2ab+b^2
кто-нить раньше его уже видел?
: о)

9th-Remin
14.01.2018 10:13+1Автору респект!
Однако, в вашей интерпретации остаётся совершенно не понятно почему бывают целочисленные четвёрки? Сколько их? И можно ли их как-то описать?
В случае египетских треугольников на все эти вопросы можно дать изящный ответ:
1) Прежде всего переформулируем задачу: мы ищем целые числа a,b,c, т.ч
(a/c)^2+(b/c)^2=1
Иными словами мы ищем рациональные числа x=a/c, y=b/c, т.ч x^2+y^2=1
2) Такие числа — это просто точки на единичной окружности с рациональными координатами
3) Последнее наблюдение (имеющее геометрическую интерпретацию) состоит в том что на окружности можно ввести «рациональную параметризацию»
x=(t^2-1)/(t^2+1), y=(-2t)/(t^2+1), легко проверить что x^2+y^2=1
4) Теперь ясно что любое рациональное число t даёт вам египетский треугольник, более того не сложно доказать что таким способом получаются все египетские треугольники.
Это доказательсто из книжки В.И.Арнольда «геометрия комплексных чисел, кватернионов и спинов», возможно вам, как любопытному человеку она будет интересна.
Соответственно вопрос, можно ли что-то подобное сделать для «египетских четверок», и может ли в этой задаче помочь ваша геометрическая идея.
Эта задача может оказаться весьма нетривиальной и (если помечтать ) связанной и с алгебраической геометрией и с Ферма.
Удачи!
Deosis
15.01.2018 11:11Для четверок делается точно также, только на сфере.
x = (2t)(2u) / ((t^2 + 1)(u^2 + 1))
y = (t^2 — 1)(2u) / ((t^2 + 1)(u^2 + 1))
z = (u^2 — 1) / (u^2 + 1)

ver-sta
14.01.2018 10:13Для полноты изложения хорошо бы привести значения $a,b,c$ (длины векторов, образующих пирамиду) дающие какой-нибудь набор из «загадочных четверок». Возможен ли случай натуральных $a,b,c$?

Favorite101
14.01.2018 10:13Исключительно изобретательное доказательство теоремы Пифагора!
Храм Науки и Техники в Северной Корее
vk.com/album-36928352_248393172
Pand5461
14.01.2018 11:01Наглядная демонстрация, а не доказательство.
Чтобы понятна была разница — квадрат 8?8 можно разрезать на кусочки и сложить из них прямоугольник 5?13. Но это не доказательство, что 8?8 = 5?13.


longcake
14.01.2018 11:22Нет, так сделать нельзя, тут треугольки на первой картинке и четырехугольки на второй имеют разную площадь. У треугольников она 12, а у четырехугольков 12,5.

Pand5461
14.01.2018 11:56Я, по-вашему,
зелёный от оранжевого64 от 65 отличить не могу? Конечно, идеально математически не сложатся, останутся щели. Но не очень большие, если резать из бумаги — так вообще можно лист слегка растянуть, и будет незаметно.
Речь о том, что физическая демонстрация не может доказать математическое утверждение, может только навести на мысль.
vitaliy2
14.01.2018 17:45В примере из статьи мы ничего не вычисляли. Горизонтальный размер b получен из исходного определения большого квадрата. Этот рисунок без проблем можно преобразовать в математические формулы и получить то же самое. Просто рисунок читается быстрее, чем скучные формулы.

Pand5461
14.01.2018 18:26+1Вы посмотрите, на что я отвечал исходно.
К рисункам в статье ноль претензий. Я про то, что правильно называть не доказательством, а демонстрацией:


vitaliy2
14.01.2018 22:52Нет, это не демонстрация, а именно доказательство. Там всё обозначается буквами и обозначениями, поэтому даже если Вы что-то искривите или отмасштабируете, ничего не изменится.
Мы берём квадрат стороной (a + b) — его площадь (a + b)?. Площадь внутренних треугольников — a * b / 2. Треугольников 4 штуки. Значит площадь оставшейся части ровно (a + b)? – (a * b / 2) * 4 ?=? a? + 2ab + b? + 2ab ?=? a? + b?. Здесь нет никаких «но» — площадь ровно a? + b?, причём нам даже не понадобилась вторая картинка.
Но нельзя сказать, что вторая картинка тоже не доказывает — все преобразования, которые были сделаны, строго математические. Например, когда известно, что у нас есть два одинаковых прямоугольных треугольника, то точно известно, что из них можно составить прямоугольник с такими же сторонами, причём когда одна сторона этого прямоугольника равна a, и прямоугольник вложен в квадрат со стороной (a + b), то оставшаяся часть справа — это b. Если высота прямоугольника b, то площадь оставшейся части справа будет равно b (которое мы получили ранее), умноженное на b, что равно b?. Именно это и показано на картинке.
Далее раз высота b, а прямоугольник вписан в квадрат стороной (a + b), то оставшаяся высота сверху — a (а ширина a + b). Когда мы убираем такой же прямоугольник с любой из сторон, останется ширина a. Площадь такой оставшейся части будет равна a? (что также показано на картинке). Суммарная площадь оставшихся частей — a? + b? (что и в итоге доказано картинкой).
В Вашем же примере всё наоборот. Во-первых, если чуть поменять форму или размеры фигур, то Ваш пример тут же сваливается (что и происходит). А вот визуальную форму во второй картинке в статье можно менять сколько угодно, т.?к. объекты всё-равно описаны математически, и результат a? + b? от этого не изменится. Во-вторых, Вы не только переместили фигуры, но и изменили их форму.
Pand5461
14.01.2018 23:37Блин, на фотографии с переливающейся жидкостью — демонстрация. В статье доказательство, конечно.
Welran
15.01.2018 07:04Плохой пример. Неправильное геометрическое доказательство сравниваете с физическим.
Zenitchik
15.01.2018 15:43Физическое «доказательство» не надёжнее геометрического. Может вкрасться малая ошибка, незаметная при принятом способе измерения.
Геометрическое «доказательство» показывает пример ошибки, невидимой на глаз, но обнаружимой математически.Welran
17.01.2018 18:42Я и говорю сравнивает ненадежное физическое доказательство с геометрическим вообще не доказательством. Геометрические доказательства надежны и ничем не хуже арифметических. А приведенный пример вообще не доказательство, так как содержит ошибку. Всё равно что написать 2+2=2-0.5+2+0.5=2+0.5+2+0.5= 5 и сказать что это доказательство.
Zenitchik
17.01.2018 19:04Вы, видимо, не уловили мысль. То, что Вы называете «физическим доказательством» — на самом деле тоже демонстрация, которая не доказывает утверждение, а подтверждает его с некоторой вероятностью.

Favorite101
15.01.2018 00:42Квадрат 8?8
можнонельзя разрезать на кусочки и сложить из них прямоугольник 5?13. Останется щель площадью 1 кв. мера вдоль кажущейся прямой диагонали прямоугольника. Эта щель дает прирост площади от 64 кв. мер до 65 кв. мер. Точное описание парадокса здесь.
А в указанном примере с перетекающей жидкостью сумма площадей квадратов, построенных на катетах, точно соответствует квадрату, построенному на гипотенузе — жидкость либо несжимаема, либо в ней нет разрывов.
Pand5461
15.01.2018 01:04В принципе, открытых щелей в углах всех квадратов уже достаточно, чтобы они были не квадратами в математическом смысле. А уже там щели дают 1/65 площади или одну стотысячную — с точки зрения чистой математики не важно.
А так — хорошая, годная демонстрация. Понять её для многих проще, чем математическое доказательство. Но доказательством её это не делает.

blastum
14.01.2018 17:08+1Автору респект и уважуха. Лет двадцать назад тоже до данного решения (алгебраического) додумался. Но претендовать на премию Филдса не стал. Премия Филдса — аналог Нобелевской премии, только для математиков. Правда, возлагал надежды на другую свою разработку: формулу-определение для производных дробного порядка. Когда рассказывал про эти производные, то почти все однокурсники по университету смеялись: это как же получается — дробная производная от константы не равна нулю?
Однажды, один преподователь института посоветовал порыться в математической энциклопедии. И, горе мне! Нашёл в ней некоего немца (фамилию забыл), который это придумал раньше меня лет на 300! Правда, формула-определение у него была другая — мне совершенно не понятная: через интеграл с кружочком. Вот такие дела.
KvanTTT
17.01.2018 17:51Когда рассказывал про эти производные, то почти все однокурсники по университету смеялись: это как же получается — дробная производная от константы не равна нулю?
Тоже о таком задумывался, однако через некоторое время нашел материал по таким производным.
Нашёл в ней некоего немца (фамилию забыл), который это придумал раньше меня лет на 300! Правда, формула-определение у него была другая — мне совершенно не понятная: через интеграл с кружочком.
Вот статья в википедии, которая описывает и производные и интегралы и другие вещи дробного порядка: https://en.wikipedia.org/wiki/Fractional_calculus
Правда, возлагал надежды на другую свою разработку: формулу-определение для производных дробного порядка.
Вычисляется с использованием гамма-функции: Fractional derivative of a basic power function.

blastum
14.01.2018 18:01Если Вы спрашиваете об определении производных дробного порядка, то выдать вот так сразу не могу. Не потому, что я жадный, а потому что подзабыл. Помню, что можно было вычислить сразу производную третьего порядка, например. Правда, от простой функции — степенной. В общих чертах, примерно, так: предел, дробь, в числителе — конечный полином с биномиальными коэффициентами. Для дробных порядков нужно воспользоваться бесконечным рядом, который получается из формулы бинома Ньютона с дробным показателем. Вместо биномиальных коэффициентов я использовал дроби из Гамма-функций.
Если кому то будет интересно, то за недели две смогу восстановить формульно и с примерами.
KvanTTT
17.01.2018 17:57Если так подумать, то в такой формуле ничего сложного нет, т.к. N-ная производная для полиномиальной функции выражается через факториал. А факториал — частный случай Гамма-функции.

censor2005
14.01.2018 22:57Нам в школе в 5 классе преподавательница математики дала задание решить задачу. Для ее решения необходимо было составить уравнение, а уравнения мы к тому времени не проходили. И вот, когда отец объяснил мне суть уравнений, что-то во мне щелкнуло — считаю, что благодаря этому моменту я в будущем стал программистом )
Рад за вас, желаю дальнейших открытий и озарений!

Sirion
15.01.2018 01:22В опросе маловато вариантов. Я, допустим, эту теорему впервые увидел классе в пятом или в шестом, в толстенной энциклопедии для детей, которую мне подарили за победу в олимпиаде. Ни в школьной, ни в университетской программе её не встречал.

dkukushkin
15.01.2018 05:02В школе прочитал про египетский треугольник, что:
3^2+4^2=5^2
Увидел что для степени 3:
3^3+4^3+5^3=6^3 (это так)
Обрадовался, думал что и для всех степеней это работает. Потом проверил для степени 4 — обломился и понял что просто случайно так совпало для 3, для остальных чисел не работает.
938MeV Автор
15.01.2018 12:48Попробуйте придумать тело с такими свойствами. Кубы — это объемы. Получается, три каких-то объема равны какому-то четвертому. Просто у человеков не хватает воображения, чтобы думать в размерностях больших, чем 3. А вдруг там какой-то еще аналог теоремы Пифагора есть?

LoadRunner
15.01.2018 11:1012+42+82=92
Вот тут меня цепляет не равенство суммы квадратов, а то, что на выходе в квадрат возводится простое число (не во всех случаях, но первый случай сам по себе интересен — 1, 4 и 8 — степень двойки и на выходе получается 34.). Есть что почитать на эту тему?
22+32+62=72
32+42+122=132
42+52+202=212
62+132+182=232
Во 2, 3 и 4 примере — первые два возводимые в квадрат числа являются произведением для третьего, что тоже подозрительно.
В 5 примере такого нет, поскольку второе число — простое. Но если из него вычесть 10, то получим 6*3=18. Но, возможно, я просто на ограниченной выборке ищу какие-то закономерности, которых нет на достаточно большом множестве таких четвёрок.
gerahmurov
15.01.2018 18:2521 — тоже не простое, так что, вероятно, это обманка.
Зато мне сразу бросилось в глаза другое (если посмотреть чуть дальше, чем вы описали):
2^2+3^2+6^2=7^2
3^2+4^2+12^2=13^2
4^2+5^2+20^2=21^2
Т.е. видно, что
n^2 + (n+1)^2 + (n(n+1))^2 = (n(n+1)+1)^2
Сразу же проверил
5^2+6^2+30^2=31^2
15^2+16^2+240^2=241^2
Ура, я первооткрыватель!

gerahmurov
15.01.2018 18:30Это примерно так же весело и бесполезно, как школьное наблюдение, что при умножении однозначного чётного числа на 6 получается двухзначное, последняя цифра которого то самое чётное число.

gerahmurov
15.01.2018 18:42Зато теперь всегда смогу быстро найти четвёрку квадратов для такого равенства.
Вероятно, такие пирамиды даже как-то называются.

science_boy
15.01.2018 20:02Это очень круто! С радостью открытия ничто не сравнится :) А можно вопрос: вы написали, что занимаетесь исследованиями. Чем конкретно и где? У меня сейчас в жизни стоит мучительный вопрос между наукой и программированием, пытаюсь определиться
chersanya
15.01.2018 22:52Странно звучит разделение — наука или программирование. Почти в любой науке программирование полезно, часто практически необходимо. И это далеко не только всякие одноразовые скрипты, достаточно большие проекты тоже встречаются.

science_boy
16.01.2018 10:56Да, думаю над компромиссами в том числе. Но нужно определяться, на что делать упор: либо я занимаюсь наукой (что в данный момент для меня вообще никак с программированием не связано), либо ухожу в чистое программирование. Пока что совмещаю: учусь фронтенду и занимаюсь остальным. Но в сутках 24 часа и меня на всё еле хватает

br0x
17.01.2018 11:34Автору (и читателям) наверняка будет интересно посмотреть парочку захватывающих видео, сразу все станет прозрачно, очевидно и красиво.
www.youtube.com/watch?v=G3BhQx1Y5E0
www.youtube.com/watch?v=pHRr3axkrmw
Главное, не пугаться страшных слов, их совсем немного

KES777
17.01.2018 11:48Так как опрос идёт после вашего упоминания теоремы де Гуа, то не могли бы вы уточнить:
>Знали ли вы эту теорему до прочтения статьи?
под словом «эту» вы имеете ввиду теорему Пифагора или де Гуа?
938MeV Автор
17.01.2018 11:49Когда создавал опрос, не знал что она называется де Гуа. Речь идет, конечно, о де Гуа.

Stepler
17.01.2018 12:07+1Помню в начале девяностых, когда учился в Донецком Университете на физическом факультете, с товарищем поигрались с формулой Паули и пришли к неожиданному результату. Для объяснения решили обратиться к профессору Мамолуй Юлии Александровне. Она нас поздравила с изобретением «велосипеда» (поперечный эффект Доплера) и произнесла обнадёживающие слова: «Не стоит расстраиваться из-за очередного велосипеда, главное, что Вы думаете в нужном направлении!»

bodgo
17.01.2018 15:12Уж простите, но почему то вспомнилось
www.youtube.com/watch?v=_GptmtLIh5A

ЗЫ: а как размещать видео в комментариях?


vassabi
эхх! всего на 16 лет опоздать!
У меня из подобного, по школьной физике до сих пор непосчитанная задачка про «составить формулу в общем виде — сколько нужно затратить работы, чтобы повернуть на 180 градусов вокруг своего центра массы пирамиду, которая погружена своей вершиной в воду до центра масс). Так и храню черновик с чертежами, надо будет скормить какой-нить математике или матлабу :)
Zenitchik
Вокруг какой оси повернуть? Если вокруг вертикальной — то зависит от скорости вращения.
aslan7470
Без воды, очевидно, 0. С водой тоже 0, как видно из неполного условия задачи. Но обосновать немогу (