Если вы родились в 1980—90-е, то, вероятно, слышали об игре «Змейка» (Snake). И под «слышали» я подразумеваю «потратили огромное количество времени, выращивая гигантскую дурацкую змею на маленьком экранчике Nokia 3310».

Что ещё вы помните о телефонах Nokia? Их очень долгую работу от аккумулятора, верно? Как такой «примитивный» телефон позволял своему владельцу часами играть в «Змейку», не опустошая аккумулятор?

Короткий (и неполный) ответ: дело в методике скользящего окна (sliding window).

И хотя нам очень хочется написать полноценную статью о «Змейке», всё же здесь мы ограничимся лишь не такой притягательной, но всё же очень важной методикой скользящего окна. И ответим на вопросы:

• Почему мы и другие программисты считаем эту методику фундаментальным алгоритмом?
• Почему он так часто упоминается на собеседованиях по программированию?
• Как он применялся в «Змейке» и прочих «настоящих» приложениях?
• На какие распространённые вопросы на собеседовании можно ответить (лучше), используя методику скользящего окна?

Неважно, готовитесь ли вы к собеседованию, читаете для развлечения или хотите научиться чему-то новому — продолжайте читать. Можете перепрыгивать в любые разделы.
NB: если вас интересует только «Змейка» (ничего, мы понимаем), пролистайте прямо в конец статьи.

Приступим.
Несмотря на сложность алгоритмического программирования, для решения задач в нём используется лишь небольшой перечень основных принципов. Один из них — методика скользящего окна.

Скользящее окно

Оконная парадигма

Методика скользящего окна берёт своё начало в ещё более общем принципе — выводе информации в виде окон: берётся состояние системы и отображается лишь его часть, она же окно. Это позволяет разделить алгоритм представления в виде окна и алгоритм, применяемый к тому, что мы просматриваем в этом окне, в результате оба алгоритма упрощаются.

Бывают ситуации, когда состояние — это последовательность объектов, например массив или строка. Определи окно — и увидишь подпоследовательность. Теперь внутри неё можно применять любую обработку, как если бы в последовательности отсутствовали другие значения. Ограничение диапазона, который мы должны обработать, уменьшает задачи. Теперь перейдём к свойству скольжения: передвинь окно на одну позицию вправо, и теперь отображается другая подпоследовательность, которую тоже можно обработать.

Здесь всё и начинается. Если вы применяете алгоритм отдельно к каждому окну, то придётся прибегнуть к тактике грубой силы.

Однако прелесть методики скользящего окна в том, что она помогает реструктуризировать алгоритм, чтобы воспользоваться самим процессом скользящего окна. И всё это ради создания лучших, более быстрых алгоритмов.

Можно улучшить скорость выполнения практически любого алгоритма, применяемого к скользящему окну — хотя бы в теории. При сдвиге окна меняются только два элемента. Самый старый отпадает, а в кадре появляется новый.

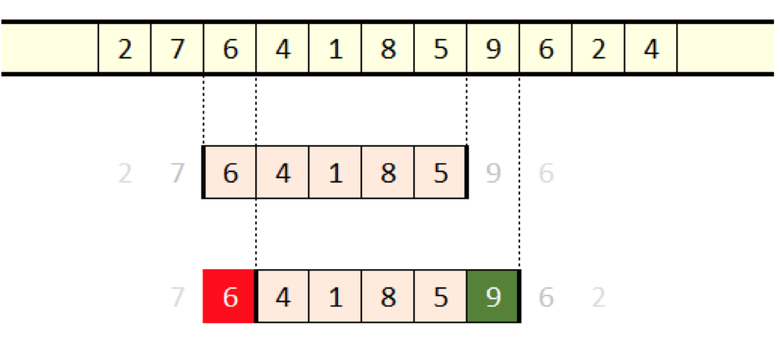
Скользящие элементы (красный отпадает, зелёный появляется)

Если решение в лоб требует k шагов для обработки одного окна длиной k, а в нашей последовательности n окон, то для завершения алгоритма потребуется n*k шагов. Но поскольку при каждом сдвиге окна меняется лишь два элемента, общее выполнение можно снизить примерно пропорционально 2n.

Если мы говорим, что только прохождение последовательности занимает времени O(n), это означает, что на общей последовательности ни один алгоритм не будет работать быстрее O(n). Предыдущий анализ показал, что правильное применение методики скользящего окна может привести к открытию алгоритмов полномасштабной обработки последовательности, которые станут выполняться в течение O(n).

Иными словами, это обещание, что мы можем придумать идеальные алгоритмы, такие, что для решения этой задачи нельзя будет создать ещё более быстрый алгоритм!

Мы закончили с необходимым введением, давайте теперь рассмотрим три программистские задачи, которые можно решить с помощью этой общей алгоритмической концепции, и обсудим реальные примеры её использования.

Задача № 1: скользящее среднее

Задача: создать алгоритм, вычисляющий скользящее среднее для серии чисел.

Для серии a0, a1, … an-1 и параметра k, где 0 < k <= n, нужно сгенерировать новую последовательность, в которой каждый элемент является средним для k последующих элементов исходной последовательности:

Контекст: скользящее среднее полезно для сглаживания потока входных данных. Если на числа влияет шум, то сырые данные может быть трудно читать. Сглаживание помогает строить более информативные графики, как показано ниже.

Скользящее среднее сглаживает входные данные

Эту задачу можно эффективно решить с помощью методики скользящего окна.

Здесь сразу же проявляется характерная особенность большинства подобных алгоритмов: ведущие элементы k-1 не генерируют выходных данных. Первую часть результата можно отправить, только когда целиком заполнено первое окно. Все последующие окна генерируют по одному результату. Следовательно, последовательность из n генерирует последовательность из n-k+1 результатов при обработке алгоритмом скользящего окна.

Теперь о реализации. Среднее окна — это сумма всех элементов, поделённая на длину окна.

Теперь очевидно преимущество использования методики скользящего окна. Сумму окна можно вычислить из суммы непосредственно предшествующего окна:

На вычисление суммы первого окна уйдёт k шагов, для каждого последующего окна — плюс всего лишь по две дополнительные операции.

Ниже показана реализация на С++: программа проходит по ведущим k элементам, чтобы сгенерировать первые выходные данные. Все остальные числа вычисляются с помощью оптимизированной формулы суммирования.

double* moving_average(double* data, int n, int k)
{
   assert(data != NULL);
   assert(n > 0);
   assert(0 < k && k <= n);
   double* result = new double[n — k + 1];
   double sum = 0;
   for (int i = 0; i < k; i++)
   {
      sum += data[i];
   }
   result[0] = sum / k;
   for (int i = k; i < n; i++)
   {
      sum = sum — data[i — k] + data[i];
      result[i — k + 1] = sum / k;
   }
   return result;
}

Главное, что нужно отметить: каждый элемент исходной последовательности обрабатывается максимум дважды, так что общая временная сложность равна O(n).

Задача № 2: подпоследовательность с максимальной суммой

Задача: создать алгоритм поиска последовательности с наибольшей суммой среди всех возможных последовательностей.

Это превращается в настоящую проблему, если входные данные могут содержать отрицательные значения.

Повторимся, что методика скользящего окна может использоваться для нахождения O(n)-решений. Только в этот раз длина окна не будет фиксированной. Это сама по себе непростая задача — найти наиболее подходящую длину окна, она станет меняться по мере работы.

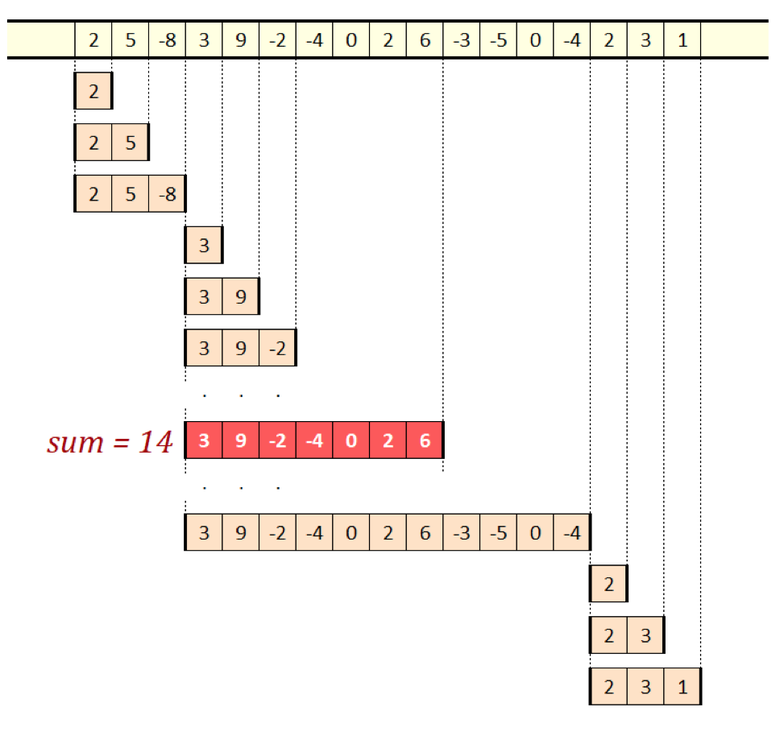
Максимальная сумма скользящего окна

Идея в том, чтобы отслеживать, что происходит, когда у нас уже есть окно с определённой суммой. Затем нужно добавить следующее входящее значение. Оно может быть добавлено к сумме окна, но может быть и взято в качестве совершенно нового окна с длиной в модуль. Теперь принимаем то, у чего сумма больше, за новое окно, перемещаем к следующему входному значению и повторяем процедуру. На иллюстрации выше показано, как окно постепенно скользит по последовательности.

Выигрышный вариант всегда представляет собой подпоследовательность с максимальной суммой, заканчивающуюся текущим входным элементом. Уничтожается каждое окно, чья сумма становится отрицательной: это ситуация, когда лучше оставить одно число, чем объединить его со всем максимальным предшествующим окном.

Остаётся только определить общий максимум. Кандидатом становится каждое окно по мере скольжения к концу последовательности. Когда она заканчивается, подпоследовательностью с высшей суммой будет то окно, чья сумма больше других.

Ниже приведена простая реализация на С++. Повторим, что каждый элемент последовательности оценивается максимум дважды, так что общая временная сложность равна O(n).

std::tuple<int, int, int> max_sum_subsequence(int* data, int n)
{
   assert(data != NULL);
   assert(n > 0);
   int bestStart = 0;
   int bestLength = 1;
   int maxSum = data[0];

   int curStart = bestStart;
   int curLength = bestLength;
   int curSum = maxSum;

   for (int i = 1; i < n; i++)
   {
     if (curSum < 0)
     {
       curStart = i;
       curLength = 1;
       curSum = data[i];
     }
     else
     {
       curLength += 1;
       curSum += data[i];
     }
     if (curSum > maxSum)
     {
       bestStart = curStart;
       bestLength = curLength;
       maxSum = curSum;
     }
   }
   return std::tuple<int, int, int>(bestStart, bestLength, maxSum);
}

Задача № 3: все максимумы из k-подпоследовательностей

Задача: создать алгоритм, вычисляющий максимумы всех подпоследовательностей длиной k в числовой последовательности длиной n. Трудная задача.

Этот алгоритм используется в обработке изображений. В этой сфере, как вы понимаете, алгоритмы с длительностью выполнения O(n) ценятся больше других.

Максимумы

Когда окно сдвигается, оно генерирует максимум, содержащий выходное значение. Трудность решения этой задачи в том, что не существует формулы, вычисляющей максимум для заданного окна. В качестве результата нужно выбрать один из элементов.

Здесь нам тоже может пригодиться методика скользящего окна. Допустим, у нас есть окно с четырьмя значениями, как на картинке выше.

Когда в кадр попадает дополнительное значение, нам нужно понять, как оно соотносится с уже имеющимися. Начнём с того, что по мере скольжения окна все предыдущие значения отпадут до того, как отпадёт новое поступившее. Это важно. Если предыдущее значение меньше нового, значит, оно никогда не будет максимумом.

Смещение

Это наводит на мысль позволить каждому новому значению аннулировать и убирать все меньшие значения, представленные в окне по мере его скольжения, как на картинке ниже. Но у этой операции есть и другое следствие.

Если каждое добавляемое справа значение будет убирать всё, что меньше него, тогда окно станет содержать только не увеличивающуюся и раздробленную подпоследовательность исходного окна. Ещё одно очевидное следствие: крайний левый элемент окна будет максимальным значением, которое мы хотели вычислить.

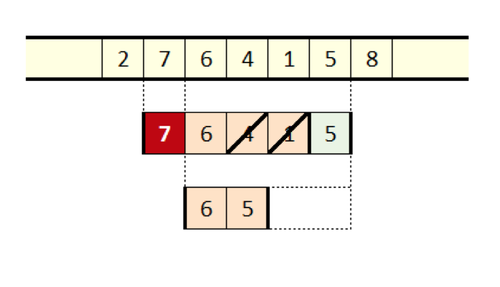
Аннулирование

Нужно прояснить ещё кое-что. По мере скольжения окна крайнее левое значение отбрасывается. Однако оно уже может оказаться отброшенным более крупным значением. А может и пережить всех своих последователей справа. В таком случае входное значение будет крайним левым значением в кадре, и теперь пришла пора его убрать.

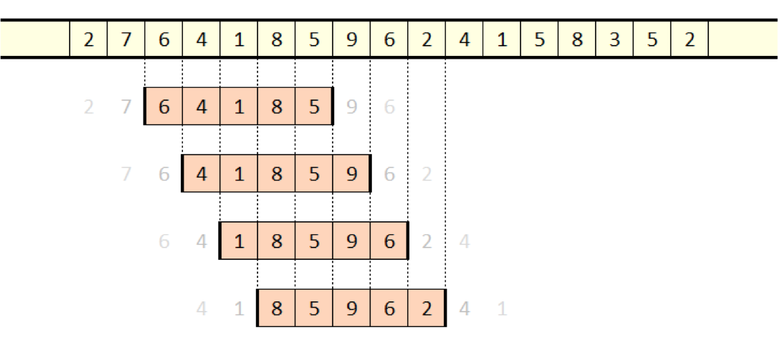
Ниже показан весь процесс, применённый к последовательности из семи элементов, с окном длиной в четыре элемента.

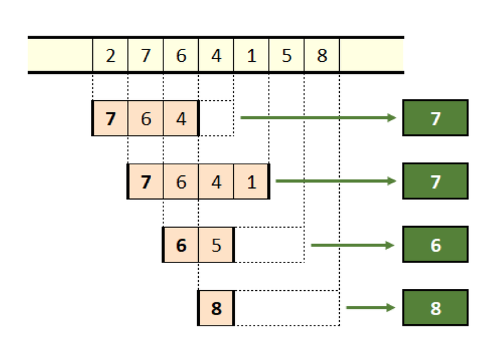
Все максимумы

На этом мы завершаем описание алгоритма и можем его реализовать. Обычно это делается с помощью двусторонней очереди (double-ended queue, dequeue). Она позволяет добавлять и удалять элементы с обоих концов, чем мы и воспользуемся для реализации алгоритма.

void insert_maximum_candidate(int value, bounded_deque<int> &maximums)
{
   while (!maximums.empty() && maximums.back() < value)
           maximums.pop_back();
   maximums.push_back(value);
}
void remove_maximum_candidate(int value, bounded_deque<int> &maximums)
{
   if (!maximums.empty() && maximums.front() == value)
        maximums.pop_front();
}
int* range_maximums(int* data, int n, int k)
{
   assert(data != NULL);
   assert(n > 0);
   assert(0 < k && k <= n);
   bounded_deque<int> maximums(k);
   for (int i = 0; i < k — 1; i++)
        insert_maximum_candidate(data[i], maximums);
   int* result = new int[n — k + 1];
   for (int i = k — 1; i < n; i++)
   {
        insert_maximum_candidate(data[i], maximums);
        result[i — k + 1] = maximums.front();
        remove_maximum_candidate(data[i — k + 1], maximums);
   }
   return result;
}

В этом решении мы используем собственную реализацию двусторонней очереди — fixed_deque. В отличие от std::deque, этот класс поддерживает буфер фиксированного размера для данных, что ускоряет работу как минимум на порядок. Под капотом он работает как кольцевой буфер, что крайне эффективно. Можете скачать реализацию fixed_deque из пакета для этой статьи. В любом случае класс fixed_deque имеет такой же публичный интерфейс, как и у std::deque (разница лишь в том, что его конструктор ожидает получить размер буфера), так что спокойно заменяйте. Всё останется по-прежнему, только выполнение заметно ускорится.

Как и в предыдущих примерах, мы можем проанализировать временную сложность этой реализации. Каждое значение из входной последовательности подаётся в очередь и удаляется из неё только один раз. Получается максимум две операции на каждое входное число, а общая временная сложность алгоритма равна O(n). Также этому алгоритму нужно дополнительное пространство O(k), где k — длина окна. Обратите внимание, что предыдущему алгоритму нужно только O(1).

Мыслим нестандартно

Мы рассмотрели три разных алгоритма на основе методики скользящего окна. Каждый из них исполняется в течение O(n). А сейчас хотим показать вам, как та же методика применяется в двух совершенно разных сферах.

Во-первых, в протоколах маршрутизации запросов, например в TCP/IP, скользящее окно используется для согласования IP с расположенным выше уровнем TCP. IP не гарантирует, что пакеты будут получены в том же порядке, в каком они отправлены. А TCP добавляет эту гарантию. И один из ключевых факторов успеха союза TCP/IP — скользящее окно.

TCP-получатель поддерживает окно пакетов, которые он ожидает. Пакеты прибывают по менее совершенному (но более надёжному) IP, и заполнять окно они могут не в том порядке, в каком нужно. Но как только приходит крайний левый пакет, TCP-окно сдвигается как можно дальше вправо, подтверждает отправителю, что все смежные пакеты получены, и передаёт их на выход. Тот, в свою очередь, командует отправителю слать в IP-сеть последующие пакеты.

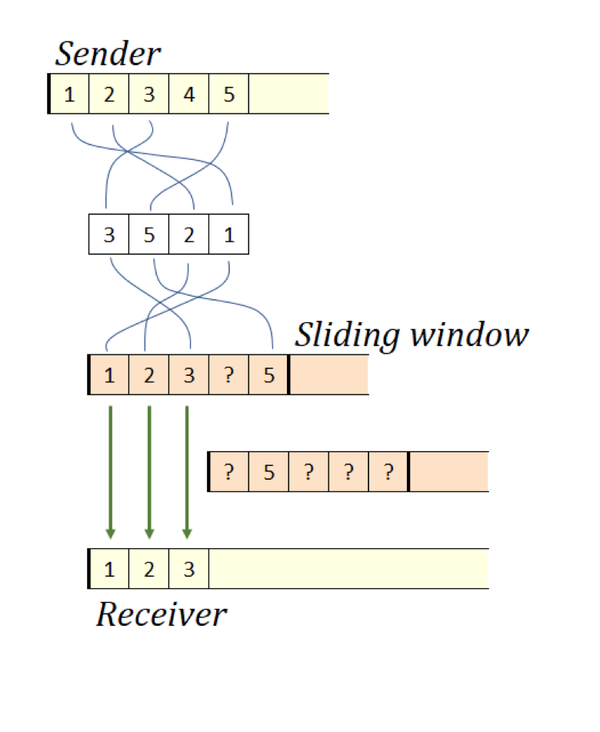
Во-вторых… Вы уже знаете, чем посвящена вторая (и последняя) часть этого раздела.

Она о «Змейке». Поскольку эта игра появилась десятилетия назад, большинство из вас познакомились с ней на телефонах Nokia.

И знаете что? Сама змея — это скользящее окно!

Когда она двигается, на всём экране нам нужно нарисовать только два блока: хвост превращается в фоновый блок, а фоновый блок перед змеёй становится новой головой.

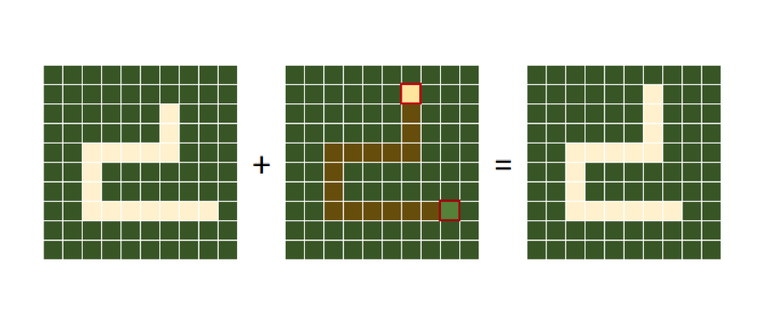
Змея = скользящее окно

В результате каждый такт игры стоит нам всего два простейших блока вне зависимости от длины змеи. Это позволяет реализовать игру на примитивном оборудовании, не нагружая аккумулятор телефона.

Резюме

Мы проанализировали методику под названием «скользящее окно». С её помощью можно оптимизировать алгоритмы обработки последовательностей данных. При успешной реализации методика позволяет создавать алгоритмы, выполняющиеся в течение O(n) для последовательностей из n объектов. Обычно это лучшее, чего можно добиться с учётом структуры алгоритмов.

В качестве конкретных примеров задач мы показали три различных алгоритма, работающих с числовыми последовательностями. У каждого из них своя сфера применения — в реальных приложениях, в общей обработке данных и в обработке изображений. Это объясняет, почему методика скользящего окна до сих пор используется для создания алгоритмов и почему вы наверняка услышите о ней на собеседовании по программированию.