
Давным давно, во времена римской империи, группу еврейских солдат окружила римская армия. Выбор невелик — сдаться или погибнуть. Хитрые евреи придумали систему, чтоб и живыми не сдаваться, и грех самоубийства не совершать. И так до тех пор, пока в живых не останется только один, а уж ему придется покончить с собой. В истории, которую я слышал, герой, Иосиф, хотел спасти себе жизнь и сдаться в плен, а не погибнуть. И поэтому он решил найти заветное место.
(Во время написания поста погибло дофига нарисованных солдатиков).
«Я был в старшей школе, когда профессор Фил сказал мне решить эту задачу.
Он предложил решить ее вручную, на бумаге. Взять разное количество людей и найти закономерность, где n — количество мест, а w(n) место победителя.»
Рассмотрим, что произойдет на примере семи человек: 1 убивает 2. 3 убивает 4, 5 убивает 6. Ну, а для 7 нет 8, поэтому 7 убивает 1. Затем 3 убивает 5, 7 убивает 3. 7 победил.

Это Иосиф, он хочет жить.

У Иосифа в отряде был 41 человек. И вот это уже серьезно.
Рассмотрим пример, когда в группе 5 человек. 1 убивает 2, 3 убивает 4, 5 убивает 1, 3 убивает 5. Победителем становится 3.
Для шестерых. 1 убивает 2, 3 убиваетс4, 5 убивает 6, 1 убивает 3 и 5 убивает 1. Победитель — 5.
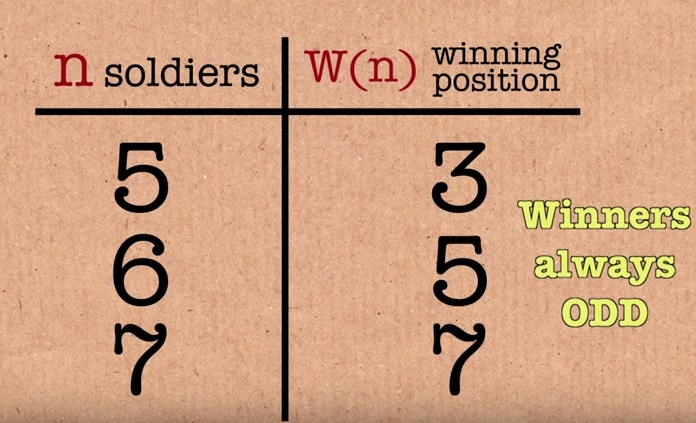
Появляются странные закономерности. Пока что победитель — это нечетное число.
Попал на четное место — кранты.
А теперь полностью заполним таблицу.
Возьмем одного человека. Что ж. Этот человек победил, так что это было легко.
Если есть два человека: 1 убивает 2. 1 — победитель.
Если есть три человека: 1 убивает 2, 3 убивает 1. 3 выиграл.
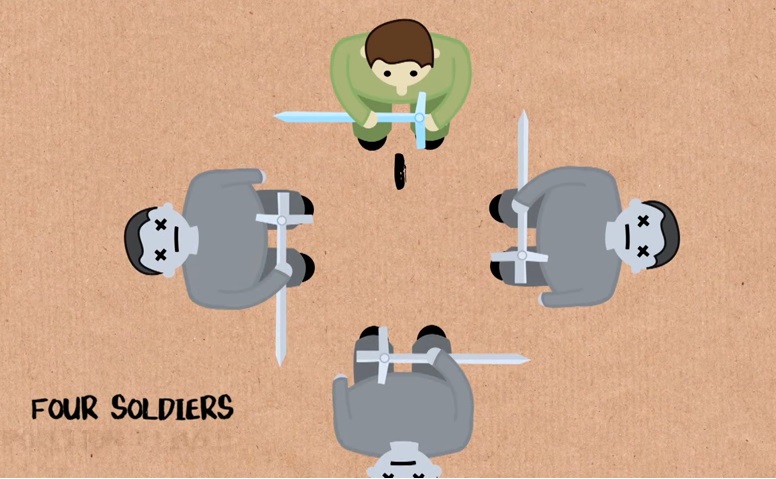
Если есть четыре человека: 1 убивает 2, 3 убивает 4, 1 убивает 3.
Если есть восемь человек: 1 убивает 2, 3 убивает 4, 5 убивает 6, 7 убивает 8, 1 убивает 3, 5 убивает 7, 1 убивает 5. Победителем становится 1.
Хорошо, результаты таковы: 1, 1, 3, 1, 3, 5, 7, 9.
Результат все время увеличивается на 2, но затем он сбрасывается в какой-то момент.
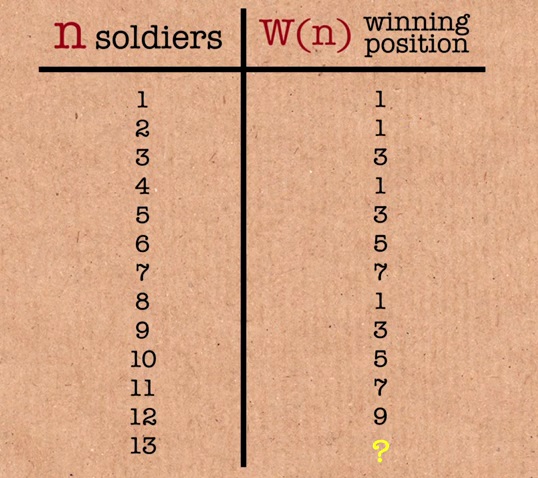
Сделаем быстро к 13, получим 11, а у 14 будет 13.
Теперь посмотрим, когда случится сброс до одного. Обратим внимание на числа, которые дают вам единицу. Уже можно догадаться, что у 16 победителем будет 1.
Сделаем вывод:
Если n (количество человек) — это 2 в степени, то выигрышное место — номер один.
Теперь я нарисую схему побольше. Схема на 16 человек.
После первого круга убийств останется вдвое меньше человек, то есть 8. Теперь опять начнем с первого. Проходимся по кругу, и снова вдвое меньше, то есть 4. Делаем еще один круг. Осталось два человека.Начинаем с номера один, и он побеждает.
А теперь рассмотрим, что происходит с числами, между 4 и 8.
Результат увеличивается на два. Но, когда я к 7 добавляю 2, то получается 9. Вот здесь и случится сброс до 1. И теперь я могу сказать, что, любую комбинацию можно расписать как 2 в степени плюс еще какое-то число.
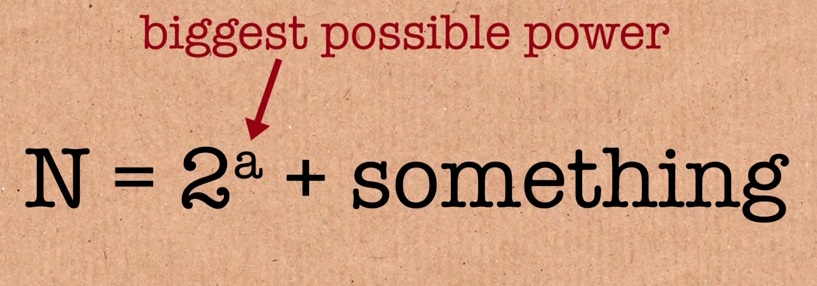
Возьмем число 77. Самая большое число, из которого я могу извлечь корень — это 64. Тогда получим сумму: 64 + 13.
Затем распишем по такой же схеме для числа 13 самые большие корни: 8 + 4 + 1. Получается сумма двоек в степенях. 77=2?+2?+2?+2?. Ключевой момент в том, что степени не повторяются, значит мы все сделали правильно.
А теперь выведем формулу, где 64(n) — это 2 в степени А + 13 — это L, получится n=2?+l
13 мы распишем, как сумму: 8+4+1 и подставим формулу n=2?+l (13=8+5)
И нечетное число является количеством ходов, после которого нужно остановиться.
Я сделаю пять шагов. Итак: 1 убивает 2, 3 убивает 4, 5 убивает 6, 7 убивает 8, 9 убивает 10. Я остановился на номере 11. Теперь смотрите, что происходит: сколько людей осталось? То, что осталось — это и есть корень из двух. И как мы знаем, тот, кто победит в корне из двух — это тот, кто начнет!
Теперь смотрим: 11 убивает 12, 13 убивает 1, 3 убивает 5, 7 убивает 9. Снова возвращаемся к одиннадцатому, теперь осталось всего четыре человека. 11 убивает 13, 3 убивает 7.Осталось 2 человека и одиннадцатый начинает. 11-й победил.
Теория заключается в том, чтобы расписать число по формуле, где L меньше, чем 2 в степени a. А выигрышное место — это 2L+1.
У нас последняя сумма была 13=8+5, где 5 было L. Подставим в формулу и увидим, что все сходится: 2*5+1=11
Вернемся к нашей задаче. Там был 41 человек в отряде. 41=32+9
Возьмем нашу формулу 2L+1. Получим 19
Рисуем круг.
Итак, 1 убивает 2…
Мы теряем наши четные цифры.
41 убивает 1, 3 убивает 5...19 убивает 35, 35 убивает 1 и 19 убивает 35.
Формулу, что я написал, можно расписать в двоичном коде.Напишем сумму степеней: 41=2?+ 2?+2?. Код представляет собой ни что иное как двойки в степени. А код — это единица или ноль. Запишем по порядку двойки в степени слева самая большая в конце два в степени 0. Там, где степень соответствует нашему значению, то ставим 1, в ином случае — 0. Таким образом получаем: 2? 2? 2? 2? 2? 2?. Двоичный код будет: 2? — это 1, 2? — это 0 и т.д… И получаем: 101001.
А сейчас покажу основную фишку в решении задачи. Выигрышная позиция будет вашим двоичным кодом, но первую цифру нужно перенести назад: 010011. Получается: 2?+2?+(я пропустил 2? и 2?)+2?. А вот и сумма: 16+2+1, где ответ 19.
Вот и все решение для нашей задачи.
P.S.
И в этом положении Иосифа не покинуло его благоразумие: в надежде на милость божью он решил рискнуть своей жизнью и сказал: «Раз решено умереть, так давайте предоставим жребию решить, кто кого должен убивать. Тот, на кого падет жребий, умрет от рук ближайшего за ним, и таким образом мы все по очереди примем смерть один от другого и избегнем необходимости сами убивать себя; будет, конечно, несправедливо, если после того, как другие уже умрут, один раздумает и останется в живых». Этим предложением он вновь возвратил себе их доверие; уговорив других, он сам также участвовал с ними в жребии. Каждый, на кого пал жребий, по очереди добровольно дал себя заколоть другому, последовавшему за ним товарищу, так как вскоре за тем должен был умереть также и полководец, а смерть вместе с Иосифом казалась им лучше жизни. По счастливой случайности, а может быть, по божественному предопределению, остался последним именно Иосиф еще с одним. А так как он не хотел ни самому быть убитым по жребию, ни запятнать свои руки кровью соотечественника, то он убедил и последнего сдаться римлянам и сохранить себе жизнь. Иудейская война, книга 3, глава 8, 7
Читать еще
- Josephus Problem на сайте Вольфрама
- Видеолекция профессора Steven Skiena
- Josephus problem на Википедии
О школе GoTo
- Конкурс GoTo Algorithms Challenge Spring 2018 (до 21 марта)
- Весенняя школа GoTo 2018 (25-31 марта)
- Группа в ВК
- Подписаться на рассылку
Комментарии (19)

PapaBubaDiop
13.03.2018 16:33Степени двоек — это прекрасно, но почему бы Иосифу не уговорить всех 41 остаться в живых? Гнусный тип этот Иосиф.
Кстати, есть советский фильм «41-ый», и это про число зарубок на снайперской винтовке девушки. И 41-ый враг тоже оказался роковым, как в Библии…vesper-bot
13.03.2018 18:11+2> почему бы Иосифу не уговорить всех 41 остаться в живых?
Там была демократия, пока было больше за помереть, они и помирали, последний остался уже без большинства, и стало можно его убедить.
PapaBubaDiop
13.03.2018 19:12Демократия — слово греческое, к евреям вообще никак не относится, иначе бы парни не пошли за Моисеем)

dryzhakov
14.03.2018 11:10Иосифу в детстве задачку задали «У тебя шесть яблок, половину отдал брату, сколько у тебя осталось?» «Таки пять с половиной!». Воюй потом с такими :-)
MAXHO
14.03.2018 11:57+1Скорее римская демократия, в лице Веспасиана, пришла в погрязший в теократических суевериях Израиль… Ну и как обычно не оставила камня на камне… Традиция со времен Трои ;)
Вообще история интересная и поучительная. И эта задачка только маленький фрагмент этой войны. Если не ошибаюсь дело происходило в Масаде. И там было очень много народу. В том числе женщины и дети. Все пошли под нож. В 63 годах были найдены глиняные таблички, которые использовались в этом жребии смерти. Так что скорее всего история имела место быть.

StjarnornasFred
15.03.2018 23:51А у меня другой вопрос.
группу еврейских солдат окружила римская армия. Выбор невелик — сдаться или погибнуть.
А воевать не пробовали?
Как говорится, с такими друзьями и враги не нужны.

lieh_tzu
13.03.2018 23:16+1Доказательство: Р.Грэхем, Д.Кнут, О.Паташник, Конекретная математика, стр. 25-33

EndUser
14.03.2018 09:53У Мартина Гарднера, вроде бы, это было.
Ответ давался без доказательства: для выигрышного номера надо взять двоичное представление количества участников и перенести левую единицу направо.
Кажется, популяризатор математики так же упомянул отсутствие толковых исторических доказательств случая.
tyomitch
16.03.2018 01:39А какие могут быть доказательства, если выжил один только Иосиф?
Вот только из его мемуаров об этой истории и известно.

onick7
14.03.2018 11:10+1А так как он не хотел ни самому быть убитым по жребию, ни запятнать свои руки кровью соотечественника, то он убедил и последнего сдаться римлянам и сохранить себе жизнь.
Если они действовали по озвученной логике, то Иосиф уже должен был запятнать руки, прежде чем вдвоем остаться, каким бы он ни стоял. Что-то не сходится…vesper-bot
14.03.2018 12:43+1Из истории — они действовали по жребию, т.е. жребий кидается на позицию в круге, который каждый раз уменьшается. В итоге за N-2 попытки жребий ни разу не попал на самого Иосифа и ни разу — на человека перед ним, так что Иосиф оказался не при делах при каждом убийстве. Шанс на это 2/((N-1)*(N-2)), хотя и невелик, но может выпасть. Логику придумывали уже потом, отвязанным от истории образом.
take
14.03.2018 20:11+1Давным давно, во времена римской империи, группу еврейских солдат окружила римская армия.
Это были 60-70 кажется годы первого века нашей эры при будущем императоре Веспасиане. Римляне не группу окружили, а взяв иудейский город и перебив почти всех защитников, обнаружили спратавшихся за источником воды в пещере нескольких выживших евреев вместе с Иосифом. Римляне стали обещать жизнь Иосифу, который был руководителем обороны города и известным деятелем. Он хотел сдаться, но его сторонники предложили смерть. Тогда-то и возникла идея со жребием и убийством друг друга. Иосиф (единственный выживший) и написавший это позже в своей книге «Иудейские войны» — утверждал, что это было так. Но других свидетелей не было. Может и иначе )
FadeToBlack
15.03.2018 10:00А я вот не хочу ходить по ссылкам. Я хочу читать цельную статью. Я несколько раз прочитал вступление, но не смог понять задачу. Почему Иосифу просто не прикончить их всех, а самому не сдаться в плен? Какие еще дополнительные условия есть у этой задачи? Какие есть ограничения на то, кто кого должен убивать? Почему этого нет в условиях задачи?

FadeToBlack
15.03.2018 10:10Сходил в википедию, прочитав одно предложение, понял задачу. Зачем тогда такая статья? Мне нужно было сначала пролистать до конца, почитать все это, а потом вернуться к статье? Ну уж нет, если пишите — пишите качественно, почитать википедию я и сам умею, без всяких статей. Зачем я пишу это? Да просто это школа программирования! И это обучающая статья. Нельзя допускать такие ошибки, если хочется учить людей. Если мне нужно ходить в википедию и читать что-то — мне не нужна ваша школа.

Taras-proger
16.03.2018 09:31Вот только по легенде он спасся не только сам, но выбрал выигрышное место и для друга. Они остались двумя последними выжившими. Так что у Вас есть решение, но к задаче оно нее подходит.

JuniorNoobie
16.03.2018 15:20+1У меня возник, возможно, глупый вопрос. Если евреи не хотели брать на себя грех самоубийства, то почему просто не выстроились в очередь, где стоящий за спиной человек убивает впередистоящего, начиная с начала очереди? Я что-то не так понял?


vesper-bot
"Два путешествия с компьютером" — там была такая же проблема, только вместо каждого второго вылетал каждый Х-й, где Х задавался в начале, и нужно было найти два выигрышных места. И вот эту проблему посложнее будет свести к аналитическому решению, имхо. Ну или решение такое же, только вместо двух основание у степени Х, а вся арифметика идет по модулю N.