Мы продолжаем цикл квантовых статей. Сегодня углубимся в формулы и поймем, как можно манипулировать кубитами — элементарными вычислительными единицами. Кроме того, рассмотрим принципы цепей и алгоритмов. Подробнее под катом!

Статьи из цикла:

1. Квантовые вычисления и язык Q# для начинающих
2. Введение в квантовые вычисления

Введение

Задача этой статьи — помочь вам быстро познакомиться с основными принципами работы квантовых вентилей и понять, как эти вентили объединяются в цепи, наглядно представляющие квантовые алгоритмы (некоторые из них мы обсудим в последующих публикациях).

Для вашего удобства я опубликую сводную информацию обо всех важнейших вентилях, элементах схем и т. п. из статей этой серии в виде шпаргалки (чтобы вам не пришлось долго искать нужные сведения). В моих будущих статьях она будет называться «Квантовые вычисления: краткая справка».

Основы: квантовые состояния

Начнем с основ — с обозначений некоторых распространенных квантовых состояний, которыми мы будем впоследствии манипулировать:



Все они являются чистыми однокубитными состояниями, поэтому их можно представить в виде точек на сфере Блоха:



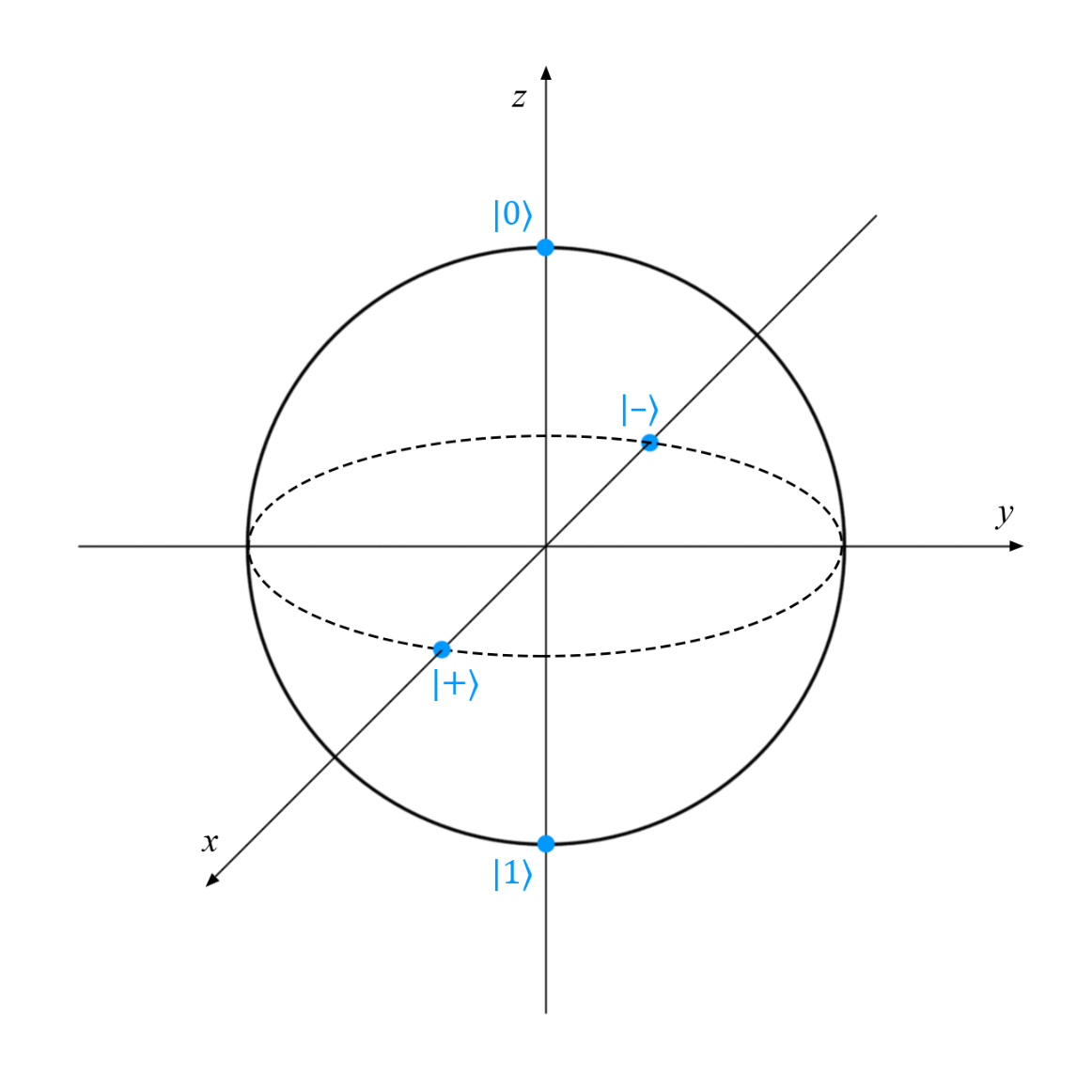
Теперь — четыре состояния Белла (их еще называют парами ЭПР, в честь Эйнштейна, Подольского и Розена — именно они являются авторами идей, которые впоследствии развил Белл). Это простейшие примеры квантовой запутанности двух кубитов:



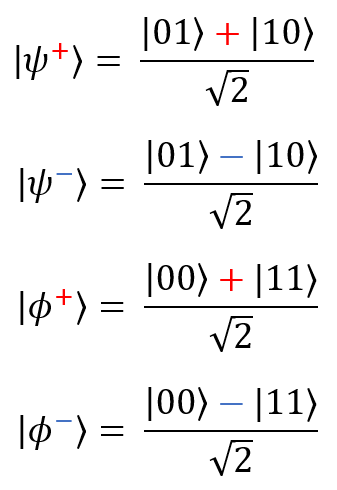
И наконец, мы будем использовать так называемые состояния ГХЦ (Гринберга — Хорна — Цайлингера). Вот их общая форма (для n кубитов) и простейшая форма (для трех кубитов):



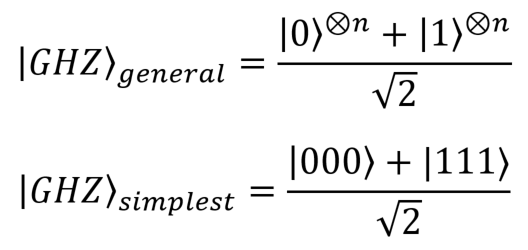
Состояния Белла и состояния ГХЦ очень важны, потому что их поведение кардинально отличается от предсказаний классической теории из-за уровня запутанности в таких системах (этот принцип «максимальной запутанности» будет рассмотрен в одной из последующих публикаций).

Основы: радианы

Углы поворота в теории квантовых вычислений измеряются в радианах. Полная окружность (360°) соответствует 2? радиан. Углы измеряются против часовой стрелки. Ниже показаны величины важнейших углов в градусах и в радианах.

Основы: диаграммы квантовых цепей

Перед тем как углубляться в изучение квантовых вентилей, следует изучить основы построения диаграмм квантовых цепей (это не займет много времени):

• Время на квантовой диаграмме движется слева направо.
• Каждому кубиту соответствует одиночная горизонтальная линия.
• Вентили обычно обозначаются квадратами. Тип вентиля обозначается буквами или другими символами в этом квадрате (бывают и исключения из этого правила. Обычно это кубитные вентили, у которых есть классические аналоги (пример — вентиль NOT)).
• Некоторым вентилям может соответствовать несколько элементов диаграммы (пример — вентиль NOT).
• В результате измерения кубита все суперпозиции коллапсируют, квантовые свойства кубита исчезают, и он превращается в обычный бит. Поэтому можно считать, что измерительный элемент (показанный ниже) принимает на вход кубит и выдает классический бит. Этой операции в языке Q# соответствует команда Measure(bases: Pauli[], qubits: Qubit[]) или M(qubit: Qubit) по основанию Z.

Вот обозначения важнейших элементов:



Более подробная информация приводится в документации здесь и в книге М. Нильсена и И. Чанг «Квантовая информация и квантовые вычисления».

Однокубитные вентили

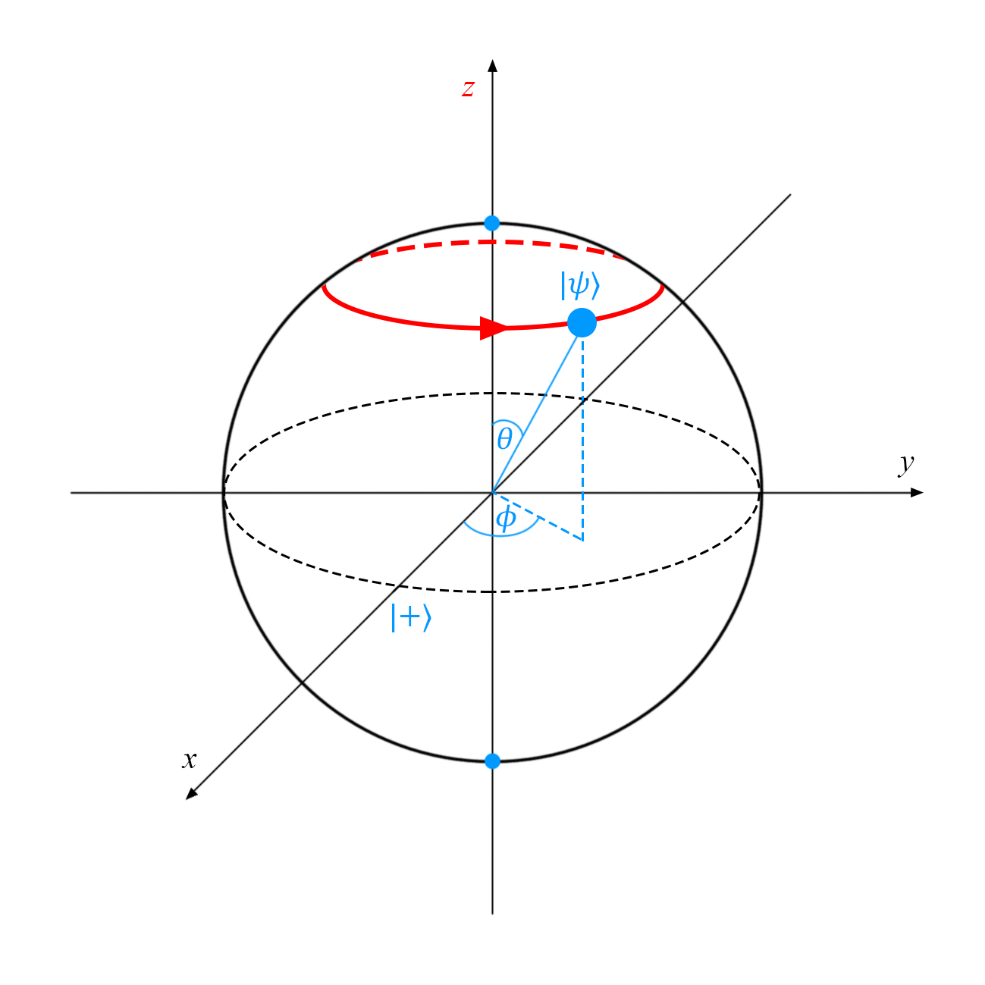
Однокубитные вентили закономерно являются самыми простыми, поэтому мы начнем с них. Операцию, выполняемую любым однокубитным вентилем, можно представить как поворот вектора, характеризующего состояние кубита, в другую точку сферы Блоха (см. ниже).

Самые элементарные однокубитные вентили — это вентили Паули X, Y и Z:

Названия	Матричное представление	Обозначения	Представление в Q#
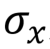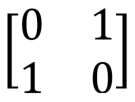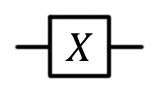Вентиль Паули X, X, NOT, переключение бита,			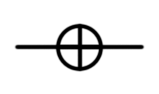X(qubit: Qubit)
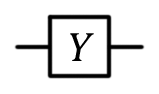
Вентиль Паули Y, Y,	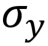		Y(qubit: Qubit)
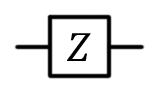
Вентиль Паули Z, Z, переключение фазы,	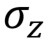		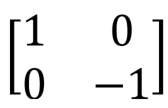Z(qubit: Qubit)

Вентиль X очень похож на классический вентиль NOT: он преобразует |0? в |1?, а |1? в |0?. Эта операция эквивалентна повороту вектора на сфере Блоха вокруг оси x на ? радиан (или 180°).

Вентиль Y ожидаемо соответствует повороту вектора вокруг оси y на ? радиан. В результате такой операции вектор |0? превращается в i|1?, а |1? — в -i|0?.

Вентиль Z представляет собой особый случай вентиля фазового сдвига (см. ниже) при фи = ? = 180°. Он соответствует повороту вектора вокруг оси z на ? радиан. Вектор |0? он оставляет без изменений, а |1? преобразует в -|1?.

Ниже работа этих преобразований проиллюстрирована с помощью сферы Блоха (ось вращения в каждом случае выделена красным; на картинку можно нажать, чтобы увеличить ее):



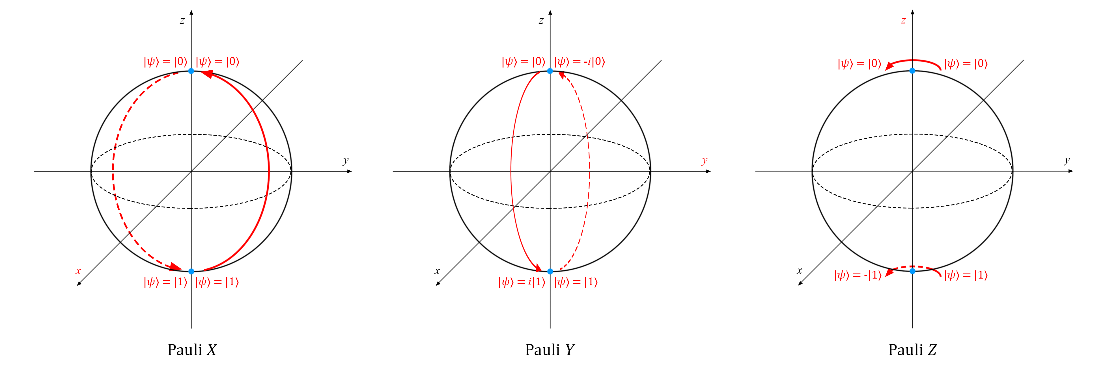
Важно отметить, что после двукратного применения одного и того же вентиля Паули к кубиту он перейдет в исходное состояние (потому что после поворота вектора на 2? радиан или 360° вокруг любой оси он перейдет в начальное положение). Как следствие,



Поскольку и т. д.,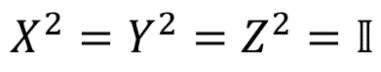

Здесь II — обозначение единичной матрицы: 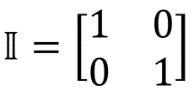. Единичной называется матрица, результат умножения которой на произвольную матрицу M (II) равен матрице M: MII = IIM = M. Единичная матрица соответствует квантовой операции, которая не меняет квантовое состояние. На сфере Блоха это выглядит так: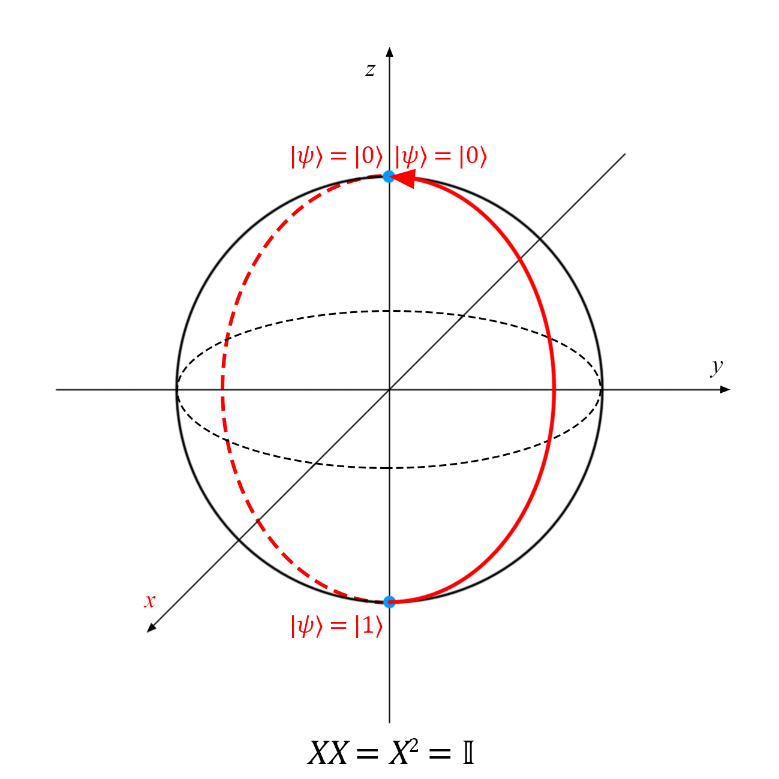



Ввиду этого отношения говорят, что матрица Паули в квадрате равна единичной матрице.
Ниже приводится описание еще нескольких важных однокубитных вентилей.

Названия	Матричное представление	Обозначения	Представление в Q#
Вентиль Адамара, H		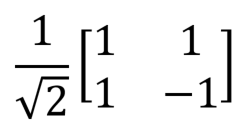	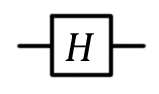H(qubit: Qubit)
Фазовый сдвиг,	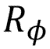		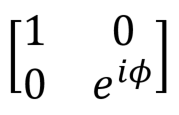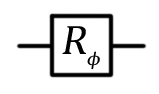R1(theta: Double, qubit: Qubit) В более общем случае R(pauli: Pauli, theta: Double, qubit: Qubit)
Фазовый сдвиг,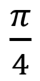, S		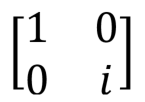	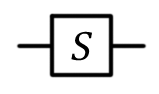S(qubit: Qubi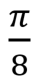t)
, T		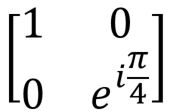	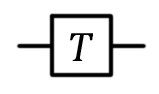T(qubit: Qubit)

Вентиль Адамара особенно важен, потому что с его помощью можно создать суперпозицию состояний |0? и |1?. Эту операцию проще всего визуализировать с помощью сферы Блоха как поворот вокруг оси x на ? радиан (180°) с последующим поворотом вокруг оси y (по часовой стрелке) на ?/2 радиан (90°):



Вентиль фазового перехода представляет достаточно общую операцию, у которой есть множество полезных применений. Самые распространенные его вариации — вентили сдвига фазы на ?/4, ?/8 и Паули-вентиль Z, для которых параметр фи равен ?/2, ?/4 и ? соответственно. Пример фазового сдвига на сфере Блоха:

Многокубитные вентили

Многокубитные вентили выполняют операции над двумя или более кубитами. Один из простейших примеров — вентиль SWAP:

Названия	Матричное представление	Обозначения	Представление в Q#
SWAP		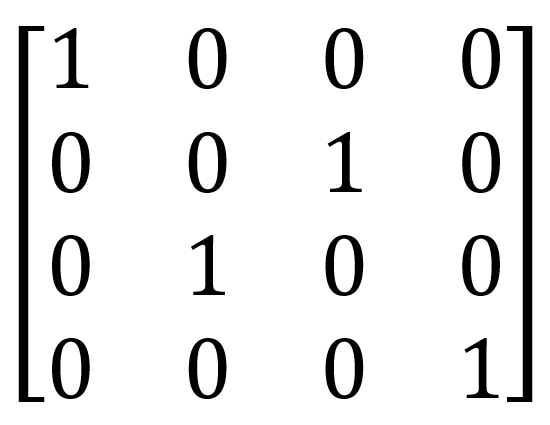	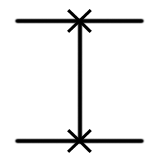SWAP(qubit1: Qubit, qubit2: Qubit)

Вентиль SWAP меняет местами два входных кубита. Например, SWAP|0?|1? = |1?|0?, а SWAP|0?|0? = |0?|0? (полная таблица истинности приводится в шпаргалке по цепям).

Еще один класс многокубитных вентилей — так называемые управляемые вентили. На вход любого управляемого вентиля подается по меньшей мере один управляющий и один управляемый кубит, причем вентиль выполнит операцию над управляемым кубитом только в том случае, если управляющий кубит находится в определенном состоянии.

Вентили, которые выполняют операцию при управляющем кубите |1?, обозначаются заполненным кругом на проводе управляющего кубита. Вентили, которые выполняют операцию при управляющем кубите, равном |0?, обозначаются пустой окружностью, как показано ниже.



Для того чтобы составить матрицу любого управляющего вентиля, нужно дописать единичную матрицу в левом верхнем углу матрицы нужного вентиля, а все остальные ячейки заполнить нулями. Вот пример:



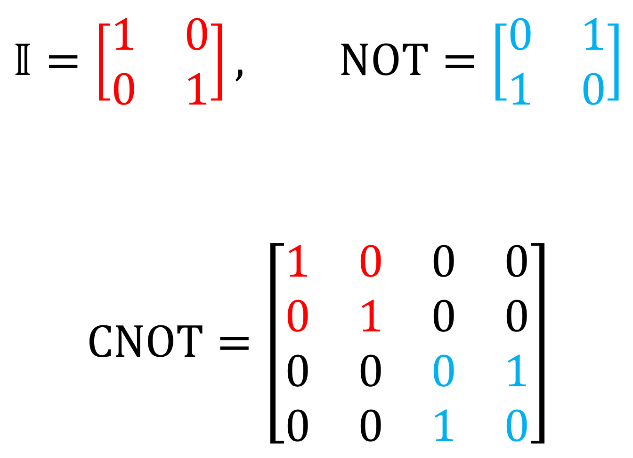
Обычные вентили в Q# можно преобразовать в управляющие с помощью ключевого слова Controlled, как описано здесь (в разделе «Controlled» в самом низу страницы). Например, вентиль CNOT (напомним, что вентиль NOT эквивалентен X-вентилю Паули) можно получить командой

(Controlled X)([control], (target))

где [control] — массив входных управляющих кубитов.

Ниже описаны другие распространенные управляемые вентили (мы выделили единичную матрицу красным, а матрицу исходного вентиля — синим, как выше):

Названия	Матричное представление	Обозначения	Представление в Q#
CNOT			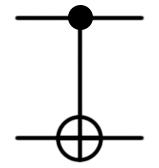CNOT(control: Qubit, target: Qubit) или (Controlled X)([control], (target));
CCNOT, вентиль Тоффоли			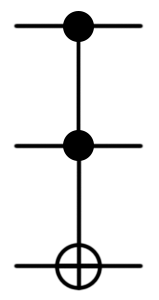CCNOT(control1: Qubit, control2: Qubit, target: Qubit) или (Controlled X)([control1; control2], target);
CSWAP, вентиль Фредкина			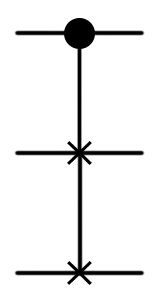(Controlled SWAP)([control], (target));

Универсальные наборы

Как мы уже упоминали в предыдущей публикации, вне зависимости от того, с помощью какой физической системы мы имитируем квантовый компьютер, должна иметься возможность реализовать «универсальный набор» вентилей. Это значит, что любая допустимая вычислительная операция в нашей системе должна быть преобразуема к конечной последовательности известных вентилей. Вот пример такого универсального набора: вентиль Адамара, вентиль фазового сдвига, вентиль CNOT и вентиль ??8.

Свойство универсальности гораздо интереснее, чем может показаться на первый взгляд. Если в квантовом компьютере существует универсальный набор вентилей, то любое преобразование, которое допускают законы квантовой физики, можно реализовать с его помощью. Это значит, что с помощью универсального набора можно не просто выполнить любую квантовую программу, а имитировать любое физическое явление. Поэтому свойство универсальности позволяет использовать квантовые компьютеры для моделирования молекул, сверхпроводников и любых странных и прекрасных квантовых систем. Эта особенность квантовых компьютеров позволяет имитировать физические явления, что в перспективе позволит квантовым системам превзойти потенциал самых мощных суперкомпьютеров. Уже не скучно, правда?

Нас ждет еще много интересного!

С помощью этих (и некоторых других) важнейших вентилей уже можно создавать полнофункциональные квантовые цепи! В следующей публикации я расскажу, как с помощью этих новоприобретенных знаний можно реализовать квантовое преобразование Фурье — очень важную операцию, у которой есть огромное множество практических применений.

Дополнительные ресурсы

• Microsoft Quantum
• Microsoft Quantum Development Kit
• Блог Microsoft Quantum