Возможно, вы узнали о выпуске пакета средств квантовой разработки Quantum Development Kit и подумали, что это звучит безумно круто… а потом вспомнили, что про квантовую механику почти ничего не знаете. Но ничего страшного. Через 30 минут вы будете знать о кубитах, суперпозиции и квантовой запутанности достаточно, чтобы написать свою первую программу и, что более важно, неплохо понимать, что она делает.



Франчес — выпускница Имперского колледжа Лондона с научной степенью в области вычислительных технологий. Она написала свой дипломный проект, работая в подразделении Microsoft Research. Сейчас Франчес работает в Microsoft на должности инженера программных решений. Основные направления ее деятельности — машинное обучение, большие данные и квантовые вычисления.

Содержание статьи

• Повторим основы
• Измеряем кубит
• Квантовые вентили
• Важные вентили
• Несколько кубитов
• Еще один важный вентиль
• Состояние Белла
• Пишем квантовую программу
• Что дальше?
• Приложение
• Дополнительные материалы

Повторим основы

Если вы не программируете на самом низком уровне, то вполне можете забыть, что любые программы, по сути, лишь манипулируют нулями и единицами, которые хранятся в наших «классических» компьютерах. Этим нулям и единицам соответствуют дискретные бинарные состояния физических систем. Квантовые компьютеры работают с непрерывными диапазонами состояний. Отчасти их возможности обусловлены именно этим.

Классический бит может принимать только одно из двух состояний — «включено» или «выключено», как обычная лампа накаливания. Кубиты, основа квантовых компьютеров, больше похожи на светильник с регулировкой яркости.



Для записи двух состояний кубитов можно использовать обозначения бра и кет (обозначения Дирака), которые соответствуют следующим векторам:



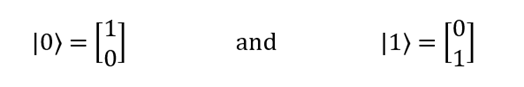
С помощью линейной комбинации этих двух состояний можно выразить любое возможное сочетание векторов |0? и |1?. В квантовой механике такое сочетание называется суперпозицией. Соответствующая запись в обозначениях Дирака будет выглядеть так:

|?? = ? |0? + ? |1?

Величины ? и ? связаны с вероятностями (с одним небольшим отличием — эти коэффициенты могут выражаться комплексными числами). Можно считать их действительными числами, но в этом случае помните, что они могут принимать отрицательные значения. Однако сумма их квадратов всегда равна 1.

Измеряем кубит

Квантовые состояния — странная штука. В результате измерения (или, как говорят, «в присутствии наблюдателя») кубит немедленно коллапсирует. Как это понимать? Предположим, кубит находится в состоянии суперпозиции. Если его измерить, то он примет одно конкретное значение — |0? или |1? (сразу оба результата одно измерение показать не может!). После измерения кубита коэффициенты ? и ?, которыми характеризовалось его предыдущее состояние, будут, по сути, утеряны.

Поэтому для описания измерений кубитов используется аппарат теории вероятностей. В общем случае вероятность того, что измерение состояния кубита покажет результат |0?, равна , а вероятность получить состояние |1? равна 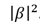. Рассмотрим пример. Пусть у нас есть следующий кубит: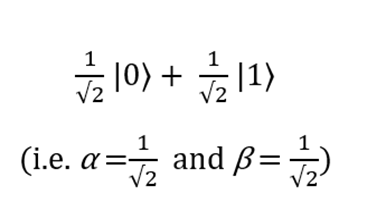



Если мы будем измерять его состояние, то в 50 % случаев будем получать значение 0, потому что:



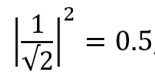
То есть после измерения он будет находиться в состоянии |0? (то есть ? = 1, ? = 0). По той же причине вероятность получить состояние 1 составляет 50 %. В этом случае после измерения кубит перейдет в состояние |1? (то есть ? = 0, ? = 1).



В первый раз все это сильно сбивает с толку (на второй, третий и четвертый раз ничего не изменится). Основная идея здесь заключается в том, что вероятностные квантовые состояния можно использовать для вычислений, и в некоторых случаях эта их квантовая «странность» позволяет получить системы с эффективностью выше классических. Теперь посмотрим, как эти кубиты можно использовать для вычислений, подобно классическим битам.

Квантовые вентили

Вернемся пока к более привычным вещам. В классической теории вычислений для выполнения операций над битами используются логические вентили. Для манипуляций над кубитами применяются аналогичные конструкции — квантовые вентили. Например, вентиль NOT выполняет преобразования 0 > 1 и 1 > 0. Квантовый вентиль NOT похож на своего классического предка: он выполняет преобразования |0? > |1? и |1? > |0?. Это значит, что после прохождения такого вентиля кубит из состояния ? |0? + ? |1? перейдет в состояние ? |1? + ? |0?. Вентиль NOT можно записать в виде матрицы (X), которая меняет местами 0 и 1 в матрице состояния:



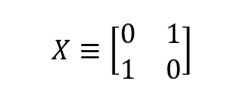
Как видим, X|0? = |1?, а X|1? = |0?:



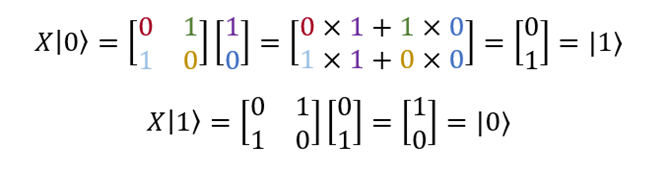
Поскольку |0? и |1? в векторной форме записываются как 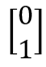и , первый столбец матрицы X можно рассматривать как преобразование вектора |0?, а второй — как преобразование вектора |1?.

Казалось бы, отличие от классического случая не столь велико. Но не забывайте, о чем мы говорили в предыдущем разделе: измерение состояния кубита носит вероятностный характер. Как известно из элементарной теории вероятностей, сумма вероятностей полной группы несовместных событий равна единице. Поэтому 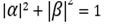для квантового состояния ? |0? + ? |1?.

Отсюда следует, что в квантовом мире могут существовать не все мыслимые вентили. Вот одно из ограничений: условие нормализации квантового состояния кубита, , должно соблюдаться как до прохождения вентиля, так и после него. В терминах матричной алгебры это условие будет выполнено в том случае, если матрица является унитарной.

Я постараюсь объяснить, что означает математическое понятие унитарности. Если прочитать его достаточно быстро, вы просто окажетесь на следующем предложении. Вентиль называется унитарным, если получена путем транспонирования и комплексного сопряжения и является единичной матрицей ранга 2. Если говорить человеческим языком, это означает, что преобразование не меняет длину вектора. Если длина вектора не меняется со временем, то сумма всех вероятностей неизменно равна единице, или 100 % (как и должно быть). Выкладки, в результате которых сумма всех вероятностей оказывается равной 200 % или 25 %, были бы лишены смысла. Унитарные матрицы защищают по крайней мере от такого безумия (хотя в квантовом мире его остается предостаточно).

Хорошие новости: это ограничение является единственным. Ввиду этого условия у некоторых классических вентилей нет квантового аналога, однако и у некоторых квантовых вентилей нет классического прототипа. Далее мы разберем важнейшие из квантовых вентилей.

Важные вентили: вентиль Z и вентиль Адамара

Описанные ниже вентили будут использоваться в нашей первой квантовой программе, поэтому постарайтесь их запомнить. Вентиль Z работает очень просто: он сохраняет компонент |0? и меняет знак компонента |1?. Его можно записать в виде матрицы



которая преобразует состояния кубитов следующим образом: |0? > |0?, |1? > -|1? (помните, что первый столбец матрицы описывает преобразование вектора |0?, второй — преобразование вектора |1?).

Вентиль Адамара создает суперпозицию состояний |0? и |1?, подобных рассмотренным выше. Его матричная запись выглядит так:



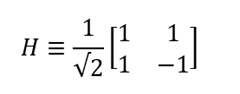
что соответствует следующим преобразованиям состояний кубитов: ,

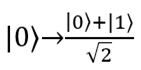Более подробная информация об унитарных матрицах и о способах наглядного представления вентилей приводится в ресурсах, ссылки на которые содержатся в разделе «Дополнительные материалы».

Несколько кубитов

Рассмотрим нечто более привычное. Классические биты существуют не только поодиночке, но и в виде сочетаний: например, 00, 01, 10 и 11. В квантовых вычислениях используются аналогичные комбинации: |00?, |01?, |10? и |11?. Состояние двух кубитов можно описать с помощью следующего вектора:



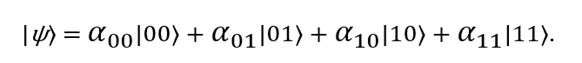
Как и раньше, вероятность получить в результате измерения величину 00 равна ,
для 01 вероятность равна 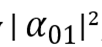и т. д.

Допустим теперь, что мы хотим измерить состояние не обоих кубитов, а только первого. Вероятность получить при этом 0 равна 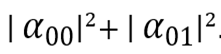. Как мы помним, измерение меняет состояние, поэтому после него вектор будет иметь значение



Обратите внимание на числитель: мы убрали все слагаемые, для которых первый бит равен 1 (поскольку по условию результат измерения равен 0). Для того чтобы вектор описывал допустимое квантовое состояние, необходимо, чтобы квадрат сумм амплитуд был равен единице (как до, так и после преобразования). Чтобы это условие выполнялось, мы добавляем нормировочный множитель — величину, обратную квадратному корню из определителя.

Еще один важный вентиль

Работу вентиля NOT мы уже разобрали. Следующий на очереди — вентиль CNOT (controlled-NOT, «управляемое НЕ»). На его вход подается два кубита. Первый называется управляющим, второй — управляемым. Если управляющий кубит равен |0?, то состояние управляемого кубита не меняется. Если управляющий кубит равен |1?, то к управляемому кубиту применяется операция NOT.

Операцию CNOT можно интерпретировать несколькими способами. Подобно вентилям X, Z и H, ее можно записать в матричной форме, которая обозначается буквой U.



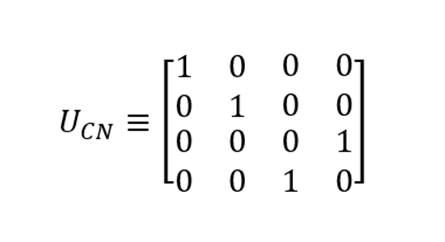
Можно заметить, что столбцы матрицы соответствуют следующим преобразованиям: |00? > |00?, |01? > |01?, |10? > |11?, |11? > |10?. Как и матрицы, которые мы разобрали в , она является унитарной, а значит, .

Также для этого вентиля используется следующее обозначение (верхняя часть соответствует управляющему кубиту, нижняя — управляемому):



Выглядит как экспонат выставки современного искусства.

Состояния Белла

Этой важной теме стоит посвятить целый раздел. Всего существует четыре состояния Белла. Одно из них (|?+?) будет использоваться в квантовой программе ниже. Давайте его рассмотрим.



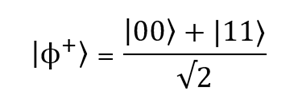
Допустим, мы измеряем состояние первого кубита. Результат |0? мы получим с вероятностью 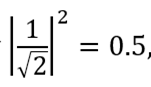. Это означает, что состояние после измерения |?’ ? = |00?, или |1? с той же вероятностью (0,5), а состояние после измерения |?’ ? = |11?. Для любознательных приводим полный набор состояний Белла (они представляют собой простейшие случаи квантовой запутанности):



Теперь предположим, что мы измерили состояние второго кубита. Согласно тем же рассуждениям, после измерения пара будет находиться в состоянии |00? или |11?. Если после этого мы решим измерить состояние первого кубита, вероятности уже не будут равны 0,5. Мы получим |0? с вероятностью 1 или 0 — в зависимости от того, каким был результат измерения. Здесь важно понять, что эти результаты связаны между собой. Первыми это заметили Альберт Эйнштейн, Борис Подольский и Натан Розен (поэтому эти состояния иногда называют «парами ЭПР»). Впоследствии их теорию развил Джон Белл.

И последнее наблюдение: состояния Белла можно генерировать с помощью вентиля Адамара и вентиля CNOT. По-моему, это достойно восхищения. Вентиль Адамара переводит первый кубит в состояние суперпозиции. Затем этот кубит подается на управляющий вход вентиля CNOT. Вот как этот процесс можно представить с помощью диаграммы цепи:



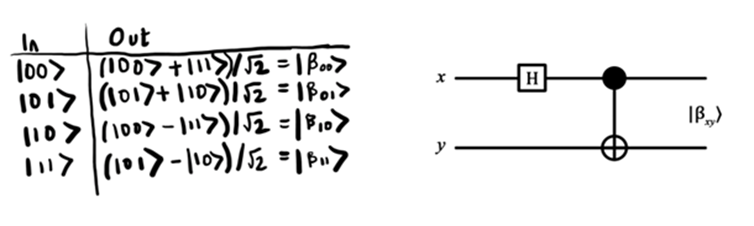
Чтобы узнать подробнее, как работает каждое из этих преобразований, обратитесь к дополнительным материалам (список приводится ниже). Мы уже знаем о состояниях кубитов, квантовых вентилях и состояниях Белла достаточно, чтобы написать нашу первую программу с использованием кубитов.

Пишем квантовую программу

Мы будем следовать инструкциям из документации.

Это учебное руководство поможет вам выполнить следующие действия: установить пакет разработки квантовых программ (этапы 1–2), выделить кубит и выполнить над ним ряд простых манипуляций — например, установить его в некоторое состояние и измерить его (этапы 3–5), затем перевести кубит в состояние суперпозиции (этап 6), а после этого преобразовать два кубита в запутанное состояние — состояние Белла, или пару ЭПР (этап 7).

Рекомендуется следовать инструкциям из руководства, ссылка на которое приведена выше, и возвращаться к этому материалу, если вам нужны советы или дополнительные пояснения.

Этап 1. Создание проекта и решения

Q# находится в нижней части этого списка.

Этап 2 (необязательный). Обновление пакетов NuGet

Мы последовали этому совету, но делать это необязательно, особенно если вы любите рисковать.

Этап 3. Ввод кода Q#

namespace Quantum.Bell
{
    open Microsoft.Quantum.Primitive;
    open Microsoft.Quantum.Canon;

    operation Set (desired: Result, q1: Qubit) : ()
    {
        body
        {
            let current = M(q1);
            if (desired != current)
            {
                X(q1);
            }
        }
    }
}

Эта операция переводит наш кубит в выбранное (нами) состояние — 0 или 1. Вначале мы измеряем кубит (эта операция обозначается буквой M), и он коллапсирует в состояние 0 или 1. Если измеренное состояние не соответствует желаемому, мы меняем его с помощью вентиля NOT, X. В противном случае ничего делать не надо.

operation BellTest (count : Int, initial: Result) : (Int,Int)
    {
        body
        {
            mutable numOnes = 0;
            using (qubits = Qubit[1])
            {
                for (test in 1..count)
                {
                    Set (initial, qubits[0]);

                    let res = M (qubits[0]);

                    // Count the number of ones we saw:
                    if (res == One)
                    {
                        set numOnes = numOnes + 1;
                    }
                }
                Set(Zero, qubits[0]);
            }
            // Return number of times we saw a |0> and number of times we saw a |1>
            return (count-numOnes, numOnes);
        }
    }

Этот небольшой фрагмент кода предназначен для тестирования операции, которую мы только что написали. Это очень простая программа: она проверяет, что кубит был переведен в нужное нам состояние.

Для этого она в цикле проводит измерение и подсчитывает количество результатов 1 с помощью переменной numOnes.

Запись «Qubit[1]» означает «создать массив кубитов из одного элемента». Индексация элементов массива ведется с нуля. Чтобы выделить два кубита (позже нам потребуется это сделать), нужно записать «Qubit[2]». Кубитам в таком массиве соответствуют номера 0 и 1.

В цикле for мы устанавливаем кубит, выделенный для определенного начального состояния, — One или Zero (в файле Driver.cs, к которому мы скоро перейдем, это делается в явном виде). Мы измеряем это состояние, и если это One, увеличиваем значение счетчика на единицу. Затем функция возвращает количество наблюдаемых состояний One и Zero. В конце кубит переводится в состояние Zero (просто чтобы оставить его в некотором известном состоянии).

Этап 4. Ввод кода драйвера C#

            using (var sim = new QuantumSimulator())
            {
                // Try initial values
                Result[] initials = new Result[] { Result.Zero, Result.One };
                foreach (Result initial in initials)
                {
                    var res = BellTest.Run(sim, 1000, initial).Result;
                    var (numZeros, numOnes) = res;
                    System.Console.WriteLine(
                        $"Init:{initial,-4} 0s={numZeros,-4} 1s={numOnes,-4}");
                }
            }
            System.Console.WriteLine("Press any key to continue...");
            System.Console.ReadKey();

В этом драйвере создается квантовый симулятор и массив начальных значений, которые нужно проверить (Zero и One). Затем симуляция повторяется 1000 раз, а результат для отладки выводится на экран с помощью функции System.Console.WriteLine.

Этап 5. Сборка и выполнение

Init:Zero 0s=1000 1s=0
Init:One 0s=0 1s=1000
Press any key to continue...

Если все в порядке, вывод на экран должен выглядеть так, как показано выше. Этот результат означает, что если мы переведем начальный кубит в состояние Zero и проведем тысячу повторов, то количество состояний |0? по результатам наблюдения будет равно 1000. То же самое должно выполняться для состояния One.

Этап 6. Создание суперпозиции

Попробуем нечто более интересное. Здесь мы меняем состояние кубита с помощью вентиля NOT.

                    X(qubits[0]);
                    let res = M (qubits[0]);

Затем запускаем программу заново и видим, что результаты стали обратными.
Init:Zero 0s=0 1s=1000
Init:One 0s=1000 1s=0


Затем вентиль NOT заменяем на вентиль Адамара (H). В результате, как мы знаем, кубит перейдет в суперпозицию состояний, и результат его измерения может быть равен как |0?, так и |1?, с некоторой вероятностью.

                    H(qubits[0]);
                    let res = M (qubits[0]);

Если запустить программу снова, мы получим довольно интересный результат.
Init:Zero 0s=484 1s=516
Init:One 0s=522 1s=478

Количество результатов измерений |0? и |1? будет примерно равно.

Шаг 7. Подготовка запутанного состояния

Сейчас мы создадим состояние Белла. Изучите приведенный ниже код. Вначале мы создаем массив из двух кубитов (Qubit[2]). Первый кубит (на предыдущей диаграмме цепи он обозначался символом x) мы переводим в некоторое начальное состояние, а второй (y на диаграмме) устанавливаем в состояние Zero. Это примерно то же самое, что ввод |00? либо |10? в зависимости от X:

operation BellTest (count : Int, initial: Result) : (Int,Int)
    {
        body
        {
            mutable numOnes = 0;
            using (qubits = Qubit[2])
            {
                for (test in 1..count)
                {
                    Set (initial, qubits[0]);
                    Set (Zero, qubits[1]);

                    H(qubits[0]);
                    CNOT(qubits[0],qubits[1]);
                    let res = M (qubits[0]);

                    // Count the number of ones we saw:
                    if (res == One)
                    {
                        set numOnes = numOnes + 1;
                    }
                }

                Set(Zero, qubits[0]);
                Set(Zero, qubits[1]);
            }
            // Return number of times we saw a |0> and number of times we saw a |1>
            return (count-numOnes, numOnes);
        }
    }

В соответствии с диаграммой первый кубит, qubits[0], нужно пропустить через вентиль Адамара. В результате он окажется в суперпозиции. Затем пропускаем кубиты через вентиль CNOT (qubits[0] — управляющий кубит, qubits[1] — управляемый) и измеряем результат.

Чтобы понять, какой результат следует ожидать, повторим еще раз, как работает наше состояние Белла. Если измерить первый кубит, мы получим значение |0? с вероятностью 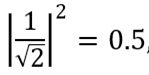. Это значит, что состояние после измерения |?’ ? = |00? или |1? с одинаковыми вероятностями (0,5), а состояние после измерения |?’ ? = |11?. Таким образом, результат измерения состояния второго кубита будет равен |0?, если первый кубит находился в состоянии |0?, и |1?, если первый кубит был в состоянии |1?. Если состояния двух кубитов были успешно запутаны, то наши результаты должны показывать, что первый и второй кубит находятся в одинаковых состояниях.

В нашем коде мы проверяем, равен ли результат измерения qubits[1] результату измерения qubits[0], с помощью оператора if.

operation BellTest (count : Int, initial: Result) : (Int,Int,Int)
    {
        body
        {
            mutable numOnes = 0;
            mutable agree = 0;
            using (qubits = Qubit[2])
            {
                for (test in 1..count)
                {
                    Set (initial, qubits[0]);
                    Set (Zero, qubits[1]);

                    H(qubits[0]);
                    CNOT(qubits[0],qubits[1]);
                    let res = M (qubits[0]);

                    if (M (qubits[1]) == res) 
                    {
                        set agree = agree + 1;
                    }

                    // Count the number of ones we saw:
                    if (res == One)
                    {
                        set numOnes = numOnes + 1;
                    }
                }

                Set(Zero, qubits[0]);
                Set(Zero, qubits[1]);
            }
            // Return number of times we saw a |0> and number of times we saw a |1>
            return (count-numOnes, numOnes, agree);
        }
    }

Перед тем как проверить результаты, нужно внести в файл Driver.cs еще одно изменение: добавить переменную agree.

using (var sim = new QuantumSimulator())
            {
                // Try initial values
                Result[] initials = new Result[] { Result.Zero, Result.One };
                foreach (Result initial in initials)
                {
                    var res = BellTest.Run(sim, 1000, initial).Result;
                    var (numZeros, numOnes, agree) = res;
                    System.Console.WriteLine(
                        $"Init:{initial,-4} 0s={numZeros,-4} 1s={numOnes,-4} agree={agree,-4}");
                }
            }
            System.Console.WriteLine("Press any key to continue...");
            System.Console.ReadKey();

Теперь программу можно запускать. Что означают эти результаты? Если первый кубит изначально был помещен в состояние Zero (то есть на вход мы подали значение |00?), то вентиль Адамара переводит кубиты в состояние суперпозиции, и результат измерения равен |0? в 50 % случаев и |1? в 50 % случаев. Выполнение этого условия можно оценить по количеству нулей и единиц. Если бы измерение состояния первого бита не влияло на состояние второго, то оно оставалось бы равным |0?, и согласованность достигалась бы только в 499 случаях.

Но, как мы видим, состояния первого и второго кубита полностью согласуются: количество результатов |0? и |1? (примерно) совпадают. Таким образом, результаты согласованы в каждом из 1000 случаев. Именно так и должны работать состояния Белла.
Init:Zero 0s=499 1s=501 agree=1000
Init:One 0s=490 1s=510 agree=1000

На этом мы закончим. Вы написали свою первую квантовую программу и (раз уж вы добрались до конца), вероятно, поняли, что именно она делает. Это стоит отметить хорошей чашкой чая.

Что дальше?

В репозитории GitHub доступно множество примеров.

В следующей статье мы поговорим о теории квантовой телепортации и изучим пример кода.

Квантовые вентили рассматриваются подробнее в блоге Аниты (примечание: Анита просто потрясающая).

Дополнительные материалы

Если вы хотите углубиться в рассмотренные темы, ниже приводится список ресурсов, которые были для нас очень полезными. Первый из них — книга «Квантовые вычисления и квантовая информация» (М. Нильсен, И. Чанг). Второй — документация к пакету SDK от Microsoft.

Если это будет интересно читателям (оставьте комментарий!), мы можем составить отдельную публикацию о других ресурсах.

Приложение. Состояния Белла

Генерировать состояния Белла можно с помощью вентиля Адамара и вентиля CNOT. Вентиль Адамара переводит первый кубит в состояние суперпозиции. Затем этот кубит подается на управляющий вход вентиля CNOT. На диаграмме цепи это выглядит так:
Начнем с первого случая, когда на вход подается пара кубитов в состоянии |00?. Первый кубит, |0?, проходит через вентиль Адамара и превращается в . Второй кубит при этом не меняется. Результат: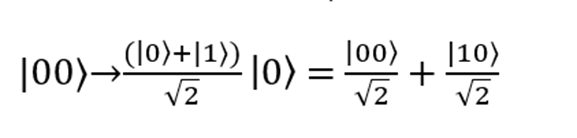



Затем кубиты проходят через вентиль CNOT (который выполняет преобразования |00? > |00? и |10? > |11?). Теперь их состояние будет описываться формулой



Второй случай: на вход подаются кубиты |01?. Вентиль Адамара переводит первый кубит |0? в состояние . Второй кубит не меняется. Результат: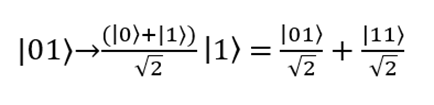



Теперь пропустим кубиты через вентиль CNOT, который выполняет преобразования |01? > |01? и |11? > |10?. Итоговое состояние пары кубитов будет выглядеть так:



Третий случай: на вход подаются кубиты |10?. Вентиль Адамара переводит первый кубит |1? в состояние . Второй кубит не меняется. Результат:



Затем кубиты проходят через вентиль CNOT (который выполняет преобразования |00? > |00? и |10? > |11?). Теперь их состояние будет описываться формулой



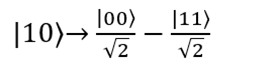
Четвертый случай: на вход подаются кубиты |11?. Вентиль Адамара переводит первый кубит |1? в состояние 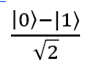. Второй кубит не меняется. Результат:



Теперь пропустим кубиты через вентиль CNOT, который выполняет преобразования |01? > |01? и |11? > |10?. Итоговое состояние пары кубитов будет выглядеть так:



Готово, мы разобрали все случаи.