Давным-давно, когда диоды были ещё вакуумными, J. В. Johnson впервые наблюдал мерцательный эффект в токе электронных ламп, который он так и назвал – мерцательным или фликкер-шумом. Прошло ровно 90 лет с тех пор, а фликкер-шум продолжают обнаруживать в самых разнообразных системах – от полупроводниковых приборов до разлива рек, от физики до социологии, но объяснить природу его происхождения так никто и не смог.
Даже советский фильм есть про фликкер-шум.
Вот как выглядит фликкер-шум:
Физики, пытаясь объяснить природу данного явления, естественно, ищут её в физике протекающих процессов, хотя и называют фликкер-шум аномалией. Вспомним, чему нас учат в аспирантуре на курсах по «Истории и философии науки»: аномалия (чем и является фликкер-шум) — это результат принципиальной неспособности научной парадигмы объяснить существующие факты, то есть проблему необходимо искать в теории.
Теорией в данном случае являются спектральные методы. Попробуем разобраться с этими методами, может с ними что-то не так?
По определению, фликкер-шум является сигналом, спектральная плотность мощности (или просто спектр мощности) которого описывается формулой:
где K – размерная константа, ? – безразмерная константа, которая в большинстве случаев близка к единице (в статье будем рассматривать только фликкер-шум с ? = 1).
Посмотрим на спектр мощности фликкер-шума и попробуем в нём что-нибудь увидеть.
Видно, что мощность в полосе частот от 1 Гц до бесконечности равна мощности от 0 до 1 Гц. Что такого особенного в этих двух полосах частот, что мощность в них одинаковая? Эти две полосы связывает то, что их границы являются обратными величинами друг друга, то есть 0 равен 1/бесконечность, а 1 равна 1/1. А что такое обратная величина от частоты? Это период.
Интересно, а почему в спектральном анализе используется только спектральная плотность мощности по частоте, может стоит попробовать найти спектральную плотность мощности по периоду? На этом месте все говорят – «зачем нужно от периода находить, от этого ничего не изменится». Посмотрите на рисунок.
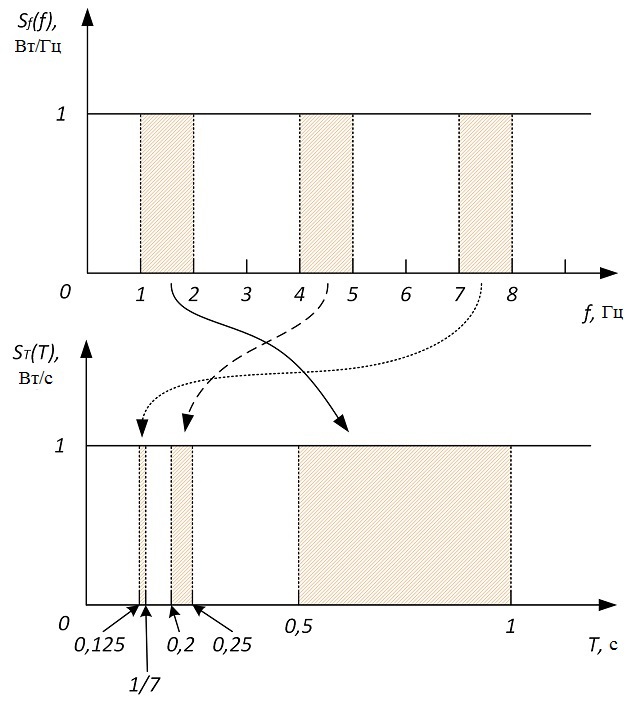
Из рисунка видно, что одной и той же полосе частот соответствуют разные полосы периодов. Значит, спектр мощности по периоду должен быть совсем другой формы. Найдём связь между спектральными плотностями мощности по частоте и по периоду. Элементарное приращение мощности равно:
где Sf(f) – спектральная плотность мощности по частоте (f-СПМ), ST(f) – спектральная плотность мощности по периоду (T-СПМ), T – период.
Знак минуса в правой части формулы (2) означает, что положительному приращению по частоте соответствует отрицательное приращение по периоду.
Из формулы (2) получим:
Как же теперь будет выглядеть фликкер-шум? Опять то же самое:
Фликкер-шум является единственным сигналом, спектр мощности которого выглядит одинаково как по частоте, так и по периоду. Если взять, к примеру, белый шум, то его T-СПМ не будет уже равномерной по периоду:
Какой же тогда сигнал будет равномерным по периоду? Да вот какой:
Это броуновский шум, его T-СПМ и f-СПМ, соответственно, определяются формулами:
Если представлять броуновский шум в виде суммы гармоник, то удобнее использовать тогда не ряд Фурье, а ряд с равномерным шагом по периоду:
где An — амплитуда n-ой гармоники, T1 – период основной гармоники, ?n — фаза n-ой гармоники.
Можно ещё анимацию с суммированием гармоник сделать:
Со спектральной плотностью мощности по периоду можно ещё долго экспериментировать, но будем двигаться дальше.
Одинаково равномерным по частоте и по периоду, исходя из формулы (4), может быть только сигнал, всюду равный нулю. Какой же шум тогда считать сигналом с равномерным спектром? Попробуем вообразить сигнал с равномерным спектром и при этом не привязываться к какому-либо шагу по частоте или по периоду.
Представим, что какой-то завод выпускает генераторы синусоидального напряжения фиксированной частоты и фиксированной мощности. Все выпускаемые генераторы обладают абсолютной повторяемостью по мощности генерируемого сигнала и эта мощность равна P0. Однако повторяемость по частоте отсутствует напрочь – частота у каждого генератора может быть равна любому значению от нуля до бесконечности (хоть пГц, хоть ТГц). Теперь возьмём очень большое количество таких генераторов и подадим сигналы с их выходов на сумматор.
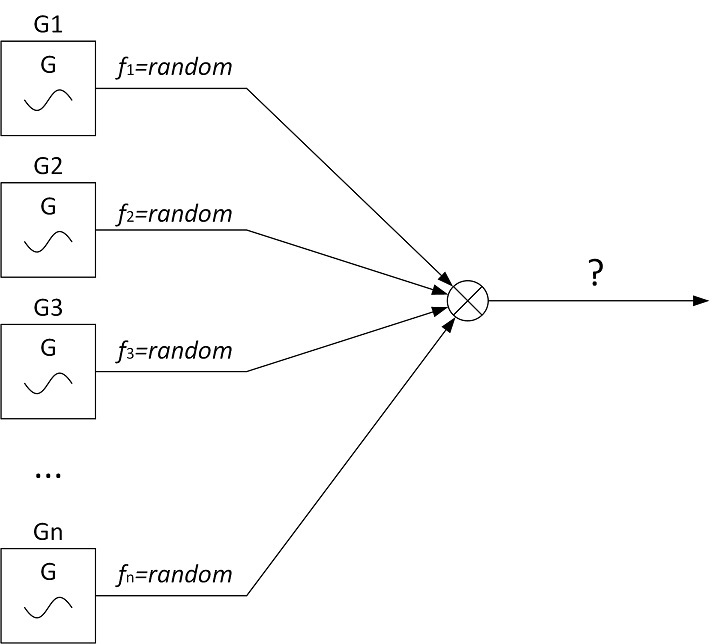
Очевидно, что сигнал на выходе сумматора должен обладать равномерным спектром. Какой же будет у него спектр мощности?
Каждый, кто знаком с основами спектрального анализа, сразу выдаст ответ – «это белый шум, так как он по определению является сигналом с равномерным спектром». Давайте это проверим.
Для начала, нужно каким-то образом связать мощность каждого генератора с его частотой. В этом месте может возникнуть вопрос – «что тут связывать, если она не зависит от частоты?», тогда встречный вопрос – от периода она тоже не зависит? В качестве такого связующего звена можно использовать энергию одного периода синусоиды:
Мощность генератора равна:
Теперь найдём функцию, которая будет показывать зависимость мощности генераторов от их частоты:
где ET(f) – зависимость энергии периода синусоиды генератора от частоты.
Мощность, приходящаяся на полосу частот df, будет равна:
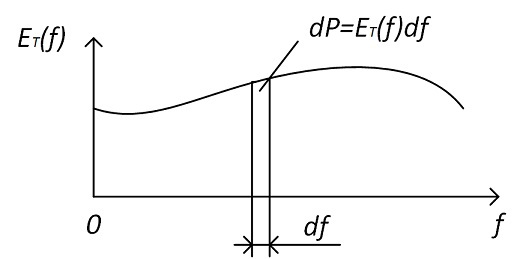
Если посмотрим на формулы (2) и (14), то мы увидим, что:
Замечательно, теперь из формулы (12) найдём спектр мощности:
Сигнал на выходе сумматора — фликкер-шум. Цвет этого шума – розовый (по мне, так он белый).
А теперь ответ на вопрос 90-летней давности:
Механизм возникновения фликкер-шума очень прост: если объект излучает гармонический сигнал произвольной частоты с мощностью P0, то множество таких объектов будет излучать сигнал со спектром фликкер-шума.
Истинный сигнал с равномерным спектром является фликкер-шумом. Любопытно, что же это за спектральная координата, относительно которой фликкер-шум выглядит равномерным.
Допустим, что генерируемые синусоиды различаются как по частоте, так и по мощности, тогда формула (16) запишется в следующем виде:
где P(f) – мощность реализации с частотой f.
Так как для процесса с равномерным спектром P(f) = P0, то P(f) удобно рассматривать как спектральную плотность мощности по некоторой величине ? (?-СПМ):
По определению, спектральная плотность мощности должна иметь размерность мощности, делённой на размерность спектральной координаты. В данном случае ?-СПМ имеет размерность мощности, следовательно, её спектральная координата ? должна быть безразмерной. Таким образом, ?-СПМ будет являться одновременно и спектральной плотностью мощности и зависимостью мощности генератора от частоты. Мощность в полосе частот df должна быть равна мощности в полосе d?:
Из формул (17), (18) и (19), получим:
и ? определится по формуле:
Для исключения логарифмирования размерной величины, примем:
где f0 – некоторая частота, равная 1 Гц,
тогда:
Совершенно бессмысленную константу f0 мне пришлось ввести из-за того, что логарифмирование размерной величины у физиков вызывает fatal error.
А теперь мы можем представить фликкер-шум в виде суммы гармоник с одинаковыми амплитудами:
где An — амплитуда n-ой гармоники, Ф1 – Ф основной гармоники, ?n — фаза n-ой гармоники.
Сделаем анимацию:
Можно ещё анимацию для одинаковых начальных фаз сделать:
Если объединим формулы (4), (17), (18), то получим красивое выражение:
Скажу ещё пару слов по квантовой механике.
Кроме спектральной плотности мощности существует ещё спектральная плотность энергии (СПЭ). Отличие их в том, что СПЭ используется для процессов с конечной энергией, а СПМ для процессов с бесконечной энергией. СПЭ характеризует энергию, приходящуюся на единицу полосы частот. А что нам мешает сделать тоже самое для процессов с конечной энергией? СПЭ по разным спектральным координатам будут связаны аналогичной формулой:
где Wf(f) – спектральная плотность энергии по частоте (f-СПЭ), WФ(Ф) – спектральная плотность энергии по ? (?-СПЭ), WT(T) – спектральная плотность энергии по периоду (T-СПЭ).
Левая часть формулы (26) Вам ничего не напоминает? Эту формулу можно легко преобразовать в формулу для энергии кванта.
Давайте представим, что рассматриваемые выше генераторы выдают сигналы с произвольными частотами и произвольными мощностями, но энергия этих сигналов конечна. В природе подобные генераторы, мягко говоря, очень распространены – это электроны, а генерируемые ими сигналы – это кванты энергии.
?-СПЭ на конкретной частоте равна энергии:
Если принять f-СПЭ равной постоянной Планка, то формула (29) преобразуется в формулу для энергии кванта (28).
Так как постоянная Планка не зависит от частоты, то её можно рассматривать как равномерную f-СПЭ процесса, каждая реализация которого соответствует излучению электроном одного кванта энергии с произвольной частотой.
Если поделить f-СПЭ электромагнитной волны на постоянную Планка, то можно получить зависимость числа квантов волны от частоты. И так далее…
Вывод: фликкер-шум — сигнал с равномерным спектром, спектр которого искажается преобразованием Фурье.
Буду рад любой критике по статье.
то спектр мощности такого процесса можно найти как производную P(f) по частоте:
Элементарное приращение тогда определится по формуле:
В этом случае появляется функция, равная производной зависимости энергии за период по частоте (с размерностью Дж/Гц).
Рассмотрим процесс, обладающий следующей ET(f):
Если ? = 1, то рассматриваемый процесс обладает равномерным непрерывным спектром (в соответствии с формулой (А.1)).
Определим по формуле (А.3) спектр мощности процесса, соответствующего формуле (А.5):

Обозначим:
и получим формулу (1):
Чем ближе ? к единице, тем равномернее спектр, однако K при этом уменьшается. В пределе, когда ? = 1 получается спектр мощности фликкер-шума с K = 0.
Для спектра мощности по периоду получается аналогичный результат.
Если ? = 0, то спектр мощности будет соответствовать белому шуму. Из формул (А.5) и (А.1) видно, что процесс с ? = 0 (белый шум) не обладает равномерным спектром:


Рассмотрим также сетку периодов с равномерным шагом, стремящимся к нулю. Так как периодный шаг стремится к нулю, то такая сетка периодов содержит в себе все возможные периоды и определены они в точках n*dT.
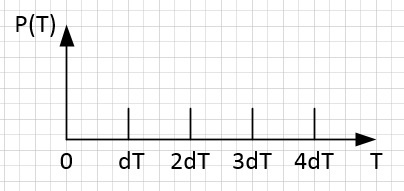
Если сопоставить сетку частот и сетку периодов, то можно увидеть, что есть периоды, которым невозможно сопоставить частоту (попадают на интервал от n*df до (n+1)*df), и наоборот.

Если частоте невозможно сопоставить период, а также если периоду невозможно сопоставить частоту, то их следует удалить из соответствующей сетки, так как они не существуют. То есть каждая сетка содержит лишние частоты и периоды. Если удалить все частоты и периоды, которым невозможно сопоставить период и частоту, то получим некоторый новый неравномерный шаг по частоте, равный неравномерному шагу по периоду. Такой шаг соответствует равномерному шагу по логарифму частоты, равный по модулю равномерному шагу по логарифму периода. Процессом, обладающим равномерным по логарифму частоты спектром, является фликкер-шум.
Коэффициенты ряда Фурье в комплексной форме определяются по формуле:
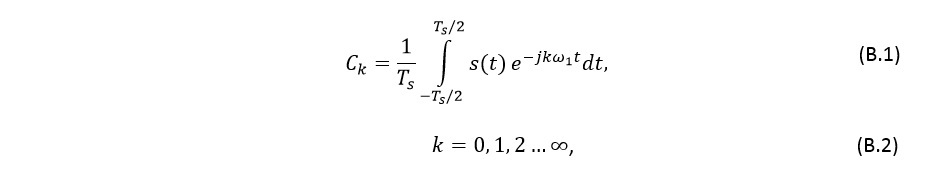
где ?1 – основная частота.
Если s(t) является дельта-функцией, то все коэффициенты Ck будут принимать одно и то же значение, независимо от k, причём значение основной частоты может быть любым.
Но ничто не мешает использовать вместо последовательности целых чисел любую другую последовательность. Если взять, например, последовательность чисел, обратную целым:
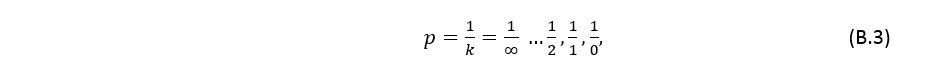
то формула (В.1) примет вид
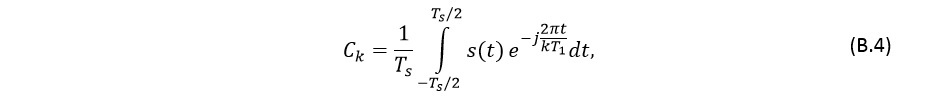
где T1 – основной период,
и будет получен дискретный спектр с равномерным шагом по периоду. В данном случае для дельта-функции значение коэффициентов Ck также принимает одно и то же значение, и значение периода основной гармоники также может быть любым.
Если перейти к непрерывным спектрам мощности по частоте и по периоду, то получим, что и тот и другой спектр мощности является независимым от своего аргумента функцией, что противоречит формуле (4). Получается, что спектр мощности дельта-функции зависит от метода его определения.
Попробуем определить, какие значения частот и периодов вообще возможны. Частота и период могут принимать любое значение от 0 до бесконечности по двум причинам:
1) Ось времени непрерывна – частоту можно увеличивать в бесконечное число раз, соответственно период можно уменьшать в бесконечное число раз.
2) Ось времени бесконечна – частоту можно уменьшать в бесконечное число раз, соответственно период можно увеличивать в бесконечное число раз.
Определим сначала спектр ограниченной во времени периодически продолженной и дискретной во временной области дельта-функции. Затем устремим к нулю шаг дискретизации и к бесконечности период повторения дельта-функции, в результате получим непрерывный спектр дельта-функции.
Известно, что периодический во временной области сигнал обладает дискретным спектром. Спектр такого сигнала представляется в виде сетки частот, полученных умножением частоты, равной f0 = 1 / (период сигнала) на целое число. В случае дельта-функции получаем набор гармоник с равномерным шагом по частоте с одинаковыми амплитудами.
Известно, что дискретный во временной области сигнал обладает периодическим спектром. Никаких ограничений на возможные значения частот нет (кроме условия, что частота в спектре должна быть меньше частоты Найквиста для восстановления).
Рассмотрим периодические дискретные сигналы:
a) Если сигнал является дискретным, то он определён только в некоторых конкретных точках: tn = n * ?t, где n – целое число, ?t – шаг дискретизации.
b) Если сигнал является периодическим, то все его значения повторяются через период времени: s(t) = s(t + T), где T – период сигнала.
c) Если сигнал является дискретным и периодическим, то все его значения повторяются через период времени, кратный шагу дискретизации s(tn) = s(tn + Td), где Td – период сигнала, являющийся суммой целого числа ?t. Это объясняется тем, что сигнал с периодом, состоящим из дробного числа ?t, через период не повторит своего значения, так как попадёт на несуществующее время. Получается, что ограничение на возможные значения частот всё же есть.
Например, если гармонический сигнал с частотой 1,5 Гц оцифровать с частотой дискретизации 10 Гц, то получается периодический сигнал с частотой 0,5 Гц.
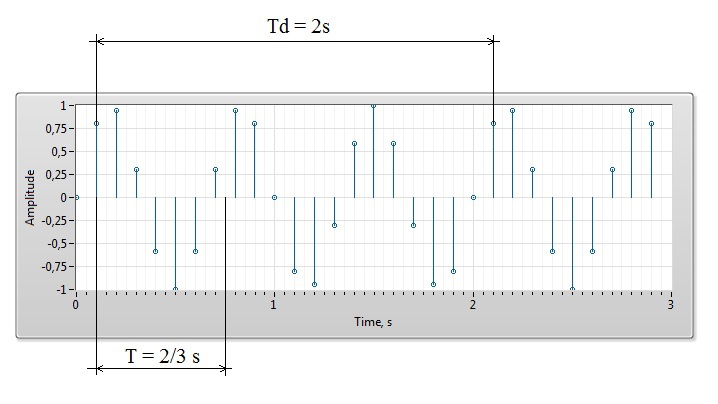
Таким образом, дискретный во времени сигнал может быть периодическим только с периодом, кратным шагу дискретизации ?t, и спектр такого сигнала может состоять только из периодов Tn = n * ?t, где n – целое число. В случае дельта-функции получаем набор гармоник с равномерным шагом по периоду с одинаковыми амплитудами.
Теперь определим спектр ограниченной во времени периодически продолженной и дискретной во времени дельта-функции. Такой спектр может состоять только из частот fn, кратных f0 и периодов Tn, кратных ?t. Если какая-то из частот fn не совпадает ни с одной из 1/Tn, то это уже не частота fn, а какая-то другая из набора 1/Tn. Таким образом, если частотe fn не удаётся сопоставить ни один из периодов из набора Tn, то её следует удалить из набора fn, так как сигнал с такой частотой нереализуем при заданном шаге дискретизации. Если удалить из сетки частот все частоты, которым невозможно сопоставить период, то получаем новый неравномерный по частоте шаг, равный неравномерному шагу по периоду. Таким неравномерным шагом является равномерный шаг по логарифму частоты. Сигналом с равномерным по логарифму частоты спектром является фликкер-шум. Если устремить к нулю шаг дискретизации и к бесконечности период повторения дельта-функций, то получаем непрерывный спектр дельта-функции, совпадающий со спектром фликкер-шума.
Комментарии (105)

ScratchBoom
07.07.2015 18:35+7Я правильно понял, что разгадка ваша? Какие горизонты в науке и технике открывает эта разгадка?

TVS Автор
07.07.2015 18:45+16Вы правильно поняли. Если в статье всё верно, то это ведёт к пересмотру основ спектрального анализа.

vanxant
07.07.2015 20:34+11Сам по себе вывод «сигнал, спектр которого искажается преобразованием разложения в спектр» звучит диковато.
Но конкретно для преобразования Фурье это не новость, а обыденная реальность — достаточно засунуть в преобразование Фурье сигнал с разрывами (ступеньками, выколотыми точками и т.п.). Формально, в момент разрыва у такого сигнала будет бесконечная мощность, и «теоретически» так как бы и не бывает. Но на практике, например, если сигнал дан нам в виде напряжения, то в момент перехода напряжения через ноль «теоретическая» мгновенная мощность сигнала может быть любой, в т.ч. сколь угодно близкой к бесконечности.
А дальше преобразование пытается разложить этот скачок в виде суммы синусоид… и обламывается, потому что как синусоиды не суммируй — они остаются непрерывными функциями и дать скачок не могут. И возникает то самое искажение спектра. Если преобразовать такой порченный сигнал назад — вместо честного разрыва получится довольно далёкая от правды кривая с выбросами. Всем известные артефакты jpeg-сжатия имеют как раз эту же природу.
Это одна из причин широкого применения вейвлетов вместо старого доброго Фурье. Так что Америку вы не открыли, при всём уважении.
А квантовые шумы действительно могут давать подобные артефакты, так как по своей природе являются прерывистыми.
slpdmn
07.07.2015 23:12+4Мне кажется вы слишком категоричны. Преобразование Фурье удобно как раз потому, что позволяет учесть «инерцию» объектов и в таком концепте анализировать сигналы. Т.к. безинерциальных объектов мы пока не имеем, то и преобразование работает корректно. Поднятый автором вопрос (насколько я понял) состоит в способе формализации объекта для приложения к нему преобразования Фурье. Это важно и правильно. Просто не надо забывать, что многие (очень многие) математические методы ограниченно пригодны для применения в инженерных задачах именно в силу того, что нужно четко понимать физический смысл этих методов. В самой же математике понятие «физический смысл» отсутствует в принципе, отсюда и рождается замеченная автором проблема.
А касательно самого фликер-шума, указанная проблема существует только в головах математиков и теоретиков от инженерии. Всем практикам всегда было ясно — хочешь уменьшить шум, уменьшай количество помех от окружающего электронного хаоса. Не будешь уменьшать — получишь белый шум, уменьшишь — получишь фликер. Этот факт сам по себе является доказательством всей приведенной математики, только, в отличие от теоретиков, он понятен любому школьнику впервые собравшему суперрегенераторный приемник на одной лампе. Что, кстати, отнюдь не уменьшает ценности анализа.

0serg
08.07.2015 15:03+1Но на практике, например, если сигнал дан нам в виде напряжения, то в момент перехода напряжения через ноль «теоретическая» мгновенная мощность сигнала может быть любой, в т.ч. сколь угодно близкой к бесконечности.
Вы пишете бред, извините. Ни один реальный сигнал «данный нам в виде напряжения» не меняется мгновенно, это азы знакомые любому работающему с сколь-либо высокочастотными сигналами, ибо это создает массу проблем когда этих переходов в секунду нужно уложить достаточно много.
Причем история знает и примеры когда время изменения напряжения было велико даже при частотах порядка герц (первые телеграфные кабели под Атлантикой) — там тоже безграмотные граждане решили что в телеграфе нет ничего сложного, как замкнул цепь — так напряжение сразу изменилось :).

Mgrin
07.07.2015 20:04А спектральную плотность мощности по периоду вы сами придумали, или это известная практика? Очень интересный подход, нигде не встречал, поиграюсь на досуге.

TVS Автор
07.07.2015 20:18+2Придумал сам (может кто-то уже и придумывал, но я не слышал). Наиболее близкое понятие — спектральная плотность по длине волны ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%82%D0%BE%D0%BA_%D0%B8%D0%B7%D0%BB%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D1%8F
Думаю, что интереснее рассматривать спектральную плотность мощности по логарифму частоты.
ignat99
07.07.2015 20:29P-адические_числа могут быть удобными для спектральной плотности мощности по логарифму частоты. IMHO он как раз обеспечивают отсутствие относительной погрешности при вычислении.

ignat99
07.07.2015 20:23Моделирование это хорошо. А есть ли возможность сделать физическую модель (радиоэлектронную например) и произвести измерения?

TVS Автор
07.07.2015 21:02Можно собрать схему из генераторов, приведённую в статье, частоты должны быть в соответствии с формулой (24). Сигнал на выходе такой схемы будет похож на фликкер-шум.

ignat99
07.07.2015 21:47Возможно стоит собрать. Если сделать реальную модель, то, вероятно можно оценить тонкости, сделать измерения и нормировать.
Например, если смотреть на Уравне?ния Навье? — Сто?кса то простые решения для вогнутой поверхности не дают дополнительных побочных завихрений, а действующая физическая модель даёт. Можно эти волны получить и на мощной вычислительной системе со специальным вычислительным алгоритмом, но физическая модель нагляднее и учитывает факторы, которые можно не заметить в теории. IMHO

slpdmn
07.07.2015 23:29Есть подозрение, что вы не все учли и при создании модели выйдет очень близкое, но все же только подобие фликер-шума. Практически, при суммировании любых шумовых сигналов имеет место взаимовлияние генераторов отдельных спектральных полос шума.

grumbler66rus
08.07.2015 08:56Такие измерения были проведены неоднократно, в том числе вашим покорным слугой :).
Берёте любой усилитель, лучше на батарейках, и подключаете ко входу высокоомное сопротивление. Записываете выходной сигнал и раскладываете его быстрым преобразованием Фурье.
ignat99
08.07.2015 10:58Начинал делать программы для дискретного быстрого преобразования Фурье на сигнальном процессоре ADSPXX в 1996 году. Я бы не стал вводить цифровое преобразование в физический опыт. Может использовать что то типа фурье-оптики.
Можно записать полную систему физических уравнений со всеми дополнительными членами и да же найти какое то решение. Возможно даже найти не тривиальное решение. IMHO Физическое моделирование быстрее и качественнее.
Может стоит к выходному сигналу добавить фильтр аналогичный преобразованию Фурье?

Bangybug
07.07.2015 21:25+2Мандельброт, кажется, этой проблемой занимался, только с другой стороны зашел.

deniskreshikhin
07.07.2015 22:17+1Круто что есть еще люди которые увлекаются такими проблемами, но есть возражения.
Во-первых, спектральный анализ и сопутствующие инструменты не могуть дать ответ на причины шумы. Для этого и вводят такие понятие как белый шум, розовый шум и т.д. Это дает возможность производить исследования не обращая внимание на природу шума.
Во-вторых, причины шума исследуются в теории динамических систем, т.е. вам следует построить некоторую динамическую систему, и доказать что она будет иметь именно такие же свойства, и что любая динамическая система которая имеет такие свойства будет ей изоморфна. Тогда вопрос будет закрыт. Но динамические системы не задаются спектрами, они задаются тройкой (T, M, ?):
In the most general sense, a dynamical system is a tuple (T, M, ?) where T is a monoid, written additively, M is a set and ? is a function
en.wikipedia.org/wiki/Dynamical_system_%28definition%29

lolmaus
07.07.2015 22:20+4Как проявляется сабж при разливе рек?

slpdmn
07.07.2015 23:21Я не автор, но уверен, что в форме берегов после разлива. Это в случае если ланшафт был создан при условиях удовлетворяющих возникновению фликер-шума. Тут кстати, может родится великолепное применение описанного метода для анализа происхождения геоструктур.

lolmaus
07.07.2015 23:24-1Что-то я не понял. Если сабж — результат математической операции над данными, то как его можно наблюдать в природе? Речь о том, что операция производится над формой русла как источником данных? Или о рендеринге виртуальных ландшафтов, в которых русла рек получаются изрезанными?

hlogeon
08.07.2015 00:15По Вашему выходит, что математические модели неприменимы в реальной социологии или психологии и вообще в реальном мире?)
Вероятность тоже можно рассматривать, как результат математических опреаций, произведенных над данными.

FreeMind2000
08.07.2015 00:52+4Смысл вот в чем:
Любой шум — это помеха.
Допустим мы хотим нарисовать разметку на дороге длинной прямой белой линией. Тогда если вместо прямой линии мы получим линию, которая через каждый примерно 1см отклоняется от идеальной прямой на ± мощность помехи (такой крюк в сантиметрах), то это будет белый шум (помеха одинакова на всех частотах Т.е. водитель засыпает очень часто или просто все время спит...).
Если мы получим линию, которая только через каждый примерно 1км отклоняется от идеальной прямой — это розовый шум, называемый в народе фликкер-шумом (помеха уменьшается с частотой, т.е водитель засыпает редко). В этом и есть смысл фликер-шума — помеха встречается редко (с малой частотой).
А вот в чем смысл фразы «Загадка фликкер-шума разгадана», я честно говоря так и не понял. Наверно в том, что автор открыл механизм возникновения фликкер-шума: Если водитель будет редко засыпать и еще реже заглядываться на барышень в коротких юбках вдоль дороги, то сумма этих двух редких «помех» даст нам фликер-шум (т.е. одну общую редко возникающую помеху состоящую из нескольких периодически возникающих помех).
Но неужели в этом и была загадка 90 летней давности? ;)
Я думаю, что никакой загадки нет, точнее она есть в головах у тех, кто пытается найти теоретическое обоснование помехи не рассматривая ее физическую природу.
P.S. Но поразмыслить на эту тему было интересно, за что автору отдельный респект.
ivlis
07.07.2015 22:51+2Вас не смущает, что Фурье-преобразование взаимооднозначно и обратимо и ничего не может исказить в принципе?

vanxant
08.07.2015 00:53+5См. мой коммент выше. Преобразование Фурье (и что хуже, не только интегральное, но и все его виды) взаимооднозначно и обратимо только в идеальном мире розовых единорогов и математиков (сарказм).
Как только в сигнале появляются а) разрывы любого рода; б) бесконечные мощности; в) шумы, в том числе бесконечно малые; г) сигнал небесконечен по оси времени или чего там (а, открою тайну, все реальные сигналы конечны, так как пока никто не прожил период лет от минус до плюс бесконечности) — так сразу вся эта взаимооднозначность и обратимость летит к чёрту.
Например, возьмите обратное Фурье от Фурье от {f=sin(x), x!=0; undef, x==0} (синус с выколотой точкой в нуле) — ну как, обратимо?
Даже теоретически, вычисление преобразования Фурье — существенно некорректно поставленная задача, если вы понимаете о чём я.
На практике, численное преобразование Фурье ещё и мерзко неустойчиво. Банально, если у вас на входе сигнал имеет разрядность 8 бит (один байт — один отсчёт), и вы считаете ДПФ «в лоб» по школьной формуле и не используете всякие модные БПФ, то для восстановления сигнала вам нужно хранить спектр в типе double (точнее даже complex<double>). Обычного complex<float> уже не хватает. Другими словами, на один байт точности сигнала вам нужно 16 байт на хранение спектра — если возьмёте меньше, вы не сможете восстановить сигнал из-за ошибок округления.
ivlis
08.07.2015 01:19Что такое undef?

splav_asv
08.07.2015 01:24Перевод: f = sin(x) для всех x кроме x == 0 и не определена в точке x == 0.
ivlis
08.07.2015 01:51Если функция не определена, то и фурье-преобразование не определено, так может быть каким угодно. Если там какая-то константа, то F[f] = delta(0) + C

vanxant
08.07.2015 02:07Ну хорошо, пусть там будет «какая-то константа», допустим, 1.
То есть, f(x) = sin(x) для любого х, кроме 0, а f(0) = 1
Возьмите прямое фурье от такой f(x).
Потом возьмите обратное фурье от того, что получится.
Вы получите исходную f(x)?
ivlis
08.07.2015 02:22+4Если там просто 1, то Фурье её просто сгладит и всё, но это некорректная физическая постановка задачи, если вам нужен бесконечно короткий всплеск, то будет так f[x] = e^ix + 1* delta(0), F[f] = delta(0) + 1.

vanxant
08.07.2015 08:35+1Да не будет там дельты (0), там будет дельта +-1, и коэффициенты всякие вы потеряли (i делить на корень из пи, вот это всё).
Пример некорректен физически, потому что это синтетический пример для младшего дошкольного возраста о том, как преобразование Фурье теряет информацию («просто сгладит и всё», ага. А потом самолёты падают).
Хотите физический пример? Их есть у меня. На практике мы не знаем f(x) на всём диапазоне от минус до плюс бесконечности. А знаем только кусочек от 0 до T. Что мы делаем? Правильно, объявляем f(x) периодической с периодом Т, получаем линейчатый спектр и вообще обратный интеграл превращается в сумму (ряд Фурье). Вот только совсем не обязательно, что f(0)=f(T). И тут получается упс — уже не просто потеря информации в особой точке, но полноценное разрушение формы сигнала на границе отрезка.
Так вот, пример. Берём всё ту же f(x)=sin(x). Но с периодом, допустим, 0.8Pi. Т.е. f(x)=sin(x mod 0.8), где mod — взятие остатка после целочисленного деления. Ну вот так у неё жизнь сложилась, не спрашивайте, почему. На практике и не такое бывает сплошь и рядом. И вот тут Фурье себя проявит во всей красе.
0serg
08.07.2015 14:38На практике мы не знаем f(x) на всём диапазоне от минус до плюс бесконечности. А знаем только кусочек от 0 до T. Что мы делаем? Правильно, объявляем f(x) периодической с периодом Т
Классический подход состоит в том чтобы просто доопределить f(x) нулем вне отрезка [0,T]. Часто используют и другие оконные функции. Зачем объявлять f(x) периодической с периодом которого у неё явно нет и удивляться потом что результат не такой который хотелось бы?!?!
Вот только совсем не обязательно, что f(0)=f(T). И тут получается упс — уже не просто потеря информации в особой точке, но полноценное разрушение формы сигнала на границе отрезка.
«Разрушение формы сигнала» будет только если Вы оборвете ряд Фурье конечным числом слагаемых. Чем больше оторвете, тем хуже будет результат, чем больше слагаемых — тем меньше будут различия. Бесконечный ряд отлично восстановит исходную форму за исключением, естественно, точки разрыва
vanxant
08.07.2015 15:19Если взять прямоугольное окно из двух хэвисайдов (т.е., как вы пишете, доопределить функцию нулём вне [0,T]), и f(0)!=0, f(T)!=0, то мы получим не одну точку разрыва, а две. Не знаю, откуда вы взяли про «классический» подход, но это чуть ли не худшее, что вообще можно сделать в данной ситуации.
Если уж зашла речь про оконные преобразования Фурье, то с ними вообще нужно работать очень осторожно, потому что любое окно обрезает не только сигнал, но и его спектр. Причём форма окна в спектральной области будет, скорее всего, весьма внезапной, с соответствующим геморроем для последующего анализа и особенно модификации спектра. Уж лучше сразу брать вейвлеты.
Бесконечный ряд Фурье может и «отлично» восстановит исходный сигнал, только вот работать с членами именно ряда Фурье то ещё удовольствие — что аналитически, что численно. Как ни крути, а преобразование Фурье от хэвисайда это натягивание совы на глобус, попытка аппроксимировать разрыв непрерывными функциями.
0serg
08.07.2015 15:36Если взять прямоугольное окно из двух хэвисайдов (т.е., как вы пишете, доопределить функцию нулём вне [0,T]), и f(0)!=0, f(T)!=0, то мы получим не одну точку разрыва, а две.
Верно. И?
Не знаю, откуда вы взяли про «классический» подход, но это чуть ли не худшее, что вообще можно сделать в данной ситуации.
Почему?
Если уж зашла речь про оконные преобразования Фурье, то с ними вообще нужно работать очень осторожно, потому что любое окно обрезает не только сигнал, но и его спектр
Если у Вас есть функция [0,T], то ее спектр уже обрезан (а точнее не обрезан, а искажен) и в этом виновато не окно а то что ф-я известна лишь на ограниченном итервале и без дополнительной информации восстановить, соответственно, Вы ее тоже можете лишь на этом интервале
Причём форма окна в спектральной области будет, скорее всего, весьма внезапной, с соответствующим геморроем для последующего анализа и особенно модификации спектра.
Какую хотите форму, такую и берите, в этом весь смысл использования окон. Что удобно для анализа / модификации — то и используйте.
особенно модификации спектра. Уж лучше сразу брать вейвлеты.
Смотря какой модификации. Смотря какие задачи. Преобразование Фурье не виновато в том что оно не серебрянная пуля для всех случаев жизни

0serg
08.07.2015 14:22+1Например, возьмите обратное Фурье от Фурье от {f=sin(x), x!=0; undef, x==0} (синус с выколотой точкой в нуле) — ну как, обратимо?
Оно прекрасно себе обратимо в смысле функционального анализа который рассматривает ф-и в интегральном смысле, т.е. считая, к примеру, что две ф-и отличающиеся на множестве меры ноль являются одной и той же функцией.
Ваш пример именно из этой серии.
vanxant
08.07.2015 15:29Да что вы прицепились к мере ноль. Ну давайте выколем синусу интервал от минус пи до пи. Или занулим, если вам так удобнее. Мера не ноль, но ПФ такую функцию не восстановит.

0serg
08.07.2015 15:40+1Прекрасно восстановит, с чего Вы взяли обратное? Естественно результат ПФ не-дискретной ф-и будет тоже не-дискретным и, вообще говоря, будет обобщенной ф-ей.

deniskreshikhin
08.07.2015 09:43То что вы описали не является неустойчивостью, схожий эффект присутсвует даже при элементарном суммировании чисел с плавающей запятой (см. en.wikipedia.org/wiki/Kahan_summation_algorithm) и не является проявлением неустойчивости или неоднозначности операции суммирования.
Что касается однозначности (изоморфизма) в преобразовании Фурье, то она устанавливается не для самих функций, а для алгебры их линейных преобразований.
Т.е. в мире единирогов и математиков преобразование Фурье не всегда взаимоднозначно и обратимо.
Но существует пространства где это действительно так, например пространство Шварца en.wikipedia.org/wiki/Schwartz_space

grumbler66rus
08.07.2015 08:59Вас должен был смутить тот факт, что (во всех реализациях), при преобразовании Фурье (к негармоническому сигналу) младшие члены ряда отбрасываются.

grumbler66rus
08.07.2015 09:06+1Будучи физиком по образованию, когда я увидел график «спектр мощности фликкер-шума», сразу его узнал: «Это же белый шум!».
Спасибо за тщательный разбор «феномена».
Во введении стоило указать, что «фликкер-шум» виден только в результатах преобразования Фурье и высказать гипотезу, что это погрешность преобразования.
Ну и маленький вопрос: почему же эта статья размещена не на гиктайме?
grumbler66rus
08.07.2015 09:39+1Уточнение по «виден только в результатах преобразования Фурье» — речь о форме восстановленного сигнала.
Добавлю к вопросу о форме спектра шума.
«Белый шум» по определению из Википедии (существуют и другие определения): «сигнал с равномерной спектральной плотностью на всех частотах и дисперсией, равной бесконечности». В таком определении белый шум в природе не существует, поскольку энергия (мощность) такого сигнала бесконечна (и это упомянуто в той же Википедии, там белый шум всегда ограничен некоторой полосой).
Физически осмысленный белый шум — это как раз фликкер-шум, причём на пологой горизонтальной части кривой, вырезав маленький участок, получим распределение, близкое к определению белого шума из Википедии.

0serg
08.07.2015 14:55+7Переход от (12) к (13) — это чушь которую автор побоялся обосновывать :)
Если у Вас есть n равномощных генераторов с частотами f1, f2,… fn то мощность в полосе частот от 0 до f равна Ps(f) = \sum_{i: fi<=f} P0.
Это ступенчатая функция и если уж Вам так неймётся её продифференцировать, то dPs = \sum_i P0 delta(fi) df. P0 здесь конечно можно заменить на ET(f)f, но нафига? Это все равно будет та же самая константа P0. Ваша формула (13) не получается никак.
Если смотреть предельный случай с равномерным распределением генераторов по частоте, то в силу того что Ps(f) = {число генераторов с частотой меньше f} * {мощность одного генератора}, где первое слагаемое в пределе пропорционально f, а второе является просто константой, в пределе Ps(f) = p0 * f. Отсюда со всей неизбежностью dP = p0 = const. То бишь сумма большого числа генераторов равной мощности и случайной частоты, как и ожидалось, дает белый сум
Непризнанные, блин, гении. Может все же стоит лучше проверять свои выкладки при получении «сенсационных результатов»?
TVS Автор
08.07.2015 15:27-2Здесь тоже чушь?
edu.sernam.ru/book_scin.php?id=72
0serg
08.07.2015 15:47+4Конкретизируйте вопрос. На первый взгляд там все верно. Обратите только сразу внимание на то что модель Найквиста (постоянный ЭДС случайной длительности) кардинально отличается от Вашей (равная мощность случайной частоты).

TVS Автор
08.07.2015 15:52-3Спрашиваю конкретно: переход от формулы (11.14) к формуле (11.15) указанной книги тоже чушь?

0serg
08.07.2015 15:56+4Там все ОК, но к чему Вы это спрашиваете? В Вашей формуле переход совершенно иной, обратите внимание на то что l и c в цитируемом учебнике — это константы

TVS Автор
08.07.2015 17:43Да, формула (13) и предложение перед ней неправильны.

0serg
08.07.2015 18:07+4Формула (14) и все следующие из неё выводы точно так же неверна.
В формуле (12) Вы берете мощность генератора «в точке f». Чтобы перейти от неё к «мощности в полосе частот от 0 до f» эту формулу следует просуммировать (проинтегрировать) от 0 до f. А дальнейшее дифференцирование этого интеграла как несложно догадаться просто вернет нас обратно, с оговорками на то что в не-предельном случае дискретная сумма превратится в сумму дельта-функций
TVS Автор
08.07.2015 19:53Если мощность в полосе частот определяется как интеграл P = интеграл(ET(f) * df), то мощность в полосе df равна dP = ET(f) * df, то есть получается формула (14).

0serg
08.07.2015 20:16Мощность Ps(f) в полосе частот от 0 до f равна сумма(ET(fi)*fi).
Даже если перейти к плотности то это будет интеграл(ET(f)*f*df)
TVS Автор
08.07.2015 20:23Формула «интеграл(ET(f)*f*df)» неправильна по размерности — Вт*Гц

0serg
08.07.2015 20:52+1ET(f) в сумме — это работа одного периода источника, Дж
ET(f) в интеграле — это другая величина, спектральная плотность работы одного периода, Дж/Гц
TVS Автор
08.07.2015 21:01Кажется речь шла о мощности в полосе частот, размерность которой должна быть Вт.
Дж/Гц — размерность действия, она тут причём?
0serg
08.07.2015 21:50+1Еще раз: при переходе к интегралу от суммы мы заменяем величину на ее плотность
Изначальная сумма величин выражаемых в ваттах превращается в интеграл от плотности выражаемой в Вт/Гц
Поэтому интеграл(ET(f)*f*df) имеет размерность Вт, а величина ET(f) в интеграле является «работой на единицу частоты» и измеряется в Дж/Гц.
TVS Автор
08.07.2015 22:01В статье ET(f) — имеет размерность мощности, делённой на частоту в соответствии с формулой (12) и является функцией частоты. Если я помещаю её под знак интеграла, то я должен менять её размерность?

0serg
08.07.2015 22:21+1Конечно. Интеграл функции f(t) условно говоря есть сумма f(t) * dt. Сумма f(t) и интеграл f(t) таким образом заведомо имеют разные размерности. Естественно что если Вы заменяете сумму на интеграл, то под интегралом оказывается отнюдь не исходная ф-я, а некий предел имеющий другую размерность.
Возможно более наглядное объяснение: исходная сумма есть сумма отдельных слагаемых ET(f)*f.
Каждое из этих слагаемых можно рассматривать как интеграл ET(f)*f = \int_{f-df}^{f+df} et(f)*f df над очень маленьким отрезком [f-df, f+df] при df -> 0. ET — это работа, а et — это плотность работы. Переход от суммирования к интегрированию получается объединением этих маленьких интегральчиков в интеграл над всем отрезком. А так как для отдельной точки et(f) = ET(f)/2df то наглядно видно что размерность et(f) измеряется в Дж/Гц
TVS Автор
08.07.2015 22:40Непонятно тогда, каким образом ET(f) будет связана с формулой (12), если её размерность будет Дж/Гц? Это будет уже функция не имеющая никакого отношения к данной статье.
Почему именно по частоте интегрировать? Можно по периоду, тогда размерность будет Дж/с и форма функции ET(f) будет тогда иной. То есть форма функции ET(f) будет зависеть от формулы, в которую она помещается. У меня же в статье рассматривается ET(f), которая имеет конкретную форму.
Сама модель с генераторами была введена, чтобы уйти от плотности и не привязываться к равномерному шагу по частоте.
0serg
08.07.2015 23:10+1А Вы никак не запихнете заданную в отдельных точках ET(f) в интеграл.
Я Вам же написал уже — хотите работать с ET(f) — придется брать сумму, а не интеграл.
Сумма тоже отлично дифференцируется, правда результат будет отличен от Вашего.
Для перехода же к интегралу ET(f) придется заменить на плотность et(f) — это тоже допустимый подход, но там тоже будет иной результат.
TVS Автор
08.07.2015 23:19Я рассматриваю только непрерывные функции. Для понимания статьи широкой публикой придумана модель с генераторами, под схемой расписано, что за процесс здесь рассматривается.

0serg
09.07.2015 10:19+2Давайте на уровне школьной программы, если по другому не понимаете.
Представим что Вы считаете расстояние пройденное автомобилем. Здесь 1 км проехал, здесь 500 м, здесь 2 км, здесь 4 км. Это сумма.
Представим что Вы захотели от суммы расстояний перейти к интегрированию по времени. Что уйдет под знак интеграла? Расстояние? Ничего подобного — под интеграл уйдет скорость автомобиля! И эта скорость будет пределом «пройденное расстояние / затраченное время» при время->0.
Так же и здесь. Под интеграл уходит не ET(f), а плотность et(f) по df. Что дает Ps(f) = интеграл(ef(f)*f*df) и правильную формулу 14 которая запишется как dP = p0*df, а не ту хрень что у Вас указана.
Все что из формулы 14 Вами затем выводится — это ошибка.

TVS Автор
08.07.2015 20:56Чтобы размерности совпадали, необходимо, чтобы дифференциал был безразмерным. Этому требованию удовлетворяет дифференциал логарифма частоты. Тогда интеграл в полосе частот будет равен P = интеграл(ET(f) * f * d(ln(f)), если перейти к дифференциалу по частоте, то получим P = интеграл(ET(f) * f * (df/f)), частоты в числителе и знаменателе сократятся и получим P = интеграл(ET(f) * df).

0serg
08.07.2015 21:52+3Еще раз: Вы смешиваете две разных ET(f) — «точечную», стоящую в сумме и измеряемую в джоулях и «плотность» стоящую в интеграле и измеряемую в джоулях на герц. Все банально и не требует никаких танцев с размерностью дифференциала
Откуда Вы вообще взяли логарифм? Вы что, выдумываете формулы по принципу кажущегося (ибо Вы ошиблись с размерностью ET(f)) совпадения размерности?
TVS Автор
08.07.2015 22:08Я ничего не смешиваю, у меня в статье одна единственная ET(f) с конкретной размерностью мощности, делённой на частоту.
Не понял, с чем я ошибся?
Если найти мощность в полосе частот по формуле P = интеграл(ET(f) * f * d(ln(f)), то результат будет неверным?
0serg
08.07.2015 22:22+3Вы эту формулу с логарифмом откуда взяли? Чем ее обосновываете?
Результат не просто будет неверным, он вообще у Вас такое впечатление что взят с потолка
TVS Автор
09.07.2015 00:37Я эту формулу привёл в качестве примера того, что и подынтегральная функция и результат интегрирования могут быть одной размерности.

0serg
09.07.2015 10:37При интегрировании по безразмерной величине могут, но как тезис «в качестве примера» соотносится с Вашими утверждениями из предыдущих комментариев, цитирую по списку озвученного
1. Этому требованию удовлетворяет дифференциал логарифма частоты. Тогда интеграл в полосе частот будет равен… то получим P = интеграл(ET(f) * f * (df/f))
2. Если найти мощность в полосе частот по формуле P = интеграл(ET(f) * f * d(ln(f)), то результат будет неверным?
3. Не понял, с чем я ошибся?

grumbler66rus
09.07.2015 01:05+1Суть в том, что автор статьи наглядно демонстрирует физический смысл контанты «К» в формуле спектра мощности (1).
Именно поэтому он вывел формулу (12), все части которой равны константе, получил из неё формулу (14) и уже её привёл к виду формулы 1.
0serg
09.07.2015 10:22+2Еще раз, медленно: формула 14 посчитана с грубейшей ошибкой и неверна. Правильная формула 14 выглядит так: dP = et(f)f df = p0 df где p0=const. Это тривиальный результат и из него всей остальной теории автора уже нефига не выводится

grumbler66rus
12.07.2015 10:58+1Вы правы. Я совсем забыл уже формулы интегрирования, помню только основы теории.
Автор упорно опирается на размерность, но с ней сильно путает.

ignat99
08.07.2015 18:41+3Если автор продолжит разбираться в этом вопросе, сделает моделирование, IMHO, исправит ошибки, получит новые результаты — то это будет иметь положительный эффект и для него самого и для окружающих. Лучше не останавливаться, но и исправлять ошибки, конечно. IMHO

grumbler66rus
09.07.2015 00:38Это ступенчатая функция
Ключевое тут — бесконечное количество «n».
Автор описал это аналогично тому, как в школе излагают теорию интегралов.
То бишь сумма большого числа генераторов равной мощности и случайной частоты, как и ожидалось, дает белый сум
Не понимаю, что вызвало возмущение. Автор именно что демонстрирует: шум можно представить как сумму сигналов бесконечного количества генераторов синусоидального сигнала одинаковой мощности.
0serg
09.07.2015 10:27+2Ключевое тут — бесконечное количество «n».
*устало* интегралы — это не просто бесконечное количество n. Предельный переход использованный автором фундаментально некорректен и видимо по этой причине не описан. Поскольку тут похоже представления многих людей реально ограничиваются школькой программой, то привожу школьный пример
habrahabr.ru/post/262015/#comment_8491803
Не понимаю, что вызвало возмущение. Автор именно что демонстрирует: шум можно представить как сумму сигналов бесконечного количества генераторов синусоидального сигнала одинаковой мощности.
Белый шум можно, но это не будет фликкер-шумом.

TVS Автор
09.07.2015 21:35Согласен, формула (14) некорректна. Всё переделал, результат поместил в приложение в конце статьи.

0serg
09.07.2015 22:08Я сейчас матом начну ругаться, ей-богу.
В формуле А.1 величина P(f) есть мощность в диапазоне от 0 до f.
Из этого очевидно следует что упомянутая в формуле A.1 величина ET(f) плотностью не является и являться заведомо не может
Давайте теперь пойдем с обратной стороны. Пусть спектральная плотность мощности равномерна. Как тогда выглядит функция P(f) показывающая общую мощность в полосе шириной f? Правильный ответ тривиален: P(f) = p0*f. То бишь gamma=0. Чем больше полоса — тем больше мощность. А чем же тогда является случай gamma=1? Несложно заметить что он соответствует случаю P(f)=P0 — то есть ситуации в которой общая мощность сигнала в полосе частот от 0 до f не зависит от выбора f и является некоторой константой. Давайте теперь попробуем угадать, какая же мощность приходится на произвольную полосу частот от f1 до f2? Очевидно P(f1,f2) = P(f2)-P(f1) = P0-P0 = 0. Ой. То есть случай gamma = 1 соответствует отсутствию мощности у любых частот отличных от нуля. Дальше продолжать?
Хватит пытаться доказать бредовую идею разлагая константу на два множителя (!) и дифференцируя их по частям (!!!!). Дифференциал константы — это ноль. ВСЕГДА НОЛЬ. Независимо от того на какие множители Вам взбредет его разложить.
TVS Автор
09.07.2015 22:30P(f) — зависимость мощности реализации процесса от частоты. Каждая реализация у рассматриваемого процесса состоит из одной гармоники. P(f) не привязана ни к какой полосе частот.

0serg
10.07.2015 20:08Наглядная картинка для понимания

Вы берете в качестве P(f) функцию p3(f) — «разрывность»
Но плотность — это p2(f) а получить её можно только продифференцировав p1(f) который является суммой (интегралом) мощностей от 0 до f

TVS Автор
10.07.2015 10:52Аналогия с координатой и скоростью:
— спектральная плотность мощности по частоте Sf(f) – это скорость V(t);
— мощность в полосе частот P = интеграл(Sf(f)df) – это расстояние, пройденное за интервал времени S = интеграл(V(t)dt);
— зависимость мощности от частоты P(f) – это зависимость координаты от времени x(t).
Соответственно, если найти производную зависимости координаты от времени x’(t), то получим скорость V(t), если найти производную от P(f) по частоте P’(f), то получим спектр мощности по частоте Sf(f). Можно ещё найти производную от P(f) по периоду, то получим спектр мощности по периоду.
Если следовать Вашей логике, то x(t) не существует в принципе, а есть только скорость и расстояние, пройденное за интервал времени.
Я в чём-то ошибаюсь?
0serg
10.07.2015 12:59Аналогия с координатой и скоростью:
Аналогия совершенно верная
зависимость мощности от частоты P(f) – это зависимость координаты от времени x(t).
Просто зависимость координаты x(t) от времени (считая скорость неотрицательной) есть пройденный путь за время 0...t. Если мы, к примеру, прошли в момент t1 путь l1, затем в t2 l2, затем в t3 l3 и t1<t2<t3<t то x(t)=l1+l2+l3.
Так же и с мощностью — то что Вы дифференцируете должно быть суммой мощностей приходящихся на диапазон 0...f.
Давайте попробуем вернуться к азам теории интегрирования и дифференцирования. Возьмем три функции, которые я назову для простоты p1, p2 и p3
* p1(f) = первообразная, общая мощность приходящаяся на диапазон частот [0,f]
* p2(f) = dp1/df = lim_{df->0} (p1(f+df)-p1(f))/df — спектральная плотность мощности для частоты f
* p3(f) = p1(f+0)-p1(f-0) = lim_{df->0} (p1(f+df)-p1(f-df)) — мощность в частоте f
Это три разные функции — интеграл по мощности, плотность мощности, и ф-я показывающая «величину разрыва» интеграла по мощности в точке. Обратите внимание что заведомо p3 != p1 и p3 != p2.
Так вот, в Вашей исходной модели с генераторами P(f) — это p3(f), величина разрыва. Это не плотность и не первообразная. Вы же на разные лады пытаетесь подменить p3(f) на p1(f) и перейти к p2(f), что приведет к домножению p1 на 1/f и даст желаемый Вами «фликкер-шум». Так вот, такую подмену делать нельзя. p1(f) можно представить только в виде суммы из p3(f), но там ничего хорошего, как я Вам давным-давно написал, не получается.
TVS Автор
10.07.2015 14:28Зависимость координаты x(t) от времени – это координата точки в момент времени t. Если в момент времени 0 координата x(0) = 1, а в момент времени t, координата не изменилась x(t) = 1, то пройденный путь равен 1? Чтобы найти пройденный путь по x(t) необходимо использовать формулу длины кривой:
ru.wikipedia.org/wiki/%D0%94%D0%BB%D0%B8%D0%BD%D0%B0_%D0%BA%D1%80%D0%B8%D0%B2%D0%BE%D0%B9
Спектральная плотность мощности показывает скорость изменения мощности в точке f. Если эта скорость не равна нулю, то мощность сигнала в точке f будет отличаться от мощности в точке f+df. Соответственно, если спектральная плотность мощности отлична от нуля и равна константе, то это свидетельствует о росте мощности с увеличением частоты.
0serg
10.07.2015 14:36Соответственно, если спектральная плотность мощности отлична от нуля и равна константе, то это свидетельствует о росте мощности с увеличением частоты.
Все верно, если p2(f)=const то это свидетельствует о росте мощности с увеличением частоты.
Но Вы-то утверждаете что p1(f)=const, а в этом случае p2(f) = 0
Случай же p2(f)=const соответствует p1(f)=p0*f
TVS Автор
10.07.2015 15:33Вы рассматриваете p1(f) как определённый интеграл в полосе частот от 0 до f.
Это всё равно, что рассматривать интеграл от скорости за время от 0 до t. Такой интеграл даст путь, пройденный за время t. Если брать неопределённый интеграл, то в точке t он будет равен координате, из которой вычтена константа. Можно и так сказать – производная от x(t) даёт функцию скорости V(t), соответственно неопределённый интеграл от скорости даёт зависимость положения от времени с вычтенной константой.
Если перейти к спектрам, то неопределённый интеграл от спектральной плотности мощности будет равен зависимости мощности от частоты и никакого отношения к какой-либо полосе частот она не будет иметь. Проблема в том, что такая зависимость никем никогда не применялась, хотя бы потому, что непонятен её физический смысл. Чтобы придать ей смысл, я и придумал процесс, каждая реализация которого состоит только из одной гармоники.
Если сигнал обладает равномерным спектром, то его производная (хоть по частоте, хоть по периоду) должна быть равна нулю. Этой производной как раз и является спектральная плотность мощности.
0serg
10.07.2015 18:23Если перейти к спектрам, то неопределённый интеграл от спектральной плотности мощности
Поэтому я и не хочу брать неопределенный интеграл, а предпочитаю конкретную его реализацию определенную соотношением p1(0)=0.
никакого отношения к какой-либо полосе частот она не будет иметь
При указанном мною выборе реализации неопределенного интеграла это будет мощность в полосе частот от 0 до f. Вы вправе выбрать другую реализацию, но я не вижу причин не использовать именно эту — она равносильна любой другой и удобна в интерпретации
Проблема в том, что такая зависимость никем никогда не применялась, хотя бы потому, что непонятен её физический смысл
Я Вам уже раза четыре наверное сказал про физический смысл и он тривиален — мощность в полосе частот от 0 до f
Чтобы придать ей смысл, я и придумал процесс, каждая реализация которого состоит только из одной гармоники.
Еще раз, медленно, p1 != p3. Это черт возьми две совершенно разных вещи, хотя и с одинаковой размерностью
Если сигнал обладает равномерным спектром, то его производная (хоть по частоте, хоть по периоду) должна быть равна нулю
Производная чего? Спектра? Что является спектром? Обычно вообще-то спектром называют спектральную плотность p2(f) и «равномерный спектр» соответствует p2(f)=const.
Этой производной как раз и является спектральная плотность мощности.
Спектральная плотность мощности является производной кумулятивной ф-и распределения (первообразной) и последняя может быть константой только в случае если спектральная плотность мощности тождественно равна 0.
TVS Автор
10.07.2015 20:09Поэтому я и не хочу брать неопределенный интеграл, а предпочитаю конкретную его реализацию определенную соотношением p1(0)=0.
Вы вправе не хотеть, на мою статью это не влияет.
При указанном мною выборе реализации неопределенного интеграла это будет мощность в полосе частот от 0 до f. Вы вправе выбрать другую реализацию, но я не вижу причин не использовать именно эту — она равносильна любой другой и удобна в интерпретации
Причину я много раз говорил — нужно уйти от мощности в полосе частот.
Я Вам уже раза четыре наверное сказал про физический смысл и он тривиален — мощность в полосе частот от 0 до f
Я Вам в который раз говорю, что неопределённый интеграл — это не мощность полосы от 0 до f.
Еще раз, медленно, p1 != p3. Это черт возьми две совершенно разных вещи, хотя и с одинаковой размерностью
У Вас p1(f) — это определённый интеграл, естественно, он не равен p3(f). Если p1(f) — неопределённый интеграл, то он будет являться мощностью реализации процесса с частотой f. Я, вроде, и аналогию с координатой точки привел, как ещё объяснять?
Производная чего? Спектра? Что является спектром? Обычно вообще-то спектром называют спектральную плотность p2(f) и «равномерный спектр» соответствует p2(f)=const.
Это уже хороший вопрос! Сигналом с равномерным спектром по определению является сигнал с равномерной спектральной плотностью мощности, то есть сигнал, у которого на одинаковые полосы частот приходятся одинаковые мощности. У меня и возник вопрос, почему сигнал с равномерной спектральной плотностью мощности по частоте является равномерным, если с тем же успехом можно по определению приравнять броуновский шум к сигналам с равномерным спектром, так как его спектральная плотность мощности по периоду равномерна. У частоты над периодом есть какое-то преимущество? Все привыкли использовать только равномерный шаг по частоте, так как он используется в преобразовании Фурье и все свои рассуждения привязывают к полосе частот.
Используя неопределённый интеграл, я ухожу от полос частот и получаю в итоге, что сигнал с равномерным спектром не является равномерным ни по частоте, ни по периоду, а по некоторой «средней» спектральной координате — натуральному логарифму частоты, который, кстати, равен по модулю натуральному логарифму периода.
Спектральная плотность мощности является производной кумулятивной ф-и распределения (первообразной) и последняя может быть константой только в случае если спектральная плотность мощности тождественно равна 0.
Причём здесь функция распределения?
0serg
10.07.2015 20:34У Вас p1(f) — это определённый интеграл, естественно, он не равен p3(f). Если p1(f) — неопределённый интеграл, то он будет являться мощностью реализации процесса с частотой f.
Послушайте, хватит фигней страдать. Неопределенный интеграл — это семейство функций вида f(x)+c где c — произвольная константа. У неопределенного интеграла НЕ БЫВАЕТ ВЫЧИСЛИМОГО ЗНАЧЕНИЯ В ТОЧКЕ. Потому что это СЕМЕЙСТВО ФУНКЦИЙ, блин. Потому он и НЕОПРЕДЕЛЕННЫЙ.
Вычислить же можно только определенный интеграл. Например последовав моему предложению.
Я, вроде, и аналогию с координатой точки привел, как ещё объяснять?
Ваша аналогия с координатой верна — напомню:
«соответственно неопределённый интеграл от скорости даёт зависимость положения от времени с вычтенной константой.»
Только, блин, чему равна эта константа? Ау? И понимаете ли вы что фиксирование этой константы определенным образом превращает неопределенный интеграл в определенный?
Это уже хороший вопрос! Сигналом с равномерным спектром по определению является сигнал с равномерной спектральной плотностью мощности
Но Вы я так понимаю используете другое определение :D?
У частоты над периодом есть какое-то преимущество?
С частотой работать удобнее. Но вообще Вы страдаете здесь хренью, потому как задаетесь вопросом «почему сигнал спектральная плотность мощности которого равна константой называют сигналом с равномерным спектром». Да вот потому что назвали его так. Хоть картошкой могли бы назвать, хоть кактусом, название — это просто ярлычок привязанный к строго конкретному виду сигналов и единственная функция этого ярлычка — дать двум разным людям понять о чем конкретно идет речь. Вы же пытаетесь здесь прилепить ярлычок от одного процесса к заведомо другому потому что Вам так больше нравится. У Вас могут быть причины считать что так будет лучше, но подобный подход фундаментально противоречит назначению ярлычка — давать возможность разным людям понимать друг друга.
Используя неопределённый интеграл, я ухожу от полос частот и получаю в итоге, что сигнал с равномерным спектром не является равномерным ни по частоте, ни по периоду
Под «сигналом с равномерным спектром» здесь понимается «предел сигнала получаемого сложением N сигналов от генераторов со случайной частотой и одинаковой мощностью при N->inf». Так вот, еще раз, медленно и по буквам: предел этого сигнала имеет равномерный спектр по частоте — см. картинку:

Вы же берете p3(f), выдаете за p1(f) (!), дифференцируете ее (!!!) и получившийся результат выдаете за p2(f)
TVS Автор
11.07.2015 12:37Что мешает просто взять и сопоставить спектральной плотности мощности некоторую непрерывную зависимость мощности от частоты P(f) (прошу заметить, что это не мощность в полосе от 0 до f, а именно зависимость мощности от частоты), производная от которой будет равна спектральной плотности мощности?
Если функция p1(f) в полосе частот от 0 до f равна const != 0 в каждой точке, то спектральная плотность мощности будет всюду равна нулю, при этом мощность самого сигнала будет равна const, которая может быть какой угодно, хоть бесконечной. Что это за сигнал такой, что обладает ненулевой мощностью и при этом его СПМ всюду равна нулю? Никакой ступеньки в нуле нет, поэтому нельзя сказать, что СПМ будет иметь дельта-функцию в нуле.
Можно обойтись без слов типа «фигней страдать», «Ау» и прочее, неприятно такое читать!
0serg
12.07.2015 21:201. Любой определенный интеграл спектральной плотности p2(f) является суммой мощностей в соответствующем диапазоне частот. (тривиальные основы интегрального исчисления, заставляющие меня эмоционально выражаться насчет фигни)
2. (менее тривиально, функциональный анализ) Допустим что Вы взяли функцию p3(f) которая «просто равна мощности в точке f». Эта функция хорошо определена для конечной суммы источников сигнала. Возникает однако вопрос: если f не является ни одной из ранее выбранных частот, то чему равно p3(f)? Очевидно нулю (см. график выше). Но тогда p3(f)=0 почти всюду и более того, p3(f)=0 в любом из функциональных пространств. Поэтому при n->inf ф-я p3(f) сходится к нулю почти всюду и не может превратиться в ф-ю вида p3(f)=c
3. Если мы не собираемся оперировать отрицательными частотами, то все p1(f)=p2(f)=p3(f)=0 для любого f<0. Это естественно подразумевает ступеньку в нуле для p1(f) и дельта-функцию для p2(f)
TVS Автор
13.07.2015 23:12Следует различать СПМ процесса и СПМ реализации процесса. Я рассматриваю процесс с непрерывным спектром, однако каждая реализация этого процесса обладает дискретным спектром, состоящим только из одной гармоники. Ближайший распространённый аналог – процесс, каждая реализация которого состоит из гармонического сигнала со случайной начальной фазой.
P(0 Гц) – мощность реализации с частотой 0 Гц, P(10 Гц) – мощность реализации с частотой 10 Гц и так далее. P(f) – мощность реализации процесса с частотой f, при этом сама P(f) является непрерывной функцией, так как мною изначально задано, что частота может принимать любое значение от нуля до бесконечности.
Спектральную плотность мощности неэргодического случайного процесса определяют усреднением по СПМ множества реализаций. Если рассмотреть мощность моего процесса в полосе частот от 0 до конечной f, то она будет равна средней мощности данной полосы всех реализаций, то есть равна нулю, так как в полосу частот от 0 до f попадает в бесконечное число раз меньшее количество гармоник, чем в полосу от f до бесконечности. Мощность в полосе частот от 0 до бесконечности равна P0, так как в этот диапазон частот попадают все реализации (мощность каждой реализации равна P0). Получается, что p1(f) рассматриваемого процесса равна нулю всюду, но имеет ступеньку на бесконечной частоте. Соответственно СПМ такого процесса также всюду равна нулю и обладает дельта-функцией на бесконечной частоте. Таким образом, рассматриваемый мною процесс обладает Sf(f) = 0, при этом его мощность равна P0.
Вы же думаете, что я рассматриваю сигнал, содержащий бесконечное число гармоник на всех частотах. Такой сигнал обладает либо бесконечной мощностью в любой полосе частот, либо все его гармоники должны обладать нулевой амплитудой.
0serg
14.07.2015 01:32Уважаемый TVS, начнем с того что общеизвестно что белый шум имеет бесконечно большую мощность. Физически такого процесса не бывает, это просто математическое приближение которое аппроксимирует реальный шум. Дабы сразу пресечь попытки закричать «вы тут какую-то хрень изобрели, а мой шум физичен», замечу что мощность фликкер-шума точно так же бесконечна, а прекрасным сколь угодно близким физическим приближением белого шума является шум с равномерной спектральной плотностью в диапазоне [0,f] для достаточно большого f, равный нулю вне этого спектрального диапазона (для фликкер-шума подобное приближение, кстати, построить сложнее). К той же серии относится наблюдение что стационарные процессы вообще не физичны (любой стационарный процесс конечной мощности утилизирует бесконечно большую энергию :))
Перейдем, однако, к Вашей модели. Давайте попробуем для начала прикинуть каково будет распределение плотности вероятности встретить встретить процесс с моночастотой f? Но внезапно такой простой вопрос остается без ответа, поскольку распределение-то это должно быть равномерным по f, а интеграл от плотности по всем возможным частотам должен давать единицу. То есть плотность вероятности p(f) встретить частоту f, очевидно, в рамках озвучивавшейся Вами логики, тождественно равна нулю всюду, но интеграл по этой плотности «на бесконечности» дает единицу :). В этом месте Вам по идее должно бы начать приходить в голову что наблюдаемые странные проблемы со «спектральной мощностью» как-то связаны с тем что у используемого процесса есть некоторые проблемы с определением плотности вероятности по частоте :)
Едем однако дальше. Вторая бросающаяся в глаза странность состоит в том, что Ваш подход подразумевает что любое реальное измерение подобного шума должно будет показывать именно синусоиду, поскольку измерение случайного процесса должно давать одну из его реализаций. Но давайте попробуем выкрутиться и рассмотрим, скажем случайный процесс получающийся разбиением временной оси на случайные интервалы времени и взятием на каждом из этих интервалов своей собственной реализации описанного моносинусоидального процесса. Эдакий моногенератор фиксированной мощности с плавающей частотой скачкообразно меняющейся случайным образом в случайные моменты времени. Будет правда не совсем понятно почему именно подобная штука должна что-то хорошо аппроксимировать, но допустим на минуту что какая-то физическая модель хорошо описывается именно таким образом.
Попробуем теперь все-таки вычислить спектр нашего процесса. Первое наблюдение которое бросается в глаза состоит в том что нам неизвестны ни спектральная плотность p(f) процесса, ни плотность вероятности по частоте, ни первообразная по частоте. Почему Вы решили что можно взять не являющуюся даже вероятностью функцию P(f) и использовать её в качестве первообразной, дифференцирование которой даст спектральную мощность лично для меня — загадка. Как Вы верно заметили, наивный подход к усреднению просто приведет к плотности вероятности по частоте тождественно равной нулю и, следовательно, такому же тождественно нулевому спектру мощности.
Я опущу более строгое доказательство, но можно строго прийти к точно такому же результату рассматривая указанную модель со случайной ступенчатой перестройкой по частоте как предел некоторой последовательности конечных сигналов. Идея там вращается вокруг того что мощность любого сигнала конечной длительности в пределе оказывается равной нулю, а в рамках выбранной модели спектральные пики для отдельных частот перекрываться практически не будут.
TVS Автор
20.07.2015 19:36В конце статьи я добавил ещё одно приложение, интересно услышать Ваше мнение.

0serg
28.07.2015 09:00Построение остроумное, но не полное (технически если следовать описанию то будет лишь одна гармоника — f=T=1) к реальному шуму не имеющее никакого отношения — Вы просто неким произвольным образом выбрасываете гармоники.

TVS Автор
03.08.2015 19:50но не полное
Более подробно в приложении В.
0serg
04.08.2015 23:09Возьмем непрерывное преобразование Фурье C(f) = \int_{-\inf}^{+\inf}s(t)exp(-j*ft)dt (здесь еще надо домножить на константу, ну не суть важно).
Доопределим теперь s1(t) = s(t) * I(t) где I(t) — это интервальная функция, равная 1 на (-T/2,T/2) и нулю вне этого интервала. C(s1)(f) = \int_{-T/2}^{+T/2}s(t)exp(-j*ft)dt — у такой функции интеграл уже определен на конечном отрезке
Наконец указанные Вами коэффициенты ряда Фурье Ck = C(k*w0), k=0,1,....- просто значения этой функции C(s1) в наборе равномерно распределенных точек
Почему вообще вычисляют Ck? Дело в том что для T-периодической функции s, C(s)(f) = C(s1)(f)*delta(x-f) для f=k*w0 и C(s)(f)=0 для всех остальных f. То есть спектр f состоит из набора дельта-функций стоящих с шагом k*w0 и этот спектр можно посчитать через подсчет C(s1) с интегрированием на конечном отрезке. Или что то же самое, f представима в виде суммы (ряда) Фурье с коэффициентами Ck.
Идея откуда и зачем возникают коэффициенты Ck понятна? Заметьте что шаг по частоте в выбранном спектре не случаен и тесно завязан на то что функция является T-периодической. В общем случае если периодичность не гарантирована интеграл придется брать на (-\inf,+inf). Коэффициенты Ck там впрочем тоже представляют интерес, но уже в силу теоремы Найквиста. Но там тоже нужна специальная функция (с ограниченным спектром), а метод восстановления оригинала по Ck совершенно иной — никакого ряда с коэффициентами Ck там уже не возникает
Едем теперь к Вашему примеру с дельта-функцией. И сходу замечаем два тривиальных соображения — дельта-функция не является ни периодической, ни обладает ограниченным спектром. Хотя при этом конечно C(delta)(f)=1 и C(delta * I)(f) = 1, так что формальный подсчет Ck даст для любого k единицу (константу). Но вот только, увы, ряд Фурье с этими коэффициентами \sum_k 1 * exp(-jwk) к дельта-функции, увы, не сойдется. Облом номер один
Далее пытаемся перейти к пределу с непрерывным спектром. Но здесь нас ждет облом номер два — у T-периодической функции спектр сосредоточен в точках с частотой k/T где k — целое число и это k/T ну никак, странным образом, на произвольную частоту f странным образом не обобщается. Шаг между соседними частотами строго равен 1/T где T-это период функции. Как Вы предлагаете от разрывного спектра лежащего на сетке со строго определенным шагом жестко заданным периодом функции перейти к непрерывному?
Далее делается еще более забавная вещь. Вместо того чтобы считать C(k*w0) Вы начинаете считать C(w0/k). Ну ок, Вы посчитаете C(f) в странно выбранном наборе точек, и что дальше? Это все равно будет спектр по частоте, просто посчитанный не в точках вида k*w0 а в точках вида w0/k. И естественно этот спектр отличается от «спектра по периоду», да :).
Дальше Вы довольно разумным образом рассуждаете про дискретные периодические функции, а затем… применяете эти выкладки к дельта-функции. Но, простите, дельта-функция НЕ является периодической. Вообще. Вот гребенка Дирака будет периодической, но вот только спектр гребенки Дирака уже не является константой как у одиночной дельта-функции :)
Далее там идет попытка все же взять гребенку Дирака, и сказать что
а) ее спектр состоит лишь из частот w0*k
б) соответствующие периоды это 1/(w0*k)
в) но гребенка Дирака периодична только с периодами вида k/w0
г) значит валидны только такие k для которых 1/(w0*k1) == k2/w0 для каких-то k1, k2.
Здесь однако Вы, как я уже сказал, упускаете то небольшое обстоятельство что w0 тут как ни крути сокращается и следовательно единственно возможные k1=k2=1 и стало быть гребенка Дирака — это то же что обычная синусоида :). Шутка. В реальности, как наверное Вы уже догадываетесь, эта логика не работает и причина тому довольно банальна: наличие в спектре функции частоты f не делает функцию 1/f-периодической и наоборот, у T-периодической функции может отсутствовать в спектре частота 1/T. К примеру функция sin(2x)+sin(3x) является 2pi-периодической, но не имеет в своем спектре частотной гармоники 1/2pi, зато имеет гармонику 3/2pi, хотя 2pi/3-периодической не является. Другими словами из б) и в) никак не следует г).
Утомился я с Вами, извините. Это неплохая разминка для ума, но она начала мне слегка надоедать в силу того что отнимает приличное количество времени
TVS Автор
05.08.2015 12:18Чтобы Вас сильно не утомлять, я прокомментирую только самый важный пункт Вашего ответа.
Дальше Вы довольно разумным образом рассуждаете про дискретные периодические функции
Фактически, Вы соглашаетесь с тем, что периодический дискретный во временной области сигнал обладает логарифмической сеткой частот:
— Спектр периодического сигнала определён только в точках
fn = ?f * n, где n – целое число, ?f – частотный шаг.
— Спектр дискретного сигнала определён только в точках
fm = (1 / Tm) = (1 / (?t * m)), где m – целое число, ?t – шаг дискретизации.
— Спектр дискретного периодического сигнала определён только в точках fn == fm или (?f * n) == 1 / (?t * m).
Если ?f = 1, ?t = 1, то n = 1; m = 1.
Если ?f = 0,5, ?t = 0,5, то n = 1, 2, 4; m = 4, 2, 1.
Если ?f = 0,25, ?t = 0,25, то n = 1, 2, 4, 8, 16; m = 16, 8, 4, 2, 1.
Если ?f -> 0, ?t -> 0, то n и m принимают бесконечное число значений с равномерным логарифмическим шагом:
n = (2 ^ x), где x = 0, 1, 2, 3,… inf,
m = (2 ^ y), где y = inf, … 3, 2, 1, 0.
Устремляя ?f и ?t к нулю, мы переходим от дискретного периодического сигнала к непрерывному непериодическому сигналу, при этом частотный шаг остаётся логарифмическим.
0serg
05.08.2015 23:23Фактически, Вы соглашаетесь с тем, что периодический дискретный во временной области сигнал обладает логарифмической сеткой частот:
Любой периодический во временной области сигнал обладает сеткой частот вида k/T где T — это период. Значения вне этой сетки равны нулю, на сетке _могут_ быть не-нулевыми. Что такое «логарифмическая сетка частот»?
?f – частотный шаг.
Неверно. ?f = 1/T где T — это период. Причем это соотношение не говорит что в значениях частоты k?f что-то будет для всех k, только что _вне_ этих частот точно ничего не будет. Поэтому хотя T конечно можно домножать на любую константу, «устремляя ?f к нулю», но смысла в этом никакого — ненулевые значения все равно определяются максимально жесткой сеткой, а она соответствует минимально возможному T.
Спектр дискретного сигнала определён только в точках
fm = (1 / Tm) = (1 / (?t * m)), где m – целое число, ?t – шаг дискретизации
Это абсолютно неверный тезис. Дискретный сигнал может (и обычно будет) обладать непрерывным спектром. Дискретный периодический сигнал как и любой периодический будет иметь дискретный спектр, да, но шаг между не-нулевыми значениями в этом спектре будет определен периодом функции T и «устремить его к нулю» не удастся

Jecky
08.07.2015 16:08+1Да, это известный артефакт преобразования Фурье — высокочастотный сигнал, там где его нет. Разбирается в курсе обработки сигналов. Собственно, загадкой, насколько я понимаю, никогда не был для тех, кто внимательно слушал курс.

dtestyk
08.07.2015 22:20Согласен, розовый шум — самый интересный. Цитата отсюда:
Voss [3], Hennig [4], and Levitin [5] have shown that in
many musical pieces, from classical to rock music, the
fluctuation of pitch (frequency), loudness and duration
obeys 1/f power law. The exponent ? ranges from 0.4
to 1.4, depending on the composer and genre. The range
of ? suggests that human music keeps a balance between
predictability (? = 2) and randomness (? = 0). The 1/f
relation is also observed in several natural phenomena,
such as the frequency of earthquakes and the fluctuation
of heart beat rate.

sci_nov
09.07.2015 07:54+2Вывод: фликкер-шум — сигнал с равномерным спектром, спектр которого искажается преобразованием Фурье.
Странно… А к чему тогда отнести сигнал с выхода датчика случайных нормальных чисел, например, в той же Octave randn(128,1)? Измерение спектральной плотности мощности с помощью БПФ и усреднения квадрата модуля спектра даёт более менее ровный спектр (разве что возле нулевой и первой гармоники есть небольшой артефакт, но это объяснимо, так как длина реализации ограничена 128 отсчётами).


kbtsiberkin
09.07.2015 15:57+1По материалу поддерживаю комментаторов — смоделировать всё-таки нужно систему и посмотреть, что там будет.
Вот, кстати, не далее как в свежайшем номере УФН очередная статья о фликкер-шуме вышла. Пробуют получить через законы механики и описание случайных блужданий в системе множества частиц. Вполне интересно.
vladob
12.07.2015 01:17Не знаю-не знаю.
Может я и не уловил драматизм ситуации.
Еще в конце 70-х, когда я впервые услышал про фликкер-шум со спектром 1/f в универовском спецкурсе ядерно-физических измерений, это явление объяснялось, как наблюдение флуктуаций, вследствие теплового «броуновского» движения (кажется в стохастике это называется «винеровский процесс»), через полосовой фильтр, коим является по сути любая регистрирующая система (цифровая или аналоговая — не важно).
Вот здесь много и подробно описан, так что при всем моем «спасибо» автору за статью, ощущения открытия от прочтения не случилось.
deniskreshikhin
13.07.2015 01:44+2Драматизм заключается в том, что изначально под фликкер шумом подразумевались нестационарные процессы в электроламповых приборах связанный с флуктуацией эмиссии электронов с катода (мерцающий шум). Это отличает шум от броуновского, т.к. броуновский стационарен — имеет медленно изменяющиеся дисперсию и спектр. Наоборот дисперсия фликкер-шума постоянно меняется, а понятие спектра вообще неприменимо к нестационарным процессам. В этом и есть драматизм ситуации.
Но т.к. в технике в основном используются линейные стационарные модели случайных процессов (которые развили Винер, Хинчин и Колмогоров), то фликкер шум стали учитывать как стационарный 1/f шум.
Но это абсолютно не значит что этот шум стационарен. Точно так же тепловой шум имеет совсем не бесконечный спектр, но в технических моделях это пренебрежение допустимо, главное что бы это не искажало конечный результат.

ignat99
14.07.2015 14:35Это записи серии измерений фликкер шума (?) в контексте работ Козырева. Может кто-то захочет повторить опыты или прочитает и сбережёт своё личное время не повторяя чужих ошибок.


Fil
Теплый ламповый BMP :)
tegArt
Неизменное качество с 1986 года, не имеющее конкурентов и по сей день. )