
Пару слов о методе
Для того чтобы не расписывать много теории с математическими терминами и определениями, предлагаю рассмотреть пару вариантов построения задачи о назначениях, и я думаю Вы сразу поймете в каких случаях применим Венгерский метод:
- Задача о назначении работников на должности. Необходимо распределить работников на должности так, чтобы достигалась максимальная эффективность, или были минимальные затраты на работу.
- Назначение машин на производственные секции. Распределение машин так, чтобы при их работе производство было максимально прибыльным, или затраты на их содержание минимальны.
- Выбор кандидатов на разные вакансии по оценкам. Этот пример разберем ниже.
Как Вы видите, вариантов для которых применим Венгерский метод много, при этом подобные задачи возникают во многих сферах деятельности.
В итоге задача должна быть решена так, чтобы один исполнитель (человек, машина, орудие, …) мог выполнять только одну работу, и каждая работа выполнялась только одним исполнителем.
Необходимое и достаточное условие решения задачи – это ее закрытый тип. Т.е. когда количество исполнителей = количеству работ (N=M). Если же это условие не выполняется, то можно добавить вымышленных исполнителей, или вымышленные работы, для которых значения в матрице будут нулевыми. На решение задачи это никак не повлияет, лишь придаст ей тот необходимый закрытый тип.
Step-by-step алгоритм на примере
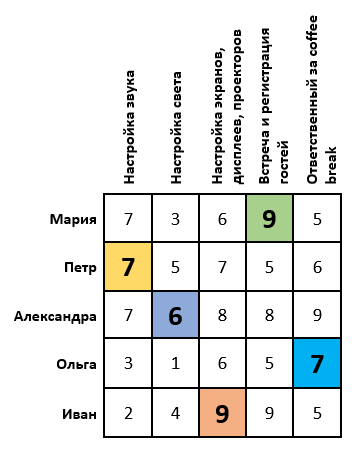
Постановка задачи: Пусть намечается важная научная конференция. Для ее проведения необходимо настроить звук, свет, изображения, зарегистрировать гостей и подготовиться к перерывам между выступлениями. Для этой задачи есть 5 организаторов. Каждый из них имеет определенные оценки выполнения той, или иной работы (предположим, что эти оценки выставлены как среднее арифметическое по отзывам их сотрудников). Необходимо распределить организаторов так, чтобы суммарная их оценка была максимальной. Задача имеет следующий вид:
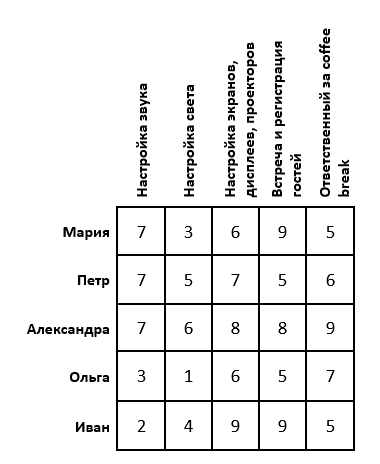
Если задача решается на максимум (как в нашем случае), то в каждой строке матрицы необходимо найти максимальный элемент, его же вычесть из каждого элемента соответствующей строки и умножить всю матрицу на -1. Если задача решается на минимум, то этот шаг необходимо пропустить.
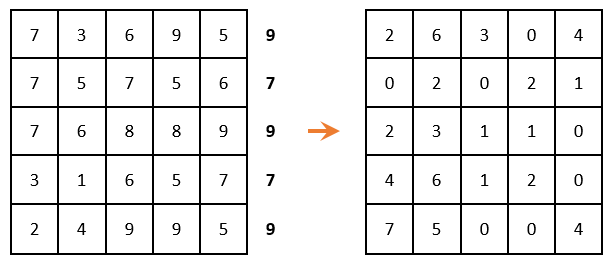
В каждой строке и в каждом столбце должен быть только один выбранный ноль. (т.е. когда выбрали ноль, то остальные нули в этой строке или в этом столбце уже не берем в расчет). В этом случае это сделать невозможно:
(Если задача решается на минимум, то необходимо начинать с этого шага). Продолжаем решение далее. Редукция матрицы по строкам (ищем минимальный элемент в каждой строке и вычитаем его из каждого элемента соответственно):

Т.к. все минимальные элементы – нулевые, то матрица не изменилась. Проводим редукцию по столбцам:
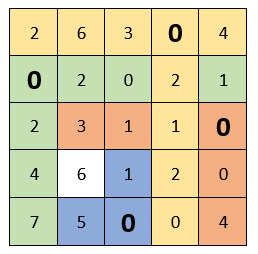
Опять же смотрим чтобы в каждом столбце и в каждой строке был только один выбранный ноль. Как видно ниже, в данном случае это сделать невозможно. Представил два варианта как можно выбрать нули, но ни один из них не дал нужный результат:
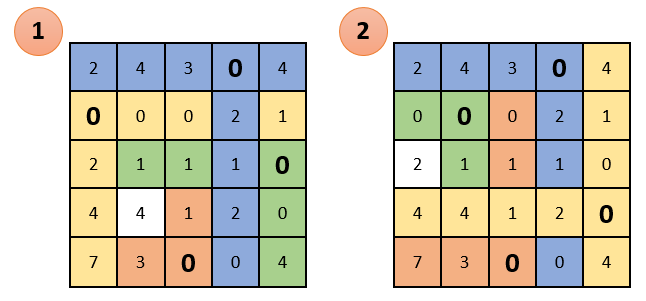
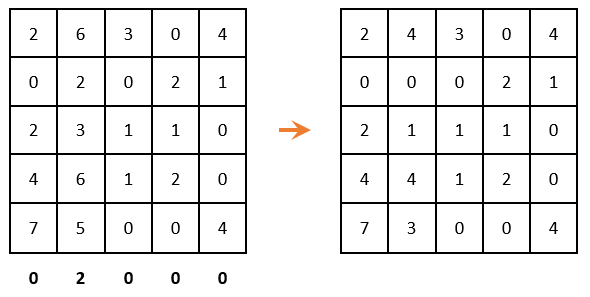
Продолжаем решение дальше. Вычеркиваем строки и столбцы, которые содержат нулевые элементы (ВАЖНО! Количество вычеркиваний должно быть минимальным). Среди оставшихся элементов ищем минимальный, вычитаем его из оставшихся элементов (которые не зачеркнуты) и прибавляем к элементам, которые расположены на пересечении вычеркнутых строк и столбцов (то, что отмечено зеленым – там вычитаем; то, что отмечено золотистым – там суммируем; то, что не закрашено – не трогаем):
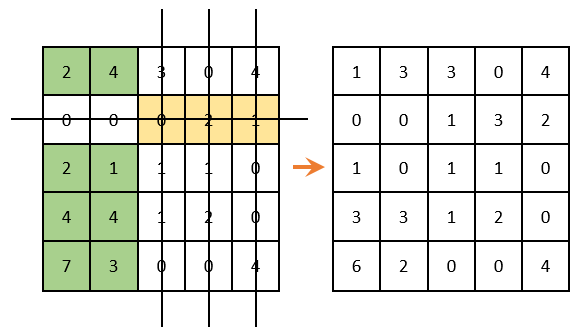
Как теперь видно, в каждом столбце и строке есть только один выбранный ноль. Решение задачи завершаем!
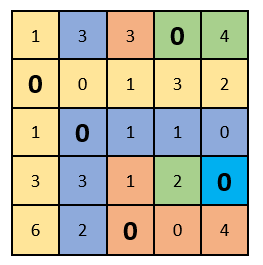
Подставляем в начальную таблицу месторасположения выбранных нулей. Таким образом мы получаем оптимум, или оптимальный план, при котором организаторы распределены по работам и сумма оценок получилась максимальной:
Если же вы решаете задачу и у вас до сих пор невозможно выбрать нули так, чтобы в каждом столбце и строке был только один, тогда повторяем алгоритм с того места где проводилась редукция по строкам (минимальный элемент в каждой строке).
Реализация на языке программирования R
Венгерский алгоритм реализовал с помощью рекурсий. Буду надеяться что мой код не будет вызывать трудностей. Для начала необходимо скомпилировать три функции, а затем начинать расчеты.
Данные для решения задачи берутся из файла example.csv который имеет вид:

#Подключаем библиотеку для удобства расчетов
library(dplyr)
#Считываем csv фаил (первый столбик - названия строк; первая строка - названия столбцов)
table <- read.csv("example.csv",header=TRUE,row.names=1,sep=";")
#Проводим расчеты
unique_index <- hungarian_algorithm(table,T)
#Выводим
cat(paste(row.names(table[as.vector(unique_index$row),])," - ",names(table[as.vector(unique_index$col)])),sep = "\n")
#Считаем оптимальный план
cat("Оптимальное значение -",sum(mapply(function(i, j) table[i, j], unique_index$row, unique_index$col, SIMPLIFY = TRUE)))
#____________________Алгоритм венгерского метода__________________________________
hungarian_algorithm <- function(data,optim=F){
#Если optim = T, то будет искаться максимальное оптимальное значение
if(optim==T)
{
data <- data %>%
apply(1,function(x) (x-max(x))*(-1)) %>%
t() %>%
as.data.frame()
optim <- F
}
#Редукция матрицы по строкам
data <- data %>%
apply(1,function(x) x-min(x)) %>%
t() %>%
as.data.frame()
#Нахождение индексов всех нулей
zero_index <- which(data==0, arr.ind = T)
#Нахождение всех "неповторяющихся" нулей слева-направо
unique_index <- from_the_beginning(zero_index)
#Если количество "неповторяющихся" нулей не равняется количеству строк в исходной таблице, то..
if(nrow(unique_index)!=nrow(data))
#..Ищем "неповторяющиеся" нули справа-налево
unique_index <- from_the_end(zero_index)
#Если все еще не равняется, то продолжаем алгоритм дальше
if(nrow(unique_index)!=nrow(data))
{
#Редукция матрицы по столбцам
data <- data %>%
apply(2,function(x) x-min(x)) %>%
as.data.frame()
zero_index <- which(data==0, arr.ind = T)
unique_index <- from_the_beginning(zero_index)
if(nrow(unique_index)!=nrow(data))
unique_index <- from_the_end(zero_index)
if(nrow(unique_index)!=nrow(data))
{
#"Вычеркиваем" строки и столбцы которые содержат нулевые элементы (ВАЖНО! количество вычеркиваний должно быть минимальным)
index <- which(apply(data,1,function(x) length(x[x==0])>1))
index2 <- which(apply(data[-index,],2,function(x) length(x[x==0])>0))
#Среди оставшихся элементов ищем минимальный
min_from_table <- min(data[-index,-index2])
#Вычитаем минимальный из оставшихся элементов
data[-index,-index2] <- data[-index,-index2]-min_from_table
#Прибавляем к элементам, расположенным на пересечении вычеркнутых строк и столбцов
data[index,index2] <- data[index,index2]+min_from_table
zero_index <- which(data==0, arr.ind = T)
unique_index <- from_the_beginning(zero_index)
if(nrow(unique_index)!=nrow(data))
unique_index <- from_the_end(zero_index)
#Если все еще количество "неповторяющихся" нулей не равняется количеству строк в исходной таблице, то..
if(nrow(unique_index)!=nrow(data))
#..Повторяем весь алгоритм заново
hungarian_algorithm(data,optim)
else
#Выводим индексы "неповторяющихся" нулей
unique_index
}
else
#Выводим индексы "неповторяющихся" нулей
unique_index
}
else
#Выводим индексы "неповторяющихся" нулей
unique_index
}
#_________________________________________________________________________________
#__________Функция для нахождения "неповторяющихся" нулей слева-направо___________
from_the_beginning <- function(x,i=0,j=0,index = data.frame(row=numeric(),col=numeric())){
#Выбор индексов нулей, которые не лежат на строках i, и столбцах j
find_zero <- x[(!x[,1] %in% i) & (!x[,2] %in% j),]
if(length(find_zero)>2){
#Записываем индекс строки в вектор
i <- c(i,as.vector(find_zero[1,1]))
#Записываем индекс столбца в вектор
j <- c(j,as.vector(find_zero[1,2]))
#Записываем индексы в data frame (это и есть индексы уникальных нулей)
index <- rbind(index,setNames(as.list(find_zero[1,]), names(index)))
#Повторяем пока не пройдем по всем строкам и столбцам
from_the_beginning(find_zero,i,j,index)}
else
rbind(index,find_zero)
}
#_________________________________________________________________________________
#__________Функция для нахождения "неповторяющихся" нулей справа-налево___________
from_the_end <- function(x,i=0,j=0,index = data.frame(row=numeric(),col=numeric())){
find_zero <- x[(!x[,1] %in% i) & (!x[,2] %in% j),]
if(length(find_zero)>2){
i <- c(i,as.vector(find_zero[nrow(find_zero),1]))
j <- c(j,as.vector(find_zero[nrow(find_zero),2]))
index <- rbind(index,setNames(as.list(find_zero[nrow(find_zero),]), names(index)))
from_the_end(find_zero,i,j,index)}
else
rbind(index,find_zero)
}
#_________________________________________________________________________________
Результат выполнения программы:

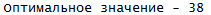
В завершение
Спасибо большое что потратили время на чтение моей статьи. Все используемые ссылки предоставлю ниже. Надеюсь, Вы узнали что-то для себя новое или обновили старые знания. Всем успехов, добра и удачи!
Используемые ресурсы
1. Штурмовал википедию
2. И другие хорошие сайты
3. Подчеркнул для себя немного информации с этой статьи
Комментарии (19)

Pochemuk
02.09.2018 12:01Читал я и терзали меня смутные сомнения, что этот Венгерский алгоритм я уже где-то встречал.
Ба!!! Дык, он же применяется при нахождении приблизительного решения задачи коммивояжера!
Правда, толкового описания, почему этот метод работает для нахождения гамильтоновых циклов в Интернете не найти.
Вот и возникают вопросы:
1. Какая связь между задачей коммивояжера и задачей о назначениях?
2. Если решение задачи коммивояжера венгерским методом находится только приблизительное, то почему решение задачи о назначениях будет найдено точное?
Belyaev_Al Автор
02.09.2018 14:141. Исходный вид матрицы который используется в задачах Коммивояжера практически идентичен тому, который используется в задачах о назначениях. Суть даже одна:
- Если же в задачах о назначениях имена строк/столбцов матрицы содержат работы/работников, то в Коммивояжере и строки и столбцы содержат города (населенные пункты), а сама матрица заполняется либо расстояниями между городами, либо стоимостью.
- В задачах Коммивояжера матрица должна быть так же закрытого типа, и так же, чтобы были «уникальные» значения которые не повторяются в строках-столбце.
- Наверно, единственное отличие — что на главной диагонали матрицы задач Коммивояжера стоят бесконечности.
2. Вот на этот вопрос затрудняюсь ответить. Могу конечно предположить, что задача Коммивояжера тем точна, что во время расчетов мы размер матрицы постепенно уменьшаем, и те значения которые уже найдены мы во внимания не берем. Лишь в конце все складываем в единую картину.
А в Венгерском методе мы решение получаем сразу, и пока задача не решена полностью, мы не можем быть уверены в конечном результате. К примеру, если 4 из 5 нулей найдены, а последний нет, это не будет означать что на новом шаге все «уникальные» нули не изменят свой индекс.

malkovsky
03.09.2018 12:39Хорошей связи между задачей коммивояжера и задачей о назначениях нет… разве что если P=NP.
Наверно речь идет о Christofides algorithm. Есть два известных алгоритма приближенного решения задачи коммивояжера для графа, в котором веса ребер удовлетворяют неравенству треугольника
Простой: находим минимальное остовное дерево, проходим по нему и строим не очень сложным образом цикл. Если выполняется неравенство треугольника, то полученный цикл не более, чем в 2 раза хуже оптимального.
Сложный:
— Находим минимальное остовное дерево
— Находим на вершинах с нечетной степенью в найденном остовном дереве паросочетание наименьшего веса (здесь как раз решается задача о назначениях)
— Находим Эйлеров цикл и несложным образом превращаем его в гамильтонов.
Вуаля, оказывается, что такой алгоритм дает приближение, которое не более, чем в 1.5 хуже оптимального.
Подробнее можно посмотреть тут и тут.

Pochemuk
03.09.2018 13:56Нет… Алгоритм Кристофидеса — это модифицированный алгоритм Эйлера на основе построения минимального остовного дерева.
Он имеет самую лучшую верхнюю оценку для приблизительных методов за полиномиальное время, но существует немало других более простых методов, дающих очень неплохой результат, несмотря на худшую верхнюю оценку. Например, алгоритм Карга-Томпсона (эвристика ближайшей точки — не путать с жадным алгоритмом ближайшего соседа).
Временная сложность АКТ — O(n^3), но степень приближения — достаточно хорошая (хотя в худших случаях и уступает алгоритмам на основе остовного дерева).
Я имел в виду, что Венгерский метод (вычеркивания столбцов и строк) может применяться не только для решения задачи о назначениях, но и для приблизительного решения задачи коммивояжера. Встречал такое утверждение на просторах Интернета.
https://math.semestr.ru/kom/index.php
https://math.semestr.ru/kom/nazn.php

Pochemuk
02.09.2018 15:15+1Наверно, единственное отличие — что на главной диагонали матрицы задач Коммивояжера стоят бесконечности.
Не только…
Задача коммивояжера (поиск гамильтонова цикла) задается на полносвязном графе (пусть даже веса некоторых ребер равны бесконечности), а задача о назначениях — на двудольном.
Т.е., в процессе конференции Иван, конечно, может соединиться с Марией, а Петр с Александрой и Ольгой. Но вот соединять настройку звука с организацией кофе-брейков будет как-то не совсем правильно.
Ну и в задаче коммивояжера мы получаем в результате замкнутый гамильтонов цикл, а в задаче о назначениях — набор несвязных ребер, объединяющий вершины разных долей — работников и работ.

dcc0
02.09.2018 16:30+ в карму. Интересный алгоритм. Отличное объяснение, но не очень понятно, почему результат правильный.

Belyaev_Al Автор
02.09.2018 17:47Спасибо большое! :)
Непонятно почему результат получился именно таким?
Алгоритм считается решенным тогда, когда задействованы все строки и столбцы (ну или как я везде упоминал, найдены уникальные нули).
Быстро набросал картинки для понимания.
В этом случае — задача не решена еще, необходимо либо дальше продолжать алгоритм, либо по второму кругу считать:
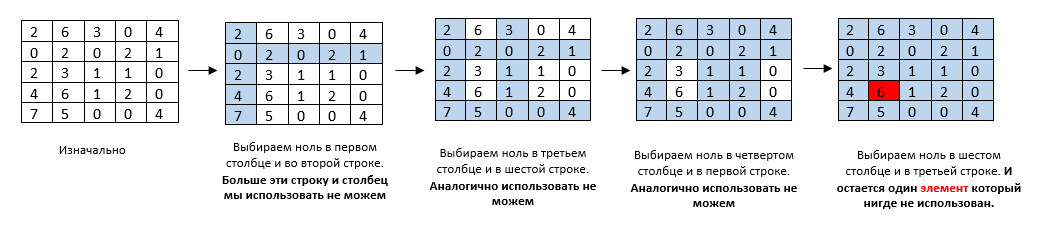
А в этом случае — решение задачи найдено:

Всегда в алгоритме все внимание уделяется нулям. Если бы в первом случае вместо шести был ноль, тогда задача тоже считалась бы решенной. Потом мы индексы нулей (во втором случае где решение задачи найдено — это [2;1],[5;3],[1;4],[4;5];[3;2]) подставляем в самую-самую исходную матрицу, которая у нас была дана изначально с условием задачи. Визуально видим какой исполнитель делает какую работу, и с помощью индексов считаем оптимальное значение.
(Упс, помарочка вышла. Везде где писал «шестая строка»/«шестой столбец» конечно же имел ввиду «пятая строка»/«пятый столбец»)
Если помог разобраться — это супер! Если же нет, с радостью подскажу неясные моменты.

Pochemuk
03.09.2018 00:41Если же нет, с радостью подскажу неясные моменты
Как-то не ясно, зачем 2 раза подряд проводить редукцию по строкам: один раз в самом начале, а второй раз сразу же после нее.
Понятно же, что последует именно это:
Т.к. все минимальные элементы – нулевые, то матрица не изменилась.
Т.е. вторая редукция при поиске максимума явно лишняя.
Belyaev_Al Автор
03.09.2018 17:46При поиске максимума вторая редукция по строкам, по сути, не нужна. Хоть и алгоритм подразумевает ее присутствие, но на деле ею можно пренебречь.
В статью я ее добавил чтобы можно было ссылаться на случай, если кто-либо будет решать задачу на минимум, ну и чтобы алгоритм был, так сказать, полноценным.


MaxVetrov
Как выполнять действия понятно. А почему это работает?
Belyaev_Al Автор
Очень интересный вопрос, попытаюсь ответить:
Потому что каждый шаг алгоритма двигает нас к тому, чтобы получить нули, и чем больше будет нулей, тем быстрее будет найден результат. Если на первом «круге» не вышло найти оптимальное значение, то выйдет на втором, если же и тут решение не будет найдено, можно продолжать алгоритм столько раз, сколько нам потребуется. При этом, каждый раз начиная алгоритм с начала, предыдущие расчеты не сбрасываются, а значит, нулей будет еще больше, что в конечном итоге приведет к решению задачи.
Само же решение, по сути, уже дано изначально, мы лишь делаем необходимые операции для того, чтобы можно было это понять. Нас не интересует какие числа будут в ходе вычислений, все равно в конце мы найденное решение подставляем в исходную матрицу. Легче приводить все числа к нулю, и то, которое быстрее это сделает, и которое будет уникальным в строке-столбце и будет являться если не разгадкой, то направлением к этой же разгадке.
FDA847
Крайне интересный алгоритм! С удовольствием прочитал статью!
Belyaev_Al Автор
Спасибо, приятно! :)
fflush_life
В интернете(даже на той же Википедии) можно найти доскональное доказательство через графы, но оно не самое простое :)
MaxVetrov
Тоже полез туда,) Не просто только если не знаешь теорию графов.
AmartelRU
Объяснение автора кажется мне слишком сумбурным, попробую прояснить вопрос.
1. Добавление константы к элементам одной строки (или столбца) матрицы не меняет оптимальное назначение. Т.е. в результате подобных преобразований суммарная оценка может измениться, но кого куда оптимальнее назначать — нет.
2. После спуска до 0 (так называется операция, выполняемая на первом шаге) мы имеем неотрицательную матрицу. Очевидно, что минимальным будет назначение с нулевыми оценками.
3. «Вычёркивание» нулей минимальным количеством линий — это на самом деле построение максимального паросочетания в двудольном графе, порождённом нулевыми элементами. Найти его можно с помощью алгоритма Куна. Он, помимо элементов максимального паросочетания, возвращает и вершинное покрытие графа (ещё его называют контрольным или контролирующим множеством) — т.е. те самые «вычёркивающие» линии.
4. В том случае, если с имеющимся набором нулевых элементов полное назначение не получается, матрица перестраивается. Разноцветные области из статьи, где элементы увеличиваются\уменьшаются\не меняются — это уже оптимизированная версия того, что происходит на самом деле. Но в такой версии не очевидно, почему подобные изменения матрицы не изменят решение задачи.
А происходит следующее. Мы определяем минимальный «невычеркнутый» элемент и вычитаем его из каждой «невычеркнутой» строки (поэлементно). Это гарантирует нам появление как минимум одного нового нуля, но есть проблема — элементы на пересечении «невычеркнутых» строк и «вычеркнутых» столбцов могут стать отрицательными. Для того, чтобы этого избежать, к «вычеркнутым» столбцам тот же самый минимальный элемент мы добавляем.
Пусть матрица была n*n, i — количество «вычеркнутых» строк, j — количество «вычеркнутых» столбцов. Очевидно, что i + j < n, т.к. иначе существовало бы полное назначение на нулевых элементах и задача была бы решена.
Пусть m — мининимальный элемент, который мы вычитаем. m > 0, т.к. матрица не отрицательна, а все нули «вычеркнуты» (минимальный элемент мы искали среди «невычеркнутых» элементов матрицы).
Мы вычитаем (n — i)*m и добавляем j*m. Добавление j*m — это вычитание -j*m. Таким образом, совокупно мы вычитаем (n — i — j)*m > 0.
Подобная модификация матрицы уменьшает целевую функцию на заведомо положительное число. Целевая функция ограничена снизу — значит, через конечное число шагов минимум будет достигнут.