В марте 2016 года Роберт Дж. Лемке-Оливер и Каннан Соундарараджан из Стэнфордского университета открыли новый шаблон в распределении простых чисел. Оказалось, что простые числа специфически распределяются по числовому пространству. Подробнее см. перевод статьи «Структура и случайность простых чисел» на Хабре.
К изучению темы подключились специалисты из других областей, в том числе химии. И успешно. Профессор теоретической химии Сальваторе Торкуато вместе с теоретиком чисел Мэтью де Курси-Айрлэнд нашли новые шаблоны в распределении простых чисел, о которых раньше не было известно. Оказалось, что распределение простых чисел образует фракталоподобную дифракционную картину, чем-то похожую на картину дифракции у экзотических квазикристаллов.
Профессор Торкуато специализируется на изучении закономерностей в структурах физических систем, таких как кристаллы и коллоиды. Стандартный способ изучения структуры — дифракция рентгеновских лучей. Беспорядочные молекулы в жидкостях или газе отражают лучи во всех направлениях, не создавая заметного рисунка. Но симметрично расположенные атомы в кристалле синхронно отражают световые волны, создавая периодические яркие пятна выраженной дифракции (пики Брэгга). Анализ пиков Брэгга даёт возможность понять внутреннюю структуру кристалла или иного материала, который создаёт такую картину.
Так вот, в новых научных статьях Торкуато и других (1, 2, 3) показано, что обнаруженная упорядоченная структура в распределении простых чисел — ни что иное как фракталоподобная дифракционная картина, примерно как у квазикристаллов.
Картина пиков Брэгга на решётке из простых чисел похожа на квазикристаллы, но всё-таки отличается от них. Торкуато говорит, что простые числа как физическая система «являются совершенно новой категорией структур». Исследователи назвали этот новый фракталоподобный рисунок «эффективной предельной периодичностью» (effective limit-periodicity).
Рисунок состоит из периодической последовательности светлых вершин, которые отражают наиболее общие интервалы простых чисел: все они нечётные (кроме 2), многие рядом друг с другом. Самые яркие пики (пары, разделённые двумя цифрами) чередуются через равные промежутки времени с менее яркими пиками, отражая простые числа, разделённые шестью цифрами. Между ними ещё более тусклые пики, соответствующие более удаленным парам простых чисел и т. д. Всё это — бесконечное количество пиков Брэгга, помещённых друг внутрь друга.
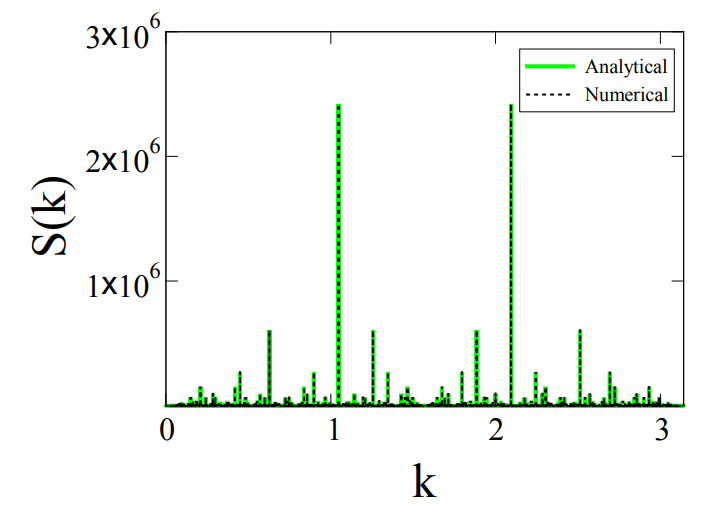
Подобная структура пиков Брэгга наблюдалась и раньше — в дифракционных картинах квазикристаллов.
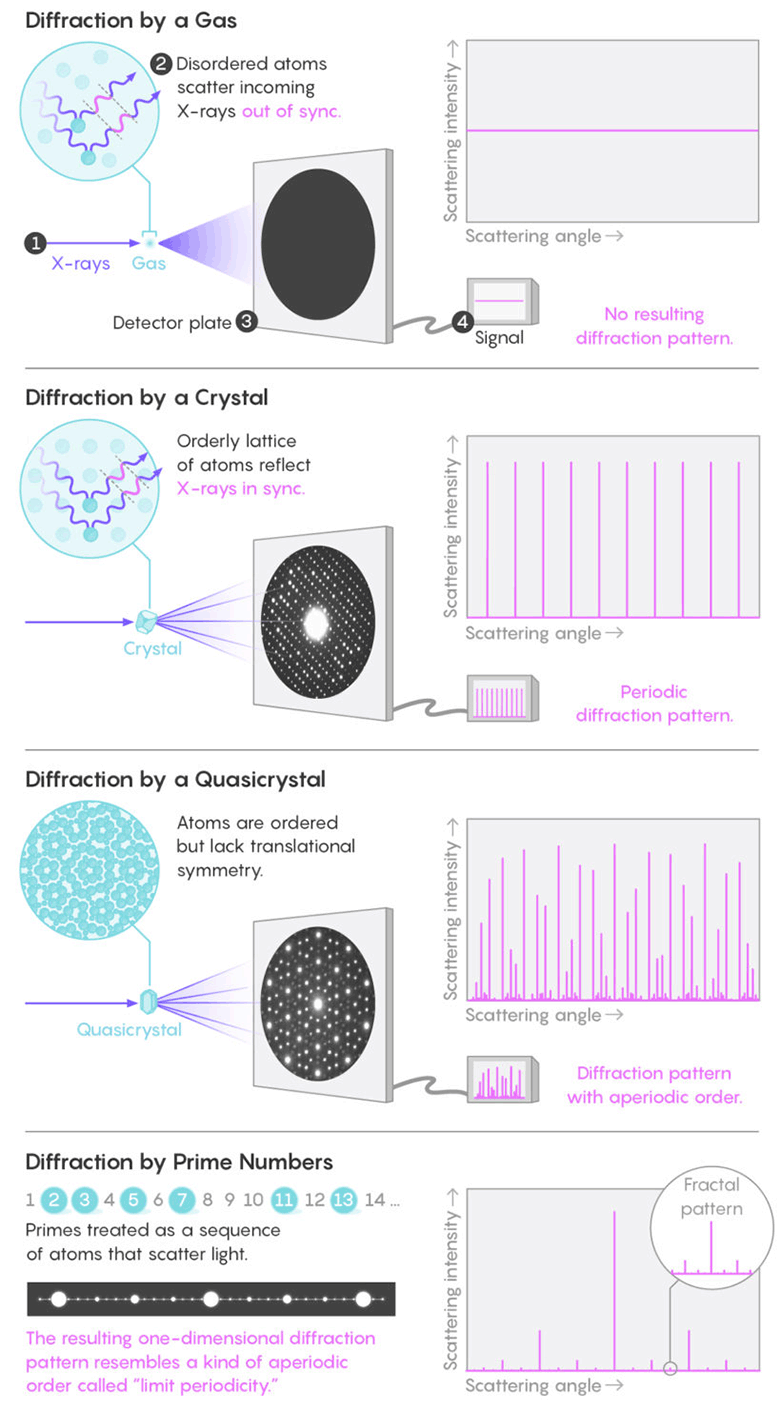
Беспорядочные молекулы в жидкостях или газе отражают лучи во всех направлениях, не создавая заметного рисунка. Но симметрично расположенные атомы в кристалле синхронно отражают световые волны, создавая периодические яркие пятна выраженной дифракции. Как выяснилось, шаблон распределения простых чисел образует фрактальную дифракционную картину, примерно как у квазикристаллов
Квазикристаллы — странные материалы, обнаруженных в 1980-х годах. Они характеризуются симметрией, запрещённой в классической кристаллографии, и наличием дальнего порядка. Математической моделью квазикристаллов являются апериодичные мозаики типа известной мозаики Пенроуза. В таких мозаиках отсутствует трансляционная симметрия, присутствует повторяемость и квазикристалличность (симметрия пятого порядка).
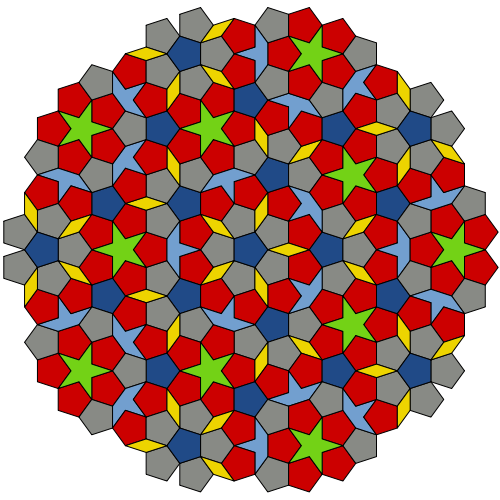
Фрагмент мозаики Пенроуза типа P1 (из плиток шести типов)
В случае простых чисел расстояния между пиками являются пропорциональными частями друг друга, в отличие от иррационально разнесённых пиков Брэгга квазикристаллов. «Простые числа фактически предполагают совершенно другое состояние позиций частиц, похожее на квазикристаллы, но не похожее на квазикристаллы», — сказал Торкуато.
Открытие дифракционной картины нельзя назвать прорывным открытием для теории чисел, потому что основная часть этих шаблонов уже была описана ранее, только другими математическими методами (не через дифракцию квазикристаллов). Так, с помощью дифракционной картины возможно предсказание «двойников» типа 17 и 19 — это математический эквивалент первой гипотезы Харди — Литлвуда относительно существования кортежей простых чисел на данном отрезке числовой прямой. Одно из правил запрещает триплеты из последовательных нечётных чисел после {3, 5, 7}. Это же объясняет, почему следующий по яркости пик Брэгга в дифракционной картине соответствует числам, разделённым шестью цифрами, а не четырьмя.
Новая научная работа — просто свежий взгляд на проблему равномерного распределения простых чисел и более простой способ вывести некий «единый закон» для них. Кроме того, это необычный способ анализа математической проблемы с точки зрения кристаллографии, а именно с точки зрения относительно молодой области исследований, называемой «апериодическим порядком», которая изучает неповторяющиеся модели и лежит на пересечении кристаллографии, динамических систем, гармонического анализа и дискретной геометрии. Эта отрасль науки выросла после открытия квазикристаллов, когда стало понятно, что старые методы тут не работают.
Распределение простых чисел напоминает особый апериодический порядок, известный с 1950-х годов. Он называется предельной периодичностью (limit periodicity). В таких системах периодические интервалы вложены в бесконечную иерархию, так что в любом интервале система содержит части шаблонов, которые повторяются только в большем интервале, как в плитке Тейлора-Соколара.

Плитка Тейлора-Соколара
Теоретические расчёты показывают, что предельно-периодические фазы вещества должны иметь возможность формироваться в природе, и такие системы могут иметь необычные свойства. Но никто не догадался связать предельную периодичность с простыми числами. Теперь мы знаем, что такая связь есть, причём простые числа демонстрируют новый вид предельной перодичности — «эффективную» предельную периодичность, потому что синхронность в расстояниях между простыми числами по всей системе соблюдается только статистически.
Возникает вопрос: как закономерности в распределении простых чисел могут сказаться на стойкости криптографических алгоритмов?
«Я получаю действительно много писем на эту тему. Хотя это интересное исследование, но оно не имеет отношения к криптографии, — написал в своём блоге известный криптограф Брюс Шнайер. — Криптографам не интересен поиск простых чисел или даже их распределение. Стойкость алгоритмов криптографии с открытым ключом типа RSA связана со сложностью факторизации больших составных чисел, которые являются произведением простых чисел. А это совершенно другое дело».
Так что несмотря на прогресс в изучении распределения простых чисел, пока не стоит волноваться за стойкость криптошифров.



uu_69
Представьте, что по числовой прямой слева направо катится колесо с длиной окружности, равной 2. На ободе колеса имеется радиальный выступ, которым оно «выталкивает» из числовой прямой каждое второе число.
Затем по числовой прямой катится похожее колесо с длиной окружности, равной 3. Это колесо убирает каждое третье число и т.д.
Все сохранившиеся на числовой прямой числа будут простыми. Можете представить себе ее вид, после того, как по ней проедет n колес с разной длиной окружности?
Мне кажется, получится нечто похожее на интерференцию волн.
GeMir
С другой стороны, не уверен, что «колесо с длиной окружности, равной 2» так уж легко представить.
KvanTTT
Одно колесо то представить легко, а вот несколько колес, у которых радиусы (не длины) соотносятся определенным образом — сложнее.
StSav012
Радиусы и длины.
ilammy
Классический ответ: представляем колесо с длиной окружности c и полагаем c = 2.
kalininmr
я где то встречал такой вариант описания.
только не колесо, а циркуль мерный.
но идея близкая.
Zhandos_Mambetali
Есть видео как это показали на автокаде:
youtu.be/UYkLz8BIS8k
GeMir
staticlab
Другими словами, n будет простым числом тогда и только тогда, когда
Refridgerator
А там, где есть формула, всегда интересно нарисовать график)
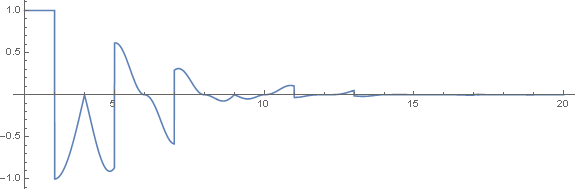
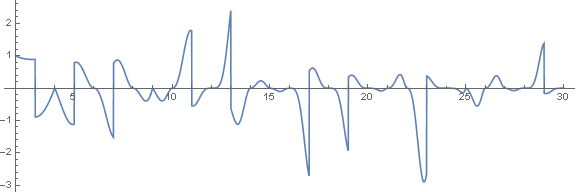
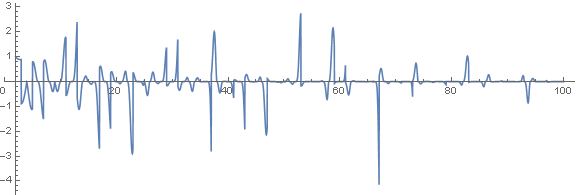
Затухает слишком быстро, поэтому добавил масштабирующий множитель 2n/n2
на большем диапазоне
RomanoBruno
а еще лучше будет гистограмму по модулю сделать, с единичной высотой столбцов
uu_69
Высота столбиков пропорциональна количеству делителей числа.
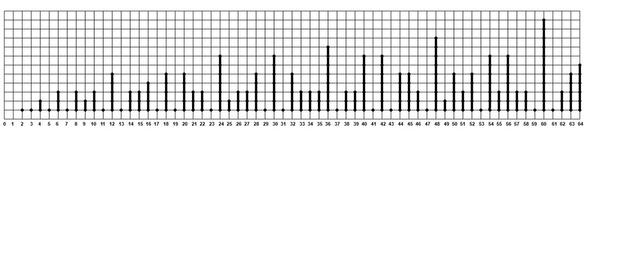
Refridgerator
Ещё так можно:
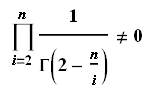

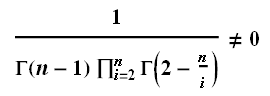
Заменив в гамма-функции n на x, можно полноценный непрерывный график построить, например для n=23:
Более правильно, конечно, так:
чтобы при целых n<2 тоже получать нули.
(Возможно, в произведении n-1 будет достаточно, нужен взгляд настоящего математика)
michael_vostrikov
Zhandos_Mambetali
просто в wolframalpha.com наберите
x mod k,и он выдаст красивую 3d графику.
staticlab
Это вы к чему?
Zhandos_Mambetali
то что любое число x можно проверить на простоту формулой
ibudda
Представить можно все что угодно, хоть голую жопу. Но ненужно забывать, что это позиционная система счисления и любые ритмы в ней естественное явление.
Vantela
Прочитал бы эту статью пораньше, то же б написал такой комментарий.
Ну может не с такой красивой аналогией про колеса, конечно.
Не пойму о чем сыр бор то? Статьи, ученые, еще статьи…
Они реально про принцип решета Эратосфена не в курсе были?
В школе прогу писал еще.
Nikeware
А вы в курсе, что такое аналитический вид функции?
Vantela
Да.
panvartan
те простые числа не такие и простые — они делятся на «пики Брэгга»
pi314
Статья сильно напомнила анекдот, как студент к экзамену по биологии выучил одну единственную тему «бобёр», вытаскивает билет, там «рыба». «Ну, рыба живет в воде. Но у нее, к сожалению, нет длинного плоского хвоста и четырех лап. А если бы были, она была бы как бобёр. А вот бобры...»
amarao
Звучит как «CRISPR в математике». Маленькая революция происходит прямо сейчас.
Barafu_Albino_Cheetah
Если это правда, все должны на ушах стоять. Это же упрощает дальнейший поиск больших простых чисел. На порядки упрощает. А это, в свою очередь, современной криптографии — кувалдой по роже.
staticlab
Быстро находить большие простые числа можно и сейчас. Только задаче факторизации это поможет.
thatsme
Быстро????
KYKYH
Поиск по списку и нумерацию никто не отменял: primes.utm.edu/lists
Есть реально огромные списки.
speshuric
Ну для RSA нужны же простые примерно с половину ключа. Сейчас популярны RSA-2048/RSA-4096. Из-за того, что «плотность» простых убывает достаточно медленно, даже в диапазоне 2^1024...2^2048 можно просто взять случайное число и проверять каждое следующее на простоту. Проверку на простоту на практике делают вероятностным, но быстрым методом Миллера-Рабина.
unC0Rr
Более того, простых чисел в этом диапазоне уже столько, что человечество никогда не переберёт все из них, так что даже готовый полный список никак не мешает криптографии, держащейся на факторизации больших чисел.
pipyakin
Математикам-дармоедама привезли отменную траву?
staticlab
Герман Оскарович, перелогиньтесь.
Mad__Max
Нет, это просто тролль-рекордсмен. Сумел побить рекорд Хабра и собрать заветный значок меньше чем за 10 дней.
NeoCode
Он не Герман Оскарович, а скорее Герман Львович. Вот и в профиле подсказка
tommyangelo27
solovetski
Очевидно, речь идёт о другом Германе, который сказал, что «математики не нужны»: "https://ru.wikipedia.org/wiki/Греф,_Герман_Оскарович
NeoCode
Да я в курсе этого перла :)
wataru
Я как-то пропустил новость, которая все эти мемы породила. Что произошло-то? Почему Греф не любит математиков?
staticlab
Греф сказал, что математические школы не нужны, потому что столько математиков и программистов экономике не нужно.
fatronix
Ну наконец-то отхабрили. Достал, ей богу.
Tortortor
тот, кто писал нашу матрицу, слишком увлёкся переиспользованием кода
halted
Наоборот, теперь смысл простых чисел сильно упрощается и неизвестно еще какие последствия это даст в физике, астрономии и других науках. Той же теории струн например.
Tyusha
Из детства запомнила фантастический рассказ. Люди считали цифры после запятой числа пи. В какой-то момент там началось осмысленное послание толи от высшего разума, толи от внеземных цивилизаций, типа раз вы, человечество, доросли до такого уровня вычислений, пришла пора сообщить вам истину.
Похоже и в распределении простых чисел, кто рисуночек накатал. Смайлик наверное.
Survtur
Карл Саган. Контакт.
x67
Да это ладно, с помощью числа пи в теории фильмы даже смотреть, которые еще не вышли в прокат
MaxxONE
Запретить!!!
RomanoBruno
можно вообще ничего не писать, так как все что вы можете написать все равно есть в числе пи))
michael_vostrikov
Ну если скажем часть атомов отражают в 2 направления, часть в 3, часть в 4, или наоборот, отклоняют лучи с этих позиций, то вполне логично, каждая 2, 3, 4 точка будет иметь некую особенность, которая усиливается при наложении эффектов от других групп. Решето Эратосфена.
yasmax
Скорее здесь не о симметричности, а о дальнем порядке речь, который имеет упорядоченную картину отражения.
Dorogonov_DA
Я не очень могу в математику — она для меня слишком абстрактна, и, возможно, то, что я скажу, может показаться глупым, но повторяется ли эта картина в других системах счисления, с какими-нибудь экзотическими базисами? Универсальны ли оказываются простые числа при переводе из системы в систему?
И лирическое — если распределение чисел напоминает дифракционную картину квазикристалла, то может это и есть тот самый философский камень, который искали столетиями алхимики?
fireSparrow
Любая система счисления, какой бы экзотической она не была, — это всего лишь способ репрезентации чисел. Если вы возьмёте N камушков и сложили их в кучку, то как бы вы не изощрялись с записью числа N, на саму кучку это не повлияет.
Само число не меняет никаких своих свойств от того, что вы его записали по-другому. В том числе и их взаимная делимость остаётся прежней.
alsii
я буду обновлять…
FlameStorm
Я тоже такой себе математик, но определённо сами по себе простые числа существуют вне зависимости от того, по какому базисному основанию их записывают. Да и что бы такого особенного и внезапно подошедшего математике в базисе 2*5, по логике-то. Но в целом присоединяюсь к вопросу.
А лирическое с немного физической стороны… А много ли мы знаем о катализаторах и квантовых эффектах на уровне межатомных взаимодействий? Невозможно исключить существование определённого катализатора, при котором определённый(-ые) из 7 (6) стабильных изотопов ртути, с числом протонов 80 и нейтронов (116,) 118, 119, 120, 121, 122, 124 через относительно холодную ядерную реакцию трансформируются в своего соседа 197-Au с 79 протонами и 118 нейтронами. Ну и что-то побочно соответственно выделяя, конечно — водород там, или нейтрон, или ядро гелия а также прочие нейтрино и фотоны, которые для физика алхимика «и пущай лелят, мне золото надо».
BorisBurkov
Между теорией чисел и кристаллографией/квантами вообще явно есть какая-то связь, они очень похожи. Юрий Манин вот ее долго искал и доискался до квантового компьютера. Интересно, читает ли он эту статью сейчас?
ShamAnton
:-). Это потому что у Вселенной два конца: Один и Тот же…