15.12.2018 10:23
samsergey 90 21100 Источник
Продолжаю знакомить читателей Хабра с главами из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.

Опубликованные главы:
?•? Введение в мерфологию
?•? Закон арбузной корки и нормальность ненормальности
?•? Закон зебры и чужой очереди
?•? Проклятие режиссёра и проклятые принтеры
?•? Термодинамика классового неравенства


В этой главе мы порассуждаем о предопределённости полёта монетки, о топографических картах, о математических катастрофах и о природе случайности. А по пути заглянем в такие разделы математики, как теория мер и теория динамического хаоса.

Разговор о законах подлости, как источнике житейских неурядиц, часто начинается со знаменитого закона бутерброда. Он просто формулируется, легко проверяется и широко известен:
Бутерброд всегда падает маслом вниз.
Понятно, что слово «всегда» здесь — это преувеличение. Легко представить себе условия, в которых бутерброд упадет, оставив намазанную маслом сторону в сохранности. Что же люди понимают, под этим законом? Скорее всего, что бутерброд падает маслом вниз достаточно часто, чтобы это было заметно. Но чаще ли происходит неблагоприятный исход падения, чем благоприятный? Бутерброды разные, падают при различных обстоятельствах, с разной высоты… Параметров столько, что говорить о закономерностях в такой задаче, наверное, нет смысла. Всяко бывает. Бывает, что падает маслом вниз, тогда становится обидно, мы вспоминаем про закон и запоминаем его. А если бутерброд падает неинтересно — маслом кверху, или если он оказался без масла вовсе, так и говорить не о чем — понятно же, что закон-то шуточный! В конце концов, бутерброд подобен монетке, которую математики используют для получения случайных величин с двумя возможными значениями: «орёл» и «решка». Если монетка «честная», то ей абсолютно неважно какой стороной падать, и мы говорим, что вероятность падения орла и решки одинаковы и равны $1/2$. По идее, с бутербродами дела должны обстоять также. Мы вернёмся к ним в следующей главе, а пока присмотримся к самой, наверное, простой вероятностной системе — к монетке.

Монетку в теоретиковероятностных экспериментах подбрасывают каким-то особым магическим образом, так чтобы выбор начального положения, начальной скорости и скорости закручивания при подбрасывании никак не влиял на вероятность конкретного исхода. Но очевидно же, что это невозможно! Монетка представляет собой механическую систему и подчиняется законам механики, а они не содержат в себе случайных величин. Будущее в законах движения такого простого тела как монетка однозначно определяется прошлым состоянием этого тела. Если монетку будет подбрасывать робот, или демон Лапласа — мифическое существо, обладающее полной информацией о координатах и скоростях любой механической системы, то при неизменных начальных данных будут получаться идентичные результаты. Мы, конечно, не роботы и не демоны, но неужели люди подбрасывают монетки настолько неряшливо и непредсказуемо, что законы механики могут приводить к случайностям?

А откуда, вообще, берётся случайность в мире, описываемом законами механики? Откуда вообще, берётся случайность? В чём разница между истинно хаотическими или стохастическими системами, принципиально непредсказуемыми, и системами, в которых просто трудно угадать поведение, но его можно рассчитать?

Задача о монетке рассматривалась в 1986 году Джозефом Келлером. Мы приведём простое объяснение возникновению неопределённости в этом процессе, основанное на рассуждениях из статьи Келлера. То какой стороной упадёт монетка, зависит от времени её полёта $t$ и от угловой скорости $\omega$. Если измерять угловую скорость в оборотах за единицу времени, то число оборотов, совершаемое монеткой, выражается предельно просто $n = t \omega$. Эта зависимость задаёт линии равного числа оборотов в координатах $(t,\omega)$, а они, в свою очередь, ограничивают области, соответствующие чётному и нечётному числу оборотов.

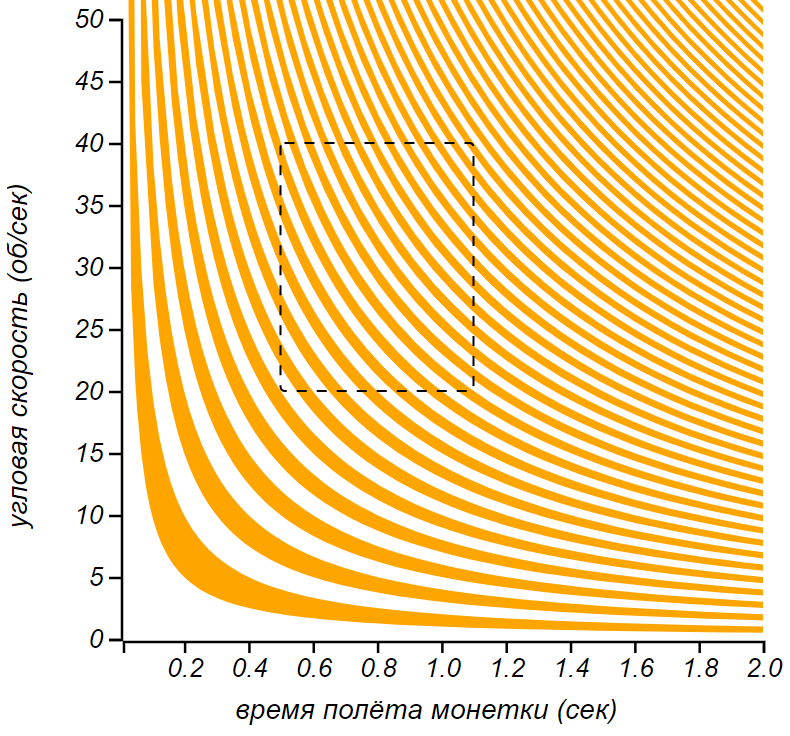
Диаграмма, показывающая чётность количества оборотов, совершаемых монеткой в полёте. Прямоугольником показана область, в которой чаще всего происходит процесс гадания на монетке.

На такой диаграмме можно показать каким будет результат подбрасывания монетки, закрученной на известное число оборотов в секунду, и пойманной через известное время подбрасывания. Если попадаем в белую полоску, то выпадет та же сторона, что была сверху при подбрасывании, если в оранжевую — обратная. Линии равного числа оборотов представляют собой гиперболы и видно, что по мере увеличения числа оборотов, чередование областей становится всё более и более частым, а сами области становятся тоньше. Человеческая рука несовершенна и очень небольшой разброс начальных значений перекрывает сразу много областей, делая исход непредсказуемым. В диапазоне действия руки (прямоугольник на диаграмме) достаточно смещения на $5\%$ чтобы перескочить с белой полоски на оранжевую. Остаётся вопрос: а как из этого построения следует «честность» настоящей механической монеты? Как из полученной диаграммы получить вероятность выпадения орла или решки?

Срочно примите меру!


Окунёмся немного в такую математику, которую не проходят в школе, чтобы лучше понять о чём мы рассуждаем. Мы говорили во введении, что математики изучают не числа или геометрические фигуры, как может показаться после изучения школьного курса. Они работают с математическими структурами (абстрактными алгебрами, полукольцами, полями, моноидами, топологическими пространствами и прочей абстрактной всячиной), описывают их, как кажется, совершенно не привязываясь к практике, определяют их, изучают их свойства, доказывают теоремы. А потом оттачивают мастерство в поиске подобных структур в самых различных областях знаний, совершая удивительно полезные прорывы, в том числе, в чисто прикладных отраслях. Мы сейчас немного коснёмся такой математики и рассмотрим как строится базис теории вероятностей, основанный на весьма абстрактном понятии меры.

Мы описали механику монетки и получили области, описывающие множества решений с определённым свойствами. Области — это плоские фигуры, как правильно перейти от них к вероятностям? Нам нужно измерять наши области и мы естественным образом приходим к их площади. Площадь — является мерой плоской фигуры. Это точный математический термин, обозначающий функцию, ставящую в соответствие множеству некую неотрицательную числовую величину. Примерами мер являются количества в перечислимых множествах (количество яблок в мешке, например), а также длины, площади, объёмы фигур.

В математике существует целый раздел, который называется теорий мер. Эта теория родилась на рубеже XIX — XX веков (у её истоков стояли Эмиль Борель и Анри Лебег) и открыла математикам широкие возможности для анализа очень сложно устроенных объектов: канторовых и фрактальных множеств. Она легла в основу функционального анализа и современной теории вероятностей, фундамент которой был заложен замечательным русским математиком Андреем Колмогоровым. Определение вероятности, как меры, позволяет увидеть все основные свойства вероятности как для дискретных, так и для непрерывных множеств.

Хотя наша книжка не учебник, но на этом стоит немного остановиться, чтобы взглянуть на понятия тории вероятностей как бы с «высоты птичьего полёта» и почувствовать вкус математики. Для начала, перечислим основные свойства любых мер. Для того, чтобы лучше себе их представить, можно использовать вместо слова «мера» слова «количество» или «длина» либо «площадь».
1. Мера пустого множества равна нулю.
2. Мера всего измеримого множества конечна для конечных мер.
3. Мера подмножества не превышает меры множества
4. Мера объединения двух произвольных множеств равна сумме мер этих множеств за вычетом меры их пересечения (аддитивность).
5. Мера дополнения подмножества равна разности мер всего множества и меры подмножества.
Всякая ли неотрицательная числовая функция может быть мерой? Вовсе нет. Например, возраст ставит человеку в соответствие вполне определённое число. Но возраст двух людей нельзя определить, как сумму их возрастов. И скорость бега не является мерой — два человека бегут не в два раза быстрее. А вот импульс (количество движения) или энергия уже обладают свойствами меры. Вес, количество денег, объём знаний, громкость крика хоть и не всегда легко измеримые вещи, но тоже могут служить мерой на множестве людей.

На интуитивном уровне с понятием вероятности знакомы сейчас, практически, все. Её оценивают политологи и журналисты на ток-шоу, её обсуждают говоря о глобальном потеплении или завтрашнем дожде, про неё рассказывают анекдоты: Какова вероятность встретить на Тверской динозавра? — Одна вторая: либо встречу, либо нет. В современной математике понятие вероятность определяется, как мера на особом множестве, которое называется вероятностное пространство. Оно включает в себя как элементарные события, так и их комбинации, получаемые с помощью операций объединения, пересечения и исключения. Пример элементарного события: «выпадение тройки при бросании кости». Пример события, не являющегося элементарным: «выпадение любого чётного числа кроме двойки». Итак, перечислим свойства вероятности:
1. Вероятность невозможного события равна нулю.
2. Вероятность для всего вероятностного пространства равна единице.
3. Если одно событие влечёт за собой также и другое, то вероятность второго не превышает вероятности первого. Здесь отношение «влечёт за собой» для событий эквивалентно «является подмножеством» для множеств и не означает «является причиной».
4. Вероятность наступления хотя бы одного из двух произвольных событий равна сумме вероятностей каждого их этих событий, минус вероятность того, что события случатся одновременно.
5. Вероятность ненаступления события равна один минус вероятность наступления события.
Присмотритесь к свойствам мер и вероятностей и станет видно, что мы говорим об одних и тех же свойствах.

Не все свойства вероятности вытекают из её определения, как меры: понятия независимости событий и способ вычисления вероятности одновременно двух или нескольких независимых событий как произведения из вероятностей вводятся через условную вероятность, но эти понятия согласуются с колмогоровским определением.

Дискретным случайным величинам соответствуют конечные счётные множества, в них естественной мерой является обыкновенный подсчёт количества элементов. Соответственно, вероятностью в дискретном вероятностном пространстве служит комбинаторный подсчёт вариантов, знакомый каждому студенту. Для непрерывных случайных величин, вероятность, как мера, больше похожа на длину или на площадь и тут мы говорим о плотностях вероятности.

Аналогия вероятности с мерой на этом не заканчиваются. Что такое среднее значение? Это аналог положения центра масс фигуры, состоящей из точечных масс или сплошного тела с известной плотностью. И вычисляются эти величины одинаково. А как характеризуется разброс случайных величин вокруг среднего: дисперсия? Также как момент инерции характеризует распределение массы вокруг центра масс. И опять, формулы вычисления дисперсии для выборки или распределения совпадают с формулами для момента инерции набора тел или твёрдого тела хитрой формы.

Кстати, если заменить в определениях и свойствах вероятности сумму на «максимум», а произведение на «минимум», то можно построить альтернативную теорию, она называется теорией возможностей. Так работает математика. Начинаем с абстрактных рассуждений: числа образуют алгебру с операциями сложения и умножения, но на ограниченном числовом интервале можно построить подобную алгебру с операциями минимум и максимум. Строим понятие меры на новой алгебре и выясняем, что она открывает новый взгляд на мир! В отличие от теории вероятностей в такой теории можно построить две согласованные меры — возможность и необходимость, причём они, в отличие от вероятности, хорошо согласуются как с операциями объединения, так и пересечения событий. Это направление созданное американцем Лотфи Заде, азербайджанцем по происхождению, служит основанием для нечёткой логики и используется в системах автоматического распознавания образов и принятия решений.

Невероятно, но факт!


Первое свойство мер кажется тривиальным, но оно интересно своей несимметричностью. Если мера подмножества равна нулю, это не значит, что оно пусто! Например, линия — это подмножество точек плоскости, но её площадь (мера) равна нулю. Бывают и более экзотичные примеры — канторовы и фрактальные множества, имеющие сложную структуру, содержащие бесконечное число точек, зримо «занимающие» некоторую площадь или объём, но тем не менее, имеющие нулевую меру.

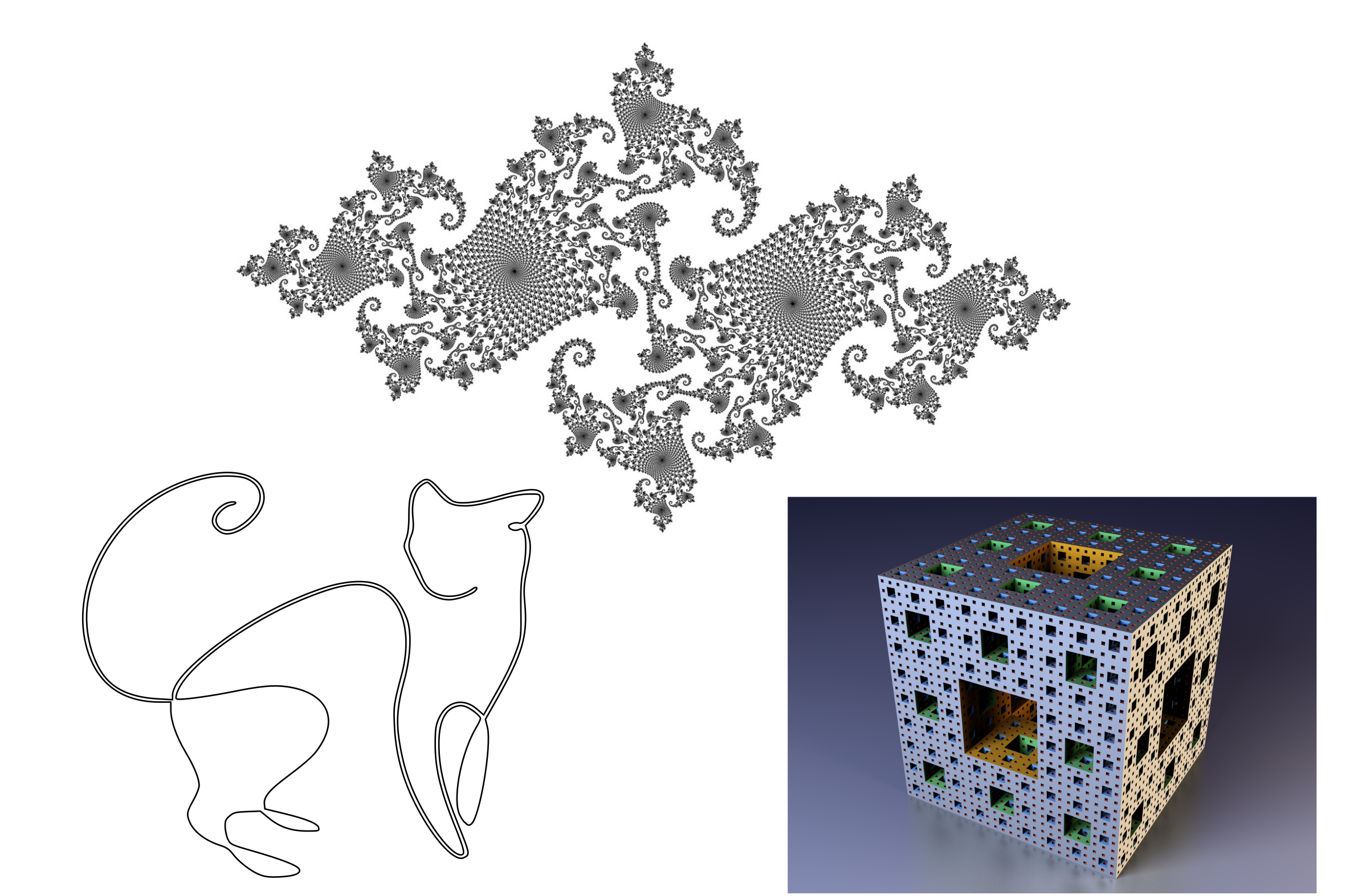Некоторые объекты нулевой меры: линия на плоскости, спорадическое множество Жулиа, фрактальная губка Менгера.

Готовя эту иллюстрацию, я отыскал замечательное изображение несвязного множества Жулиа на прозрачном фоне с высоким разрешением. Вставив его в векторный редактор, я столкнулся с забавной трудностью — было очень нелегко попасть мышкой в это изображение, чтобы выделить его. Оно такое «рыхлое», что вероятность попадания в закрашенный пиксел была заметно меньше попадания в прозрачный фон. В вероятностном пространстве тоже могут существовать подмножества нулевой меры, но это не означает, что события из этих подмножеств невозможны. С четвёртой-пятой попытки я всё же мог выделить изображение, поскольку пиксели имеют конечный размер. Но что было бы, попади в моё распоряжение настоящее несвязное множество Жулиа с бесконечным разрешением?

Представьте себе, что вы пользуетесь программным генератором случайных чисел, который выдаёт произвольное вещественное число от $0$ до $1$. Какова вероятность выпадения числа $0$? а числа $1/2$ или $e/\pi$? Во всех этих случаях ответ будет — ноль! Вернее, самое маленькое доступное компьютеру положительное число, так называемый машинный эпсилон, ведь компьютер оперирует конечным числом знаков после запятой. Подождите, скажете вы, в каком смысле — ноль? Эти же числа не являются невозможными. Давайте проведём эксперимент, в результате мы получим какое-то конкретное число и когда мы его получим, то «по построению» вероятность его появления не может быть нулевой. Всё верно, но сколько нужно ждать до тех пор, пока не выпадет ровно 0? Практически бесконечно! Дело в том, что отдельное число, как точка на отрезке, имеет нулевую меру и честную нулевую вероятность. Отлична от нуля лишь мера сплошного отрезка, пусть даже очень маленького. Так что мы говорим не о вероятности, а о плотности вероятности, которая при умножении на конечную меру подмножества в вероятностном пространстве, даст конечную величину — вероятность попасть в это подмножество. Кстати, окажись у нас идеальный генератор случайных чисел с бесконечной точностью, вероятность получить с его помощью какое-либр рациональное число (не какое-то конкрентое, а вообще любое) тоже будет равна нулю. Доказательство того, что рациональные числа образуют плотное подмножество нулевой меры множества вещественных чисел наделало шума в конце XIX века.

Если кто-то терпеливо проведёт тысячу экспериментов с монеткой и радостно скажет вам, что у него получилось столько же выпадений «орлов», сколько и «решек», можете смело выразить сомнение, либо поздравить его с редкой удачей. Хоть бросание монетки и дискретный случайный процесс, но по мере накопления статистики мощность вероятностного пространства будет расти и мера события: «число „орлов“ совпадает с числом „решек“» будет уменьшаться. Можно показать, воспользовавшись формулой Стирлинга, что вероятность этого «самого вероятного» события стремится с ростом числа испытаний к нулю как $1/\sqrt{\pi n}$. Для сотни бросаний это чуть больше пяти процентов, для десяти тысяч — всего полпроцента. В таких случаях математики говорят: почти наверняка количество «орлов» не будет равно количеству «решек». Как бы странно он не звучал, но «почти наверняка» — это точный математический термин, означающий что событие является дополнением подмножества вероятностного пространства нулевой меры. Мы ещё вернёмся к этим рассуждениям, в одной из следующих глав, когда зададимся вопросом: насколько каждый из нас может считать себя нормальным.

Проверяем честность реальной монеты


Вернёмся к монетке и к её честности. Колмогоровское определение вероятности примирило её частотное определение (как относительной частоты случающихся событий) и геометрическое (как доли «объёма» события в общем «объёме» возможностей). Таким образом, доля площади белых полосок на диаграмме рассчитанной для вращающейся монетки отражает вероятность выпадения той же стороны, которой мы её подкинули.

Но вот беда! Площадь каждой полоски на нашей диаграмме бесконечна (если рассматривать всю четверть координатной плоскости). Однако, аддитивность меры позволит нам аккуратно показать, что это не мешает площадям заштрихованных и белых областей быть одинаковыми. В явном виде уравнения для наших кривых имеют вид $\omega = n/t$. Если площадь под кривой $\omega = 1/t$ равна $S$, то благодаря свойству аддитивности, площадь под кривой $\omega = n/t$ будет равна $S_n = n S$. В свою очередь, для отдельных полосок получаем: $ S_{n} - S_{n-1} = n S - (n-1)S = S$. Выходит, разница площадей не зависит от «номера» гиперболы. Это не что-то особенное, относящееся к гиперболам, тот же вывод можно сделать для любой кривой вида $y = n f(x)$, лишь бы функция $f$ была измерима. А раз так, то для всей области определения, попадания в белую часть диаграммы или в заштрихованную равновероятны, как и ожидается для «честной» монетки.

Рассуждения, которые мы сейчас привели, кажутся достаточно простыми, но они дают весьма общий результат, применимый к любым аддитивным величинам. Абстрактное понятие меры позволило нам сравнивать между собой бесконечные величины, оставаясь в рамках логики и здравого смысла.

Абстракции это хорошо, но можно возразить, что в реальности мы подбрасываем монетки не со всеми возможными параметрами. Как показали эксперименты со скоростной камерой, угловые скорости попадают в диапазон от $20$ до $40$ оборотов в секунду, а длительность полёта — от половины до одной секунды. Эта область выделена прямоугольником на диаграмме. В ней суммарная площадь белых полосок чуть больше чем оранжевых, и можно сделать вывод, что вероятность выпадения той же стороны, что была при подбрасывании, составит $50.6\%$.

В 2007 году группа Перси Диакониса с соавторами из Стэнфорда опубликовала статью, в которой даётся развёрнутый анализ процесса подбрасывания монетки. Детальное описание механики летящего и вращающегося диска, который, не просто вращается, а ещё и прецессирует — ось вращения сама вращается в полёте, показывает, что при ручном подбрасывании из позиции «орел сверху», вероятность выпадения «орла» на одну сотую больше половины.

Много это или мало? Сколько нужно провести экспериментов, чтобы заметить такую разницу? По мере накопления экспериментальных данных, стандартная ошибка среднего, отражающая погрешность, с которой может быть вычислена средняя величина, уменьшается пропорционально квадратному корню из числа испытаний: $\sigma_{\mu} = \sigma/\sqrt{n}$, здесь $\sigma$ — стандартное отклонение для исследуемого распределения. В нашем случае, для распределения Бернулли с вероятностью $0.51$, которое равно $\sqrt{0.51\times0,49}\approx0.5$. Чтобы уверенно выделить отклонение среднего в одну сотую, это отклонение должно превышать $3$ стандартных отклонения. Таким образом, мы можем оценить число испытаний:

$n = \left(\frac{\sigma}{\sigma_{\mu}}\right)^2 = \left(\frac{3\times0.5}{0.01}\right)^2 \approx 22500$

Столько раз нужно подбросить монетку, чтобы заметить механистическую предопределённость результата. Чтобы было понятнее, что имеется ввиду, приведу пример двухсот испытаний идеальной и слегка неидеальной «монеток», проводимых с целью вычислить вероятность выпадения, скажем, орла. Каждое испытание состоит в $40000$ «подбрасываниях». Слова «монетка» и «подбрасывание» взяты в кавычки, оттого, что на самом деле использовалась не физическая монетка, а генератор случайных чисел, подчиняющихся распределению Бернулли.

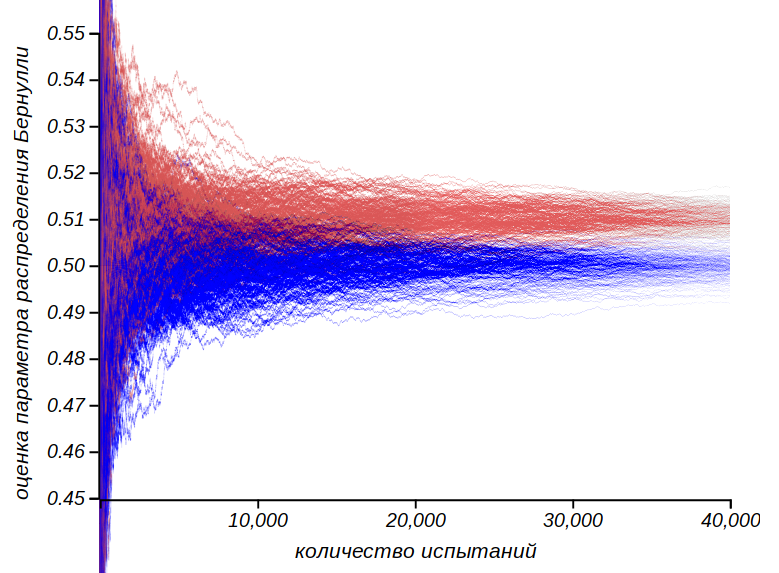
Эксперименты с подбрасыванием идеальной и слегка неидеальной монетки с целью зафиксировать неидеальность.

Видно, что только после $20000$ испытаний «облака» наблюдаемых значений среднего начинают отчётливо разделяться. Что же, для бытового использования можно считать, что монетка — неплохой генератор случайного выбора из двух равновероятных вариантов.

Закон туриста


Эквивалентность геометрического и частотного определения вероятности раскрывает загадку одного закона подлости, известного в кругу туристов, геологов и всех тех, что пользуется топографическими картами:
То место, куда направляется турист, чаще всего оказывается либо на сгибе карты, либо на краю листа.
Предположим, что нас одинаково часто интересуют объекты, расположенные во всех участках карты. Но нас редко интересуют объекты нулевой меры — весь смысл использования карты состоит в обозрении окрестностей объекта, то есть некоторой конечной площади. Пусть нам достаточно будет некоторой малой доли $\alpha$ от площади всей карты $S$, чтобы разобраться в том, как попасть к объекту. Значит, если объект приблизится к сгибу или краю на какое-то критическое расстояние $d$, мы сочтём закон туриста выполнившимся. Доля пограничных площадей в общем площади карты даст нам вероятность испытать этот закон подлости на себе. Вот как выглядят неприятные участки карты при $\alpha=0.5\%$ и одном сгибе.

Серым выделены «нехорошие» участки. Отдельно показан участок с полупроцентной площадью для карты шириной в 40 см, она имеет диаметр слегка превышающий 3 см.

Для квадратной карты $d = \sqrt{\alpha S}$. Неприятные полоски будут иметь площадь $d \sqrt{S} = S\sqrt{\alpha}$. Четыре полосы, две вертикальные и две горизонтальные, расположатся у края, любой дополнительный изгиб, горизонтальный или вертикальный, добавит ещё одну полоску. При этом пересекающиеся полоски добавляют лишние квадратики площадью $d^2 = \alpha S$. Сложив карту так, чтобы получилось $n$ горизонтальных и $m$ вертикальных изгибов, мы получим суммарную площадь неприятной зоны равную: $S(n+2)\sqrt{\alpha}+S(m+2)\sqrt{\alpha}-S(n+2)(m+2)\alpha$. Отнеся её к площади всей карты, получим неприятную долю общей площади:

$p = (n+m + 4)\sqrt{\alpha} - (n+2)(m+2)\alpha.$


На рисунке показаны области, в которых эта доля превышает $50\%$ для различных значений $\alpha$.

Области, в которых повышена вероятность оказаться на сгибе карты или на её краю. Числами отмечена доля площади рассматриваемой окрестности от площади всей карты.

Получается, что карта, сложенная пополам дважды уже может формально считаться нечестной по отношению к туристу. Чаще всего, карты имеют по три вертикальные и три горизонтальные складки, что даёт вероятность выполнения закона подлости с вероятностью около $60\%$ при $\alpha=0.5\%$

Откуда же берётся случайность?


В сувенирных лавках можно найти магнитные маятники для «выбора желаний». Они тоже являются механическими генераторами случайности и их иногда ошибочно называют «хаотическими маятниками». Начав движение с каких-то начальных позиции и скорости, маятник совершает ряд «непредсказуемых» колебаний и, наконец, останавливается в одном из секторов. Однако колебания и здесь не являются непредсказуемыми, просто они очень чувствительны к начальным условиям. Для каждого сектора, в котором может остановиться маятник, существует область притяжения в пространстве координат-скорости. Это множество таких начальных условий, при которых маятник обязательно притянется к определённой точке в указанном секторе. Точка остановки маятника называется аттрактором — притягивающей точкой. В случае маятника с картинки пространство координат и скоростей четырёхмерно, и так просто области притяжения не показать. Но если ограничиться лишь двумя секторами и свести задачу к одномерной (такой маятник называется осциллятором Дюффинга), то пространство начальных значений превратится в плоскость, так что области притяжения можно будет увидеть. Они выглядят как замысловатый символ «Инь-Янь», быстро превращающийся в узкие полоски, разделяющие области притяжения.

Области притяжения аттракторов для одномерного маятника желаний — осциллятора Дюффинга.

Как и в случае с монетой, немного смещая начальные условия мы попадаем от одного аттрактора к другому. Так же действует и игральная кость и рулетка, но они не являются сами по себе генераторами случайности. Это не истинно хаотические системы и их поведение можно точно рассчитать.

А что же такое настоящая случайность? Хороший пример истинно стохастической системы — появление автомобилей на дороге. Люди не договариваются, не согласовывают свои планы, каждый элемент ансамбля за пределами дороги действует независимо. И хотя в поведении людей есть определённые закономерности — часы пик утром и вечером, пустые дороги ночью и т.д., мы не обладаем и никогда не будем обладать достаточной информацией о каждом участнике движения, чтобы предсказать появление любого из них. Также стохастическими являются механика элементарных частиц на квантовом уровне, распад нестабильных атомов, изменения в генетическом коде, по всей видимости, землетрясения и котировки ценных бумаг на бирже. Единственное, что остаётся исследователю, это рассматривать их, как случайные величины и описывать в терминах теории вероятности.

Но есть и другой источник случайностей — динамический хаос. Хаотические системы отличаются от стохастических тем, что описываются точными уравнениями и параметрами, не содержащими случайностей. Однако их поведение не просто сложно, а хаотично и истинно непредсказуемо. Если мы начнём колебать маятник желаний, очень аккуратно, с точно контролируемой частотой и амплитудой, то мы обнаружим, что его плавные движения невозможно просчитать надолго. Никакими алгоритмами на сколь угодно точных вычислительных машинах нам не удастся рассчитать точное поведение маятника на произвольно далёкое будущее. Он не остановится на каком-либо секторе, а будет совершать плавные движения, но никогда не вернётся в одну и ту же точку в пространстве координат-скорости дважды. Ещё один пример предельно простой хаотической системы — идеальный шарик, подпрыгивающий в поле тяжести на идеальном столике с пружинкой. Сравнительно простые уравнения Лоренца показали, что мы никогда не сможем предсказывать погоду больше чем на пару-тройку недель — это тоже хаотическая система.

Теории динамического хаоса, удалось объяснить природу такой непредсказуемости. Простой одномерный маятник желаний, который мы рассматривали, имел две устойчивые стационарные точки — два аттрактора, и одну неустойчивую, от которой система старается уйти, она показана белым кружком. В хаотическом режиме вместо набора аттракторов в системе появляется бесконечное множество неустойчивых стационарных траекторий. Это множество бесконечно, но имеет нулевую меру, и представляет собой очень сложно устроенную несвязную структуру. Попав на одну таких траекторий, в принципе невозможно ей следовать, используя какие-либо конечные алгоритмы. Но самое удивительное, оказалось, что это бесконечное множество неустойчивых траекторий само по себе является притягивающим! 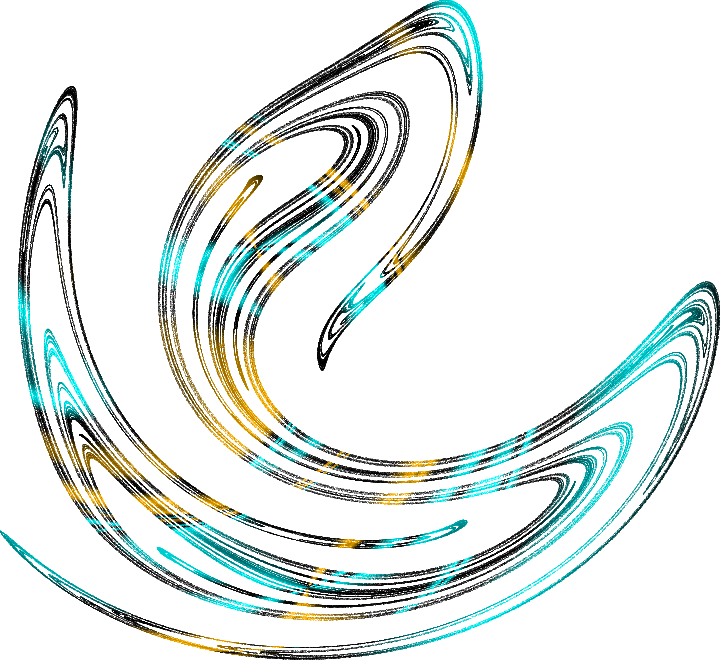Хаотическая система непрерывно перескакивает от окрестности одной неустойчивой траектории к другой, всё время оставаясь в пределах это странного аттрактора. Так эти множества и называются: странные аттракторы. Вот как завораживающе красиво выглядит сечение плоскостью странного аттрактора для маятника желаний, подверженного гармоническим колебаниям. Этот объект для одномерного маятника можно описать в трёхмерном пространстве (координата, скорость, фаза вынужденного колебания). Если рассечь аттрактор в этом пространстве плоскостью то можно увидеть его структуру, это называется сечением Пуанкаре. Каждая точка здесь — это след траектории, а цвет точек отражает относительную скорость с которой траектории разбегаются друг от друга. Вот ещё пара красивых странных аттракторов:


Слева: сечение Пуанкаре для траектории шарика, подпрыгивающего на подпружиненном столике. Множество точек принадлежит поверхности сферы, соответствующей закону сохранения энергии. Справа: объемная область, которая заключает в себе странный аттрактор, рождающийся при вынужденных колебаниях толстой пластины.

Гладкость хаотической траектории позволяет всё же немного заглядывать в будущее. Это объясняет одно досадное наблюдение: с одной стороны, синоптики, порой, не могут уверенно предсказать погоду на неделю, но с другой, если вы скажете, что завтра будет такая же погода, как и сегодня, то не ошибётесь примерно в трёх случаях из четырёх. Вообще же, анекдоты о синоптиках несправедливы и нужно отдать должное человеческой мысли и упорству, которые позволили предсказывать погоду на современном уровне!

Динамический хаос очень сложен и красив как теория, он порождает изумительные по элегантности образы, но он может быть ещё и полезен. Например, алгоритмы, с помощью которых генерируются случайные числа в компьютерах тоже детерминированы. Для примеров в этой книге, я пользовался генератором псевдослучайных чисел, который не запускал реальный стохастический процесс (альфа-распад, или подсчёт машин на дороге), а вычислял следующее «случайное» число на базе предыдущих, полученных им ранее.

От монеток к бабочкам и самой судьбе


Наблюдения за тем, как малые отклонения вырастают в глобальные изменения системы, приводят к мысли об «эффекте бабочки». Напомню, что под этим эффектом подразумевается цепочка далеко идущих драматичных последствий от некоторого незначительного, на первый взгляд, события. Раздавленная исследователями прошлого бабочка в рассказе Рея Бредбери «И грянул гром» привела к кардинальной перестройке будущего. А одну из своих лекций Эдвард Лоренц, создатель теории динамического хаоса, озаглавил так: «Может ли взмах крыла бабочки в Бразилии вызвать торнадо в Техасе?»

На этот эффект мы неявно ссылаемся, сетуя: «Не поверни я за угол, всё было бы по-другому!», «Не сел бы он в этот поезд, с ним не случилось бы катастрофы!» или «Из-за такой мелочи разругались и разошлись!!» Но мы видим, что в мире сосуществуют истинно стохастический квантовый мир и сверхточные атомные часы, устойчивые гамильтоновы системы в мире звёзд и галактик и хаос колец Сатурна или пояса Койпера, тепловое движения молекул и удивительная точность работы биологических систем или механизмов автомобиля. Нет, взмах крыла бабочки не порождает ураганов, а бесследно исчезает, порождая цепочку вихрей, передающих энергию и информацию всё более и более мелким вихрям, покуда и энергия и информация не исчезнут в хаосе флуктуаций. Надо чётко понимать, что малые отклонения приводят к кардинальной перестройке системы лишь, если она неустойчива или если система находится на пороге бифуркации или катастрофы — так на языке математики называются глобальные перестройки в поведении системы при малых изменениях параметров. А бифуркации всегда образуют множества нулевой меры в пространстве параметров — это точки или границы. Малые возмущения не приводят к катастрофам почти всюду, (это тоже точный термин означающий «везде, кроме множества нулевой меры»), а неустойчивые состояния в природе наблюдаются редко, не проходя «проверку временем».

Если пара распалась «из-за ерунды», ей суждено было распасться в любом случае, она была неустойчивой. Устойчивые пары проходят сквозь войны и голод, а потом, бывает и, распадаются, но не из-за мелочей, а в результате глубоких перемен, могущих произойти с личностью в течение жизни. В цепочке событий, приведших к катастрофе поезда нелегко однозначно выделить ключевое событие (конкретную ошибку или роковую случайность) и, скорее всего, ключевым будет не событие, а систематическое нарушение правил, приводящее систему к неустойчивому состоянию. Если в системе множество параметров, и ряд из них случаен, а наша жизнь устроена именно так, то информация в такой системе имеет свойство теряться, и уже никак не удастся восстановить в какой именно момент в нашей жизни «всё пошло не так». Не терзайте себя сожалениями о случившемся, а присмотритесь к происходящему с вами сейчас, чтобы не пропустить настоящей точки бифуркации.

В этой связи можно вспомнить один из законов мерфологии, названный неким Дрейзеном законом восстановления:
Время улучшения ситуации обратно пропорционально времени ее ухудшения.
В качестве примера приводится следующее наблюдение: На склеивание вазы уходит больше времени, чем на то, чтобы ее разбить. Этот закон удивительно точно описывает соотношение между характерными скоростями для процесса релаксации устойчивой системы, которую можно описать убывающим экспоненциальным законом $e^{-\lambda t}$ и скоростью развития катастрофического процесса в неустойчивой системе, в линейном приближении — экспоненциального роста малого возмущения $e^{\lambda t}$. Эти скорости, действительно, обратно пропорциональны друг другу. Пример с вазой, правда, не является релаксацией — переходу к наиболее вероятному состоянию. Он ближе к другому процессу — к самоорганизации, этот процесс, в первом приближении, описывается логистическим законом и ближе по скорости к релаксации, чем к катастрофе.

Типичные нестационарные процессы: катастрофа, релаксация и самоорганизация, имеющие одинаковое характерное время.

$* * *$



Иногда, гуляя в снегопад, я удивляюсь тому, что снежинка падает мне на нос. Удивляюсь оттого, что вероятность этого события была ничтожно мала. Если рассудить, она родилась высоко в небе над Тихим океаном, кружилась в беспорядочных турбулентных потоках в облаке, падала непрерывно меняя направление движения… чтобы попасть на кончик моего носа! А какой ошеломительный путь прошли фотоны от далёкой звезды!? Десятки тысяч лет они неслись сквозь Вселенную, их не поглотила пыль им не встретился астероид! Родились они в квантовом мире далёкой звезды, а закончили свой путь в квантовом мире белка опсина на сетчатке в моём глазу. Даже считать вероятность этого события нет смысла, она равна нулю, но событие случается, и я вижу мерцающий свет звезды. Теперь понятно, что это всё потому, что площадь моего носа и даже молекулы имеют ненулевую меру, но всё равно удивительно: то, что почти наверняка не должно было произойти, всё же происходит!

О предопределённости или случайности судьбы, об истинности или призрачности нашего знания о природе пусть спорят философы. Я же призываю читателя взглянуть на мир с высоты математических абстракций и восхититься его красотой и согласованностью.

Комментарии (90)


  1. vassabi
    15.12.2018 14:04
    #19503870

    А какой ошеломительный путь прошли фотоны от далёкой звезды!? Десятки тысяч лет они неслись сквозь Вселенную, их не поглотила пыль им не встретился астероид! Родились они в квантовом мире далёкой звезды, а закончили свой путь в квантовом мире белка опсина на сетчатке в моём глазу.

    Меня в этом процессе еще поражает (прямо как том в анекдоте): если я вижу так много звезд в небе, это же сколько фотонов так и не попадает мне в глаза (и я не вижу эти астрономические числа звёзд)!


  1. koldyr
    15.12.2018 16:58
    #19504220

    Статья замечательная.
    В "Отлична от нуля лишь мера сплошного отрезка, пусть даже очень маленького." Лишь — лишнее.


  1. Sdima1357
    16.12.2018 01:30
    #19505448

    3. Если одно событие влечёт за собой другое, то вероятность второго не превышает вероятности первого. Отношение «влечёт за собой» для событий эквивалентно «является подмножеством» для множеств.

    Это просто неверно. И очень частая ошибка в логических построениях
    Например, старение влечет за собой смерть, однако смерть может наступить и по другим причинам.


    1. samsergey Автор
      16.12.2018 02:26
      #19505510

      Всё верно, но не торопитесь. Вы говорите об отношении "следствие" (импликация), а третье свойство — всё-таки, о включении. Ваш пример со смертью и старостью, применительно к этому свойству толкуется так: вероятность наступления смерти выше вероятности наступления старости, поскольку, в вероятностном пространстве событие "смерть" является объединением других событий, таких как "старость", "несчастный случай", "самоубийство" и т.д. каждое со своей мерой. Итого — мы все умрём :) Импликация подводит нас к вычислению условной вероятности.
      Колмогоровский подход, дополненный байесовским близок мне именно тем, что он аккуратно отделяет теорию вероятностей от логики, формализуя её на языке теории множеств. В итоге, многое удаётся понять просто рисуя диаграммы Венна.
      Но вы правы, мне стоит подобрать другое слово вместо "влечёт за собой", оно уводит мысль в сторону. Либо привести пример, допустим, ваш, если вы не против.


      1. koldyr
        16.12.2018 12:55
        #19506146

        Пусть А влечёт за собой Б, тогда А лежит в Б, тогда мера А не превосходит меры Б, тогда вероятность А не больше вероятности Б.


      1. sairus777
        16.12.2018 20:32
        #19507208

        Почитайте 5 канонов логики по Д.С. Миллю…


      1. crocodile2u
        18.12.2018 00:36
        #19513224

        Мы все умрем, и каждый умирает с вероятностью единица. Но я живу, и восхищаюсь снежинкой, упавшей на нос или отличной статьей, попавшей в поле зрения...


  1. Refridgerator
    16.12.2018 04:30
    #19505628

    Если одно событие влечёт за собой другое, то вероятность второго не превышает вероятности первого. Отношение «влечёт за собой» для событий эквивалентно «является подмножеством» для множеств.

    В общем случае это неверно потому, что приводит к классической ошибке «после — значит вследствие», и является следствием того, что восприятие нашего мира — одномерно, в котором мы воспринимаем события последовательно, одно за другим. В то время как мир — многомерен и события связаны между собой более сложными связями, чем исключительно «причина > следствие», в том числе и взаимосвязанными.

    Пример.

    С точки зрения курицы в курятнике, сначала включается свет, и только потом появляется человек — из чего она делает вывод, что появление человека является следствием включения света. В то время как на самом деле наоборот — это человек включает свет, т.е. появление света является следствием деятельности человека.

    Примером взаимосвязанных событий являются клеточные автоматы, в частности, игра «Жизнь». Рассматривая переключение состояния клетки с 1 на 0 и наоборот как событие, мы не может установить между соседними клетками причинно-следственные связи, поскольку при расчёте следующего поколения они равнозначны. Рассматривая более сложные композиции такие как «глайдер» — можно интерпретировать их как движение, а причину этого движения найти ранее — например, в «глайдерном ружье». Однако единственной причиной движения «глайдера» является его структура, а непосредственно само движение в него никем не закладывалось — соответственно, и любые причинно-следственные связи поведения «глайдера» являются ошибочными.

    Или же можно вспомнить задачу трёх тел, в котором построение отношений «что вокруг чего крутится» невозможно по определению — хотя и можно сделать упрощения в тех случаях, когда массы тел сильно отличаются.

    Теория вероятностей — это упрощённая модель реальности при отсутствии достаточных данных, а вовсе не основа мироздания. Если, опять же, рассматривать последовательность псевдослучайных чисел — то вероятность угадывания каждого следующего сильно зависит от того, знаем мы алгоритм генерации или нет.


    1. samsergey Автор
      16.12.2018 04:56
      #19505652

      Я ответил на подобное возражение в предыдущем комментарии. Здесь нет речи об условной вероятности либо причинно-следственной связи. Пример со смертью лучше отражает понятие включения. Как только мы усматриваем обусловленность (зависимость), вспоминаем Байеса.


      Любая модель — это модель, упрощение тут не причем. Некоторые объекты реального мира (квантовые явления, например) не моделируются ничем, кроме вероятностей в принципе и никаких достаточных данных тут быть не может. В хаотических системах данных достаточно, но результат все равно останется случайной величиной. Это-то и интересно!!


      1. Refridgerator
        16.12.2018 05:04
        #19505664
        +1

        У вас написано «влечёт», а не «включает», и вы ответили на то сообщение, а не на это. Что во что включает в моих примерах?


        1. samsergey Автор
          16.12.2018 06:10
          #19505720

          Да, я поменяю формулировку, она, действительно, приводит к недопониманию. В ваших примерах нет включения, а есть обусловленность человек -> свет либо свет -> человек. Аксиоматика Колмогорова не описывает понятие независимости событий, это дополнительные определения.


          Про глайдер в Жизни — это интересно. В математике структура кроме множества элементов подразумевает набор отношений с указанными свойствами. В игре Жизнь движение глайдера предопределено правилами автомата. Жизнь — необратимый, но детерминистический автомат, в нем будущее полностью определяется прошлым.


          Отношение "что вокруг чего крутится" очень хорошо строится, просто оно симметрично. Нас же не смущает симметричность в отношении "вершины A и B связаны" в неориентированном графе? Так и тут между тремя телами имеем граф связности и переходим для удобства куда надо. Лучше всего, в центр масс :)


          1. Refridgerator
            16.12.2018 09:04
            #19505816

            Жизнь — необратимый, но детерминистический автомат, в нем будущее полностью определяется прошлым.
            Я слышал, что к реальной жизни это также применимо.


            1. samsergey Автор
              16.12.2018 09:58
              #19505854
              +1

              Ограничено применимо. Кроме проблем с симметрией, в этом подходе есть проблемы с вычислимостью. Однако как модель, она небезинтересна и может быть полезной.


            1. Sdima1357
              16.12.2018 11:23
              #19505998
              +1

              Строго говоря, не очень применима?. В модели Конвея не выполняются законы сохранения. Для ее существования требуется внешний источник энергии, не являющийся частью модели. Физике интересны замкнутые модели. А вот например биологии или социологии открытые.
              А математике и те и другие.


              1. Refridgerator
                16.12.2018 11:53
                #19506032
                +1

                Ну да, это же всего лишь теория, как и теория струн, например. Мне она и самому не особо нравится — так как её следствием является отсутствие свободы воли.


          1. Refridgerator
            16.12.2018 09:25
            #19505834

            Отношение «что вокруг чего крутится» очень хорошо строится, просто оно симметрично. Нас же не смущает симметричность в отношении «вершины A и B связаны» в неориентированном графе? Так и тут между тремя телами имеем граф связности и переходим для удобства куда надо. Лучше всего, в центр масс :)
            Я не совсем понял ваш ответ. Вот тут говорят, что формулировка «земля крутится вокруг солнца» лженаучна, потому что никакого вращения нет в принципе — ни вокруг солнца, ни вокруг любого другого центра масс.


            1. samsergey Автор
              16.12.2018 10:08
              #19505860

              Помню эту статью, хорошая. В ней, как раз, очень хорошо показан формализм, который, собственно и объясняет кто вокруг кого с точки зрения физики. Но тут говорить именно о вращении нельзя — если под вращением понимать круговое движение, ведь траектории некруговые. Впрочем, и это не мешает нам построить отношение "вертится вокруг" со смыслом "находится в сфере тяготения".


      1. Refridgerator
        16.12.2018 05:08
        #19505670

        Некоторые объекты реального мира (квантовые явления, например) не моделируются ничем, кроме вероятностей в принципе и никаких достаточных данных тут быть не может.
        Так и речь тут вроде не о квантовых явлениях, а о макро-объектах, на которые свойства квантовой механики автоматически не распространяются.


        1. samsergey Автор
          16.12.2018 06:31
          #19505724

          Обсуждаемые свойства вероятности относятся к математической абстракции и неважно к чему она применяется.


          1. Refridgerator
            16.12.2018 08:56
            #19505804

            А что, если у математических абстракций есть ограниченная область применимости и за пределами этой области они теряют смысл и приводят к ошибкам? К примеру я слышал, что квантовая механика и теория относительности не пересекаются; а классическая механика Ньютона применима для расчёта баллистических траекторий на небольших скоростях и расстояниях, но не применима для GPS навигации, поскольку время будет утекать.


            1. samsergey Автор
              16.12.2018 10:21
              #19505880

              Ограниченная область применимости есть у моделей реального мира, основанных на математических абстракциях, а не у самих абстракций. Абстракции существуют сами по себе, единственное требование к ним предъявляемое — логическая согласованность (непротиворечивость). "Полезность", применимость к реальности, это выясняется по мере развития естественных наук. Пока полезным оказывается практически всё :)


              1. Refridgerator
                16.12.2018 10:42
                #19505928

                Ограниченная область применимости есть у моделей реального мира, основанных на математических абстракциях, а не у самих абстракций.
                Это лишь другая формулировка, которая ничего не меняет — вы ведь рассуждаете не о чистой математике, а о реальном мире. И пока у вас получается не «теория счастья», а «теория несчастья»; кроме того, у вас нет разделения между «событием» от «интерпретацией события».

                Теория вероятности применима к анализу экспериментальных данных, но совершенно не учитывает человеческий фактор; и уже только поэтому не может автоматически распространятся на все сферы человеческой жизни.


                1. samsergey Автор
                  16.12.2018 12:09
                  #19506058

                  Меняет-меняет, это не просто игра формулировок. Смотрите, группа, алгебра де Моргана, линейное пространство, плотность вероятности, всё это — математические структуры, алгебраические системы или абстракции, не имеющие отношения к реальному миру. С них нет спроса о границах применимости — только строгие определения и свойства, которые можно доказать — не интерпретировать, не приблизить, не придумать, а доказать.


                  С другой стороны, вращение физического тела, течение воды в разветвлённом трубопроводе, скорость материальной точки, местонахождение электрона — это реальные явления и величины и их нужно как-то моделировать. Вращение можно моделировать вещественным числом, кольцом вычетов, группой вращения, матрицей поворота или кватернионом. Скорости удобно описывать, как линейные пространства, но у этой модели есть ограничения при релятивистских скоростях, тогда лучше использовать четырёх-вектор с другими свойствами. Потоки воды и гидравлические сопротивления можно описать алгеброй де Моргана, но не для всех гидравлических сетей, а для некоторого широкого класса. Положение электрона, при описании одних явлений моделируется радиус-вектором, а в других — как случайная величина с известной плотностью вероятности. Модели имеют ограничения, они — упрощение реального мира. Математики, строя свои системы, могут об этом не думать.


                  В этой книжке я рассуждаю, по большей части, о чистой математике. А использую примеры из условно реального мира, как иллюстрации. И я намеренно не рассуждаю ни о психологии, ни об интерпретации событий или о человеческом факторе, поскольку они трудно формализуются и вызывают споры. Моя же задача — показать как устроен математический аппарат теории вероятностей и математической статистики тем, кому это интересно, но кто не получил (ещё) последовательного математического образования.


                  Теория вероятности применима к анализу экспериментальных данных, но совершенно не учитывает человеческий фактор; и уже только поэтому не может автоматически распространятся на все сферы человеческой жизни.

                  Теория вероятностей применима к более широкому классу задач, чем анализ экспериментальных данных (это, скорее, область статистики), но у её создателей никогда не было цели распространить теорию на все сферы человеческой жизни.


                  И пока у вас получается не «теория счастья», а «теория несчастья»;

                  Бартош Милевский иллюстрирует основы теории категории на хрюшках. Но его книги и лекции, всё-таки, не о хрюшках. Моими хрюшками оказались ироничные законы подлости, а называть книжку "Теория несчастья" или "Теория подлости" я не хочу.


                  1. Refridgerator
                    16.12.2018 16:14
                    #19506580

                    Меняет-меняет, это не просто игра формулировок.
                    Но вы же понимаете, что я говорил именно о моделях, а не о математических абстракциях?

                    Модели имеют ограничения, они — упрощение реального мира. Математики, строя свои системы, могут об этом не думать.
                    Да, математики могут не думать. А вот физики думать должны. Задача физики же не в том, чтобы объяснить устройство мира — с этим и теологи прекрасно справляются. Задача физики в том, чтобы миром управлять; и из математических моделей строить реальные устройства. И если работоспособность модели невозможно проверить экспериментом — то ценность этой модели в физике равна нулю.

                    А использую примеры из условно реального мира, как иллюстрации.
                    Вот тут-то я и усматриваю подводные камни, которые могут привести к ошибочным умозаключениям неподготовленного читателя. Одно дело, когда мы бросаем кубик — это эксперимент в чистом виде, в котором влияние непредвиденных факторов сведено к минимуму. И совсем другое другое дело — когда кубик бросает кто-то другой. Этот кто-то может банально утяжелить одну из граней, и тогда все наши статистические вычисления идут к чёрту. В реальной жизни кубик всегда бросает кто-то другой.

                    Моя задача — показать как устроен математический аппарат теории вероятностей и математической статистики тем, кому это интересно, но кто не получил (ещё) последовательного математического образования.
                    Боюсь, что чтобы увидеть математический аппарат — нужно сначала знать, как этот самый аппарат выглядит. А если не знать, то можно увидеть совсем не то, что показывает автор. И самое печальное — можно получить иллюзию знания вместо самого знания — после вашей книги читать Крамера будет очень, очень сложно)

                    Теория вероятностей применима к более широкому классу задач, чем анализ экспериментальных данных (это, скорее, область статистики)
                    «Есть 3 вида лжи: ложь, наглая ложь и статистика»© В частности, помимо корреляции есть ещё и ложная корреляция — и отделение одного от другого может оказаться весьма нетривиальной задачей.

                    называть книжку «Теория несчастья» или «Теория подлости» я не хочу.
                    Ну, есть же ещё много других вариантов названий) А так получается, что никакого счастья быть не может — доказано ведущими стоматологами математиками.

                    Вам знакома книга «Как не ошибаться. Сила математического мышления» Джордана Элленберга? Вот её название совершенно точно отражает содержание.

                    P.S. на всякий случай: вы же просили комментарии, чтобы сделать вашу книгу лучше? Не воспринимайте мои слишком всерьёз — это комментарии гуманитария)


                    1. Refridgerator
                      18.12.2018 11:59
                      #19515128

                      Прошу прощения, опечатался — не Крамера, а Кремера, Н.Ш.


    1. Daddy_Cool
      16.12.2018 16:41
      #19506652
      +1

      «появление человека является следствием включения света.»
      Жизнь она такая — хитрая. Не включится свет — ну там лампочка перегорела — человек пойдет за фонариком. И свет таки будет! А включился свет случайно — замкнуло что-то в выключателе например — человек придет посмотреть что случилось — не воры ли залезли.
      Вот и попробуй объяснить курице, что оно работает как-то по другому. А люди — те же курицы на каком-то уровне сложности задач. )))


  1. withkittens
    16.12.2018 04:30
    #19505630

    Прочитал на одном дыхании. Спасибо!


  1. epishman
    16.12.2018 10:22
    #19505886

    Статья хорошая, но на главный вопрос не отвечает — когда я гадаю на электронных таро или рунах — КТО стоит по ту сторону экрана и выбрасывает карты в зависимости от моего психологического состояния? Да, на будущее прогноз не работает, но картину настоящего дает вполне себе. Я в курсе про самоиндукцию, проекцию, но иногда всеж совпадения ошеломляют. А поскольку эффект лишен повторяемости, сильно зависит от психики и ситуации — научный метод тут неприменим. Пока неприменим.


    1. konchok
      16.12.2018 12:44
      #19506122

      Он не применим потому что это «ТОТ ЖЕ» кто и научные данные сообщает учёным.


    1. koldyr
      16.12.2018 13:52
      #19506280

      По ту сторону экрана сидит эффект Барнума.


  1. dsapsan
    16.12.2018 10:35
    #19505910

    Статья интересная. Но я так и не понял, а причём тут счастье?


    1. samsergey Автор
      16.12.2018 10:36
      #19505916

      "Теория счастья" — это заголовок книжки про несчастья :)


    1. Kuvaldin
      16.12.2018 23:10
      #19507580

      Мне тоже название диссонирует содержанию статьи.
      Я правильно понял, если обобщить всё написанное выше — все случайности носят закономерный характер зависящий от статических переменных?


      1. samsergey Автор
        16.12.2018 23:15
        #19507596

        Нет, не все. В детерминированных системах, чувствительных к начальным данным — полностью закономерный характер. В детерминированных хаотических системах начальные данные тоже влияют, но существеннее вклад сколь угодно малых отклонений в ходе самого процесса. В стохастических системах случайность заложена в саму природу системы и присутствует на уровне уравнений либо параметров.


  1. Refridgerator
    16.12.2018 16:37
    #19506638

    Ещё мне кажется, что вы выбрали не самые подходящие аттракторы для иллюстрации. На аттракторе Лоренца точки бифуркации более очевидны.


    1. datacompboy
      16.12.2018 20:04
      #19507162

      А где в повседревности получить аттрактор лоренца можно наглядно?


      1. Refridgerator
        16.12.2018 20:21
        #19507184

        Вот тут есть немного.


        1. datacompboy
          16.12.2018 21:47
          #19507396

          Ни одномодовых лазеров, ни конвекций в тороидальной трубе я обычно в жизни не наблюдаю.


          1. Refridgerator
            17.12.2018 00:21
            #19507722

            Вот вам более приземлённый пример.

            Вы пошли в магазин за новым айфоном и оказалось, что там две примерно одинаковых очереди. Пока вы выбираете, в какую очередь встать — вы находитесь в неустойчивом положении и ваш выбор со стороны предсказать невозможно. А вот после того, как выбор сделан — пути назад уже нет и траектория до следующей точки бифуркации предопределена; а её устойчивость обеспечивают граждане спереди, сзади и ограничивающие заборы по бокам.


            1. datacompboy
              17.12.2018 00:43
              #19507746

              Ну так и до буриданова осла опустить можно. Только неочевидность по сравнению с примерами статьи зашкаливает


              1. samsergey Автор
                17.12.2018 01:13
                #19507786

                Пример, стати неплохо иллюстрирует последние абзацы главы. В аттракторе Лоренца в режиме развившегося хаоса траектория большую часть времени представляет собой "нормальные" затухающие колебания, пока внезапно её не "выбрасывает" в сопряженную плоскость, где она вновь ведет себя "нормально".


                1. datacompboy
                  17.12.2018 02:38
                  #19507902

                  А можно разжевать на более понятном примере? Я как-то совершенно туплю и не могу проложить параллель.


                  1. samsergey Автор
                    17.12.2018 04:56
                    #19508048

                    Аттрактор Лоренца хорошо демонстрирует один из сценариев развития хаоса — перемежаемость. Система большую часть времени ведет себя детерминировано, но в некоторые моменты перескакивает либо в хаотическое состояние либо в одно из сопряженных детерминированных состояний. И вот эти-то моменты происходят непредсказуемо. Осциллятор Дюффинга тоже имеет такие режимы, при относительно низких частотах возмущения. Однако, я бы не стал обобщать этот сценарий на нашу жизнь: это довольно тонкий эффект, который легко "забить" внешним стохастическим воздействием.


              1. Refridgerator
                17.12.2018 05:57
                #19508088

                Ну так и до буриданова осла опустить можно. Только неочевидность по сравнению с примерами статьи зашкаливает.
                В аттракторах из статьи отсутствуют точки бифуркации, хотя упоминание их имеется; и они постоянно находятся в устойчивом положении, что не является демонстрацией хаоса.


                1. samsergey Автор
                  17.12.2018 06:30
                  #19508120

                  Всё-таки, бифуркации чаще всего относятся к изменениям параметра системы, а не к обобщенным координатам. Поэтому, рассуждая о структуре аттрактора говорят о границах области притяжения, а не о бифуркационных точках. Они находятся в разных пространствах.


              1. Refridgerator
                17.12.2018 09:12
                #19508362
                +1

                буриданов осёл
                Там ситуация другая — у осла есть бесконечное время для размышлений над принятием решения, вследствие чего он и рискует умереть с голода. В нашем же случае время для принятия решения ограничено (в непрерывной модели так и вообще равно нулю), сам выбор неизбежен и вариант «не принимать никаких решений оставаясь на месте» отсутствует. Вместо очередей можно рассмотреть перестроение автомобилей по полосам, а неустойчивость при равнозначном бинарном выборе рассматривается например здесь.


    1. samsergey Автор
      16.12.2018 23:26
      #19507620

      Я выбирал примеры из своей работы и из тех систем, которые легко себе представить. Аттрактор Лоренца стал поп-символом теории динамического хаоса, но он несколько специален и весьма неочевидно связан с метеорологией.


      1. Refridgerator
        17.12.2018 07:20
        #19508190

        Приношу извинения, сглупил — не прочитал описание под картинками.


  1. Refridgerator
    16.12.2018 16:48
    #19506670

    Хороший пример истинно стохастической системы — появление автомобилей на дороге.
    Мне кажется, это не самый хороший пример. Движением автомобилей не управляет случайность. Автомобили не едут в случайную точку в случайное время и по случайному маршруту. Они едут конкретно (например) на работу, по определённому маршруту и в определённое время. Движение автомобилей регулируются светофорами, сервисами типа «Яндекс пробки» или социальными сетями, обеспечивающих (примерно) равномерную пропускную способность на дорогах. Появлению автомобиля предшествует звук мотора, свет фар или переключение светофора с красного на зелёный.


    1. samsergey Автор
      16.12.2018 23:36
      #19507634

      Если в детерминированной системе присутствует стохастический параметр, система становится стохастической. В случае одного транспортного средства такими параметрами являются трудно формализуемые намерения и обстоятельства человека, тесно связанные с намерениями и обстоятельствами неопределённого количества других людей. А для всего потока мы имеем целый ансамбль таких стохастических частиц. Ничто, правда не мешает стохастической системе быть управляемой, закономерно менять интенсивность, создавать волнообразное поведение и т.д. Ну, а то, что моменту регистрации автомобиля предшествует некая "аура" (шум, свет) не делает сам момент более предсказуемым, просто, поле создаваемое аурой сглаживается (шумовой фон над дорогой плавно меняется).


      1. Sdima1357
        17.12.2018 00:09
        #19507690

        что не мешает стохастической системе быть...
        Законы Бойля-Мариотта, Гей-Люссака и Шарля для ансамбля автомобилей :)


      1. Refridgerator
        17.12.2018 05:55
        #19508084

        Тогда получается, что и электрические цепи — стохастические, поскольку движение отдельно взятого электрона отследить невозможно. Но они же как-то работают, и даже рассчитываются через законы Ома, Киргофа и преобразование Лапласа (совсем не статистические методы)?


        1. samsergey Автор
          17.12.2018 06:32
          #19508124

          Так и есть, когда носителей заряда немного, или существуют сильные положительные обратные связи, то наблюдаются стохастические явления: фликкер-шум, например. Обычно же потоки зарядов имеют порядок сотых долей числа Авогадро и флуктуации уже не играют роли, можно методами статфизики или термодинамики переходить к макроскопическому описанию и к непрерывным моделям.


        1. mayorovp
          17.12.2018 09:45
          #19508444

          Стохастический характер системы не мешает существованию общих законов.

          К примеру, все законы термодинамики можно вывести как следствия законов статистической физики.


      1. Refridgerator
        17.12.2018 11:37
        #19508990
        +1

        Если в детерминированной системе присутствует стохастический параметр, система становится стохастической.
        Тогда получается, что абсолютно все системы стохастические, поскольку случайность всегда присутствует на квантовом уровне. Или нет?


        1. samsergey Автор
          17.12.2018 11:57
          #19509134

          Об этом я и хотел сказать, критикуя вульгарный "эффект бабочки": влияние флуктуаций в устойчивой системе не выходит за пределы своего масштаба. Броуновское движение наблюдается на масштабе флуктуаций давления в жидкости, но исчезает уже на сотне микрон — усредняется. По асфальту маленькая бусинка будет катиться стохастически, а шарик от подшипника ровно. И лишь в неустойчивом и неравновесном состоянии: при фазовом переходе, например, флуктуация может стать ядром конденсации и вырасти в каплю или кристаллик.


          1. Refridgerator
            17.12.2018 12:10
            #19509230

            Правильно ли я понимаю, что подмножество стохастической системы вовсе не обязательно должно быть стохастическим?


            1. samsergey Автор
              17.12.2018 14:18
              #19510238

              Не совсем понял, что означает "подмножество". Подсистема?


              1. Refridgerator
                17.12.2018 14:37
                #19510360

                «Подмножество» я употребил в том же смысле, в каком множество целых чисел является подмножеством комплексных. В то время как «подсистема» предполагает разбиение на компоненты.


                1. samsergey Автор
                  17.12.2018 14:56
                  #19510462

                  Всё равно непонятно, у вас размерности не сходятся :) Болтики — подмножество самолёта? Подсистемы могут быть стохастическими, а могут не быть. Идеальный газ — стохастическая система, его подсистема из одной молекулы — нет, из двух — тоже нет. Для сотни молекул уже можно подтвердить гипотезу о том, что их энергии подчиняются распределению Гиббса и говорить о температуре и энтропии с 10% точностью. Для моля газа термодинамика встаёт в полный рост, но всё равно остаются флуктуации. Однако все эти подсистемы — не просто подмножества множества молекул, они обладают системными свойствами: отсутствие взаимодействия друг с другом, сохранение импульса и энергии и т.д.


                  1. Refridgerator
                    17.12.2018 15:10
                    #19510584

                    Одна и та же система может рассматриваться на разном уровне детализации и абстракции.

                    Вот ЭВМ — это же вроде детерминированная система? 2*2 всегда равно 4. Но реализована она на электронных компонентах, которые, по вашему утверждению, детерминированными не являются.


                    1. samsergey Автор
                      17.12.2018 15:26
                      #19510696

                      При токах и температурах процессора и памяти, очевидно, что система вполне детерминирована. Миллиграмм кремния это 28 миллимолей — огромное число частиц! Чтобы получить квантовую стохастику в макромасштабе для квантового компьютера вон как стараются!
                      И, знаете, меня не покидает ощущение, что вы по-доброму дразнитесь, задавая столько вопросов :)


                      1. Refridgerator
                        17.12.2018 15:43
                        #19510824

                        Нет, я не дразнюсь. Как оказалось, моё понимание сути хаоса несколько отличается от вашего. Возможно, в чём-то оно ошибочно. Мне хочется разобраться, действительно ли это ошибка. Если да, то исправить, если нет, то убедиться, что её нет. Ну и всегда приятно пообщаться с умным человеком)

                        Перейду к сути. Если стохастическую систему в виде электронной цепи с неопределённым поведением электронов можно использовать как детерминированную машину для вычислений, то где истина? Какой системой она является на самом деле — стохастической или детерминированной, если физически — это одно и то же устройство?


                        1. nsinreal
                          17.12.2018 16:03
                          #19510992

                          Я влезу в тред извне.

                          Дело в том, что вы не можете просто так трактовать систему с неопределенным поведением компонентов как идеальную детерминированную систему. Но в практическом смысле для всех разумных задач вы можете трактовать некоторые системы как почти идеально детерминированные системы.

                          Математикам различие важно, физикам — по барабану.

                          Замечание: есть ряд случаев, когда можно трактовать систему со стохастическими компонентами как полную идеально детерминированную. Например, стохастический компонент может быть не связан с другими компонентами и не будет влиять на общее поведение системы (является ли это системой — зависит от вашего словаря). Или можно доказать, что стохастический эффект аннулируется (например, у вас есть набор логических вентилей, которые выдают константу вне зависимости от входа). Но, как правило, это никому не интересно.


                          1. Refridgerator
                            17.12.2018 17:47
                            #19511638

                            вы не можете просто так трактовать систему с неопределенным поведением компонентов как идеальную детерминированную систему.
                            А я и не пытаюсь. Я её трактую как модель идеальной детерминированной системы. Моделировать же в обе стороны можно — никто не запрещает моделировать идеальные математические структуры средствами неидеальной бренной реальности.

                            И в рамках этой модели мне совершенно неважна хаотичность на уровне электронов.


                            1. nsinreal
                              17.12.2018 20:32
                              #19512500

                              Тогда можно на ваш вопрос ответить так: одно устройство описывается двумя моделями: и стохастической, и детерминированной.


                        1. samsergey Автор
                          17.12.2018 16:55
                          #19511272

                          Польщен.


                          У Макса Фрая есть такой пассаж: "В море есть остров, на острове — гора, на горе — дуб, на дубу сидит свинья, в свинячьих потрохах — утка, в утке — яйцо, в яйце — микроб, у микроба под язычком — шкатулка, а в шкатулке — САМОЕ ДЕЛО.
                          Так вот, на САМОМ ДЕЛЕ все не так, конечно."


                          Это несерьезно, но отражает суть моего видения мира. Мы с этого начали нашу дискуссию: система одна, она существует объективно и обладает рядом свойств. Но если необходимо её моделировать, то я выбираю наиболее подходящую модель из арсенала исследователя. И ни одна модель, которую я выберу, не будет системой "на самом деле". Впрочем, ряд свойств у них может совпадать.


                          Стохастическая модель бита в ячейке памяти будет тривиальна и неполезна и не будет отражать её свойств. Классическая модель транзистора в ячейке памяти тоже не будет работать, она дает непрерывный энергетический спектр электронов, а он не таков, там есть зоны запрещенные и свободные. И только квантовая модель позволяет точно описать, а значит и построить по модели, реальный транзистор на кристалле. При этом, состояние ячейки, и её взаимодействие с другими, подобными ей, лучше всего описываются полукольцом (булевой алгеброй), что нам и нужно.


                          Динамический хаос моделируется дифурами дискретными отображениями и топологией, однако, ряд его свойств так описать не получается: решения не повторяются, совсем как в стохастических системах, и тогда мы пользуемся вероятностными методами или привлекаем фрактальную геометрию. Ни одна из этих моделей не является исчерпывающей.


                          Если на дорогу выпускать в случайном порядке машины, лучше всего это опишет пуассоновский процесс и подсчет машин в интервал времени будет моделироваться случайной величиной. Но если, мы поставим шлагбаум и будем перекрывать движение, то сможем на какое-то расстояние передавать потоком машин сигналы, скажем, морзянкой. Управление — детерминированное, поток --стохастичный, система — ??


                          Это как с жизнью: атомы точно не живые, аминокислота, белок не живые, клетчатка, РНК, фосфолипиды, сахара не живые. Но РНК плюс белки рибосомы плюс аминокислоты кое что уже могут: собирать другие белки. Чуть повыше: фосфолипидная мембрана, ядро, аппарат Гольджи, хлоропласт, хромосома — не живые. Но митохондрия — пузырек из мембраны с ДНК и ферментами кое что уже может: размножаться, производить АТФ. И так далее. Вирусы — вы кто? Прионы — вы живы или нет? Риккетсии — скорее да, чем нет. Наконец, кошка, вот это точно живая система. Но вдруг, у кошки остановилось сердце. Инфаркт у кошки. Что поменялось? Белки? РНК? рибосомы испортились? Липиды рассосались? Митохондрии передохли? Нет, но кошка уже не живой объект. Это я к чему: начиная с определенного уровня, трудно или даже невозможно однозначно определить характеристику системы.


                          Хаотичность, стохастичность и самоорганизация происходят в достаточно сложных системах, так что границу уже трудно провести. Конвективная ячейка — это самоорганизация, а кристалл — это самоорганизация? а ансамбль молекул дружно двигающихся в одном направлении? наверное, да… а если это падающий кирпич? Не берусь провести границу, хоть занимался этими вещами профессионально.


                          А вот природы квантовой стохастичности я вообще не представляю. Может быть, это следствие истинной гамильтоновости этих систем. Но я принял для себя, что чем бы ни была система "электрон" на самом деле, вероятность его регистрации лучше всего описывается волновой функцией. Он не волна и не частица, он электрон. Это вероятность ведет себя как волна. Подозреваю, что истинные квантовики меня поднимут на смех за такое наивное представление, но оно примиряет с корпускулярно-волновым дуализмом и позволяет решать задачи.


                          1. Refridgerator
                            18.12.2018 06:03
                            #19513670

                            Когда-то давно философы выясняли вопрос, что первично — материя или сознание и познаваем ли мир или нет. Сейчас эти холивары перешли в другую плоскость: что первично — объективная реальность или мат.модель, его описывающая, это реальность хаотична или это модель несовершенна? Может ли математика описать вообще всё или у неё тоже есть ограничения?

                            Можно ли назвать динамическую систему хаотичной, если она однозначно описывается дифференциальными уравнениями? Можно ли фликкер шум считать хаосом, если его спектр не выходит за границы розового шума?

                            На все эти вопросы нет ответа.


                            1. samsergey Автор
                              18.12.2018 08:06
                              #19513898

                              Вы совершенно верно описали дискурс. Я уже писал здесь на Хабре, что математика — последний оплот идеализма в прагматичном мире.


  1. Closius
    16.12.2018 18:21
    #19506914

    А какой ошеломительный путь прошли фотоны от далёкой звезды!?


    Интересно кстати и дургое: Конечно-ли колличество фотонов испускаемое звездой? Фактическо эти фотоны могут быть зафиксированны в точке Х и в точне У. И Х и У могут быть сколь угодно близко. То есть конус фотонного пучка от звезды к нам он же ничтожно мал, но плотность фотонов в нем выходит огромна. Можно ли ее рассчитать? Есть ли такие звезды, которые находятся так далеко, что от них фотоны регистрируются на земле гораздо реже, но регистрируются?


  1. RranAmaru
    16.12.2018 23:16
    #19507598
    +1

    Про бутерброд… Мне тогда лет 14 было. Уронил бутерброд. Естественно, он упал маслом вниз. Так как бутерброд все равно уже был не пригодным в пищу, я решил выяснить, а с какой вероятностью он падает маслом вниз (я уже тогда знал какие-то азы теории вероятности). По результатам около десятка бросаний, и перемазанного в масле пола выяснилось, что вероятность маслом вниз, значительно выше 0.5. Дальше я буквально лег на пол и стал внимательно наблюдать за падающим бутербродом. Оказалось, что падать он может совершенно в произвольном положении, и маслом вниз и маслом вверх и на торец и как угодно. Но! Если бутерброд упал маслом вниз, то он тут же приклеивается к полу. Если строго маслом вверх, то так и остается лежать маслом вверх. А вот если чуть под углом или на ребро, то тут начинается самое интересное — бутерброд чуть-чуть подпрыгивает (упругость хлеба достаточна, чтобы подпрыгнуть на несколько сантиметров), переворачивается и приклеивается к полу маслом вниз. Так что эмпирический «закон бутерброда» действительно существует и никаких законов физики и математики не нарушает.


    1. samsergey Автор
      16.12.2018 23:17
      #19507600
      +1

      Следующая глава посвящена именно механике бутерброда :)
      А вы описали прекрасный пример рождения исследователя!


    1. Sdima1357
      17.12.2018 00:33
      #19507738

      Нужно ещё учесть, что плотность масла (0.9 )значительно больше плотности хлеба (0.4), сопротивление воздуха будет переворачивать бутерброд маслом вниз, как парашют. Видимо метра высоты хватает чтобы эффект был заметен, можно промоделировать на компьютере, сэкономить масло, система то не очень сложная.


    1. TrueZarathustra
      17.12.2018 13:36
      #19509906

      Насколько я помню, проводилось даже вполне научное исследование, которое показывало, что очень сильно влияет высота стола (т.е. сколько оборотов успевает сделать бутерброд). И для типовой высоты столов, а также того факта, что изначально бутерброд лежит маслом вверх — вероятность падения маслом вниз существенно больше 0.5
      А вот если бы столы были выше (точно уже не помню, но кажется ~2 метров), то вероятности были бы другими

      Впрочем, если маслом намазать обильно, то вступят эффекты описанные ниже (масло плотнее и тяжелее), что еще ухудшает шансы падения маслом вниз и, возможно, даже высокий стол не подходит


      1. samsergey Автор
        17.12.2018 14:20
        #19510258

        Разберёмся! :)


  1. aleksandros
    17.12.2018 10:36
    #19508650

    Иногда, гуляя в снегопад, я удивляюсь тому, что снежинка падает мне на нос. Удивляюсь оттого, что вероятность этого события была ничтожно мала. Если рассудить, она родилась высоко в небе над Тихим океаном, кружилась в беспорядочных турбулентных потоках в облаке, падала непрерывно меняя направление движения… чтобы попасть на кончик моего носа!

    Ну, если именно эта снежинка, то да. А если вообще любая, то ничего удивительного, ведь во время снегопада их как песка на пляже)

    Хотелось бы подробнее узнать про идеальный шарик, подпрыгивающий на идеальной пружине. Почему там сложности и невозможно просчитать его движение?


    1. samsergey Автор
      17.12.2018 11:10
      #19508842

      Ну, если именно эта снежинка, то да. А если вообще любая, то ничего удивительного, ведь во время снегопада их как песка на пляже)

      Совершенно верно, мало кто из нас видел метеорит, хотя их полно вморожено о льды Антарктиды.


      По поводу шарика. Если коротко, то это гамильтонова система, в которой возникает разрушение резонансов. Посмотрите, например тут. Хаос по такому сценарию возникает при формировании планетезималей и колец вокруг планет-гигантов, в нелинейных бильярдах, волновых и квантовых системах. Об этом была хорошая статья на Хабре.


  1. dmagin
    17.12.2018 13:55
    #19510058

    Но возраст двух людей нельзя определить, как сумму их возрастов.

    Это выглядит немного натянуто. Почему нельзя? Обычное дело — «им на двоих сто лет».


    1. samsergey Автор
      17.12.2018 14:45
      #19510402

      Если кому-то может быть на двоих сто лет, то сколько же лет мне? Смотрите, я родился сорок лет назад, каждой мое руке — по сорок лет, родились-то мы одновременно, итого — 80! И ногам по сорок, в сумме 160. Но постойте, половинкам рук и ног тоже по сорок, значит, итого получаем 380! А их половинкам… и так далее. Таким образом, получаем что я вечен! А с другой стороны, если возраст моих половинок в два раза меньше моего, то выходит, что каждая из них родились двадцать лет назад. А их половинки — десять лет назад, а их половинки… и так далее. Значит я возник мгновение назад! Причём, сразу сорокалетним, то есть, вечным!
      "Нам тридцать пять на двоих, мы не спускаем друг с друга глаз.." — это поэзия, там можно всё. Но мы на Хабре, у нас математика.


      1. vesper-bot
        17.12.2018 15:21
        #19510668

        «Одно яйцо варится десять минут. Сколько нужно времени, чтобы сварить три яйца?»


        1. samsergey Автор
          17.12.2018 15:56
          #19510942

          О! Тут можно вспомнить про то, что процесс варки можно комбинировать двумя способами: последовательно и параллельно, после чего выдать три ответа!


      1. dmagin
        17.12.2018 17:40
        #19511578

        Поэтичность это здорово ). Но приведенные примеры не слишком убедительны.
        Мысль понятна, просто имхо к возрасту людей не особо подходит.
        Человек может быть по возрасту не делим (на руки и ноги), но аддитивен. Возраст множества людей — обычная линейная функция: age(p1, p2, ...) = age(p1) + age(p2) +… При объединении двух множеств людей возраст множеств складывается за минусом возраста пересечения. Все, как положено.


        1. samsergey Автор
          18.12.2018 12:09
          #19515206

          Тогда всему человечеству 7 * 30 = 200 миллиардов лет? А что с этим числом делать, чему оно соответствует? А ещё наша общая температура 2 триллиона кельвинов, можно не заморачиваться с синтезом! Не все функции аддитивны, даже, если они числовые.


        1. samsergey Автор
          18.12.2018 12:22
          #19515294

          Причем, средний возраст вычислить можно :)


  1. samsergey Автор
    17.12.2018 14:22
    #19510276

    А смысл?


  1. Vlad_fox
    17.12.2018 14:55
    #19510452

    Ни о чем. Какая-то непонятная внезапная прокрастинация про математику и теорию вероятностей.


    1. samsergey Автор
      17.12.2018 15:03
      #19510518

      Ага, прокрастинация глав эдак на десять! С иллюстрациями и формулами… живут же люди! Им ещё за это деньги платят! :)


    1. Refridgerator
      17.12.2018 19:46
      #19512268

      Какая-то непонятная внезапная прокрастинация про математику и теорию вероятностей.
      Это статья вовсе не про математику и теорию вероятностей. Эта статья про монетку, которая ест людей. И про гиперболическую зебру. И про кошечку, которая живёт в кубике с дырками.


  1. Refridgerator
    18.12.2018 12:40
    #19515460

    объемная область, которая заключает в себе странный аттрактор, рождающийся при вынужденных колебаниях толстой пластины.
    Когда речь заходит о колебаниях чего бы то ни было, первое, что приходит в голову — это гармонический анализ. Рассматривали ли вы спектральные характеристики этого аттрактора, а также воздействие на них начальных и возмущающих условий?


    1. samsergey Автор
      18.12.2018 12:48
      #19515536

      Да, это была часть постдока. Это аттрактор шильниковского типа, рождается он в глобальной бифуркации, а не каскадом удвоения, так что спеатр его здорово зашумлён. Где-то есть статья (на корейском языке), где мы с соавтором этого зверя анализируем. Но это было уже 15 лет назад :)