Теория счастья. Термодинамика классового неравенства / forpes.ru

Главная
Теория счастья. Термодинамика классового неравенства

Теория счастья. Термодинамика классового неравенства +40

14.10.2018 10:39

samsergey 106 7600 Источник

Продолжаю знакомить читателей Хабра с главами из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.

Опубликованные главы:

?•? Введение в мерфологию
?•? Закон арбузной корки и нормальность ненормальности
?•? Закон зебры и чужой очереди
?•? Проклятие режиссёра и проклятые принтеры

В этой главе мы порассуждаем о деньгах, рынках и энтропии, а также посмотрим на анимированные гифки, которых, увы, в книжке напечатать не получится.

Наблюдение Хонгрена:
Среди экономистов реальный мир зачастую считается частным случаем.

Экономика — большая, серьёзная, но своеобразная наука. Несомненно, она жизненно необходима, как дисциплина, изучающая реальное и важное явление нашего мира: экономическую действительность. Экономическая наука стремится к доказуемости и формализации, в ней много математики, подчас сложной и интересной. Однако открывая серьёзный экономический учебник, вы, скорее всего, обнаружите какие-то сравнительно несложные выкладки, готовые рецепты и кучу неформальных рассуждений в таком духе: «но на самом деле всё может быть не так и, вообще, как угодно, если на то будет воля ключевых игроков или правительства». В конце концов, может сложиться ощущение, что в этой дисциплине важнее интуиция, знание психологии и умение воспринимать общий контекст, чем точный расчёт и скурпулёзное рассмотрение деталей (речь об экономике, а не о бухгалтерии). Наконец, почти половина липовых диссертаций пишется именно по экономике, стало быть, не так уж и сложно наукообразно рассуждать на экономические темы. Попробуем и мы свои силы на этом поприще, благо, нигде так остро не воспринимается несправедливость этого мира, как в вопросе распределения богатства. К тому же, чем бы ни занимался человек, какой бы профессией ни владел, он вовлечён в экономику и её игры, от законов экономики, как и от законов физики не спрятаться.

Из всей массы задач, решаемых математической экономикой, мы рассмотрим лишь одну — каким образом получается так, что даже при равных условиях для всех участников рынка и справедливом обмене средствами бедных становится больше чем богатых и почему даже идеальное математическое общество оказывается склонно к финансовому неравенству. Ну, и попутно узнаем кое-что любопытное о математической статистике и распределениях случайных величин.

Я физик по образованию и по профессии, и моя профессиональная деформация выражается в своеобразном взгляде на мир, как на множество разнообразных физических систем и процессов. С точки зрения физика, реальный рынок — это существенно нестационарная открытая система, со множеством степеней свободы, в которой важную роль играют стохастические (случайные) процессы. В этом смысле рынок похож на предмет изучения таких разделов физики, как термодинамика и статистическая физика, в которых, ввиду невозможности рассмотреть всё неисчислимое количество деталей и поведение всех составляющих частей системы, переходят к обобщающим и измеримым её свойствам, таким как энергия, температура или давление. Неудивительно, что попытки термодинамического описания экономических систем и создания эконофизики предпринимаются уже более ста лет. Но вот беда: пока учёные рассматривают детали, обобщают полученные знания и ведут споры о фундаментальных законах, основной объект изучения — экономическая действительность, успевает поменяться до неузнаваемости. Её поведение как будто стремится сохранить, а то и увеличить свои неопределённость и непредсказуемость.

Хорошим примером служит двухвековая история использования технического анализа при игре на фондовой бирже. Когда появляется новый мощный инструмент, позволяющий нащупать скрытые закономерности и предсказать курс ценной бумаги или акции, он начинает приносить прибыль тем, кто его использует. Но вскоре рынок начинает «чувствовать» новых игроков и подстраиваться под их стратегию, точность предсказаний замечательного метода начинает падать и, спустя какое-то время, он попадает в большой список устаревших и не слишком надёжных инструментов. Ни современные гибкие самообучающиеся нейросетевые алгоритмы, ни сверхскоростные роботы-трейдеры, совершающие миллионы операций в минуту, не поменяли за минувшие два десятилетия основное свойство биржевой игры — её непредсказуемость. И до сих пор основными достоинствами профессионала в этой отрасли являются воля, выдержка характера, несклонность к азарту… ну, или владение биржей. Всё как в казино, где игры основаны на чистой случайности! С одной стороны, это, конечно, обидно, а с другой — даёт повод постоянно совершенствовать методы и подходы. Когда-то и теория вероятностей и математическая статистика родились из попыток анализа азартных и экономических игр и только потом нашли применение почти во всех естественных науках.

Мы в дальнейших рассуждениях будем говорить о деньгах, но эта привычная повседневно используемая категория на удивление сложна и неоднозначна. Смысл и ценность денег зависит от множества факторов, и называя вне контекста некую денежную сумму, мы ничего не говорим о её реальной ценности. Это отличает денежные величины от большинства физических величин, описывающих наш мир и здорово мешает проводить строгие рассуждения в экономике. Но цель нашего разговора: математические основы законов подлости, повседневных, понятных и простых. Поэтому в дальнейшем мы будем говорить о неких «рублях», имея в виду формальный билетик или монетку, и подразумевая, что чем больше этих «рублей» у кого-то, тем он «богаче». Прочие же рассуждения о покупательской способности, нематериальных или неликвидных ценностях, о «не в деньгах счастье», наконец, мы оставим за рамками разговора.

Подходите, всем хватит!

Начнём с анализа справедливости некоторых простых стратегий раздачи известного количества денег конечной группе людей.

Первая, самая очевидная стратегия: «взять всё, да и поделить», то есть выделить каждому члену группы по равной доле общей суммы. Такое распределение называется вырожденным, оно имеет индекс Джини равный нулю и соответствует кривой равенства на диаграмме Лоренца.

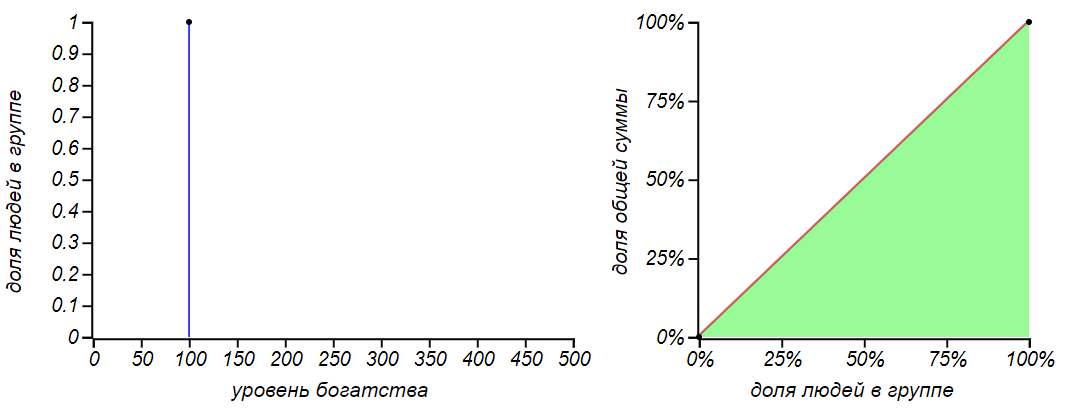
Абсолютно справедливое вырожденное распределение денег: у всех всё поровну.

Прекрасный вариант! Назовём его «стратегией Шарикова» в честь героя повести Михаила Булгакова «Собачье сердце», который именно таким способом предлагал решить все экономические вопросы.

Вторая, более реалистичная стратегия заключается в многократной раздаче всем по одному рублю в случайном порядке. Кому как повезёт. Можем назвать эту стратегию «пуассоновской», поскольку именно таким образом распределяются по временной шкале независимые случайные события в процессе Пуассона. Для группы из

$inline$ человек вероятность каждого из участников получить рубль составляет

$inline$ . После раздачи таким образом

$inline$ рублей, каждый должен получить сумму равную количеству таких «положительных» исходов. Функция вероятности для подобной суммы хорошо известна — это биномиальное распределение, похожее на колокол, симметрично разбегающийся вокруг среднего значения

$inline$ . Обычно с ним знакомят на примере вычисления вероятности получить указанную сумму, бросая игральные кости. Для больших значений

$inline$ биномиальное распределение становится практически неотличимым от нормального. Давайте посмотрим как будет меняться, по мере раздачи денег, распределение денег в группе и его справедливость.

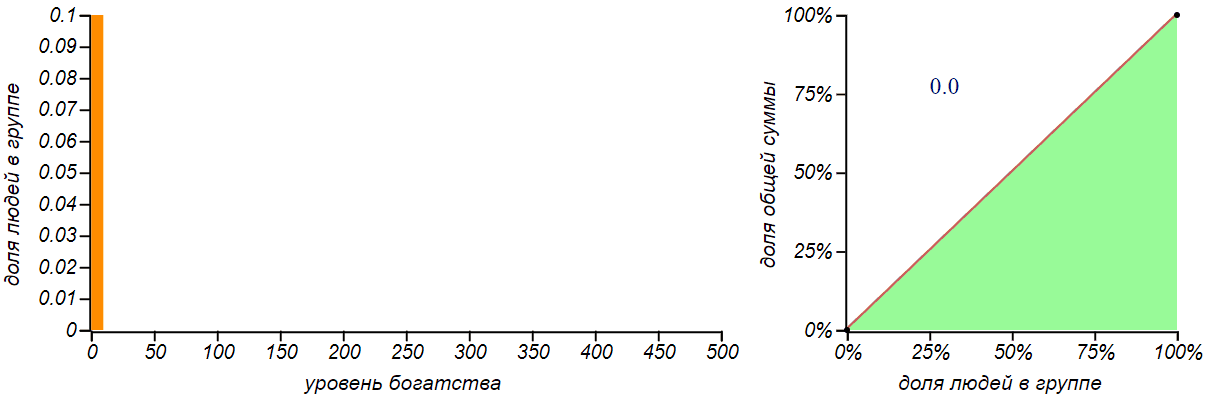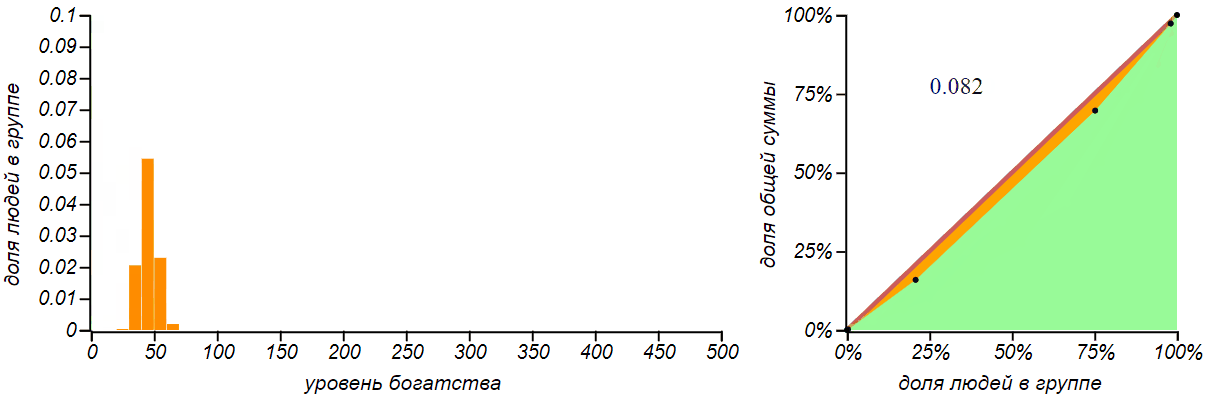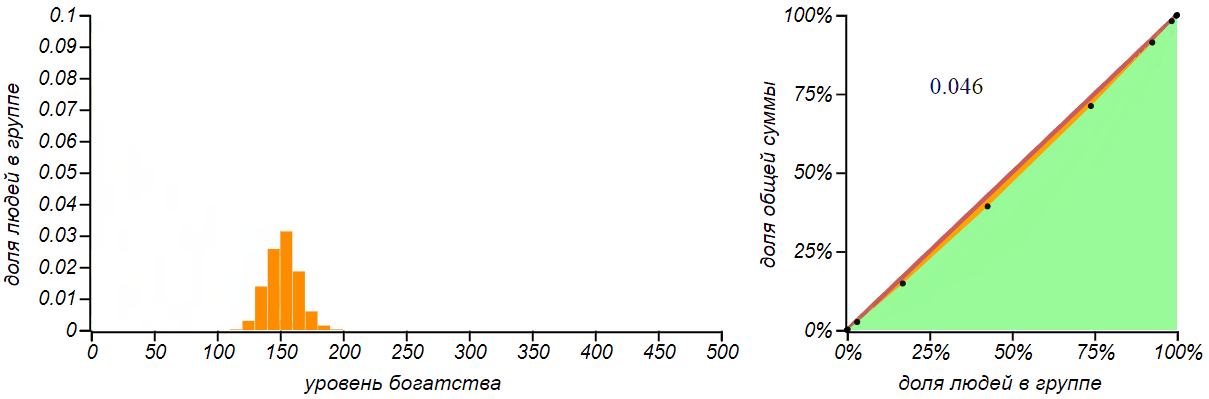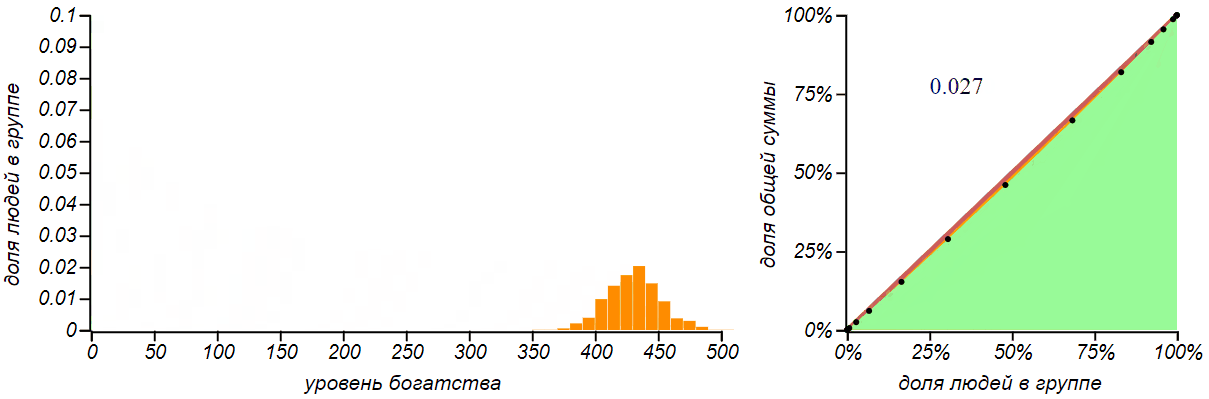
Результатом раздачи денег по принципу «на кого бог пошлёт» является биномиальное распределение. Чем больше денег мы раздаём, тем больше становится значение среднего и разброс, но вероятность не получить ничего практически исчезает.

Алгоритм пуассоновской стратегии

Исходные данные: xs — массив из n элементов, заполненный нулями, M — общее количество денег в системе.
Повторить M раз
    i <- случайное целое от 1 до n
    xs[i] <- xs[i] + 1

Это распределение, с точки зрения справедливости, очень неплохо выглядит, более того, оно становится тем справедливее, чем больше денег мы раздаём публике! Просто замечательно! Жаль, что общество устроено не так и дождь из денег не сыплется на всех нас поровну.

Для полноты картины, давайте рассмотрим ещё одно простое искусственное распределение денег — равномерное. При таком распределении бедных будет столько же сколько и богатых.

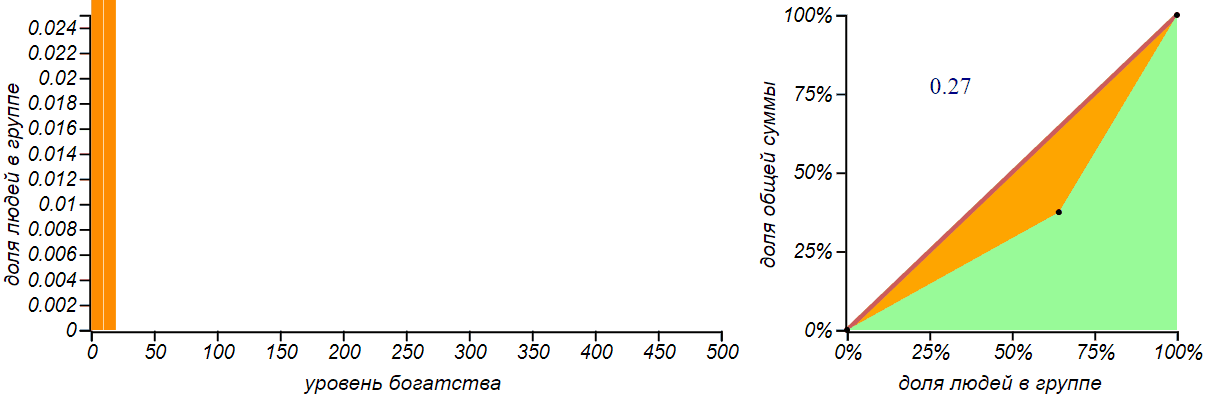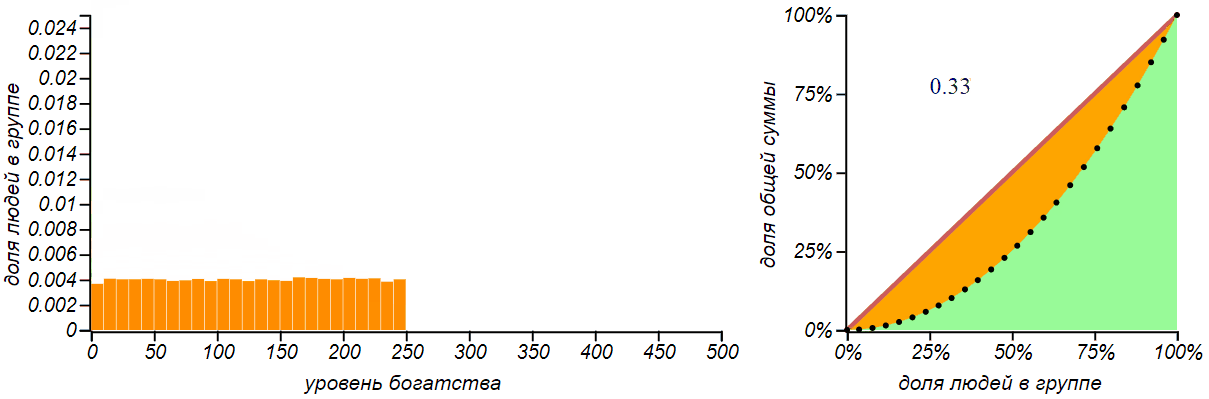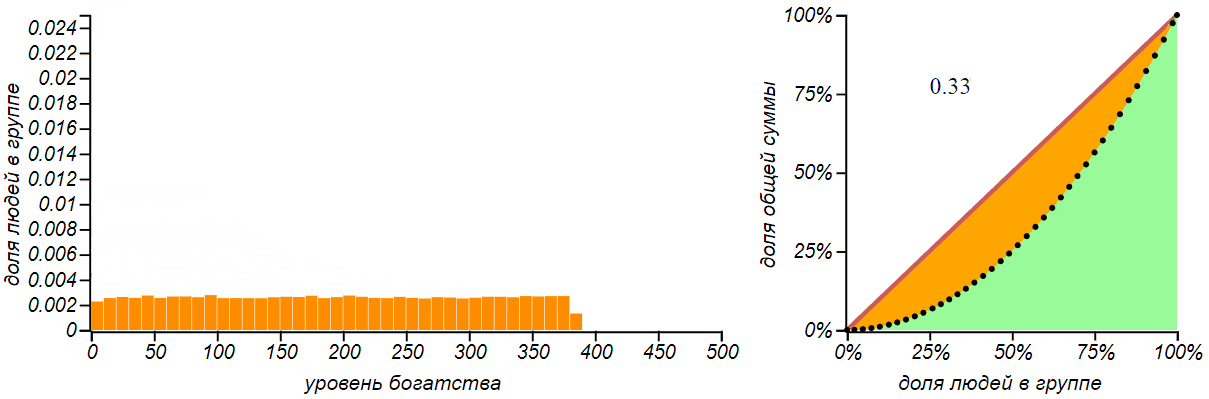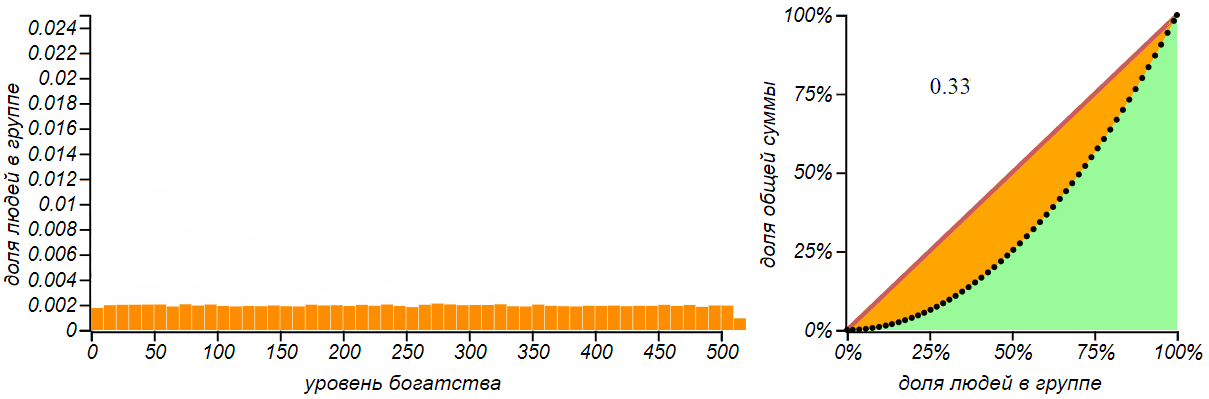
Равномерное распределение не означает, что деньги распределяются по всем равномерно. При таком распределении число богатых, бедных и середнячков одинаково, но деньги в основном принадлежат богатым.

Алгоритм стратегии равномерной раздачи

Исходные данные: xs — массив из n элементов, заполненный нулями, M — общее количество денег в системе.
Для каждого элемента x из массива xs
    x <- случайное целое от 0 до M/n

Для равномерного распределения кривая Лоренца представляет собой квадратичную параболу, а если левая граница распределения равна нулю, то эта парабола независима от положения правой границы, и индекс Джини для всех таких распределений равен в точности

$inline$ . Такое значение индекса (но не такое распределение!) был, например у экономики Австралии в 2000-е годы — это вполне неплохой показатель.

Однако рынок есть рынок! Рассмотренные выше распределения хороши, но требуют специальных условий для своего возникновения. Если дать людям волю обмениваться деньгами, менять деньги на услуги, копить их и проматывать в одну ночь, идеальные распределения потеряют устойчивость и превратятся в какие-нибудь другие.

Новая экономическая политика!

Рассмотрим группу из

$inline$ человек. В результате революции раздадим всем участникам эксперимента по равной денежной сумме — по

$inline$ рублей каждому, получив самое справедливое шариковское распределение средств в обществе. Теперь предоставим им свободу богатеть и беднеть по воле собственной судьбы и построим примитивную модель рынка. Попросим кого-нибудь, случайно выбранного, отдать один рубль любому человеку из группы, так же выбранному случайно. Скажем, что это приобретение некой услуги по фиксированной цене. Распределение богатства ожидаемо изменится: у кого-то денег станет меньше, у кого-то больше. Станем повторять процедуру обмена снова и снова и посмотрим на то, как будет изменяться распределение богатства в группе.

Разумно перед проведением эксперимента поразмыслить, что же мы ожидаем увидеть. Обмен деньгами между участниками происходит равновероятно, как в случае пуассоновской стратегии раздачи денег, но в тоже время игроки и теряют деньги, причём по такому же пуассоновскому принципу и с такой же интенсивностью. Таким образом, можно предположить, что как положительные, так и отрицательные приращения будут нормально распределены и расположены симметрично относительно нуля. Каждый игрок, в конечном итоге, будет получать разность этих приращений, которая для двух нормально распределённых случайных величин будет тоже нормально распределена, в данном случае, вокруг нуля, так как потери и выигрыши симметричны.

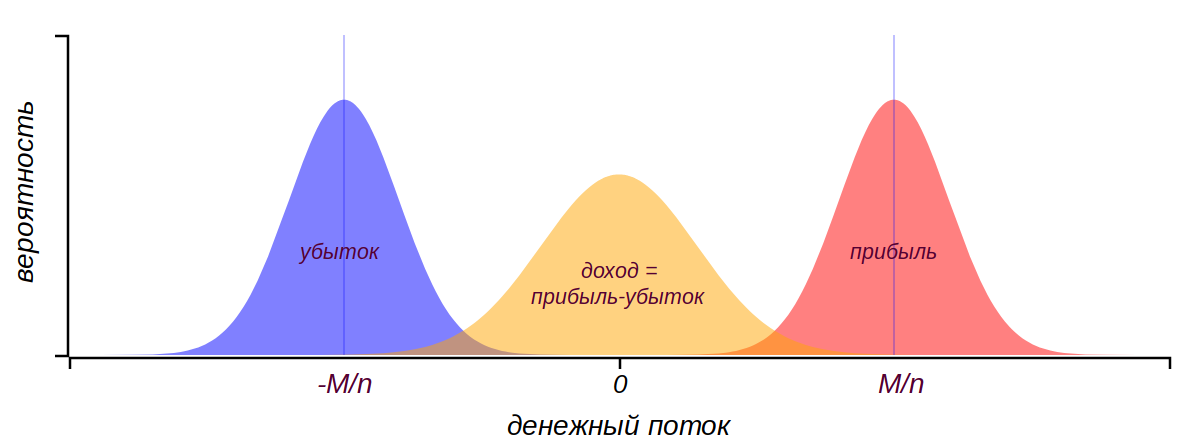
После множества обменов каждый игрок получит и потеряет сумму, подчиняющуюся распределению, близкому к нормальному. Суммарный доход также будет нормально распределён вокруг нуля.

Таким образом, мы получаем классическое случайное блуждание с нормально распределёнными приращениями и можем ожидать некой диффузии средств вокруг среднего значения

$inline$ . Функция вероятности должна размываться, увеличивая дисперсию при неизменном среднем значении. Вроде бы, всё просто.

Но есть нюанс. Если, по каким-то причинам, у кого-либо из группы не осталось средств, он не сможет приобретать услуги, отдавая деньги, но, в тоже время, может их получать. Возможное значение благосостояния ограничено слева нулём, а значит диффузия богатства не сможет распространяться бесконечно и наблюдаемая функция вероятности, рано или поздно, перестанет быть симметричной.

Есть ещё один нюанс. Количество денег в нашей замкнутой системе ограничено и неизменно, это значит, что случайные блуждания не независимы. Какой-нибудь везучий игрок сможет получить очень большие суммы и уйти от ансамбля очень далеко, но только если общая масса обеднеет. Участников эксперимента стягивает невидимой сетью закон сохранения денег в системе. К чему же будет стремиться распределение денег таких условиях? Похоже, ответ не столь очевиден, как может показаться на первый взгляд, давайте обратимся к имитационному моделированию и посмотрим что у нас получится.

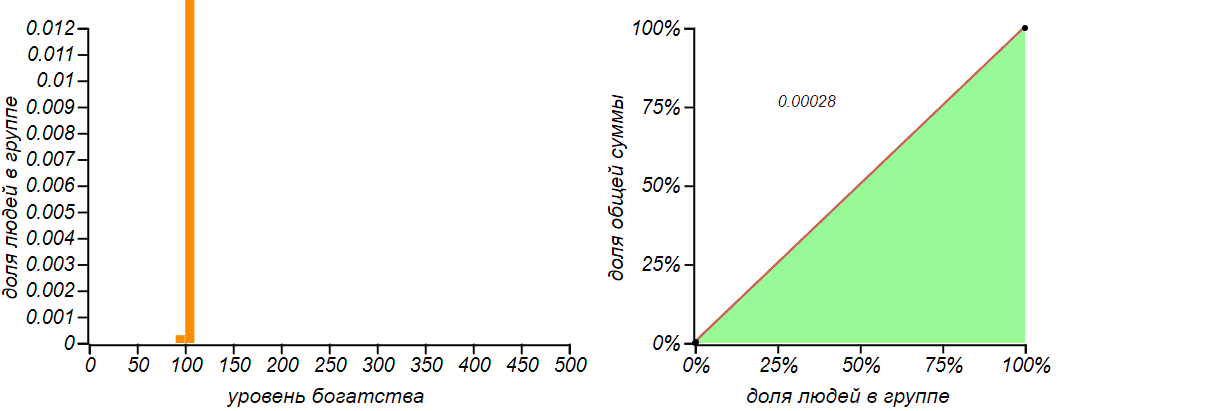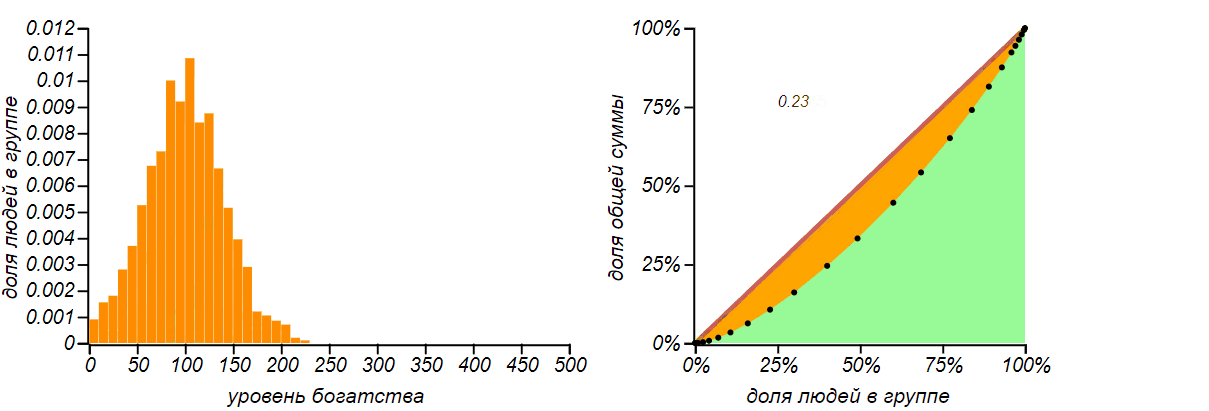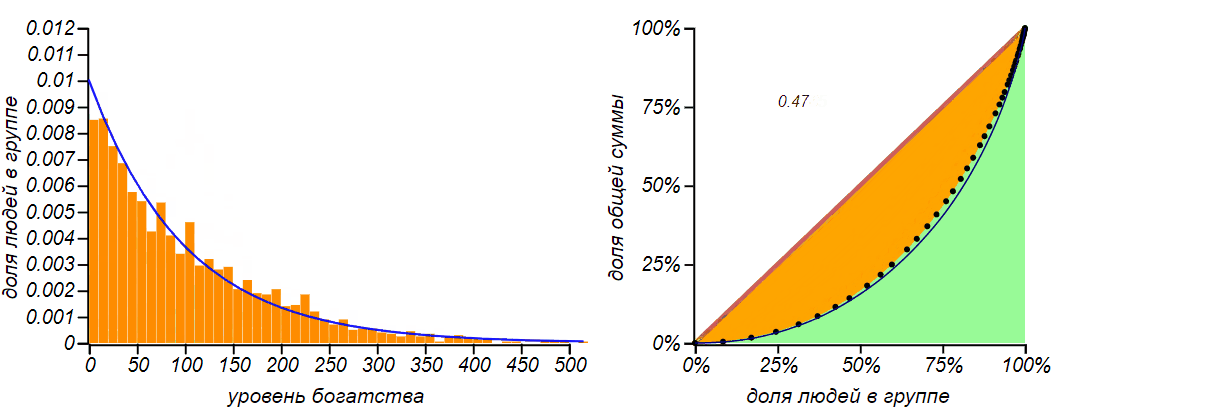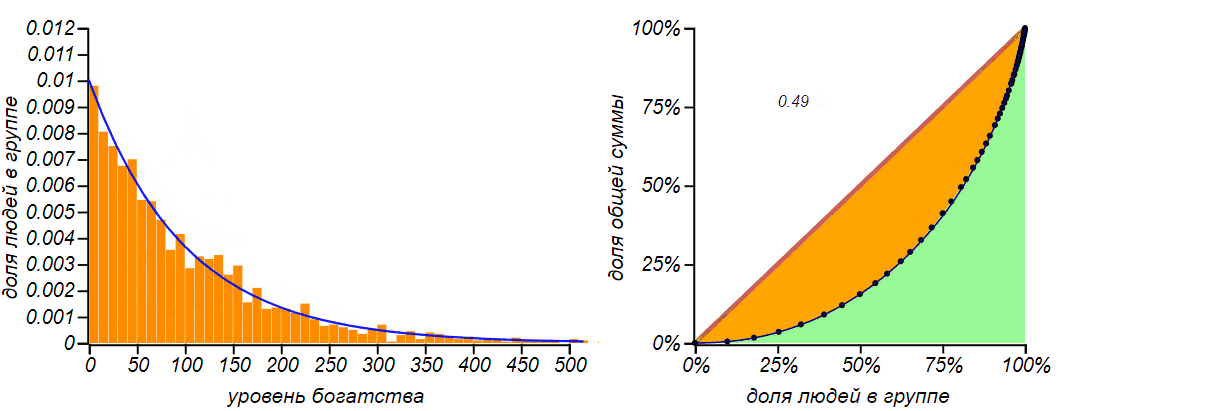
Результат имитационного моделирования для обмена равным количеством денег для $inline$ и $inline$ . Сначала, действительно, наблюдается явление, подобное диффузии, но по мере достижения функцией вероятности левой границы, распределение стремится к характерной несимметричной и не очень справедливой форме с коэффициентом Джини близкому к $inline$ .

Алгоритм обмена равными суммами

Исходные данные: xs — массив из n элементов, инициализированный значениями m.
Повторять
    i <- случайное целое от 0 до n
    если xs[i] > 0
        j <- случайное целое от 0 до n
        xs[i] <- xs[i] - 1
        xs[j] <- xs[j] + 1

Если эту книжку читает физик, то он сможет уверенно предположить что это может быть за распределение, он назовёт его распределением Гиббса. Внимательный читатель может вспомнить, что мы уже встречались с подобной картинкой и с таким индексом Джини, когда рассматривали фрустрацию во время ожидания автобуса. Тогда мы рассматривали распределение интервалов между пуассоновскими событиями, которое описывалось экспоненциальным распределением. Оба этих проницательных господина будут правы, называя разными именами одно и то же замечательно распределение.

Люди — молекулы

Распределение Гиббса — это из области статистической физики. Здесь описываются свойства систем, называемых красивым словом «ансамбль», которые состоят из великого множества взаимодействующих элементов, чаще всего, частиц. В ансамбле можно выделять произвольные подсистемы (например, отдельные частицы или их группы) и ставить им в соответствие некие функции состояния (это могут быть обобщённые координаты, скорости, концентрации, химические потенциалы и многое другое). С помощью методов статистической физики удаётся объяснить и вычислить параметры самых разнообразных явлений: химических и каталитических процессов, турбулентности, ферромагнетизма, поведения жидких кристаллов, сверхтекучести и сверхпроводимости и многих других.

Распределение Гиббса отвечает на вопрос: какова вероятность встретить некое состояние подсистемы, если даны а) энергия состояния, б) макроскопические (условно говоря, глобальные) свойства системы, такие, например, как температура и в) известно, что система находится в термодинамическом равновесии? Оно может быть схематично выражено следующим образом:

$p_{\mathrm{Gibbs}(T)}(x) = С e^{-\frac{E(x)}{kT}},$

где

$inline$ — некое состояние подсистемы,

$inline$ — энергия этого состояния,

$inline$ — абсолютная температура системы (или её аналог), а

$inline$ и

$inline$ — величины, необходимые для нормировки и соответствия размерностей. Условие равновесия очень важно, оно означает, что из рассмотрения исчезает время и что вся система окажется в наиболее вероятном своём состоянии для заданных условий.

Строгий вывод выражения для распределения Гиббса нам здесь не нужен, вместо него я хочу показать красивейшее чисто математическое рассуждение, приводящее к его экспоненциальной форме. Поскольку рассматриваются части системы, которые в сумме дают всю систему, то и в качестве их характеристики стоит выбрать какую-либо аддитивную величину, то есть такую, чтобы её значение для ансамбля было арифметической суммой значений его частей. В качестве такой величины в механике можно использовать энергию. С другой стороны, мы вычисляем вероятность наблюдать некоторое состояние системы, а вероятность величина мультипликативная, то есть, если систему можно разбить на части, то вероятность наблюдать все эти части одновременно будет равна произведению вероятностей для состояния каждой из частей. Таким образом, нам нужна функция, превращающая аддитивную величину в мультипликативную. Таким свойством обладает только показательная функция

$inline$ , сумму аргументов превращает в произведение значений:

$a^{x+y} = a^x a^y.$ Ну, а из всех показательных функций, наиболее удобной является экспонента, поскольку она очень хорошо ведёт себя при интегрировании и дифференцировании.

В нашей модели рынка мы имеем аддитивную величину — количество денег у каждого игрока, это аналог энергии. При описанном нами обмене, эта величина, как и энергия в физической системе, сохраняется. А какой смысл здесь у температуры? Это просто выяснить, посмотрев на выражение для плотности вероятности экспоненциального распределения:

$p_{\mathrm{Exp}(\lambda)}(x) = \lambda e^{-\lambda x},$

и вспомнив, что среднее значение для него равно

$1/\lambda$ . Так как число игроков в ходе торгов неизменно, то сохраняется и среднее арифметическое количество денег у игроков, равное первоначально раздаваемой сумме

$inline$ . Отсюда естественным образом следует, что

$\lambda = 1/m$ , значит в роли температуры в нашей экономической модели выступает среднее количество денег у игроков. В «разогретом» рынке с большой ликвидностью мы сможем наблюдать и больший разброс в уровне благосостояния, чем в «холодном», ведь в экспоненциальном распределении дисперсия равна

$1/\lambda^2$ . Как говорил Остап Бендер в «Золотом Телёнке» И. Ильфа и Е. Петрова: «Раз в стране бродят какие-то денежные знаки, то должны быть люди, у которых их много.»

Если быть совсем точным, и вспомнить, что деньги в нашем эксперименте это величина дискретная, то мы наблюдаем геометрическое распределение — дискретный аналог экспоненциального. Оно встречается в задаче подсчёта числа неудач до первого выигрыша при подбрасывании монеток разной степени честности. Эти два распределения подобны и становятся неотличимы при уменьшении вероятности выигрыша. В нашем эксперименте шансы получить рубль равны

$inline$ , это достаточно мало для того, чтобы называть распределение экспоненциальным.

Осталось разобраться с равновесностью итогового состояния рынка. Термодинамическое равновесие можно описать разными способами. Во-первых, равновесным должно быть стационарное состояние, в котором система может находиться неограниченно долго, не изменяя своих макроскопических параметров, и не образуя внутри себя упорядоченных потоков вещества и энергии. Во-вторых, оно должно быть устойчивым, то есть, если вывести систему из равновесия, она будет стремиться к нему вернуться. В-третьих, это наиболее вероятное состояние системы, чаще всего наблюдаемое, в которое со временем система будет стремиться попасть из любого другого, неравновесного. Наш эксперимент демонстрирует эти критерии равновесности: придя к экспоненциальному распределению, система в нём и остается, к тому же, в эксперименте легко убедиться, что из любого произвольного распределения мы, по истечении какого-то времени, снова придём к экспоненциальному. Но это ещё не доказательство, а только намёк, что мы, скорее всего, имеем дело с равновесием. Нужен какой-то формальный измеримый критерий, который однозначно указал бы нам, что система равновесна без необходимости ждать бесконечно долго или перебирать все возможные первоначальные распределения. Это был бы полезный критерий, который можно было бы применять и к реальному рынку, без необходимости проводить рискованные эксперименты на живых людях.

Дао выраженное словами — не истинное Дао

Размышления о равновесии привели физиков к понятию энтропии, которое постепенно вышло за пределы термодинамики и так понравилось ученым всех направлений, философам и широкой публике, что теперь энтропия получила ореол загадочности, непостижимости и бог знает ещё чего. Простое и специальное, в сущности, понятие приобрело в сознании широких масс репутацию необъяснимо управляющей миром концепции. Это связано с тем, что термодинамика — универсальная наука, описывающая на очень высоком уровне абстракции системы самой разнообразной природы: от физических, химических и биологических до социальных, экономических и даже чисто гуманитарных. После школьного курса, правда, остаётся ощущение, что термодинамика — это про скучный идеальный газ, какие-то поршни и невозможный цикл Карно. Такое весьма одностороннее представление связано с тем замечательным фактом, что термодинамика, будучи одной из самых абстрактных и универсальных разделов естествознания, элегантно решает прикладные задачи, понятные школьникам и полезные в промышленности. Этого не скажешь, например, о теории категорий или топологии — тоже весьма абстрактных, универсальных и, несомненно, полезных дисциплинах, но в повседневных задачах почти не встречающихся.

Итак, энтропия. Создателю термодинамики Клаузиусу, а позже Гиббсу и Больцману потребовалась количественная характеристика равновесности, говорящая о вероятности наблюдать указанное состояние системы или её частей. Причём, эта величина, отражающая вероятность, мультипликативную по своей природе, должна быть аддитивной функцией состояния, чтобы можно было бы вычислить её для системы, складывая значения, вычисленные для её частей. Когда мы искали подходящую функцию для распределения Гиббса, мы исходили из того, что она должна превращать аддитивный аргумент в мультипликативное значение. При поиске выражения для энтропии мы нуждаемся в функции, мультипликативной по аргументу и аддитивной по значению — это логарифмическая функция, обратная показательной. Энтропия состояния сложной системы может быть выражена как ожидаемое значение для логарифма вероятности наблюдения состояния всех её частей, или, по Больцману, как логарифм числа способов, которым можно реализовать это состояние системы. При этом более вероятному состоянию соответствует большее значение энтропии, а равновесному — максимальное из возможных.

Число способов реализовать то или иное состояние зависит и от числа ограничений или условий, при которых это состояние может реализоваться. Чем меньше таких ограничений, тем более вероятным является состояние и тем больше значение его энтропии. Эти ограничения и условия имеют смысл информации о состоянии. Отсюда возникла идея о том, что энтропия отражает степень нашего незнания о системе: чем меньше нам о состоянии известно, тем больше его энтропия. Позже Шеннон обобщил это понятие для любых систем, содержащих в себе информацию, в том числе и для распределений случайных величин. Вот что у него получилось: для случайной величины

$inline$ , определяемой функцией вероятности

$inline$ энтропия определяется следующим образом:

$H(X) \equiv -\mathrm{M}(\ln(p(x))) = -\sum{p(x)\ln(p(x))},$

где суммирование производится по всем значениям

$inline$ , в которых

$inline$ . Таким образом, мы имеем возможность вычислить энтропию состояния любой сложной системы, имея её статистическое описание.

Вот как изменяется энтропия по мере того как модель нашего рынка приходит к равновесию.

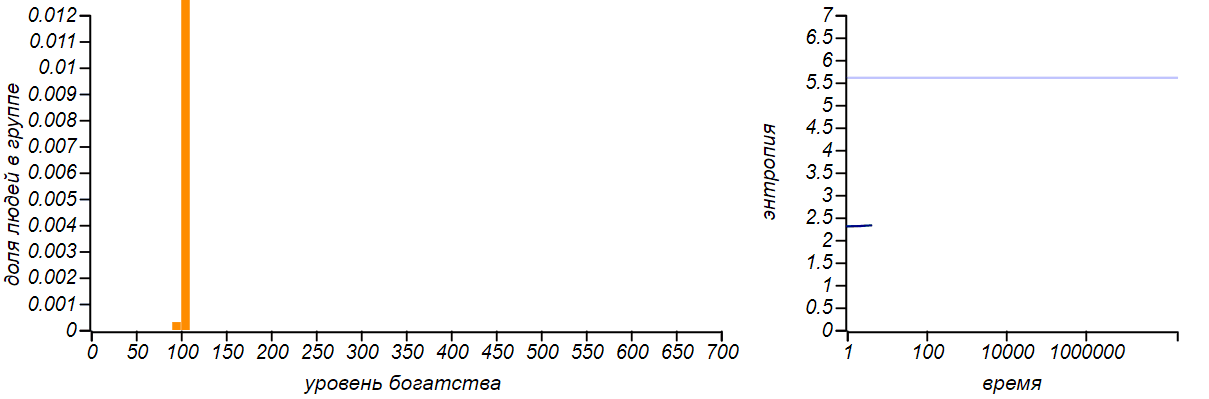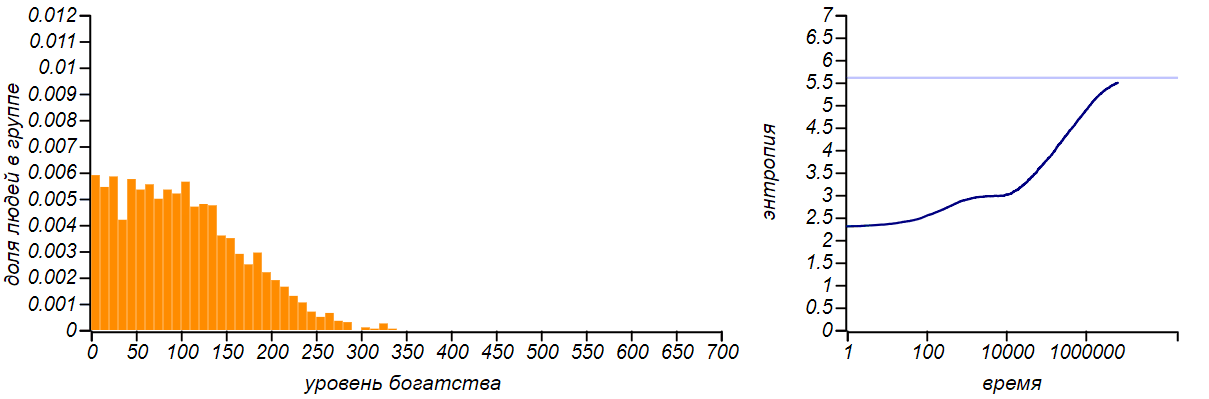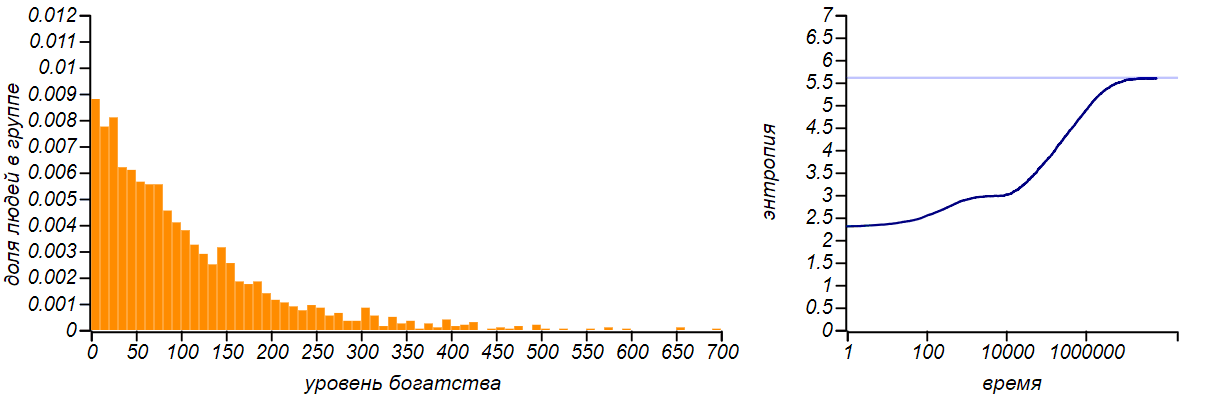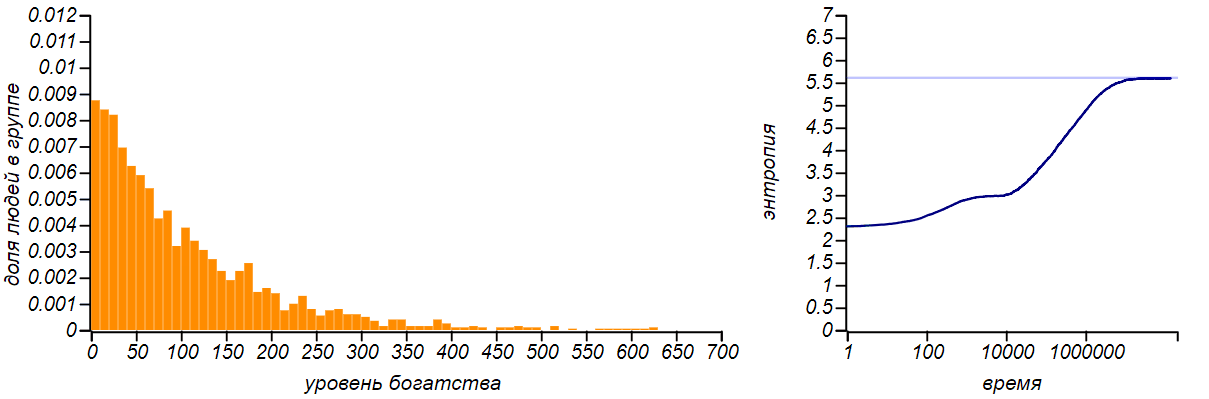
Рост энтропии по мере приближения рынка к равновесному состоянию. Горизонтальной линией на правом графике показано теоретическое значение энтропии для экспоненциального распределения, равное $1-\ln(\lambda)$ . Промежуточная «полочка» соответствует периоду, в течение которого распределение проходило стадию диффузии и было похоже на нормальное.

Таким образом, каждому распределению: задаваемому аналитически или полученному экспериментально в виде гистограммы, можно поставить в соответствие положительное число — его энтропию. Значит распределения можно сравнивать между собой, определяя более или менее равновесные и вероятные для заданных условий. Более того, для некоторого класса распределений можно выделить распределение с максимальной энтропией, причём, только одно. Классы определяются ограничениями, или мерой нашего знания о статистических свойствах системы. Приведём несколько примеров:

что нам известно о случайной величине $inline$	распределений с максимальной энтропией
$X\in[a,b]$	равномерное на отрезке $inline$
$X\in\{0,1\}$	распределение Бернулли
$X\in[0,\infty)$ + среднее	экспоненциальное, для дискретной величины — геометрическое
$X\in[x_m,\infty)$ + среднее геометрическое	распределение Парето (степенное)
$X\in[0,\infty)$ + среднее + среднее геометрическое	гамма-распределение
$X\in[0,\infty)$ + среднее геометрическое + дисперсия для среднего геометрического	лог-нормальное
$X\in(-\infty,\infty)$ + среднее + дисперсия	нормальное

Знакомые всё лица! Это очень часто используемые распределения, которые статистики применяют к широчайшему классу задач. Их универсальность обусловлена именно тем, что они, имея максимальную энтропию, наиболее вероятны и наблюдаемы. К ним, как к равновесным, стремятся многие распределения реальных случайных величин. Самым свободным от ограничений среди всех прочих является нормальное распределение: оно требует минимума информации о случайной величине. Меньше уже не получится: если мы укажем лишь среднее значение, то стремясь увеличить энтропию, распределение «размажется» по всей числовой оси. Зато, если мы знаем лишь среднее значение, но при этом ограничим случайную величину положительными значениями, то равновесное распределение будет однозначным — экспоненциальным. Именно этот случай мы и наблюдали в нашем эксперименте с рынком. Нам заранее было известно лишь сколько денег мы выдали каждому игроку и то, что количество денег в системе неизменно, это фиксировало среднее значение. А так как деньги у нас величина положительная, вероятнее всего, в равновесии мы получим экспоненциальное распределение богатства с индексом Джини равным

$inline$ .

Существует множество модификаций описанной нами модели: обмен может происходить не одним рублём, а случайной величиной, ограниченной состоянием дающего, при этом можно давать деньги не какому-то одному игроку, а распределять случайным образом. Пока мы не вводим в игру новых параметров все эти модификации не меняют форму равновесного распределения богатства — оно остаётся экспоненциальным. В этом можно убедиться с помощью имитационного моделирования, но приводить картинки для различных способов обмена не интересно — они все одинаковы. Многие исследователи отмечали эту особенность моделей рынка. Интересна модель построенная Драгулеску и Яковенко из Мерилендского университета, в которой игроков объединяют в некие компании и далее имитируется взаимодействие компаний с игроками-работниками и игроками-покупателями. Но и в этом сложном случае равновесным является экспоненциальное распределение, безразличное к выбираемым параметрам модели.

Чтобы продемонстрировать универсальность принципа максимума энтропии давайте искусственно ограничим сверху уровень богатства отдельного игрока, запретив ему получать деньги, если у него уже есть некая фиксированная сумма. Равновесное распределение, конечно же, изменится. А в случае, если правая граница будет равна удвоенному среднему значению, то мы приходим к случаю, описанному в первом ряду таблицы. Действительно, ограничивая случайную величину конечным отрезком и не указывая больше ничего, мы не можем предположить никакого другого ожидаемого значения среднего, кроме середины этого отрезка. Следовательно, равновесным распределением при таком варианте должно быть равномерное. Давайте проверим, так ли это?

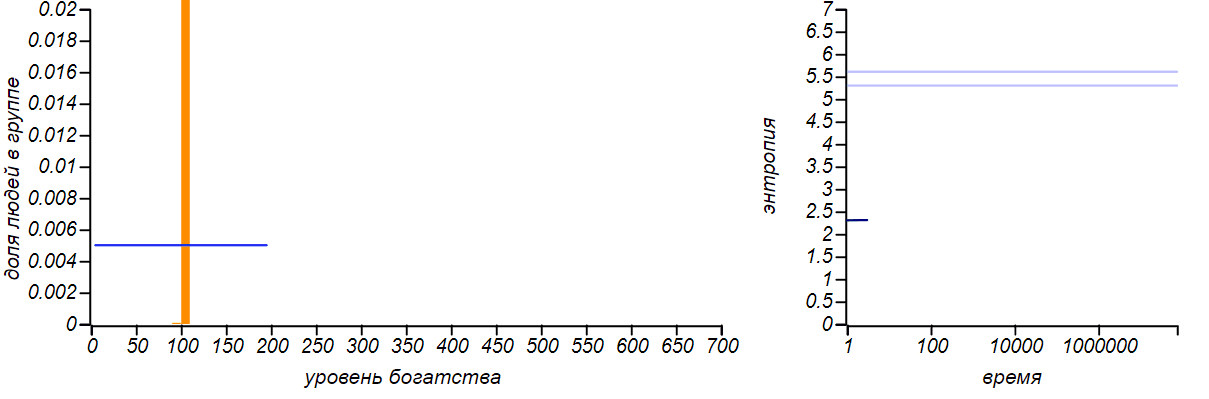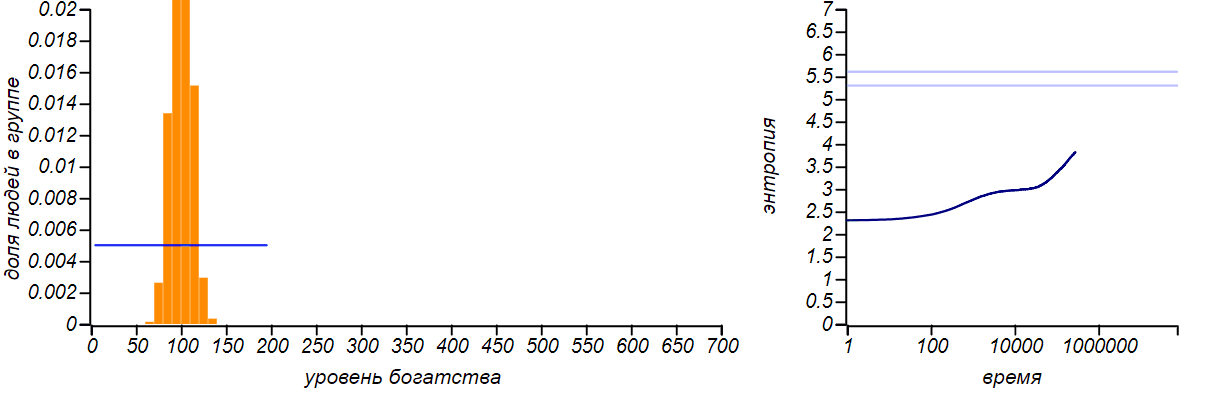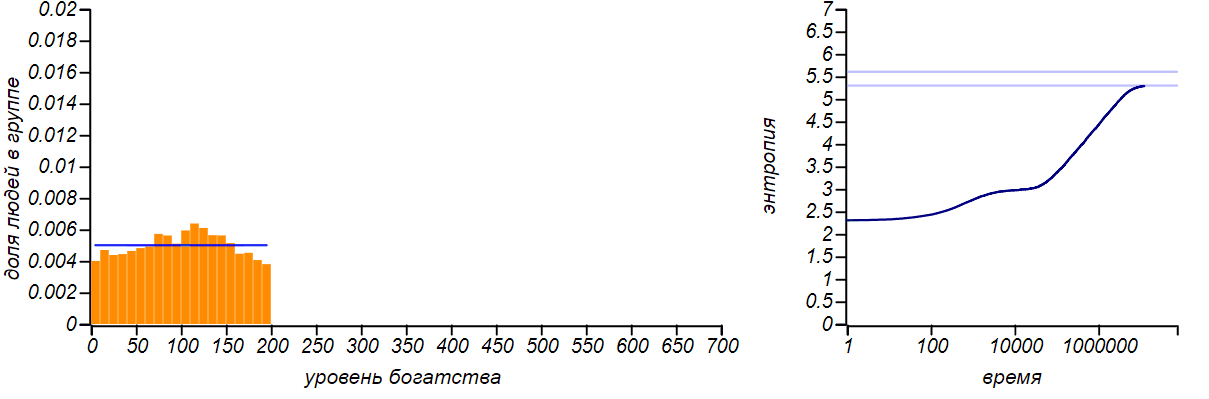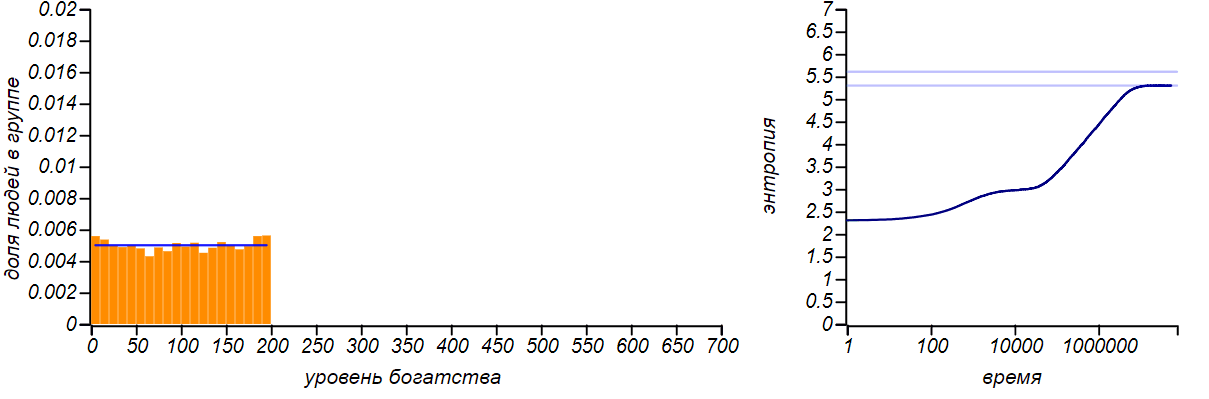
Вот что происходит при ограничении сверху возможного уровня богатства игроков, причём, таким образом, что верхняя граница ровно вдвое превышает среднее значение. Согласно принципу максимальной энтропии, равновесным распределением должно быть равномерное. Горизонтальной линией на правом графике показано теоретическое значение энтропии для равномерного распределения.

Алгоритм обмена равными суммами с ограничением сверху

Исходные данные: xs — массив из n элементов, инициализированный значениями m, xMax — максимальная разрешённая сумма.
Повторять
    i <- случайное целое от 0 до n
    если xs[i] > 0
        j <- случайное целое от 0 до n
        если xs[j] < xMax
            xs[i] <- xs[i] - 1
            xs[j] <- xs[j] + 1

А что будет при нарушении симметрии, то есть, если мы сдвинем правую границу вправо или влево?

<\br>

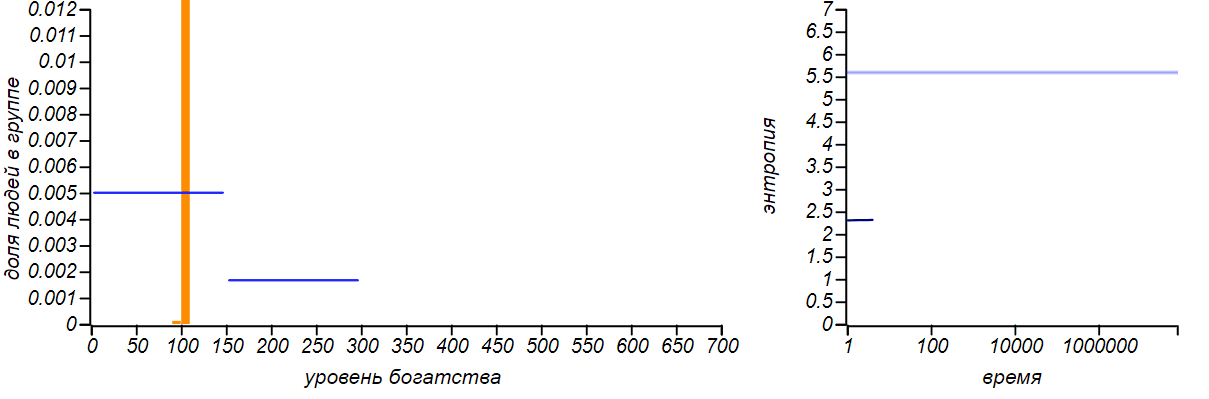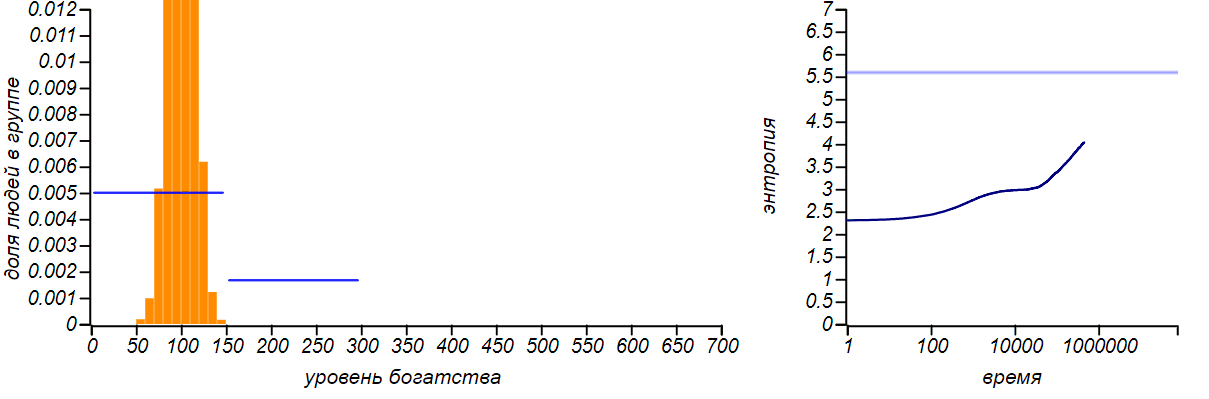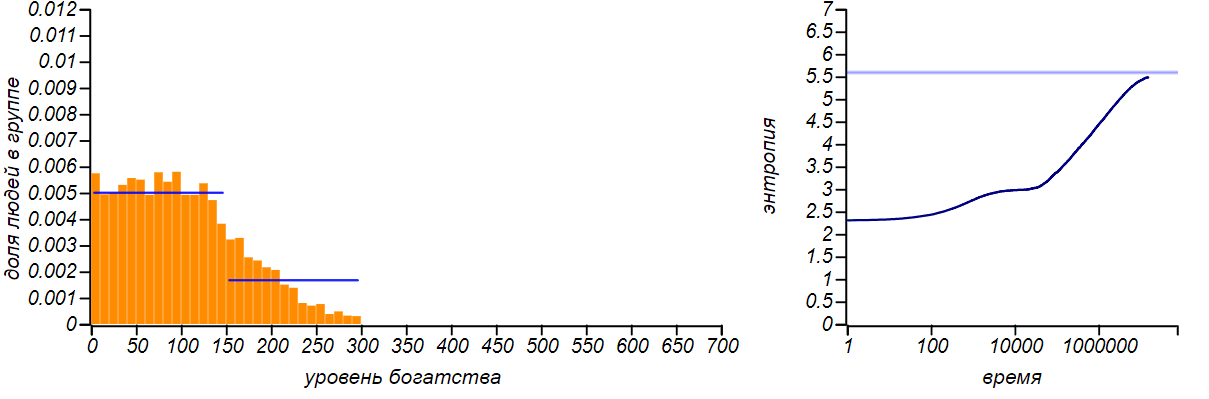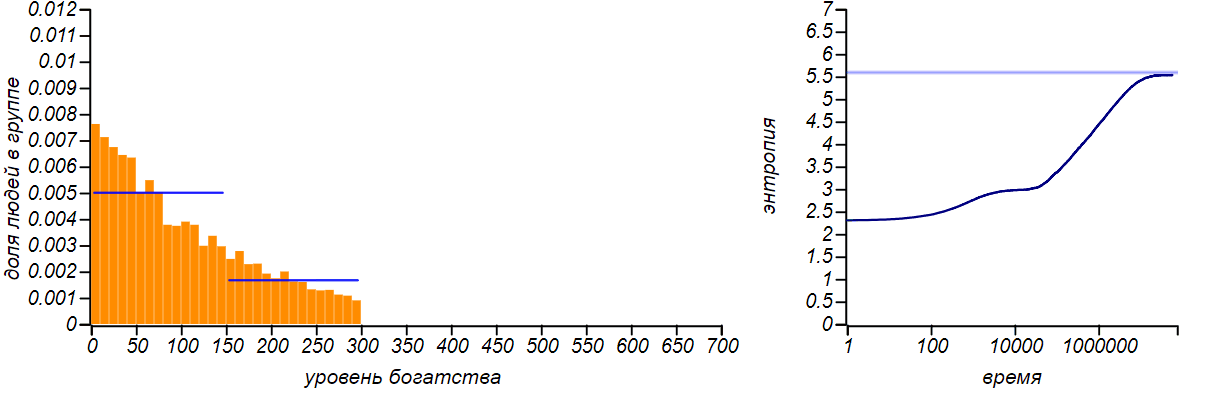
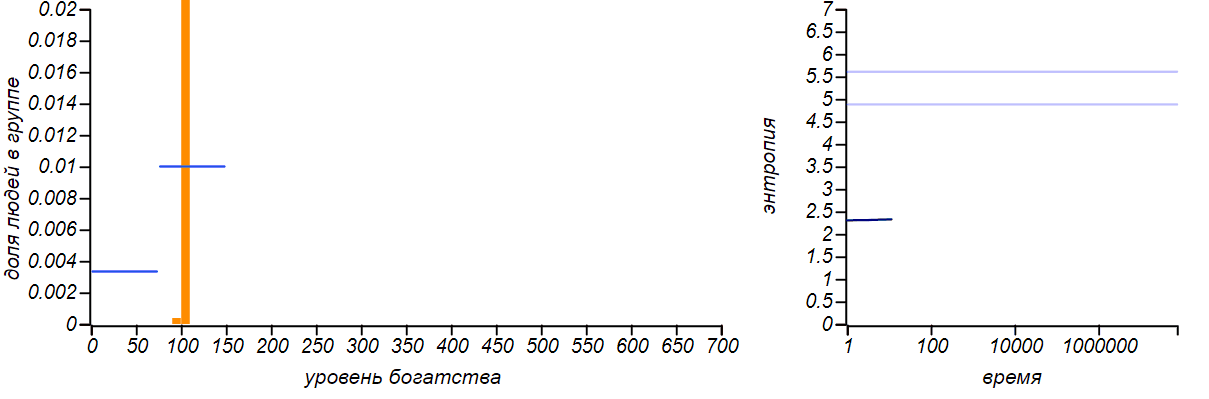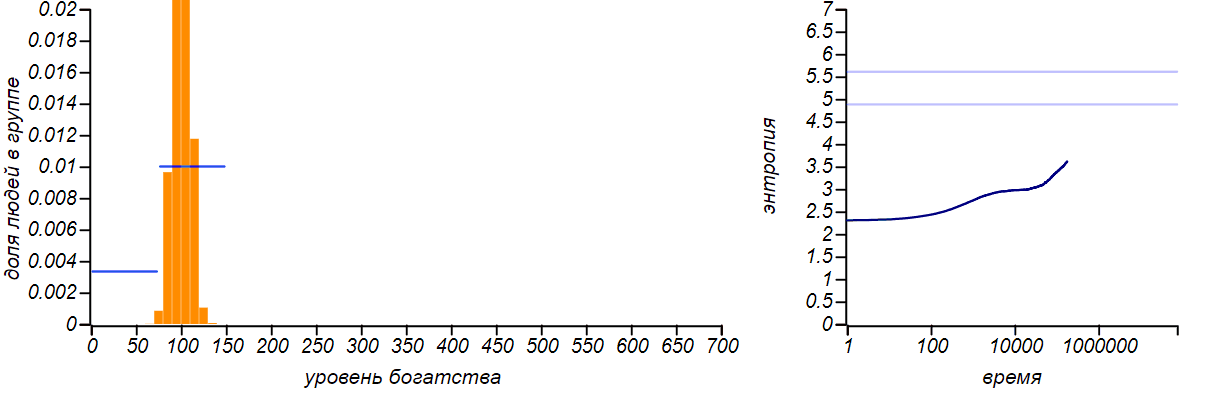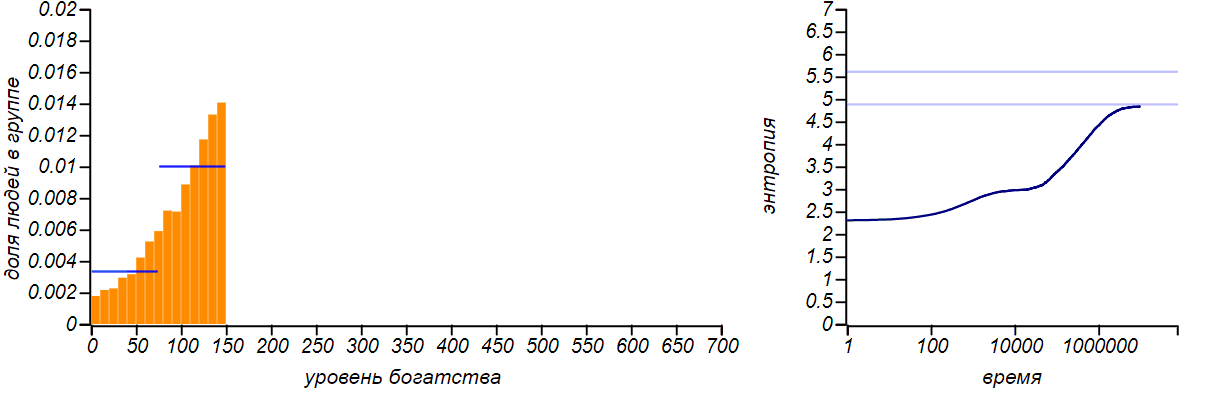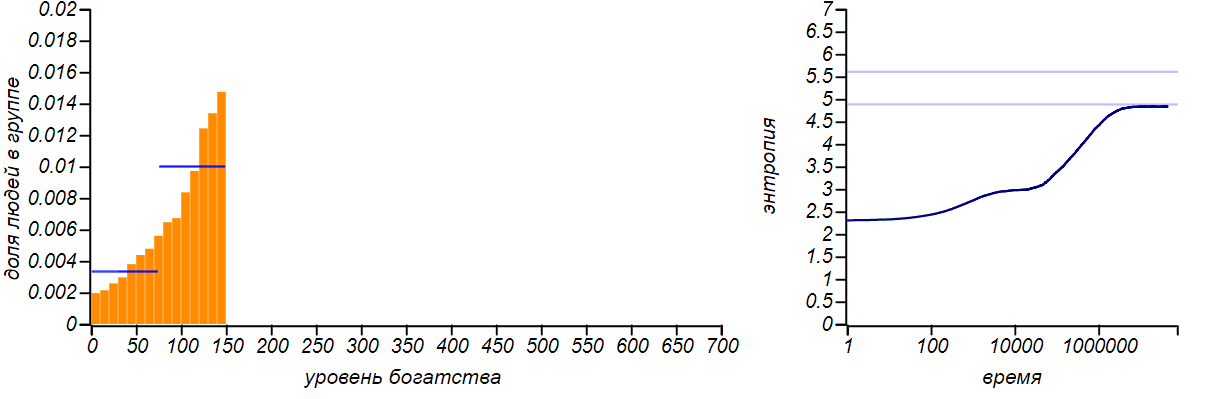
Варианты несимметричных ограниченных распределений в сравнении с распределениями Бернулли, соответствующими смещению среднего значения. Горизонтальные линии на графиках энтропии указывают теоретические значения для энтропии распределений Бернулли.

Распределение достатка перестало быть равномерным, приобретя форму ограниченного экспоненциального. При смещении правой границы влево в равновесии богатых игроков стало больше, чем бедных. Если мы «загрубим» гистограмму, оставив лишь два столбца, то получим распределение Бернулли, показывающее какова вероятность оказаться условно «бедным» или «богатым». Когда значения случайной величины ограничены всего двумя значениями, распределение Бернулли — единственный выбор, он же, естественно, доставляет максимум энтропии. Но обратите внимание на то, что энтропия наших модельных распределений стремится именно к тем значениям, которые предсказываются распределением Бернулли. Коэффициенты Джини для двух этих случаев равны

$inline$ и

$inline$ , соответственно.

Загадочная и могущественная энтропия — это, конечно, круто и, возможно, даже убедительно. Но почему же при симметричном обмене, бедных становится больше, чем богатых? Почему мода равновесного распределения равна нулю? Надо, как говорят физики, разобраться в кинетике процесса, то есть в судьбе отдельных частиц. Мы не ошиблись, предположив, что модель случайного блуждания описывает изменение состояния отдельного участника торгов: он с равной вероятностью совершает шаги как вверх, так и вниз. А для случайного блуждания выполняется один знаменитый закон подлости: проклятие игрока. Напомню, что он состоит в том, что при достаточно долгом наблюдении, случайно блуждающая частица обязательно окажется в любом наперёд указанном месте. Причём расстояние на которое частица удалится от какой-либо начальной точки пропорционально квадратному корню от числа шагов. Всё это приводит к тому, что если частица начинает свой путь вблизи нуля, то она с высокой вероятностью его достигнет, а так как ноль в нашей задаче — это непроницаемая граница, то она будет вынуждена вновь и вновь начинать свой путь около нулевой точки, испытывая пресловутое проклятие. По мере удаления частицы от нуля, вероятность к нему вернуться уменьшается и у богатых становится больше шансов сберечь своё состояние. Но тогда что же мешает частице удалиться сколь угодно далеко, а конкретному игроку стать сколь угодно богатым? Вообще-то, ничего, кроме конечности денег в системе — экспоненциальное распределение отлично от нуля на всей положительной полуоси. Но для того чтобы достичь невероятного богатства по правилам нашей игры нужно чтобы все игроки случайно выбирали одного и того же игрока раз за разом. И в первый-то раз вероятность такого выбора составляет

$(1/n)^{n-1}$ — одна миллиардная для группы из десяти человек, а уж случайно повторить это много раз и вовсе невероятно. Выбор кому отдать деньги в нашей модели падает на всех одинаково, а это значит, что доставаться он будет не только богатым, но и бедным. Есть в этом мире справедливость! Хоть и торжествующая недолго, если ты не богат.

Экономика должна быть экономной

Покуда наша модель обмена никак не учитывает достатка игроков, она остаётся нереалистичной. В действительности, богатые тратят больше, а бедные меньше, более того, разумные люди стараются сохранить какую-то часть своего состояния. В качестве следующего усложнения модели, давайте потребуем, чтобы игроки при обмене отдавали некую известную долю

$\alpha$ своего состояния. В систему вводится новый параметр и новое ограничение, следовательно, равновесное состояние может отклониться от экспоненциального. Оперируя долями от уровня благосостояния, мы переходим к мультипликативным характеристикам, таким, например, как доходность вложения, возврат инвестиций и т.д. Во всех учебниках по экономике указывается, что если вы желаете вычислить среднюю доходность вложения, скажем, за много лет, следует вычислять среднее геометрическое для доходностей каждого года. В нашем случае среднее геометрическое однозначно, хоть и нетривиально, определяется значением

$\alpha$ . Таким образом, добавляя новый параметр мы фиксируем среднее геометрическое распределения дохода игроков, или среднюю доходность модели рынка. Значит, мы можем ожидать, что равновесное распределение богатства должно неплохо описываться гамма-распределением. В этом мы можем убедиться, проведя имитационное моделирование.

Если расходы при обмене пропорциональны достатку равновесное распределение стремится к характерному несиметричному колоколообразному гамма-распределению. В данной модели $\alpha = 1/3$ . Средняя доходность обмена составила $75\%$ .

Алгоритм пропорционального обмена

Исходные данные: xs — массив из n элементов, инициализированный значениями m, alpha — доля капитала, которая тратится при обмене.
повторять
    i <- случайное целое от 0 до n
    если xs[i] > 0
        dx <- floor(xs[i]*alpha)
        xs[i] <- xs[i] - dx
        j <- случайное целое от 0 до n
        xs[j] <- xs[j] + dx

Уменьшение доли бедняков связано с тем, что они тратят в среднем меньше, чем получают от богатых, ведь и те и другие обмениваются долями своего капитала. Но этот социальный лифт действует только при

$\alpha< 1/2$ . Если тратить больше половины того, что имеешь, вероятность оказаться в бедняках становится весьма ощутимой. Для различных значений

$\alpha$ можно получить весьма различающиеся по форме распределения с широким диапазоном несправедливости:

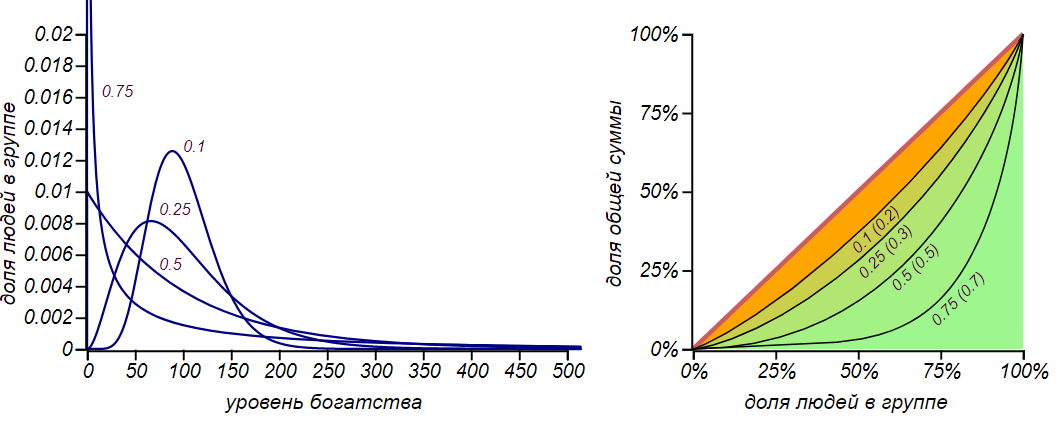
Различные варианты равновесных распределений при расходах, пропорциональных достатку. Графики помечены значениями $\alpha$ , а на правом графике в скобках приведены ещё и значения индекса Джини.

Точное решение

Эта книжка, хоть и популярная, но математическая. Это значит, что все математические результаты, попавшие на её страницы, имеют доказательства или строгий вывод, пусть, зачастую, остающиеся и за пределами изложения ввиду их громоздкости. И хотя для дальнейшего изложения этот результат не нужен, я приведу точное, и довольно изящное выражение для распределения, которое удалось получить для модели пропорционального обмена.

Гамма-распределение

$\mathrm{Gamma}(k,\theta)$ — это двухпараметрическое распределение, которое часто используется, как обобщение экспоненциального и сводится к нему при

$inline$ . Оно имеет ряд замечательных свойств, делающих его полезным. Об одном из них, мы уже говорили — это распределение с максимальной энтропией в своём классе. Другое важное свойство — бесконечная делимость, то есть гамма-распределение можно получить, как сумму случайных величин, тоже подчиняющихся гамма-распределению. Конкретнее,

$X \sim\mathrm{Gamma}(k_1,\theta), Y \sim\mathrm{Gamma}(k_2,\theta) \implies X+Y\sim\mathrm{Gamma}(k_1+k_2,\theta)$

Наконец, это распределение масштабируемо:

$X \sim\mathrm{Gamma}(k,\theta) \implies a X \sim\mathrm{Gamma}(k,a \theta).$

Эти свойства позволили получить распределение благосостояния для нашей модели со средним значением

$inline$ и коэффициентом

$\alpha$ :

$\mathrm{Gamma}\left(\frac{1}{\alpha}-1, \frac{1}{m}\left(\frac{1}{\alpha}-1\right)\right)$ .

Видно, что чем большую часть своего капитала игроки вынуждены тратить (например, на повседневные нужды или еду), тем больше становится доля бедных и тем менее справедливым становится общество. Любопытно, что при

$\alpha=1/2$ равновесное распределение становится экспоненциальным, как в модели при равном обмене. Экспоненциальное распределение является частным случаем гамма-распределения, так что это превращение, само по себе, неудивительно. Но тут есть одна любопытная тонкость: энтропия этого частного случая больше чем энтропия распределений с любыми другими значениями

$\alpha$ . Посмотрите, как изменяется энтропия по мере развития ситуации при

$\alpha=0.75$ :

В процессе перехода к равновесию, система «проскакивает» состояние с максимальной энтропией.

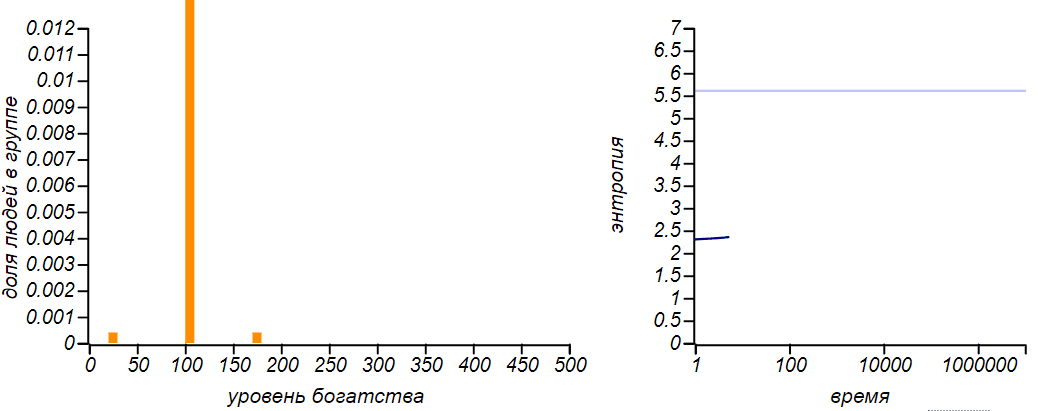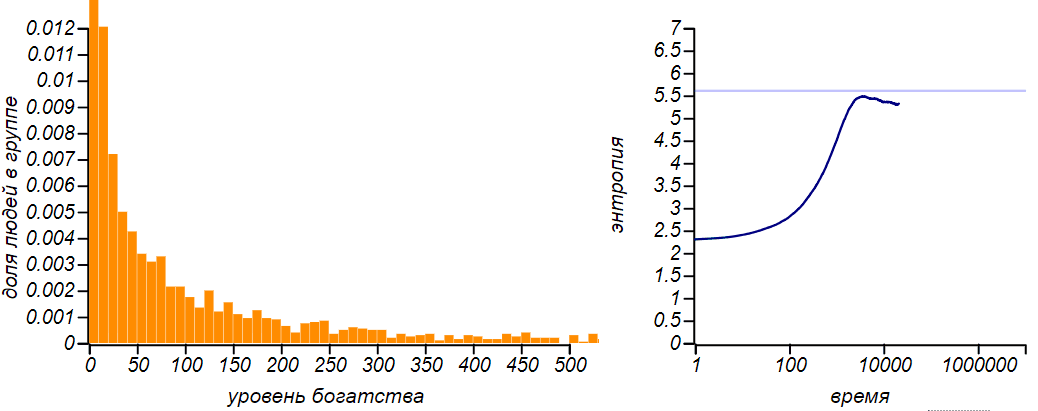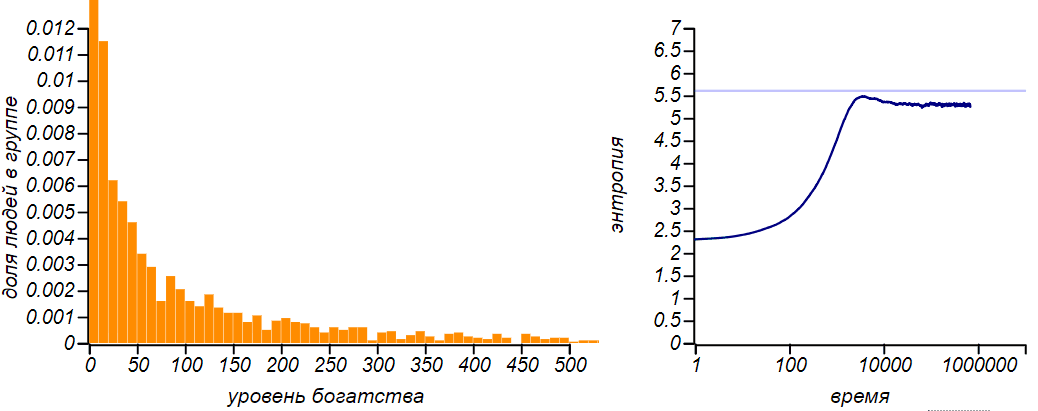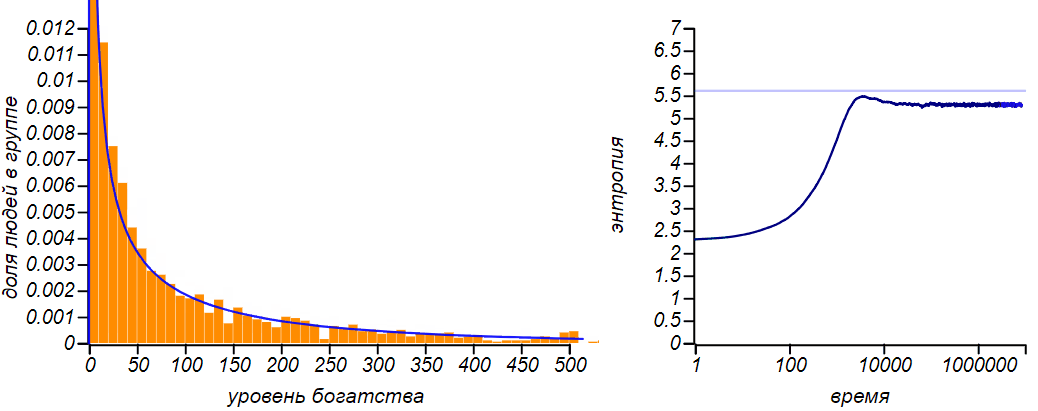
Сначала значение энтропии монотонно увеличивается, потом, немного не достигая теоретического максимума, соответствующего экспоненциальному распределению, останавливается и начинает уменьшаться. Нет ли в этом противоречия с определением равновесного состояния, как состояния с максимумом энтропии? Противоречия нет, поскольку равновесное состояние должно быть стационарным, то есть не создающим направленных потоков энергии и устойчивым, или, говоря языком теории динамических систем, притягивающим к себе систему. И из всех стационарных равновесным будет состояние с максимальной энтропией. А в нашем случае

$\alpha = 0.75$ , экспоненциальное распределение соответствует нестационарному состоянию.

Исследователи из Бостонского университета Исполатов и Крапивский усложнили модель пропорционального обмена таким образом, что обмен происходит с учётом не только благосостояния тратящего, но и получающего. Миллионер редко покупает что-либо у зеленщика, и зеленщик нечасто имеет большой доход, с другой стороны, производитель автомобилей экстра класса будет взаимодействовать лишь с богатыми клиентами, но и сам останется не в накладе. И вот, в моделях, в которых богатые начинают платить преимущественно богатым, а бедные — бедным, общество разваливается окончательно.

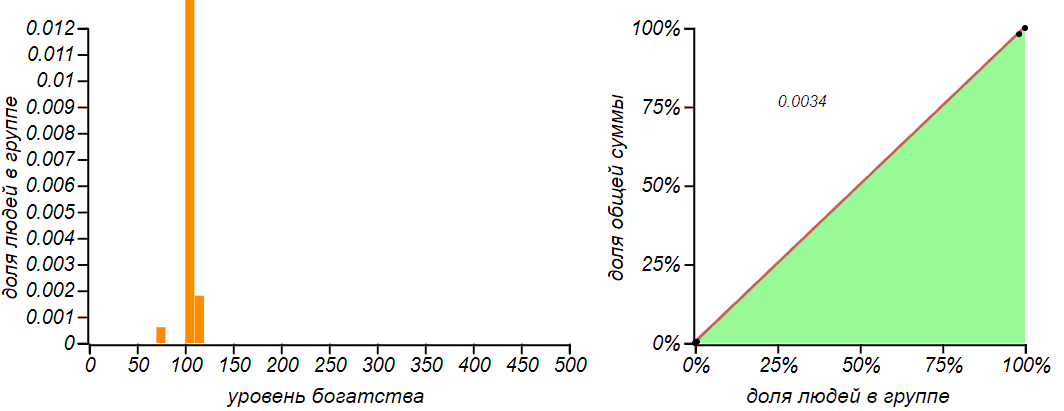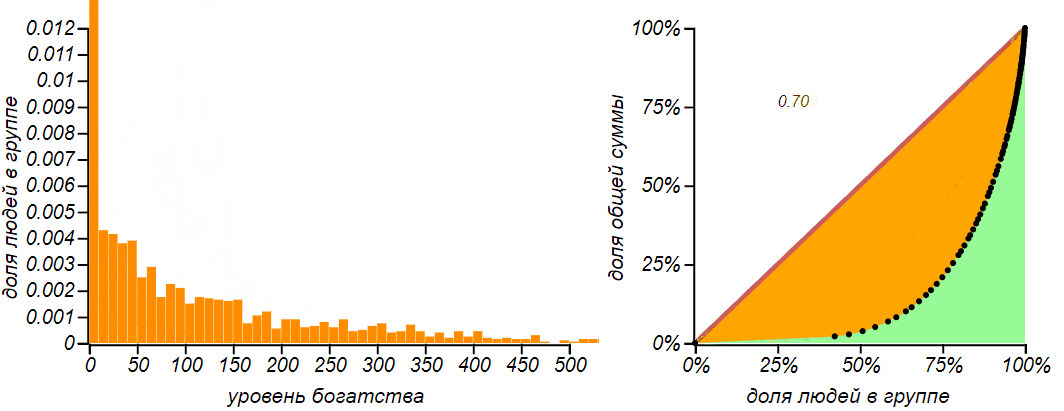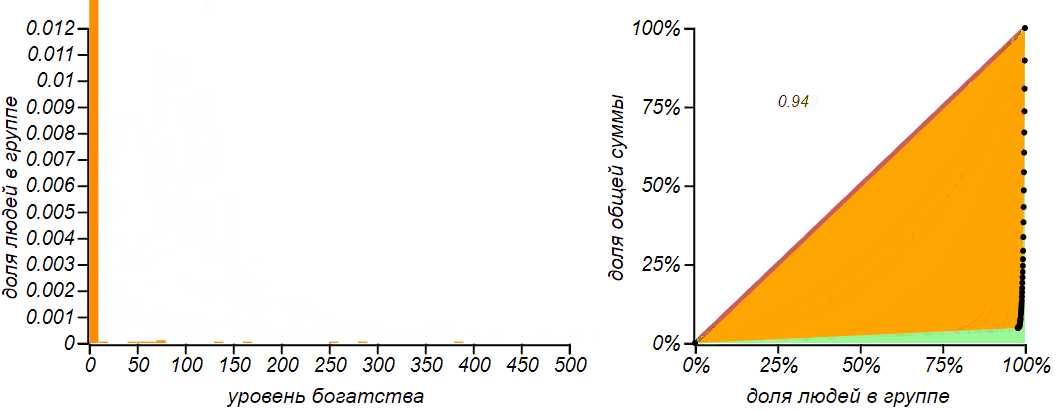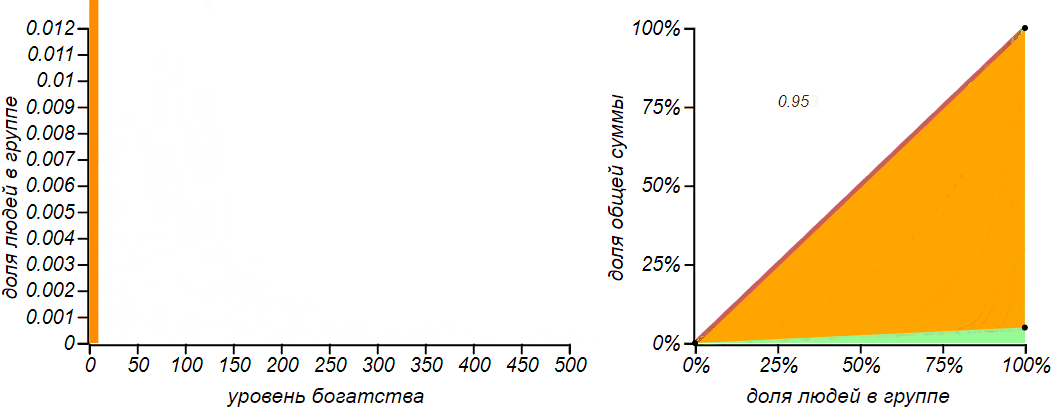
Если денежные потоки становятся зависимы от капитала, система теряет устойчивость и приводит к постоянному обнищанию группы и нарастанию классового неравенства. В этом примере $\alpha = 0.3, \beta = 0.1$ (см. алгоритм внизу).

Алгоритм пропорционального обмена Исполатова-Крапивского

Исходные данные: xs — массив из n элементов, инициализированный значениями m, alpha — доля капитала, которая тратится при обмене, beta — доля капитала, приобретаемого при обмене.
повторять
    i <- случайное целое от 0 до n
    если xs[i] > 0
        dx <- floor(xs[i]*alpha)
        xs[i] <- xs[i] - dx
        повторять пока dx > 0
            j <- случайное целое от 0 до n
            d = min(dx, floor(xs[j]*beta))
            xs[j] <- xs[j] + d
            dx <- dx - d

В этой системе существует только одно стационарное состояние: когда все игроки не имеют (и следовательно не получают) ровным счётом ничего, а всё богатство достаётся кому-нибудь одному. Коэффициент Джини в таком состоянии практически равен единице, и оно очень далеко от нормального равновесного — его энтропия почти равна нулю. Спасти положение может ограничение снизу, запрещающее игрокам терять абсолютно все сбережения, и в этом случае равновесное распределение становится снова экспоненциальным либо гамма-образным. Можно также ввести ограничение сверху — тогда мы получим некое несимметричное распределение, соответствующее распределению Бернулли. Модель такого дикого рынка вполне применима к рынку ценных бумаг без каких-либо ограничений, но на реальных биржах с этим борются, вводя ограничения на объем сделок, совершаемых за день и на максимальные уровни роста или падения цены на тот или иной актив.

Всё это печальные выводы, говорящие не в пользу свободного рынка, то ли дело, модель, предложенная Шариковым! А какова же энтропия у вырожденного распределения? Согласно стандартной формуле, она в точности равна нулю. Это самое неравновесное, самое маловероятное распределение, и в любой модели обмена оно нестационарно, так что получить подобное общество можно только искусственно. Дикий рынок, конечно, не подарок — он неустойчив и тяготеет к вопиющему неравенству. Требуется множество взаимосогласованных ограничений и тонко настроенных связей для построения устойчивого рынка и более или менее справедливого общества. Человечество исследует этот вопрос ещё не очень долго и в основном, на ощупь, методом проб и ошибок, но одно ясно: несправедливость в экономическом пространстве — не следствие поганой человеческой натуры, а объективное свойство системы, частью которой мы все являемся. Более того, попытки создать абсолютную справедливость по-шариковски всегда проходили с с боем и кровью, а результаты, в силу её неравновесности, существовали недолго.

Вряд ли молекулы и атомы рассуждают о несправедливости своего мира, да и физики с инженерами за двести лет смирились с тем, что какую бы идеальную тепловую машину они не построили, хаос не позволит преобразовать тепло в работу больше положенной доли. Когда понятно, то не так обидно. Надеюсь, эта глава поможет любопытному читателю понять и принять наш сложный несправедливый мир.

Комментарии (106)

Fracta1L
14.10.2018 13:58
#19233821
Как я понял, суть такова: как «справедливо» ни дели деньги между всеми, спустя некоторое время всё вернётся на круги своя.
1. DGN
  14.10.2018 17:47
  #19234423
  Да уж, какой то закон обратный термодинамике…
1. samsergey Автор
  14.10.2018 23:53
  #19235293
  Есть варианты с налогами и сборами, которые неплохо работают, до тех пор, пока люди подчиняются алгоритму. Но люди выше этого и начинают мухлевать. Так что да, все возвращается на круги своя :)
1. riky
  15.10.2018 00:22
  #19235333
  да, пока есть корпорации в которых маленькая кучка людей получает сверхдоходы, а все остальные сводят концы с концами на их фоне — так и будет.
  
  Когда нибудь люди начнут самоорганизовывать производство и управление будет происходить снизу всеми участниками. При этом главная цель не максимизация прибыли, а максимизация пользы для общества. При этом происходит справедливое распределение благ (не путать с равным) минимизация вреда экологии, увеличение удовлетворения от жизни.
  
  но конечно до этого нужно еще дойти.
  1. Fracta1L
    15.10.2018 08:58
    #19235851
    +1
    управление будет происходить снизу всеми участниками
    
    Поломойка, управляющая корпорацией? Лолище.
    
    При этом главная цель не максимизация прибыли, а максимизация пользы для общества
    
    Ясно: будет ни прибыли, ни пользы.
    
    Некоторых людей история ничему не учит.
    
    riky
    15.10.2018 11:42
    #19236655
    Поломойка там будет явно не в одиночку, она будет голосовать вместе с еще миллионом других жителей. Во вторых для этого изначально нужен равный доступ всех к информации, чтобы люди могли адекватно оценивать обстановку, сейчас люди живут в искусственно созданной информационной среде.
    
    Fracta1L
    15.10.2018 12:00
    #19236743
    +1
    она будет голосовать вместе с еще миллионом других жителей
    
    На голосовании о бюджете на следующий год победил вариант «взять всё и поделить на всех»
    
    Во вторых для этого изначально нужен равный доступ всех к информации, чтобы люди могли адекватно оценивать обстановку, сейчас люди живут в искусственно созданной информационной среде
    
    Да, точно. Это не люди предпочитают смотреть Рен-ТВ и читать посты в Одноклассниках, это коварные капиталисты их дезинформируют. Только когда я ищу и скачиваю с открытых публичных сайтов специализированные труды с ценнейшей информацией, там счётчики скачиваний редко достигают 5 разрядов, обычно это единичные сотни-тысячи скачиваний.
    
    К тому же, мало иметь релевантную инфу, нужно уметь с нею работать, а у многих людей с банальной логикой проблемы. Я уж не говорю про какое-то экономическое мышление. У людей взять бешеный кредит под конские проценты для того, чтобы купить барахло — считается нормой, а не безумием.
    
    А вообще, я не понимаю, почему разделение труда вдруг должно перестать действовать в такой специфической области, как управление. Да и сомневаюсь я, что полотёрка захочет забивать себе голову этими цифрами да графиками. Если бы она этого хотела, она бы пошла выучилась на экономиста или буха, и работала бы уже не полотёркой.
    
    riky
    16.10.2018 14:21
    #19241989
    Всё так, но вы оцениваете людей которые являются продуктом современной системы (политической/экономической/социальной и тд). Это очень специфический продукт и по большому счету это уже брак. В другой суперпозиции этих полей создается другой продукт, взгляните хотя бы на людей в разных странах. Вроде везде одинаковые люди с двумя руками и ногами, а ведут себя довольно таки по-разному.
    
    На данный момент миром правят маркетологи, они создают тенденции чтобы люди потом хотели «взять бешеный кредит под конские проценты для того, чтобы купить барахло». У обычных людей как правило просто нет времени чтобы остановится и оглянуться, правильно ли я живу. Их информационное поле на 99% забито той самой ерундой о которой вы говорите, и люди начинают думать что это и есть важно. Например, как вы думаете, если бы по телику 90% времени показывали классическую музыку люди были бы такими же?
    
    Человечество в целом развивается, поколения сменяются. Да и в будущем нам обещают полную тотальную автоматизацию, так что полотерке в любом случае нужно будет поискать более творческое занятие, которое роботы не смогут делать.
    
    И 2) люди стремятся не к равенству, а к справедливости. Взять все и поделить поровну хотят лишь тунеядцы которые ничего не хотят делать, а получать хотят как у всех.
    
    riky
    16.10.2018 14:24
    #19242019
    дополнение по 2) habr.com/post/424071/?reply_to=19238387#comment_19242017
    
    Fracta1L
    16.10.2018 14:37
    #19242089
    Например, как вы думаете, если бы по телику 90% времени показывали классическую музыку люди были бы такими же?
    
    В СССР по телеку и в прочих СМИ превозносили скромность и аскетичность, клеймили буржуазное потребительство и прочее моральное разложение, но люди всё равно мечтали о квартирах-машинах-дачах, модных шмотках, чешских стенках и прочих атрибутах достатка и социального статуса.
    
    Все эти офигительные истории про то, как маркетологи правят миром, рассказывают те, кто в маркетинге не работал никогда. Тем более, что информационное поле очень разнородно, и на сотню хвалебных историй в адрес вещизма приходится сотня же увлекательных рассказов в адрес принципа «нафиг тебе этот статусный хлам, собирай эмоции и впечатления, даже из простых вещей можно получить море удовольствия!»
    
    Mike_soft
    16.10.2018 14:54
    #19242191
    +1
    … и каждый день в 23:15 показывали концерт классической музыки. рекламы по телевизору не было вообще. в газетах рекламировали маргарин (ибо с маслом были проблемы)…
    
    mkshma
    15.10.2018 14:29
    #19237309
    -1
    Поломойка там будет явно не в одиночку, она будет голосовать вместе с еще миллионом других жителей.
    
    Казалось бы выборы в ограны госуправления в огромном количестве стран уже должны были научить людей тому простому факту, что обычным людям нельзя позволять принимать такие решения. Они импульсивны, они глупы, они ведутся на популизм, они готовы тешить свое эго в ущерб уровню жизни. Условных «поломоек» наоборот надо всячески ограждать от выборов любого толка.
    
    2PAE
    15.10.2018 12:31
    #19236853
    -1
    Поломойка, управляющая корпорацией? Лолище.
    
    Россия живёт по такому принципу и что вам не так?
    Или вы не считаете Россию великой державой и первой странной в мире?
    
    Mike_soft
    16.10.2018 07:34
    #19239929
    «первой странной»? Да, странностей у нас предостаточно…
  1. Taliesien
    15.10.2018 17:55
    #19238387
    +1
    Даже если чисто гипотетически допустить, что люди придумают решение как разделить деньги между всеми поровну, чтоб никто не был обижен. Через некоторое время найдется, другой способ обозначить неравенство. Люди так устроены, что всегда кто-то должен быть «ровнее» других. А деньги это просто очень удобный и доступный инструмент измерения социального неравенства. Это, грубо говоря, не причина неравенства, а следствие. А причина в наших базовых животных инстинктах.
    
    Mike_soft
    16.10.2018 07:40
    #19239943
    +2
    Собственно, в СССР при «почти равных» денежных доходах (разрыв был, но гораздо меньше, чем сейчас) для «более равных» были «спецмагазины», «спецбуфеты», санатории и больницы…
    
    Fracta1L
    16.10.2018 07:40
    #19239947
    +1
    Причина не в каких-то ужасных-отвратительных инстинктах, а в том, что одни люди популярнее, другие — нет, одни нужнее, другие — нет, одни талантливее, другие — нет, одни активнее, другие — нет, и так далее.
    
    samsergey Автор
    16.10.2018 07:43
    #19239953
    Совершенно верно! Об этом была вторая из опубликованных глав о "нормальности ненормальности".
    
    Mike_soft
    16.10.2018 07:48
    #19239957
    они не «ужасно-отвратительные», они биологические. самец должен оставить больше своего потомства, поэтому ему нужно оттрахать больше самок, для этого других самцов нужно обходить любыми средствами. и привлекать самок тоже надо. самкам тоже приходится конкурировать за самцов с другими самками… Вот отсюда и растут ноги у большинства стремлений. (а уж как самец обойдет — обгонит, оттеснит, обхитрит — вторично. у каждого свои преимущества и недостатки — один сильнее, другой быстрее, третий умнее, четвертый — хитрее...)
    
    Fracta1L
    16.10.2018 09:03
    #19240113
    они не «ужасно-отвратительные», они биологические
    
    А что насчёт активности химических веществ? Энергии/массы различных объектов? Почему, наконец, Вселенная расширяется, а не спокойно себе пребывает в одном состоянии, почёму одни звёзды светят тускло, а другие ярко, потом взрываются, рассеивая себя в окружающую пустоту?
    
    По-моему, это намного более глубокие законы, чем «самец хочет впендюрить», а биология — только частное проявление этих законов.
    
    Mike_soft
    16.10.2018 09:39
    #19240227
    естественно, биология — частный случай «более глубоких законов» вероятности. а человек — «частный случай биологии».
    
    Taliesien
    16.10.2018 10:19
    #19240395
    Уходя на более глубокие уровни абстрактности всегда легко потерять изначальный смысл. Равно как если проводить аналогии. Любое даже максимально близкое сравнение искореживает смысл. А так то «самец хочет впендюрить» и есть двигатель человечества. Наряду с прочими, как например внутривидовая агрессия. Всю пирамиду Маслоу можно объяснить через примитивные инстинкты.
    И суть в том что социальное равенство невозможно априори. Мы всегда будем стремиться выделиться из стада, оставаясь в рамках стада. Всегда будем ненавидеть стадо, боясь при этом быть изгнанным из него. Именно это заставляет нас шевелиться а не стагнировать в условной зоне комфорта.
    
    Mike_soft
    16.10.2018 10:37
    #19240509
    и вместе с этим будем бороться со «стадами чужаков», объединившись со «своим стадом». а завтра объединимся с ближайшими чужаками, чтоб совместно гнобить «дальних чужаков». а граница между «чужими» и «своими» всегда подвижная. точнее, таких границ много — цвет кожи, религия, паспорт, любовь к футбольной команде…
    
    Fracta1L
    16.10.2018 11:10
    #19240729
    +1
    А так то «самец хочет впендюрить» и есть двигатель человечества.
    
    Это вульгарный фрейдизм (если фрейдизм вообще возможно вульгаризовать). Мотивация несколько сложнее. Тут и потребность в кормлении ЧСВ, и желание много и вкусно есть, и быть свободным от унылой постоянной работы, и многое другое.
    
    riky
    16.10.2018 14:24
    #19242017
    Люди стремятся не к равенству, а к справедливости. Взять все и поделить поровну хотят лишь тунеядцы которые ничего не хотят делать, а получать хотят как у всех.
    
    То есть если человек работает в 2 раза больше то и получать хочется справедливо в 2 раза больше. А в реальности человек работает на заводе день и ночь получает 10тыс, а какой нибудь чиновник 10 млрд. И получается что чиновник работает в миллион раз больше чтоли? Конечно от такого руки опускаются и делать уже ничего не хочется. Это и апатия к жизни и не хочется развиваться.
    
    Fracta1L
    16.10.2018 14:39
    #19242099
    Работать рабочим на заводе может любой кретин. Управлять тем же заводом — уже нет. У чиновников нет зарплат в 10 млрд, и их нелегальное обогащение — отдельная тема.
1. androidt1c
  15.10.2018 10:12
  #19236131
  Как минимум, один важный вывод из статьи есть. Государство должно стремиться не допустить такого состояния: «в моделях, в которых богатые начинают платить преимущественно богатым, а бедные — бедным, общество разваливается окончательно». У нас пока это разделение миров только усугубляется.

vassabi
14.10.2018 19:42
#19234671
+1
также посмотрим на анимированные гифки, которых, увы, в книжке напечатать не получится.
в книге можно сделать как в моем любимом томике Сэджвика про алгоритмы: напечатать серию из 4-х или 6-8-ми рисунков, при разных n (например так было проиллюстрировано различия алгоритмов сортировки ).
1. Sirion
  14.10.2018 23:25
  #19235263
  Можно сделать как-то так)
  
  GIF
  
  samsergey Автор
  14.10.2018 23:49
  #19235287
  Придется многотомник выпускать :)
  
  Vantela
  15.10.2018 10:34
  #19236265
  Ради такого решения демонстрации гиф в книге — можно и многотомник.:)
  
  Хотя ссылки на скажем поясняющий фильм было бы достаточно.
1. samsergey Автор
  14.10.2018 23:49
  #19235285
  Да, именно так я и планирую поступить. Но грех не воспользоваться тем, что в сетевом ресурсе можно показывать мультики!

NickFornit
15.10.2018 00:27
#19235339
А как (не)физик, автор может пояснить, чем отличается термодинамика от произвольности принятия решений, где нет термодинамической статистики, а основой является отклонения параметров гомеостаза от нормы (плохо) и возврат их в норму (хорошо)? Ведь от этого зависит правомерность использования термодинамической статистики в экономике, управляемой осознанной произвольностью.
1. samsergey Автор
  15.10.2018 00:39
  #19235357
  Не уверен, что верно понял вопрос. Замечу что "осознанная произвольность" — это то, что отличает живые системы от неживых, но она не нарушает законов физики. В открытых диссипативных системах возможна самоорганизация, локально понижающая энтропию, но для всей системы, в контексте окружающей среды, деятельность таких необычных флуктуаций энтропию все равно повышают. Экономика управляется осознанно на микроуровне, ансамбль миркоэкономик требует нового управления в виде макроэкономической политики целой страны, ансамбль экономик целых стран тоже хорошо бы регулировать, но тут начнётся борьба с масонами и гегемонией и, полагаю, всё опять вернётся к стохастике. Не любят люди чужого управления, пусть даже и разумного.

ntkj666
15.10.2018 05:53
#19235595
Очитка по Фрейду — "Станем повторять процедуру ОБМАНА снова и снова..."

ganqqwerty
15.10.2018 09:56
#19236059
Ну то есть, если в обществе есть какое-то понимание справедливости (будь то примитивное, равномерное или более тонкое, зависящее от квалификации, риска, полезности, верхнего ограничителя индекса Джини или еще чего-то), то ее установление будет неизбежно искусственным. В противном случае мы предоставляем обществу быть управляемым эволюцией и термодинамикой, и доля процента населения будет владеть близкой к 100% долей благ.

ganqqwerty
15.10.2018 10:06
#19236095
Очень интересно посмотреть моделирование для различных моделей справедливости:
1. Что если мы искусственно будем ограничивать ту или иную метрику, например, не давать коэффициенту Джини подняться выше 0.2 или разнице между наиболее бедными 2% и наиболее богатыми 2% подняться выше чем в 5 раз?
2. Можно ли придумать как моделировать справедливую оплату, где количество получаемых денег зависит от сочетания степени риска, полезности, квалифицированности? Ну типа рискуешь жизнью и идешь в пожарники или шахтеры — молодец, вот тебе наивысшая оплата. Рискуешь капиталом и организовываешь фейсбук — молодец, ты не такой смелый как шахтеры, но получать будешь почти так же много. Затратил кучу усилий для того, чтобы стать космонавтом, да еще и рискуешь жизнью в космосе — будешь даже больше пожарника получать.
3. Различные прогрессивные шкалы — сколько нужно ввести ступеней для каких распределений?
4. Может быть, не прогрессивный налог, а ограничение сверху на зарабатываемую сумму (cap) может интересно сработать?
1. nidheg666
  15.10.2018 16:36
  #19238021
  3. про прогрессивную шкалу рекомендую ознакомиться с «кривой лаффера»
  4. введение потолка будет ограничивать развитие некоторых сфер, ибо для наиболее активных участников рынка и производства пропадёт мотивация. плюс пропадёт возможность вкладывания сверхприбылей в производства.

ganqqwerty
15.10.2018 10:17
#19236157
И еще вопрос: учитывается ли в модели появление новых людей, как-то связанных со старыми? Статистически беднота плодит бедноту, а богатые рождают детишек, которые по тем или иным причинам тоже будут богатыми. С пуассоновскими выбросами в виде миллионеров из трущоб и промотавших состояние люмпенов из высших сословий. Можно ли попробовать вбрасывать новых людей в модель и смотреть, ускорится ли расслоение (интуитивно — вроде да)
1. vassabi
  15.10.2018 11:37
  #19236617
  Можно ли попробовать вбрасывать новых людей в модель и смотреть
  ну, массовое выкидывание «верхней части» (ака революции) в прошлом веке происходило неоднократно, а с выкидыванием «нижней части» (ака базовый доход и проч) экспериментируют в этом веке.
1. samsergey Автор
  15.10.2018 13:58
  #19237167
  Я специально указал использованные алгоритмы, хоть они и предельно просты. Можно усложнять модель, можно вводить новые параметры и играть с этим. Это несложно, увлекательно, но, на мой взгляд, не очень полезно для практического применения. Люди склонны сопротивляться красивым теоретическим решениям или отыскивать в них лазейки.

gatoazul
15.10.2018 11:38
#19236619
Для тех, кто заинтересовался самим подходом:

Классика эконофизики: Farjoun and Machover, «Laws of chaos»
Также интересные модели есть у Cockhsott and Cottrell

Panzerschrek
15.10.2018 12:55
#19236949
Интересная статья, но к реальной экономике она имеет весьма далёкое отношение.
В реальности всё не сводится к безвозмездному обмену деньгами. В реальности есть производство товаров и услуг, обмен, кредит, купля-продажа рабочей силы, выпуск новых денег (через добычу золота, печатание бумажных денег) и ещё куча других экономических явлений.
Если их все учесть, то, возможно, при некоторых обстоятельствах, получится вышеизложенное распределение величины «богатство». Но по факту может так оказаться, что подобное распределение порождается совершенно другими механизмами, отличными от вышеизложенных.
1. samsergey Автор
  15.10.2018 14:13
  #19237229
  +1
  О, я ждал такого комментария! Видите ли, эта серия статей про универсальные свойства распределений случайных величин, про принципы матстатистики и некоторые любопытные закономерности, имеющие математическое объяснение. Она не про экономику, также как законы Мерфи — никакие не законы. А так, вы совершенно правы, реальный мир учитывает всё, что вы перечислили и выдает какие-то распределения, меняющиеся со временем и плохо измеряемые. И народ их аппроксимирует гаммой, Вейбуллом или лог-нормальными распределениями не от безысходности или незнания, а в силу важных аналитических свойств этих распределений, позволяющих дальнейший анализ (устойчивость, бесконечная делимость, максимизация энтропии и т.д.) Вот об этих неочевидных свойствах мне и хочется рассказать.
1. expertykt
  16.10.2018 03:25
  #19239713
  Как показал Капица в работах по народонаселению, «совершенно другие механизмы» не имеют решающего значения для большой стохастической системы. Он также показал, что «куча других экономических явлений» не более чем статистическая погрешность на микромасштабе и никак не определяет глобальный закон. Более того, никакого качественного прогресса человечества нет как класса, а то, что мы видим в микромасштабе как смену парадигмы развития, на самом деле является все тем же самым глобальным законом поведения автомодельного процесса в конкретной точке смены знака первой производной. Как и тысячу лет назад, так и тысячу лет вперед никакие потуги человечества не способны изменить этот закон. И так до тех пор, пока мы останемся животными и будем размножаться. Значение имеет только автомодельность размножения и больше ничего.

expertykt
15.10.2018 12:55
#19236951
В следующей главе хотелось бы увидеть ответ на следующие вопросы:
1) Является ли в действительности богатство стечением обстоятельств и какова доля случайного богатства.
2) Каково будет распределение, если для части людей каждый потраченный рубль увеличивает вероятность получения следующего рубля или уменьшает вероятность потери очередного рубля.
1. samsergey Автор
  15.10.2018 14:21
  #19237267
  На первый вопрос, боюсь, никто вам не ответит. А если ответит, то к нему будет сотня новых вопросов: от чисто методических, до обвинении в ангажированности.
  А на второй вопрос я не берусь ответить, поскольку вводится три новых безразмерных параметра, и численный эксперимент выдаст такое множество разных решений, что одного ответа точно не получится. Поиск аналитического решения мне представляется чересчур громоздким для того, чтобы быть полезным. А вы чего имено ожидаете от этого распределения? Каких свойств?
  1. expertykt
    16.10.2018 03:43
    #19239723
    То ли вы лукавите от страха обвинений в ангажированности, то ли сочувствуете идеям секты гуманистов.
    Не полагаете же вы в самом деле, что множество разных решений могут иметь одинаковую энтропию?
    Я ожидаю увидеть вклад всеобщего образования в благосостояние общества. Предполагаю, его нет. И единственный способ изменить материальное положение заключается в движении. Как вы показали, каждый побывает на каждом месте. Только один успеет, а другой нет. Возможно, процесс можно ускорить до момента достижения желаемого места и затем замедлить, чтобы не вернуться в начало координат.
    
    samsergey Автор
    16.10.2018 04:17
    #19239753
    Ни то ни другое, с моей стороны это развёрнутое и честное "не знаю". А ваши слова о движении, по-моему, и есть ответ.
    
    expertykt
    16.10.2018 04:50
    #19239769
    Было бы интересно показать это математически. Или опровергнуть.
    Все это наверняка давно уже показано более-менее строго. Широко не обсуждается по политическим причинам.
    Надеялся что раз вы в теме, знакомы с такими работами.

fukkit
15.10.2018 13:08
#19236995
Основная проблема математизации гуманитарной науки в том, что большинство простых и красивых математических моделей не имеют ничего общего с реальностью, а сложные и уродливые — слишком специфичны и не подходят для ~~хоть какого-то~~ широкого применения.

Бесконечные упрощения, обобщения, передергивания статьи, смесь низкопробной статистики, теории игр и притянутые за уши физические аналогии, поиск счастья в термодинамике и морально дефектная пресуппозиция о необходимости «понять и принять наш сложный несправедливый мир» оставляют впечатление наваристой каши в голове автора.

Заявления, разумеется, грантоёмкие, мировой капитал одобряет.
1. amarao
  15.10.2018 14:18
  #19237253
  +2
  А зачем вы так обесценили пост?
  1. Упрощения и обобщения люди делают всегда.
  2. Передёргивания? А можно список?
  3. Как можно определить пробу статистики? Какая статистика является высокопробной? Проба статистики говорит о её качестве, или наоборот, о предвзятости? Использование «низкопробная статистика» в комментарии к статье говорит нам что-то о статье или о комментаторе?
  4. Я не увидел «поиска счастья» в статье, зато увидел (простите, мои проекции) желание обесценить в комментарии.
  5. Морально дефектная пресуппозиция подразумевает, что у нас есть где-то мораль, которая должна определять правила математической симуляции? Нет ли в этом элемента субъективности?
  6. И в финале, подкинуть желчи с обвинением автора в корыстном замысле.
  
  Не обесценил — день насмарку.
1. samsergey Автор
  15.10.2018 14:30
  #19237313
  +1
  Не размышляйте о том, что творится в голове авторов, в этом знании нет никакой пользы.
1. nidheg666
  15.10.2018 16:43
  #19238049
  +1
  «Бесконечные упрощения, обобщения, передергивания статьи, смесь низкопробной статистики, теории игр и притянутые за уши аналогии „
  так на этом же построена политэкономия Маркса. и ничего, люди досихпор верят в его версию добавочной стоимости.
  1. fukkit
    15.10.2018 17:29
    #19238257
    Увы, это боль экономической науки, чуть менее чем наполовину состоящей из путанных, противоречивых мыслеизлияний разной степени двинутости философов, пытавшихся выстроить хотя бы минимальную систему понятий и категорий в области гос. управления общественным хозяйством, с другого фронта подпираемой разнокалиберными математиками, фрустрированными отсутствием Нобелевской премии по их первичной специальности и тычущими своим неприкаянным мат.аппаратом в разные части экономического «слона», с умнейшим видом выстраивающими частные технические модели, рассыпающиеся при первых движениях фундамента.
    
    nidheg666
    15.10.2018 17:36
    #19238273
    в данном случае странно выглядит что человек упрекнул данный пост в ангажированности мировым капитализмом… при условии что капитализм (а в особенности капитализм австрийской школы) наоборот топит за отвязку от неработающих моделей и погоней за математическими индексами (по типу ого же ВВП) которые не отражают реального положения дел.
    
    fukkit
    15.10.2018 17:58
    #19238407
    -1
    Меня абсолютно не напрягают безобидные любители поиграться в цифры. У них свой уютный мир, в котором они сами себе многое объяснили и убедились в том на графиках.
    
    Однако, когда после отвлечения внимания дикаря на сверкающие бусы, ему в голову под видом выводов вставляют античеловеческие тезисы:
    
    несправедливость в экономическом пространстве — объективное свойство системы, частью которой мы все являемся
    .
    
    попытки создать абсолютную справедливость по-шариковски всегда проходили с с боем и кровью, а результаты, в силу её неравновесности, существовали недолго.
    
    я нахожу возможным выразить свое к тому негативное отношение.
    
    nidheg666
    15.10.2018 18:06
    #19238451
    +2
    а это уже не экономика. люди все разные и имеют разные способности.
    да, для полноты картины не хватает объективных графиков с распределением IQ, амбиций, итд… но все люди имеют разные набор этих характеристик… а а это тоже влияет на экономическое распределение в обществе.
    
    да, вам может бесконечно не нравится то что в обществе есть неравенство. но с тем же успехом вы можете негодовать от неодинаковости снежинок. а следовательно люди ставящие своей целью равенство задаются абсолютно не тем вопросом.
    
    fukkit
    15.10.2018 20:10
    #19238887
    -2
    Вы либо не отличаете равенство от справедливости, повторяя терминологическую ошибку автора, либо невнимательно читаете текст.
    Не так важно, что нравится лично мне, как то, что является более полезным для общества. Ясное понимание положения вещей (осознанность) и стремление к справедливости, я считаю, являются важными, если не определяющими, условиями развития здорового общества.
    Вещи, в общем-то, азбучные
    
    Fracta1L
    15.10.2018 20:40
    #19238975
    +1
    Справедливость — мутное и противоречивое понятие, так же как и полезность для общества. Просто потому, что разные люди думают по-разному, и то, что для одного справедливо и полезно, для другого — вопиющая дичь и адский вред. Вот это вот и есть азбучная истина.
    
    expertykt
    16.10.2018 04:14
    #19239749
    Проблема в том, что вы оперируете неопределимыми понятиями «равенство», «справедливость», «осознанность», «здоровое общество». Это термины, которые никогда не используют уважающие собеседника люди. Пытаюсь объяснить себе ваши минусы.
    
    fukkit
    16.10.2018 10:05
    #19240327
    -1
    Проблема в навязанном современному обществу и Вам лично релятивизме. Всё в мире относительно, ребята, но не настолько, чтобы прятаться от любых непонятных вам терминов за присказками вида «у каждого своя правда», «объективной истины не существует» и «всё не так однозначно».
    
    Диванные смельчаки против справедливости лишь до той поры, пока не столкнутся с несправедливостью лично. Минимально разумному человеку негоже быть настолько близоруким, чтобы обо всех граблях на свете узнавать исключительно из собственного опыта, а все остальное считать «мутными», «противоречивыми», «неопределимыми» понятиями.
    
    Если внутри вашей головы что-то мутно, противоречиво и неопределено, возможно, лучшим выбором является это прояснить, и (хотя бы для себя) определить, нежели принимать обиженную позу и требовать уважения к своей интеллектуальной лени.
    
    Минусы объяснять не нужно. Люди имеют право высказывать своё мнение — это нормально.
    
    nidheg666
    16.10.2018 11:12
    #19240745
    ок. объясню на пальцах. понятие справедливости крайне неоднозначно. если применять его к вашему любимому коммунизму, то в ранней версии был лозунг:
    
    «от каждого по способностям, каждому по потребностям». справедливо? для людей у которых большие потребности и маленькие способности им это кажется справедливым. но это априори несправедливо для остальных, ибо при вкладывании больших способностей они получают меньше. к чему приведёт мотивационная составляющая данного можете сами додумать.
    
    позже появилась более капиталистическая версия:
    «от каждого по способностям, каждому по труду» — справедливо? вроде как да. но при таком варианте возникает неравенство.
    
    и логичный вопрос вам… а что же тогда в вашем понятии справедливо применимо к данной ситуации?
    
    Fracta1L
    16.10.2018 11:19
    #19240793
    +1
    Всё в мире относительно, ребята, но не настолько, чтобы прятаться от любых непонятных вам терминов за присказками вида «у каждого своя правда», «объективной истины не существует» и «всё не так однозначно».
    
    Обоснуйте.
    
    В пользу релятивизма говорит объективное существование индивидов/слоёв/народов с совершенно разными, подчас противоречащими друг другу системами ценностей.
    
    Диванные смельчаки против справедливости лишь до той поры, пока не столкнутся с несправедливостью лично
    
    Facepalm.
    
    Вам говорят, что справедливость у каждого своя, и потому в качестве общего критерия использоваться не может. Я вижу несправедливым, что с налогов работающих людей выплачиваются немалые суммы мамашам только за то, что они тугосерю запузярили, но мне как-то в голову не приходит требовать «навести справедливость», потому что я в курсе, что для одних деточки это смысл жизни, для других очень важны демографические показатели родной страны, и потому для них эти выплаты совершенно справедливы.

DjSens
15.10.2018 21:08
#19239049
Какая экономическая система будет на космическом корабле, которому 200 лет лететь до места назначения и у которого на борту 1000 человек? А 10000? А 100000?
Я думаю там будет планирование обязанностей и равное распределение благ. Россия от такого корабля отличается только численностью.
Кстати, на хабре за такое минусуют, в итоге социалисты не могут спорить на равных — т.к. "один камент в сутки".
1. mayorovp
  15.10.2018 21:14
  #19239063
  Вот именно в численности и проблема. Чем больше народу — тем хуже работает плановая экономика или коммунизм.
  1. DjSens
    16.10.2018 22:07
    #19243961
    Чем больше народу — тем мощнее нужны суперкмпьютеры чтоб посчитать план. Вассерман тоже так считает.
    Посмотрите в вике чем отличается конкуренция от соревнования и вы тоже не захотите жить в мире конкуренции.
    
    expertykt
    17.10.2018 02:56
    #19244507
    Конкуренция не альтернатива плану, это две принципиально разные системы. При конкуренции каждый руководствуется своей собственной системой ценностей и голосует рублем. Так ресурсы общества распределяются для максимального удовлетворения потребностей. План означает общество, где члены бесправны и только один оракул определяет, что где когда кому и как потреблять. Очевидно, плановые и текущие потребности могут совпасть лишь в среднем, а в каждый конкретный момент времени и места совпадение является случайным. План как сломанные часы показывает правильное время один (два) раза в сутки (плановый период). Да, конкуренция, как и прочие «демократические» механизмы управления, связана с большИми издержками. Но меньшие издержки плана получаются только при упрощении, что человек питается белками, жирами и углеводами, а не пельменями и борщом.
    
    Mike_soft
    17.10.2018 07:31
    #19244643
    +1
    Ну не совсем так. план хорош в плане выживания :-). т.е. когда вам нужно потреблять не «колбасу», а «калории». когда вам нужно не «красивую куртку», а «чтоб не холодно было». не «удобные кроссовки», а «кирзачи тяжелые, зато ноги сухие». т.е. в разрушенной экономике, либо в армии и тюрьме. поэтому даже самые разкапиталистические государства применяли плановые методы в кризисах.
    
    expertykt
    17.10.2018 07:52
    #19244685
    -1
    Применять план в кризис и превращать кризис в план это немного разное, не находите?
    
    Mike_soft
    17.10.2018 08:00
    #19244697
    не совсем понял, что вы хотели сказать…
    но еще раз повторюсь: методы плановой экономики способны обеспечить выживание в критических, стесненных, несвободных обстоятельствах. и сделать это достаточно эффективно и быстро, но грубо.
    т.е. область применения плановой экономики — разрушенная страна, армия и тюрьма. не более
    
    expertykt
    17.10.2018 08:09
    #19244713
    -1
    Хотел сказать, что связь глубже: результат плановой экономики — разрушенная страна, страна — армия и страна — тюрьма.
    
    Mike_soft
    17.10.2018 09:10
    #19244841
    если вовремя не остановиться…
1. Fracta1L
  15.10.2018 22:02
  #19239171
  +1
  в итоге социалисты не могут спорить на равных
  
  Чтобы спорить на равных, нужно вооружиться аргументами вместо низкопробного словоблудия. Сравнить страну с космическим кораблём — ну прям чувствуется блеск интеллекта. Чо б с казармой не сравнить, и не наделать из этого сравнения выводов космического масштаба?
1. expertykt
  16.10.2018 04:00
  #19239737
  Соглашусь полностью с предыдущим комментом. Именно количество населения определяет не только применимый к этому населению закон, но и положение этого общества в конкретной точке на графике этого закона.
  Добавлю, социалистическая идея справедливости аморальна по сути. Поэтому ее нет в Библии. Синонимом социалистической справедливости является тоталитаризм.
1. dTex
  16.10.2018 12:11
  #19241083
  корабль имеет вполне конкретную цель — доставить колонистов в новый мир с минимальными издержками. Все остальные цели и "потребности" в таком случае должны быть подчинены этой одной цели. В условиях ограниченных ресурсов, оптимальным на таком корабле будет не какой-то там социализм, по труду и по потребностям, а анабиоз в той или иной форме. Т.к. с точки зрения цели корабля, любая активность экипажа будет только ухудшать условия достижения этой цели (марксистам читать так — труд экипажа не будет создавать прибавочной стоимости).

maslyaev
15.10.2018 22:26
#19239271
Шикарная статья. Спасибо. Аж у самого руки зачесались погонять модельки.

несправедливость в экономическом пространстве — не следствие поганой человеческой натуры, а объективное свойство системы, частью которой мы все являемся
А вот здесь физикам и техникам (точнее, системотехникам) следует увидеть не проблему, а задачу. Что можно было бы прикрутить к системе такого, чтобы с одной стороны не угробить мотивацию субъектов к экономической деятельности, а с другой — увести систему от стремления к ситуации, показанной на последней гифке?

Мне кажется, имеет смысл подумать о встраивании механизма, мягко подталкивающего систему к тому самому вырожденному состоянию им. тов. Шарикова, энтропия которого равна нулю. Допустим, в цикл модели встраиваем такого жучка: раз в количество итераций, по порядку величин, сопоставимом с n отбираем у всех участников по 1% богатства и делим равномерно на всех. Те игроки, у которых меньше M/n, получают в дебет, а у кого больше — в кредит.

Чем-то это похоже на старое знакомое (и справедливо всеми ненавидимое налогообложение), но на самом деле нет. Налогообложение обдирает всех, но выручку отдаёт самому богатому игроку, который уже дальше в зависимости от настроения или раздаст сокровища голодающим, или промотает на всякие глупости.

Что интересно, описанная схема с процентом вполне реализуемая чисто технократическими мерами (т.е., выражаясь технически, на уровне протокола). Без прибегания к услугам аппарата принуждения.
1. expertykt
  16.10.2018 04:05
  #19239741
  Почему вы считаете, что модель Шарикова лучше? Для кого лучше? Хотите сделать шариковым Преображенского? Полагаю, критерий лучшести должен иметь чисто математическое и ни разу не моральное основание.
  1. maslyaev
    16.10.2018 13:01
    #19241409
    +1
    Математика — просто инструмент. Она не поможет нам разобраться в своих желаниях. Желания мы должны сформулировать сами, а математика поможет выработать оптимальный способ их реализации.
    
    Сильное социальное расслоение — проблема, не доставляющая радости ни тем, кто обитает на дне, ни богатенькой верхушке. Быть самым сказочно неприлично богатым среди голытьбы, убожества и безнадёги прикольно только первые пять минут. А потом даже если напрочь отбита способность к сочувствию, всё равно встаёт проблема безопасности.
    
    Речь вовсе не о том, чтобы отнять и поделить, а о том, что неплохо было бы сделать так, чтобы естественным стационарным состоянием денежной системы стало «всем поровну». «Естественное стационарное состояние» вовсе не обязано быть тем состоянием, в котором система фактически пребывает, а то состояние, в которое всё само собой скатывается при отсутствии целенаправленной активности. Профессор Преображенский — востребованный специалист и работает как проклятый, и естественно, что у него и кабинет, и операционная, и столовая. Если решит совсем уйти от дел, с ништяками, понятное дело, придётся расстаться, но он всё равно не пропадёт, потому что в том самом «естественном стационарном состоянии» ему хватит и на комнатушку, чтобы кости бросить, и на дошик.
    
    В китайский философии есть два интересных понятия — Дао и Дэ. Дао — естественный порядок вещей, а Дэ — наше человеческое шило в заднице. Согласно Лао-цзы, задача мудрого правителя — воспитание Дао. Можно предположить, что Дао правильной денежной системы выглядит как-то так:
    1. Для того, чтобы быть экстремально бедным, нужно вести себя совсем глупо (например, жёстко бухать). Как только перестаёшь откровенно косячить, твоё благосостояние потихоньку поправляется.
    2. Быть экстремально богатым экстремально сложно и невыгодно. То есть теоретически поиметь миллиард баксов можно, но обслуживание владения им стоит запредельно дорого. Как только перестаёшь прикладывать сверхусилия, твоё благосостояние потихоньку поправляется, только уже в минус.
    
    Сейчас же мировая финансовая система устроена таким образом, что бедным легче беднеть, а богатым легче богатеть. То есть имеющееся Дао работает с точностью до наоборот. Если ты бедный, ты должен сверхнапрячь своё Дэ чтобы выбиться в миддл-класс, и только после этого можешь оседлать течение и стать богатым. В правильной фин. системе ты можешь быть очень богатым, но только если умеешь и согласен постоянно прилагать к этому усилия.
    
    Mike_soft
    16.10.2018 13:09
    #19241471
    проблема безопасности решается относительно просто, особенно в условиях олигархии — т.е. сращивания власти с крупным бизнесом.
    примеров в современной России более чем достаточно.
    
    Fracta1L
    16.10.2018 13:18
    #19241513
    Проблема социального расслоения не в том, что самый богатый получает и имеет в 1000 раз больше самого бедного, а в том, как живёт этот самый бедный. Одно дело, когда самый бедный способен обеспечивать свои базовые потребности (платить за жильё, покупать более-менее нормальную еду и одежду, выбираться хотя бы раз в месяц в увеселительные заведения, иметь доступ к информации и образованию), и совсем другое — когда он живёт в теплотрассе и дерётся с бродячими собаками за объедки. В первом случае людям становится почти что безразлично, что у богатеев яхты с виллами.
    
    samsergey Автор
    16.10.2018 13:24
    #19241565
    Спасибо! Вы очень точно выразили то, что я думаю на этот счет.
    
    Fracta1L
    16.10.2018 13:30
    #19241599
    чтобы естественным стационарным состоянием денежной системы стало «всем поровну»
    
    Тут я бы поправил: не «всем поровну», а «всем неплохо»
    
    expertykt
    17.10.2018 03:54
    #19244525
    Вы лукавите с первой строчки, постулируя необходимость исполнения желаний, но не указывая, чьи желания должны исполняться в ущерб чьим. Принимая во внимание, кто кого уплотнял, методом исключения получаем, что желания Преображенского для вас априори не имеют значения.
    Во второй строчке вы заблуждаетесь, постулируя способность человека действовать по своей воле для своего блага и способность общества действовать во благо общества. Практика показывает обратное. Беспристрастный научный анализ объясняет это тем, что законы нашей природы намного сильнее способности человека к «разумному поведению». Разумное поведение вообще миф, это лишь внешнее проявление естественного и неизбежного следствия количества населения, в т.ч. количества контактов индивидуумов, их концентрации и стратификации. В первобытно-общинном обществе было «больше справедливости» не вследствие высоких моральных качеств людей, а вследствие очень низкой их концентрации, вследствие этого низкой специализации и вследствие этого низкого разделения по благосостоянию. Простая математика и никакого гуманизма.
    Дальнейшие бессвязные рассуждения, имеющие только эмоциональную, но не логическую связь с объявленными ложными основаниями, приводят к совершенно парадоксальному выводу о некой «правильной фин.системе» и мифическому барьеру между бедными и богатыми. Как хорошо сказал Капица, это все случайные флуктуации микромасштаба. В то время как базовых характеристик глобального масштаба вы вообще не видите.
    В этом смысле радует политика государства по увеличению продолжительности активной жизни человека и рождаемости, поскольку именно эти параметры лежат в основе экономики человечества на протяжении всей ее истории. Искуственное локальное увеличение этих параметров дает наибольший прирост экономики в сравнении с любыми другими усилиями. Отсюда и пенсионная реформа, и материнский капитал, и национальные программы по медицине и образованию, бессмысленные с точки зрения текущего бюджета.
    
    maslyaev
    17.10.2018 11:53
    #19245521
    Зачем желания должны исполняться обязательно кому-то в ущерб? Экономика — игра с ненулевой суммой, и ущерб возникает тогда, когда или кому-то удаётся стянуть на себя со всех одеяла, или когда кадавры финансово неудовлетворённые мучаются своими звездостраданиями в духе «хотел на первую строчку Форбс, а скатился с 30-й на 40-ю...».
    
    Во второй строчке вы заблуждаетесь, постулируя способность человека действовать по своей воле для своего блага и способность общества действовать во благо общества.
    Во-первых, извините, не нашёл того место, где я это постулирую. Во-вторых, что не так с этим постулатом? Кто, если не мы, у нас способен действовать по своей воле для своего блага? Только цари, боги и герои?
    
    Разумное поведение вообще миф
    Понимаю. Согласно всесильному «потому что верному» учению Маркса-Энгельса-Ленина-Сталина-Мао не существует никакого разумного поведения, а также чести, совести, правды и любви. Есть только атомы, пустота, законы исторического развития и рррреволюционная целесообразность. Поэтому, говорят, если во благо законов развития революционно-целесообразно закопать по канавам десяток-другой миллионов людишек, то и нет проблем. В конце концов, выстрелами в затылок всё равно невозможно уничтожить ни атомы, ни пустоту. Так?
1. Fracta1L
  16.10.2018 12:20
  #19241143
  Можно придумать такую систему, по которой капитал в виде личного имущества, денег, предметов роскоши будет облагаться повышенными налогами, а капитал в виде инвестиций в производство, ФОТ, и прочие подобные вещи — нет. Но я чот подозреваю, что лазейки всё равно найдут + это лишний коррупционный фактор. Вообще, прежде чем запускать руки в карманы богатых, нужно сначала свести коррупцию до цивилизованного уровня, а для этого нужны нормально работающие демократические институты.
  1. maslyaev
    16.10.2018 14:33
    #19242057
    Налогообложение в том виде, в котором мы его знаем, как я сказал выше, на редкость кривой вариант. Неэффективный и, Вы правы, неизбежно порождающий коррупцию.
    
    Не надо запускать руки ни в чьи карманы. Пусть богатые сами запускают руки в свои карманы. Когда им самим это зачем-нибудь бывает нужно. То, о чём я говорю — это «налог» (в кавычках, потому что это не налог в том смысле, к которому мы привыкли) на владение деньгами. Именно владение, а не операции. Именно деньгами, потому что все остальные активы (движимое и недвижимое имущество, владение долями в капитале, дебиторская задолженность, золото в слитках и т.п.) в расчёт не берём. Только деньги.
    
    По сути, «налог» на владение деньгами уже есть. Называется инфляцией. Но только он неправильно устроен. Во-первых, эмиссионный доход уходит самому богатенькому (государству), а во-вторых, обесценивание денег стимулирует ростовщичество (т.е. опять же, богатые богатеют, а бедные беднеют). Известна схема, свободная от этих недостатков. В этой схеме и ценность денежной единицы стабильна (это капец как удобно всем), и нет привилегированного игрока (минус коррупция), и технократичная реализация, что называется «на уровне протокола», воспринимаемая всеми игроками как понятные и предсказуемые правила игры. Кроме того, становится осмысленной потому что выгодной операция давания денег под нулевой или даже отрицательный процент.
    
    Fracta1L
    16.10.2018 15:04
    #19242273
    +1
    Что за схема?
    
    maslyaev
    16.10.2018 16:21
    #19242645
    Так называемые «свободные деньги» Сильвио Гезелля. Тема, над которой, насколько мне известно, даже не принято думать. Не смотря на то, что опытные эксплуатации пройдены феноменально успешно.
    
    Сейчас, когда народ привык к электронным деньгам, даже не нужно всё это напряжное рукоделие с наклеиванием марочек. Плюс к тому, можно организовать не только отъём «налога», но и раздачу отнятого по принципу им. тов. Шарикова, то есть всем поровну.
    
    Fracta1L
    16.10.2018 16:37
    #19242739
    Погодите, я чот не понял. Если эти деньги автоматически теряют в цене со временем, то каким образом
    
    ценность денежной единицы стабильна
    
    если это та же инфляция, только в профиль? И каким образом будет выгодна
    
    операция давания денег под нулевой или даже отрицательный процент
    
    если в сочетании с демереджем это дико невыгодно?
    
    Пока что я вижу всё достоинство этой схемы в том, что прибыль от обесценивания денег не достаётся банкам, а исчезает в никуда, но это и достоинством-то трудно назвать.
    
    maslyaev
    16.10.2018 17:35
    #19242995
    Допустим, у нас есть мешок со ста рублями.
    Со стандартной инфляцией через месяц в мешке по-прежнему 100 рублей, но купить на них уже можно столько месяц назад можно было купить на 99 рублей.
    Рублики обесценились на 1%.
    
    С новой прекрасной инфляцией смотрим через месяц в мешок, а там не 100 рублей, а всего 99. Покупательная способность рублика такая же, как месяц раньше (ценники перерисовывать не надо). Изменилась покупательная способность мешка.
    Мешок обесценился на 1%. А рубль не обесценился. То, что месяц назад можно было купить за рубль, то же самое и сегодня продаётся за рубль.
    
    Когда мы имеем пагубную привычку хранить сбережения в деньгах, разницы никакой. 1% отстёгиваем и так, и так. Но у денег есть не только функция накопления богатств, но и ещё две другие функции:
    1. Единица измерения стоимости. Что бы Вы сказали, если бы метр менял свою длину в зависимости от обстоятельств, или продолжительность секунды была бы плавающей? Нестабильность единицы измерения — это какая-то метрология курильщика. Нам очень не повредила бы метрология здорового человека.
    2. Расчётная функция. Если я два раза в месяц получаю зарплату и всю её трачу, то мои потери в среднем получаются 0.25%. Вообще не о чем говорить. Если я коммерсант, тратящий выручку на закупку следующей партии товара на следующий же день, то мои потери 0.03%. Тридцать копеек с тысячи рублей.
    
    Про выгодность давать под отрицательный процент. Допустим, у меня нарисовался миллион. Например, что-то продал. Я знаю, что если ничего не предприниму, через месяц в моей кубышке будет на 10 т.р. меньше. Меня душит жаба. Я одалживаю товарищу этот миллион под минус 0.2% месячных, и тем самым экономлю 8 т.р. Нравится. А если товарищ согласится взять под 0%, я его, благодетеля, расцелую.
    
    Fracta1L
    16.10.2018 18:07
    #19243151
    Звучит как минимум интересно.
    
    maslyaev
    16.10.2018 18:43
    #19243307
    Типа того. Чтобы было ещё интереснее, расскажу про ещё одну фичу. Денежная масса — такая штука, которую полезно уметь регулировать. Без механизма регулирования метрологию здорового человека поиметь невозможно. Если ден. массы недостаточно, цена монетки растёт, а если избыток массы, то падает. И то, и другое — зло. Для сдерживания роста нужен механизм эмиссии, а для сдерживания падения — механизм изъятия. В Гезеллевских деньгах изъятие (а это, между прочим, самый тусклый пункт) уже заложено в саму основу. Если дополнить схему шариковскими раздачами всем поровну, то имеем механизм эмиссии. Изъятие у нас константа (тот самый, например, 1% в месяц), и рулёжка идёт эмиссией.
    
    В нормальной ситуации (биржевой курс внутри требуемого коридора) шариковская эмиссия по общей сумме копейка в копейку совпадает с суммой изъятия. Если денежка обесценилась, стопорим эмиссию, ден. масса уменьшается и, как следствие, курс возвращается на место. Если денежка выползла за границу коридора в плюс, эмитируем вдвое больше обычного, и курс возвращается на место. Динамическое регулирование. Ничего необычного.
    
    Mike_soft
    17.10.2018 12:11
    #19245621
    вместо внедрения описанной вами системы проще сразу выпустить указ о введении коммунизма. издержек меньше, вау-эффект хороший, а реализация все равно невозможна…
    
    maslyaev
    17.10.2018 12:33
    #19245741
    При чём здесь коммунизм, когда это в чистом виде анархо-капиталистическая тема? ;)
    
    Насчёт невозможности. Один умный дядька сказал, что возможно всё, существование чего не противоречит самому себе. Описанная здесь схема сама себе не противоречит, поэтому есть все основания априорно считать её возможной. Тем более, что это, напомню, неоднократно доказано на практике.
    
    expertykt
    17.10.2018 04:12
    #19244529
    Интересно в плане психической патологии?
    
    Описанная система предполагает неизменность структуры и объема потребления. В противном случае одни товары станут в избытке, другие в недостатке и вот оно изменение покупательной способности рубля aka инфляция.
    Это полный абсурд настолько, что это невозможно без использования магии. Неважно какая погода — топим как в прошлом году, неважно какой урожай — собрать нужно ровно столько как в прошлом году, неважно что все не вечно — в прошлом на ремонт не тратили и сейчас нельзя и т.д. и т.п.
    
    Fracta1L
    17.10.2018 07:56
    #19244691
    Там ещё проблема и с тем, что цены постоянны, а ведь ценовая динамика — важный канал информации для производителей и потребителей.
    
    expertykt
    17.10.2018 08:07
    #19244709
    Да вообще море проблем с постоянными ценами. Фактически паралич экономики и деградация общества. И в результате нищий народ-победитель и процветающий побежденный в кратчайший срок.
    
    maslyaev
    17.10.2018 12:38
    #19245783
    Зачем постоянные цены? Из того, что ценность денежной единицы стабильна, вовсе не следует, что никто никогда не перерисовывает ценники. Только если сейчас их приходится перерисовывать в том числе из-за нестабильности единицы измерения, то в рассматриваемой схеме у нас этот фактор уходит. А изменение рыночной конъюнктуры и всё, что нам рассказывали про спрос и предложение — остаётся на месте и никуда не девается.
    
    mayorovp
    16.10.2018 22:43
    #19244035
    Все это чудесно, но есть проблема. Инфляция как явление никуда не пропадает. Ее все еще нужно измерять чтобы установить правильную ставку налога. Если допустить ошибку — то у нас будет одновременно меняться и количество денег в мешке, и стоимость этих денег. Вместо упрощения все усложняется.
    
    maslyaev
    16.10.2018 23:42
    #19244177
    Да, не пропадает. И в отношении мешка с деньгами, лежащем на расчётном счету ведёт себя ровно так же, как и обычная. Но на этом сходства заканчиваются.
    
    Ключевое отличие в том, что прекрасная новая инфляция с абсолютной точностью известна на много лет вперёд. То есть процент инфляции можно высечь в камне и разместить на фронтоне центробанка. Суммы шариковских раздач заранее неизвестны, поскольку это руль, которым подруливается денежная масса в зависимости от экономической ситуации (а ситуации разные бывают), но инфляция — скала. Сказали, что будет 10% годовых (чуть меньше того 1%/мес., который взят для иллюстрации принципа), так и будет, лишь едва заметно подрагивая в високосные годы. Определённость — это, конечно, не так весело, но зато удобно.
    Неопределённость порождает то, что банкам приходится перестраховываться, закладывая ссудный процент выше возможной инфляции. Высокий ссудный процент больно бьёт по потребителям кредитов. Иногда бьёт насмерть, что для банков прямой убыток. В общем, от описанной схемы выигрывают все. Да-да, так бывает. Денежная система только кажется игрой с нулевой суммой, но на самом деле она есть часть экономики, которая совсем не есть игра с нулевой суммой.
    
    Кроме того, давайте посмотрим, как центробанки управляют инфляцией. Для управления у центробанка есть два инструмента — эмиссия и изъятие. Если инфляция меньше целевого значения (или вообще наблюдается дефляция, что для экономики вообще беда), применяют эмиссию. Эмиссия — всегда легко и приятно. Допечатали триллион — по сути вынули его из ниоткуда и положили в карман. Красота. А вот с изъятием ден. массы совсем другая история. Нужно заработать триллион (например, продать добытое кровью и потом золото или валюту) и спалить этот триллион в печке. Как правило, в таком случае серьёзно душит жаба. Да и золота с валютой, бывает, нет в наличии.
    
    Представьте себе автомобиль, в котором руль работает только в одну сторону. Например, вправо. А влево — с большим трудом, и то если только иногда и чуть-чуть. Экономическая ситуация — как извилистая дорога, на которой одинаково легко нужно уметь рулить в обе стороны. Гезеллевские деньги дают эту гибкость. Может быть, Вы знаете какую-нибудь другую схему, позволяющую рулить в обе стороны ден. массой? (неуёмное наращивание госдолга, пожалуйста, не предлагайте)
    
    mayorovp
    17.10.2018 07:42
    #19244663
    А что вы будете делать когда эмиссия уже нулевая, а инфляция все лезет?
    
    maslyaev
    17.10.2018 11:18
    #19245369
    Ну да, рулёжка в минус ограничена заранее заданным процентом «налога». То есть если случился ацкий катаклизм и денежную массу надо по хорошему сбросить вдвое, то при 10% годовых раньше, чем через 6 лет мы штатными методами этого не добьёмся. Но ведь добьёмся же! 6 лет — это среднесрочная перспектива.
    
    Здесь возникает интересный психологический эффект, который гасит биржевую панику. Когда вниз уходит обычная валюта (или акции, или что угодно), сразу возникает вопрос: это навсегда или только временно? Вот Биткоин, например, просел до 6000 — это всё, обратно к 15-20 тыс. он никогда не вернётся, или всё же вернётся? Или рубль. Будет он когда-нибудь стоить 50руб/$? Может быть да, а может быть и нет. А Гезеллевская ден. единица даже если из-за неудачно сложившейся экономической обстановки и просаживается, всё равно есть уверенность, что в некоторой если не кратко-, то точно в среднесрочной перспективе она обязательно вернётся к целевым значениям.
    Гезеллевская монетка — вообще самый скучный в мире актив с точки зрения валютно-биржевой игры. Все знают, что никакого фантастического роста и никаких катастрофических падений не будет. Только вялое бултыхание внутри заданного узкого коридорчика.
    
    mayorovp
    17.10.2018 12:24
    #19245683
    А почему вы так уверены, что когда-нибудь она обязательно вернется в норму?
    
    maslyaev
    17.10.2018 13:23
    #19246053
    Не понимаю, в чём здесь может быть принципиальный затык. О деньгах ведь вполне можно говорить как о ресурсе, подчиняющемся старым знакомым законам спроса и предложения. Если избыток, то цена меньше, если недостаток — больше. Подруливая существующим объёмом, мы выводим цену на целевое значение. Разве нет? Что может помешать кроме того, что в очередной раз на каком-нибудь куске суши очередной безумец возьмётся отменять законы спроса и предложения?

andrey465
16.10.2018 17:23
#19242943
В статье помимо прочих рассмотрен вариант «Если расходы при обмене пропорциональны достатку» а также упомянут вариант если обмен будет происходить между группами а не индивидуумами.
А аналоги таких систем существуют в реальности (хотя бы в нише) или чисто теория?

Теория счастья. Термодинамика классового неравенства +40

Подходите, всем хватит!

Новая экономическая политика!

Люди — молекулы

Дао выраженное словами — не истинное Дао

Экономика должна быть экономной

Комментарии (106)

samsergey Автор

samsergey Автор

samsergey Автор

samsergey Автор

samsergey Автор

samsergey Автор

samsergey Автор

samsergey Автор

samsergey Автор

samsergey Автор

samsergey Автор