Что общего между снежинкой, капустой Романеско, морской звездой, молниями и деревьями? Так сразу и не скажешь, но с математической точки зрения у всех этих объектов есть общая черта — фрактальность. В глазах математика все в нашем мире подчиняется законам «царицы наук». Любое явление, процесс или объект можно выразить в математической форме, что позволяет его проанализировать под новым углом, так сказать. Многие годы ученые пытаются создать идеальную математическую репрезентацию генов, их взаимосвязи и процессов, в которых они участвуют. Сегодня мы поговорим о том, как фракталы помогли заложить фундамент совершенно новой математической модели генов человека с позиции онкологических заболеваний. Что такое фрактал, чем он так важен для генетиков и математиков, и как новая математическая модель может помочь современной медицине? Ответы будем искать в докладе исследовательской группы. Поехали.

Теоретическое отступление

Для начала стоит вкратце разобраться, что есть фрактал и с чем его едят.

Фрактал — это множество со свойствами самоподобия. Проще говоря, когда что-то состоит из нескольких мини-копий самого себя.



Фракталы встречаются в различных физических явлениях: от диффузии до турбулентности. Это можно назвать естественными проявлениями фракталов. Люди также нашли фракталам применение: в компьютерной графике, радиотехнике, сетевых технологиях и т.д.

Очень красочно фракталы представлены в фильме «Доктор Стрэндж» (2016 г.), когда Старейшина отправляет главного героя на экскурсию по параллельным измерениям.


Немного неприятное зрелище, но наглядно демонстрирующее фрактальность.

Даже на полках супермаркета можно встретить проявления фрактальности, а именно на примере капусты Романеско или цветной капусты.

Если же учесть, что типов множеств с фрактальными свойствами довольно много, можно утверждать, что практически все вокруг нас тем или иным образом связано с фракталами. И организм человека, в особенности его гены, не исключение. Поскольку фракталы можно математически пояснить, разложив по полочкам составляющие, применение подобной модели на генах человека может значительно помочь в понимании различных процессов, протекающих у нас в организме, в том числе и разных заболеваний, патологий и других неприятных вещей.

Одним из важнейших процессов в нашем теле является экспрессия генов (изображение 1а), когда наследственная информация генов преобразуется в функциональный продукт. Другими словами, наши клетки посредством экспрессии генов контролируют свою структуру и функции. Наши гены это база данных, из которой черпают информацию все клетки тела, выполняя необходимые функции в последствии. Потому у нас и не растут волосы во рту, иммунитет борется с инфекциями, клетки крови транспортируют кислород и т.д. Все эти процессы протекают именно за счет программирования клеток на выполнение конкретных задач, что в свою очередь возможно посредством синтеза белка от активации определенного гена.


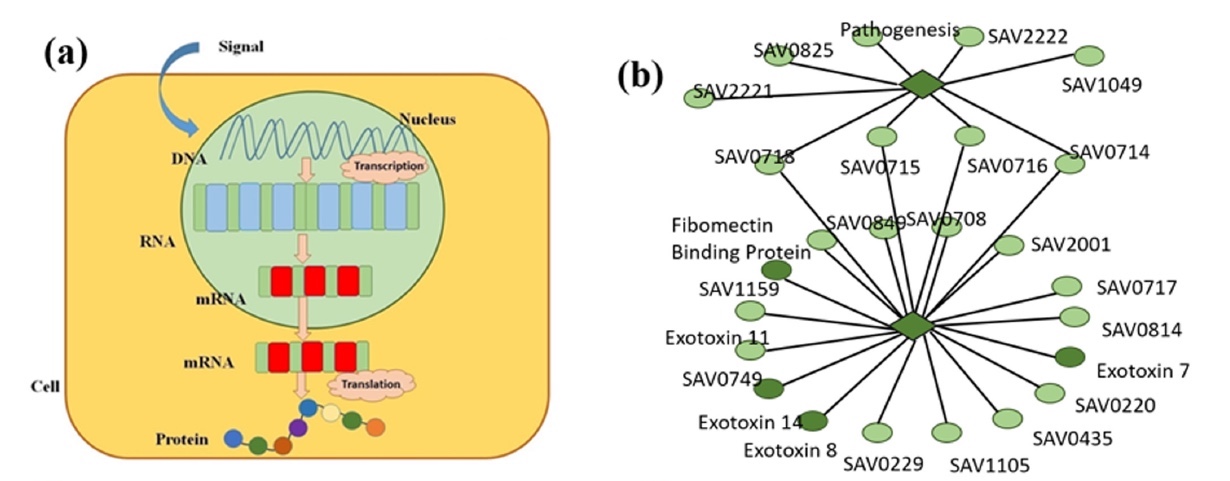
Изображение №1

Регуляция экспрессии генов указывает когда, сколько и как долго должны продуцироваться определенные белки. Посему исследование этого процесса имеет огромную важность для полного понимания того, как работают те или иные механизмы управления организмами.

Этот сложный процесс важен для ученых, поскольку получив возможность им управлять, они смогут создать определенные синтетические клетки, наделенные четкими функциями, в частности, доставка лекарства от онкологических заболеваний в самое «сердце» недуга для более эффективного лечения.

Дабы усовершенствовать методики лечения таких заболеваний, необходимо более детально узнать генетический аспект. Для этого ученые предлагают представить организм человека в виде программы, где гены выступают в роли строк кода, которые можно изменить, если программа работает со сбоем. Чтобы это реализовать, необходимо для начала создать математическую модель гена. На данный момент такие модели уже существуют, но они не могут быть репрезентативными ввиду того, что нацелены были на исследование динамики в сети генов. В данном же исследовании, применившем понятие фракталов, ученые решили сконцентрировать свое внимание на процессе экспрессии конкретного гена, а потом применить взаимную корреляцию между парами ген-ФТ* (1b).

Фактор транскрипции (ФТ)* — белок контроля синтеза мРНК, содержащую информацию о первичной структуре белков, на матрице ДНК посредством связи с определенными участками ДНК.

Проще говоря, ученые решили копнуть поглубже, рассмотрев не всю «стену» целиком, а отдельные «кирпичики».

Результаты исследования

В роли испытуемых в данном исследовании выступили грибок Saccharomyces cerevisiae (пекарские дрожжи) и бактерия Escherichia coli (кишечная палочка).

Посредством анализа статистических данных генетической экспрессии подопытных был вычислен коэффициент Хёрста*.

Коэффициент Хёрста* — мера анализа временного ряда.

Временной ряд* — совокупность статистических данных, собранных в разные временные промежутки, о каком-либо показателе.

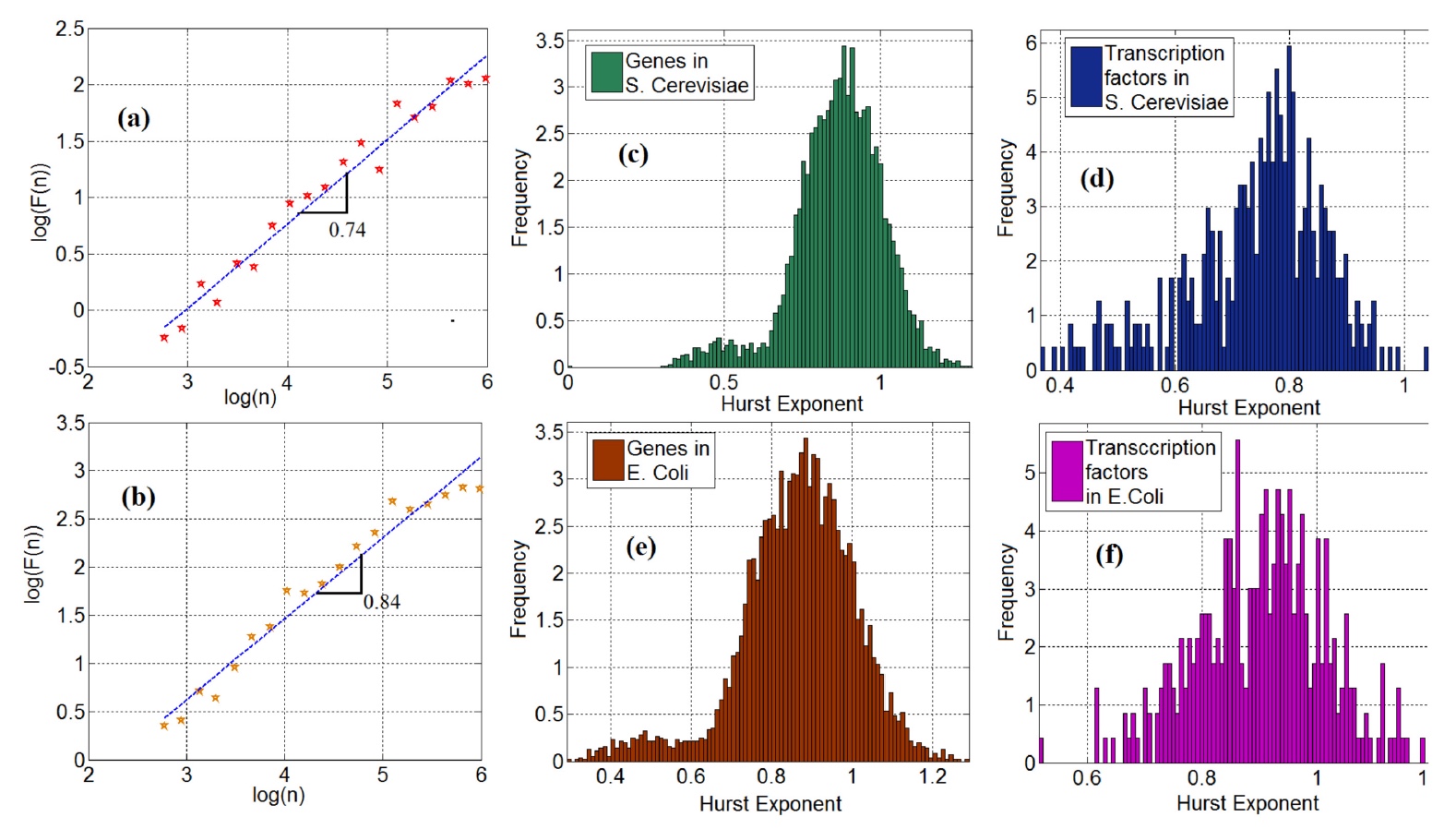
Изображение №2

На изображениях 2а (дрожжи) и 2b (кишечная палочка) показаны билогарифмические графики* флуктуации, как функции масштаба временных рядов ФТ.

Билогарифмический график* — двумерный график данных, использующий логарифмическую шкалу на обеих осях (вертикальной и горизонтальной).

Наклон кривой на этих графиках соответствует коэффициенту Хёрста. Стоит отметить, что 95% (дрожжи) и 98% (палочка) временных рядов генов продемонстрировали долгосрочную зависимость*.

Долгосрочная зависимость* — показатель в анализе временных рядов, обозначающий медленное затухание статистической зависимости двух точек с увеличением временного интервала между ними. Определяется показателем коэффициента Хёрста — от 0 до 1. Если показатель выше 0.5, то мы имеем сильную долгосрочную зависимость, ниже 0.5 — противоположный эффект.

Коэффициент Хёрста долгосрочной зависимости в данном конкретном случае составил 0.5, что говорит об ее отсутствии, в теории. Однако дальнейший анализ данных показал, что этот показатель превышает значение в 0.5, что говорит о наличии долгосрочной зависимости временных рядов в генетической экспрессии (2с и 2е). Это наталкивает на то, что временные ряды ген-ФТ не могут рассматриваться как нечто случайное, потому должны моделироваться на базе марковской цепи, когда существует череда событий, случайность каждого из которых зависит исключительно от предыдущего события.

Подобно генам, факторы транскрипции также показали долгосрочную зависимость: в 97% для дрожжей и для палочки (графики 2d и 2f).

А теперь добавим щепотку фрактального анализа в общую чашу. Для начала ученые обращают наше внимание на бимодальность распределения коэффициента Хёрста. Лучше всего это видно на графиках 2с и 2е. Ученые объясняют это наблюдение тем, что в экспрессии генов имеются и диффузионные процессы, обладающие несколькими диффузионными потенциалами. Посему бимодальность можно пояснить неравновесным броуновским движением с разными потенциалами. Но это утверждение требует дополнительных доказательств, поисками которых ученые займутся в следующих исследованиях.

А сейчас мы вернемся к мультифрактальности. Ученые применили мультифрактальный анализ детрендовых флуктуаций для определения наличия/отсутствия мультифрактальных характеристик у временных рядов экспрессии гена. Этот анализ показал наличие таковых как у генов, так и у ФТ.

Также ученые применили методику бутстрэп* для точного определения (точнее для подтверждения) наличия долгосрочной зависимости, учитывая ограниченность длин экспериментальных временных рядов.

Бутстрэп* — методика анализа статистики вероятностных распределений.

Для каждого временного ряда экспрессии гена было подготовлено 10 случайных под-интервалов, каждый из которых содержал 90% упорядоченного фрагмента исходного временного ряда. Далее для всех вариантов был рассчитан коэффициент Хёрста. Таким образом была получена разница между показателями экспериментального временного ряда и случайных версий. Для кишечной палочки разница составила всего 0.006%, а для пекарских дрожжей и того меньше — 0.0001%. Таким образом было подтверждено наличие долгосрочной зависимости в обоих образцах.

После рассмотрения интересующих характеристик гена и ФТ по отдельности, ученые приступили к анализу пар ген-ФТ, как единого объекта. Вычисление показателя взаимной корреляции показало, что 98% пар ген-ФТ (в обоих образцах) обладают свойствами долгосрочной зависимости (3а).


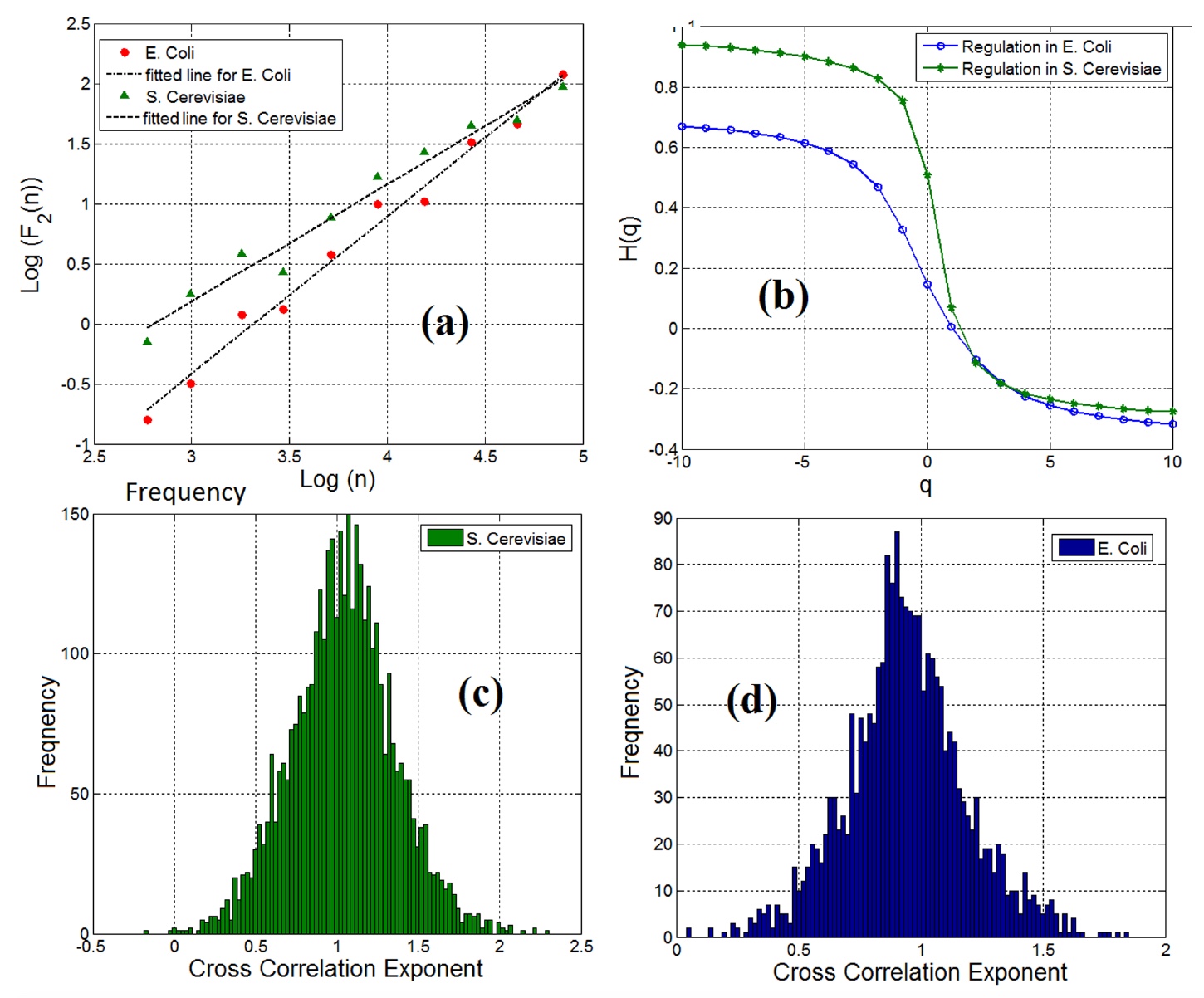
Изображение №3

Мультифрактальный анализ детрендовых флуктуаций подтвердил наличие мультифрактальных особенностей в парах ген-ФТ (график 3b).

Стоит отметить — независимо от того, что наблюдались и фрактальная, и долгосрочная взаимная корреляция в парах генов и факторов транскрипции в сетях регуляции генов, взаимная корреляция не была одинакова для всех пар. На графиках 3с (дрожжи) и 3d (кишечная палочка) отображен показатель взаимной корреляции пар ген-ФТ.

Ученые использовали эти графики для измерения информационной энтропии и, как следствие, информационного содержания сети регуляции генов по различным типам клеток для количественного анализа и спецификации сетей регуляции генов.Показатели энтропии составили: 4.18 — дрожжи, 5.29 — кишечная палочка. А это говорит о том, что сеть экспрессии генов у пекарских дрожжей значительно больше и показывает более сложную динамику, чем сеть экспрессии генов у кишечной палочки.

А теперь самое интересное — создание математической модели. Ученые выбрали два варианта модели: множество Мандельброта и множество в виде вейвлетовых диадических деревьев.

Используя ранее полученные показатели коэффициента Гёльдера в мультифрактальном спектре, ученые обнаружили, что только 0.04 из всех пар ген-ФТ в сети регуляции генов пекарских дрожжей можно смоделировать используя множество Мандельброта. А у кишечной палочки вообще ни одной пары нельзя смоделировать этим методом.

Если же рассматривать те пары, что удалось смоделировать, то наблюдалось огромное расхождение в данных между моделью и экспериментальными наблюдениями. Как вывод — метод моделирования за счет множества Мандельброта не подходит.


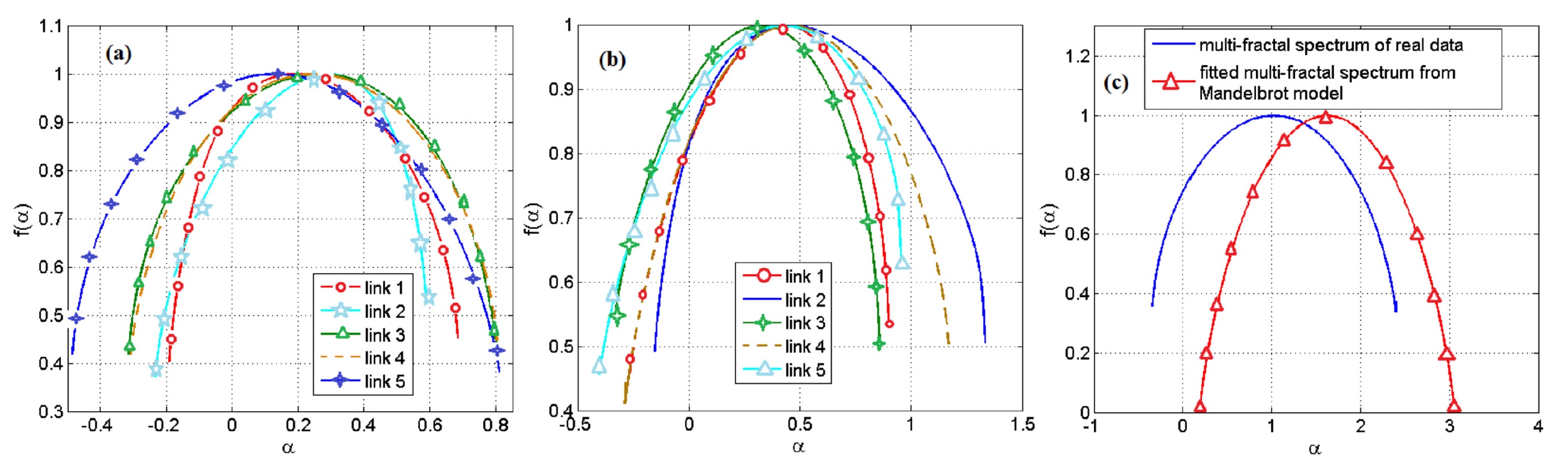
Изображение №4

Результаты использования модели на базе множества Мандельброта показаны на графиках выше. Самым ярким является 4с, где мы можем видеть насколько сильно расходятся данные.

Также ученые провели сопоставление наблюдаемой мультифрактальности взаимозависимостей в сети регуляции генов и мультифрактальной моделью случайных каскадов на вейвлет-диадических деревьях.

Исследователи решили проверить подойдет ли логарифмическая модель W-каскада для репрезентации пар ген-ФТ в сетях регуляции генов. На базе эмпирического спектра и спектра сингулярностей были вычислены параметры данной модели. Далее были проведены расчеты областей пересечения расчетного и эмпирического мультифрактальных спектров, соотношение которых и стало основным критерием для принятия или отклонения данной математической мультифрактальной модели.


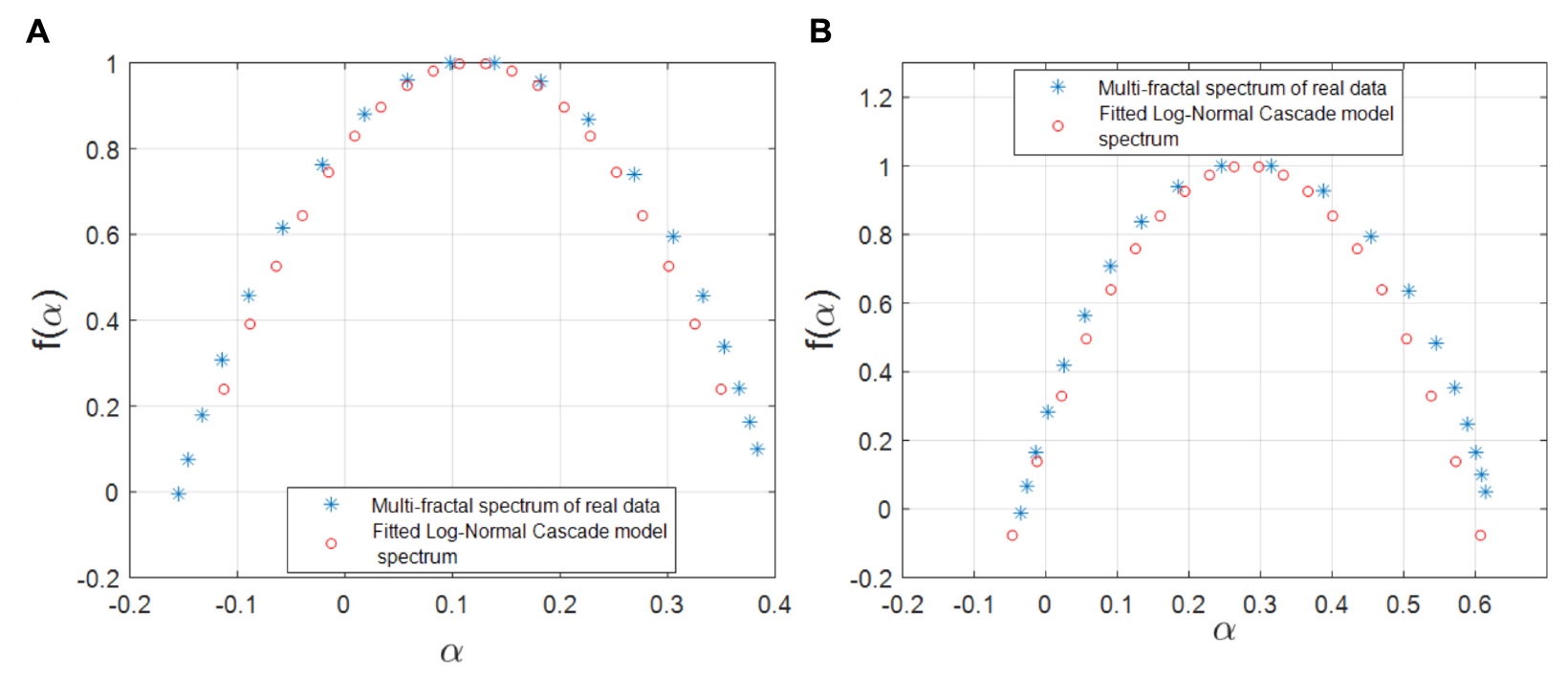
Изображение №5

Как видно из графиков выше, демонстрирующих смоделированные и эмпирические мультифрактальные спектры, данная модель практически полностью соотносится с данными наблюдений и расчетов, проведенных ранее.

Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад исследовательской группы по этой ссылке.

Эпилог

Данное исследование, будучи по большей степени теоретическим, имеет большой потенциал практического применения, поскольку помогло математически смоделировать сеть регуляции экспрессии генов — одного из самых важных процессов в любом живом организме. Сложные процессы сложно понять, как бы странно это не звучало. Дабы облегчить себе задачу, необходимо разделить процесс на составляющие, составить их «карты», и следовать по нужному маршруту, отмечая все важные особенности и характеристики. Математическое моделирование как ничто другое отлично подходит для этого. Изучив математическую модель объекта или процесса, мы может понять с чем имеем дело, прежде чем приступать к исследованию фактического объекта или процесса.

Это исследование лишний раз подтвердило, что далеко не только физика и химия правят миром, но и математика занимает далеко не последнее место на Олимпе наук.

Благодарю за внимание, оставайтесь любопытствующими и отличной вам рабочей недели, ребята.

Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас оформив заказ или порекомендовав знакомым, 30% скидка для пользователей Хабра на уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps от $20 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps до 1 января бесплатно при оплате на срок от полугода, заказать можно тут.

Dell R730xd в 2 раза дешевле? Только у нас 2 х Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 ТВ от $249 в Нидерландах и США! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?