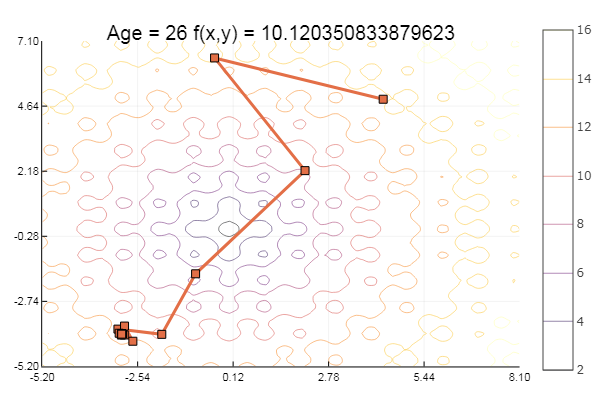
Продолжаем знакомство с методами многомерной оптимизации.
Далее предложена реализация метода наискорейшего спуска с анализом скорости выполнения, а также имплементация метода Нелдера-Мида средствами языка Julia и C++.
Метод градиентного спуска
Поиск экстремума ведется шагами в направлении градиента (max) или антиградиента (min). На каждом шаге в направлении градиента (антиградиента) движение осуществляется до тех пор, пока функция возрастает (убывает).
За теорией пройдитесь по ссылкам:
- Градиентный спуск
- Метод сопряжённых градиентов
- Метод Нелдера-Мида
- Обзор градиентных методов
- SciPy, оптимизация
- Обзор основных методов математической оптимизации для задач с ограничениями
- Метод оптимизации Нелдера — Мида. Реализация на Python
- Зайцев В. В. Численные методы для физиков. Нелинейные уравнения и оптимизация
В качестве основы были использованы примеры из последнего источника.
Модельной функцией выберем эллиптический параболоид и зададим функцию отрисовки рельефа:
using Plots
plotly() # интерактивные графики
function plotter(plot_fun; low, up)
Xs = range(low[1], stop = up[1], length = 80)
Ys = range(low[2], stop = up[2], length = 80)
Zs = [ fun([x y]) for x in Xs, y in Ys ];
plot_fun(Xs, Ys, Zs)
xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) # линовка осей
yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] )
end
parabol(x) = sum(u->u*u, x) # сумма квадратов
fun = parabol
plotter(surface, low = [-1 -1], up = [1 1])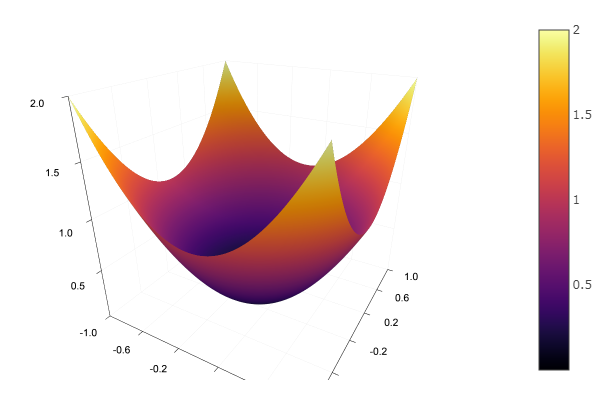
Зададим функцию реализующую метод наискорейшего спуска, которая принимает размерность задачи, точность, длину шага, начальное приближение и размеры рамки ограничивающей график:
# точка-с-запятой значит, что все последующие параметры - ключевые слова
function ofGradient(; ndimes = 2, ? = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10])
k = 0
while st > ?
g = grad(fit, 0.01)
fung = fun(fit)
fit -= st*g
if fun(fit) >= fung
st *= 0.5
fit += st*g
end
k += 1
#println(k, " ", fit)
end
#println(fun(fit))
endНа функции вычисляющей направление градиента можно заостриться в плане оптимизации.
Первое, что идет на ум — это действия с матрицами:
# \delta - приращение аргумента используемое для вычисления
# производных по формуле центральных разностей
function grad(fit, ?)
ndimes = length(fit)
? = zeros(ndimes, ndimes)
for i = 1:ndimes
?[i,i] = ?
end
fr = [ fun( fit + ?[:,i] ) for i=1:ndimes]
fl = [ fun( fit - ?[:,i] ) for i=1:ndimes]
g = 0.5(fr - fl)/?
modg = sqrt( sum(x -> x*x, g) )
g /= modg
endЧем действительна хороша Julia, так это тем, что проблемные места легко можно потестить:
#]add BenchmarkTools
using BenchmarkTools
@benchmark ofGradient()
BenchmarkTools.Trial:
memory estimate: 44.14 KiB
allocs estimate: 738
--------------
minimum time: 76.973 ?s (0.00% GC)
median time: 81.315 ?s (0.00% GC)
mean time: 92.828 ?s (9.14% GC)
maximum time: 5.072 ms (94.37% GC)
--------------
samples: 10000
evals/sample: 1Можно кинуться перепечатывать всё в Сишном стиле
function grad(fit::Array{Float64,1}, ?::Float64)
ndimes::Int8 = 2
g = zeros(ndimes)
modg::Float64 = 0.
Fr::Float64 = 0.
Fl::Float64 = 0.
for i = 1:ndimes
fit[i] += ?
Fr = fun(fit)
fit[i] -= 2?
Fl = fun(fit)
fit[i] += ?
g[i] = 0.5(Fr - Fl)/?
modg += g[i]*g[i]
end
modg = sqrt( modg )
g /= modg
end
@benchmark ofGradient()
BenchmarkTools.Trial:
memory estimate: 14.06 KiB
allocs estimate: 325
--------------
minimum time: 29.210 ?s (0.00% GC)
median time: 30.395 ?s (0.00% GC)
mean time: 33.603 ?s (6.88% GC)
maximum time: 4.287 ms (98.88% GC)
--------------
samples: 10000
evals/sample: 1Но как оказывается, оно само и без нас знает, какие типы надо ставить, так что приходим к компромиссу:
function grad(fit, ?) # вычисляет направление градиента
ndimes = length(fit)
g = zeros(ndimes)
for i = 1:ndimes
fit[i] += ?
Fr = fun(fit)
fit[i] -= ?
fit[i] -= ?
Fl = fun(fit)
fit[i] += ?
g[i] = 0.5(Fr - Fl)/?
end
modg = sqrt( sum(x -> x*x, g) )
g /= modg
end
@benchmark ofGradient()
BenchmarkTools.Trial:
memory estimate: 15.38 KiB
allocs estimate: 409
--------------
minimum time: 28.026 ?s (0.00% GC)
median time: 30.394 ?s (0.00% GC)
mean time: 33.724 ?s (6.29% GC)
maximum time: 3.736 ms (98.72% GC)
--------------
samples: 10000
evals/sample: 1А теперь пусть рисует:
function ofGradient(; ndimes = 2, ? = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10])
k = 0
x = []
y = []
push!(x, fit[1])
push!(y, fit[2])
plotter(contour, low = low, up = up)
while st > ?
g = grad(fit, 0.01)
fung = fun(fit)
fit -= st*g
if fun(fit) >= fung
st *= 0.5
fit += st*g
end
k += 1
#println(k, " ", fit)
push!(x, fit[1])
push!(y, fit[2])
end
plot!(x, y, w = 3, legend = false, marker = :rect )
title!("Age = $k f(x,y) = $(fun(fit))")
println(fun(fit))
end
ofGradient()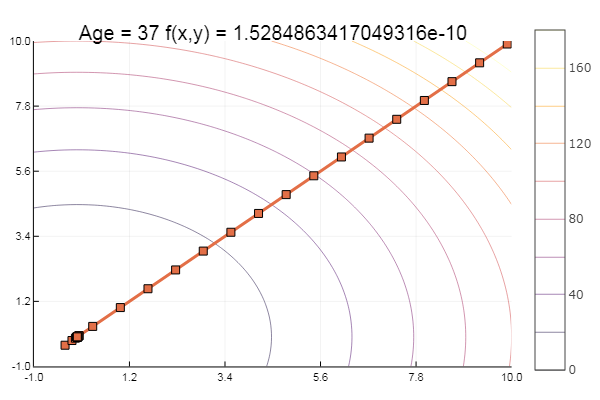
А теперь опробуем на функции Экли:
ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ?
# f(0,0) = 0, x_i ? [-5,5]
fun = ekly
ofGradient(fit = [4.3, 4.9], st = 0.1, low = [3 4.5], up = [4.5 5.4] )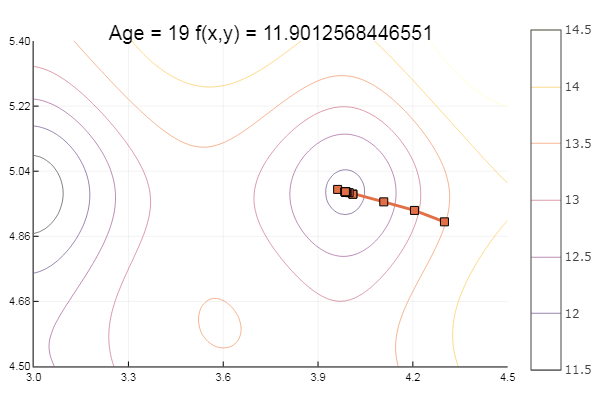
Свалилось в локальный минимум. Сделаем-ка шаги побольше:
ofGradient(fit = [4.3, 4.9], st = 0.9, low = [3 4.5], up = [4.5 5.4] )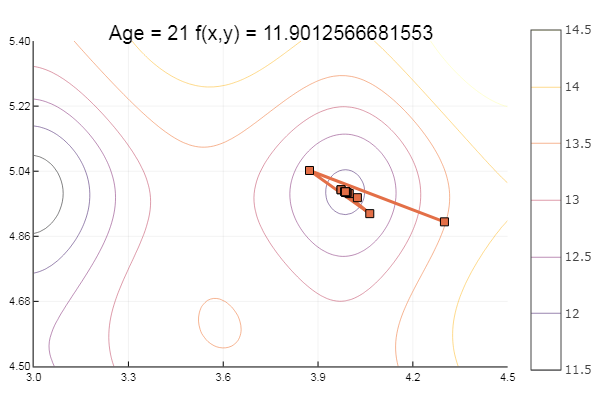
ofGradient(fit = [4.3, 4.9], st = 1.9, low = [-5.2 -2.2], up = [8.1 7.1] )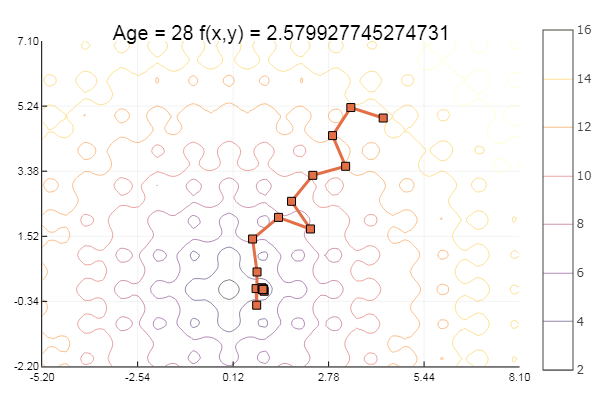
… и еще немного:
ofGradient(fit = [4.3, 4.9], st = 8.9, low = [-5.2 -2.2], up = [8.1 7.1] )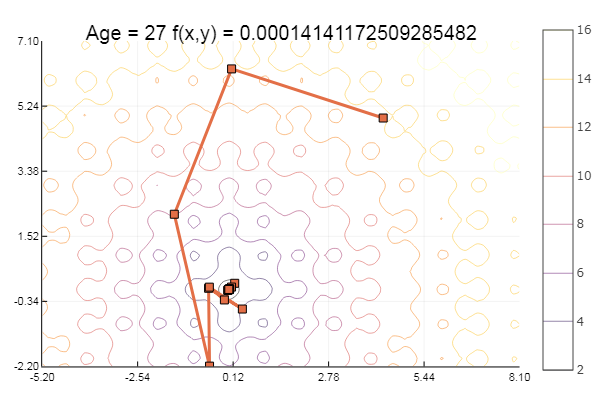
Отлично! А теперь что-нибудь с оврагом, например функцию Розенброка:
rosenbrok(x) = 100(x[2]-x[1]*x[1])^2 + (x[1]-1)^2
# f(0,0) = 0, x_i ? [-5,5]
fun = rosenbrok
plotter(surface, low = [-2 -1.5], up = [2 1.5])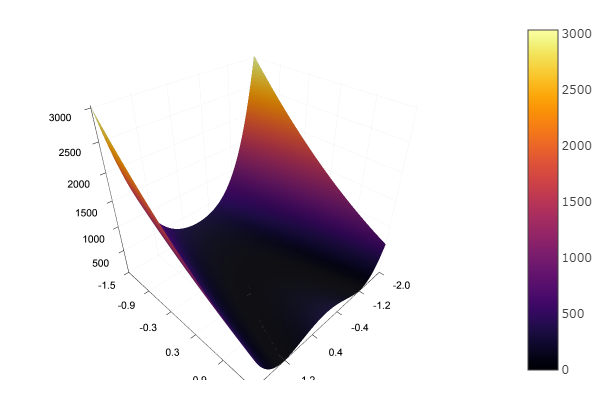
ofGradient(fit = [2.3, 2.2], st = 9.9, low = [-5.2 -5.2], up = [8.1 7.1] )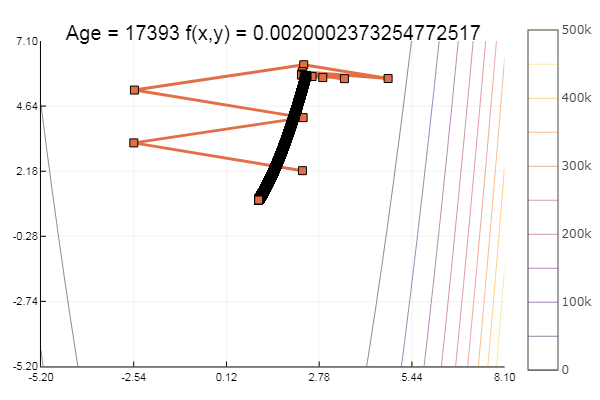
ofGradient(fit = [2.3, 2.2], st = 0.9, low = [-5.2 -5.2], up = [8.1 7.1] )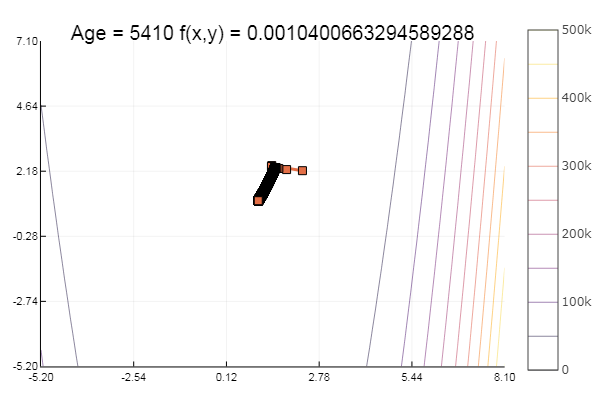
Мораль: градиенты не любят пологостей.
Симплекс метод
Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной(точнее — градиентов) функции, а поэтому легко применим к негладким и/или зашумлённым функциям.
Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума.
Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс.
Вспомогательные функции:
#сортировка столбцов матрицы выстраиванием элементов последней строки в порядке возрастания
function sortcoord(Mx)
N = size(Mx,2)
f = [fun(Mx[:,i]) for i in 1:N] # значение функции в вершинах
Mx[:, sortperm(f)]
#Return a permutation vector I that puts v[I] in sorted order.
end
# Норма матрицы
function normx(Mx)
m = size(Mx,2)
D = zeros(m-1,m)
vecl(x) = sqrt( sum(u -> u*u, x) )# длина вектора
for i = 1:m, j = i+1:m
D[i,j] = vecl(Mx[:,i] - Mx[:,j]) # считает длину разности столбцов
end
D
sqrt(maximum(D))
end
function simplexplot(xy, low, up)
for i = 1:length(xy)
if i%11 == 0
low *= 0.05
up *= 0.05
end
Xs = range(low[1], stop = up[1], length = 80)
Ys = range(low[2], stop = up[2], length = 80)
Zs = [ fun([x y]) for y in Ys, x in Xs ]
contour(Xs, Ys, Zs)
xaxis!( low[1]:(up[1]-low[1])*0.2:up[1] )
yaxis!( low[2]:(up[2]-low[2])*0.2:up[2] )
plot!(xy[i][1,:], xy[i][2,:], w = 3, legend = false, marker = :circle )
title!("Age = $i f(x,y) = $(fun(xy[i][:,1]))")
savefig("$fun $i.png")
end
endИ сам симплекс метод:
function ofNelderMid(; ndimes = 2, ? = 1e-4, fit = [.1, .1], low = [-1 -1], up = [1 1])
vecl(v) = sqrt( sum(x -> x*x, v) )
k = 0
N = ndimes
dz = zeros(N, N+1)
Xx = zeros(N, N+1)
coords = []
for i = 1:N+1
Xx[:,i] = fit
end
for i = 1:N
dz[i,i] = 0.5*vecl(fit)
end
Xx += dz
p = normx(Xx)
while p > ?
k += 1
Xx = sortcoord(Xx)
Xo = [ sum(Xx[i,1:N])/N for i = 1:N ] # среднее эл-тов i-й строки
Ro = 2Xo - Xx[:,N+1]
FR = fun(Ro)
if FR > fun(Xx[:,N+1])
for i = 2:N+1
Xx[:,i] = 0.5(Xx[:,1] + Xx[:,i])
end
else
if FR < fun(Xx[:,1])
Eo = Xo + 2(Xo - Xx[:,N+1])
if FR > fun(Eo)
Xx[:,N+1] = Eo
else
Xx[:,N+1] = Ro
end
else
if FR <= fun(Xx[:,N])
Xx[:,N+1] = Ro
else
Co = Xo + 0.5(Xo - Xx[:,N+1])
if FR > fun(Co)
Xx[:,N+1] = Co
else
Xx[:,N+1] = Ro
end
end
end
end
#println(k, " ", p, " ", Xx[:,1])
push!(coords, [Xx[:,1:3] Xx[:,1] ])
p = normx(Xx)
end #while
#simplexplot(coords, low, up)
fit = Xx[:,1]
end
ofNelderMid(fit = [-9, -2], low = [-2 2], up = [-8 8])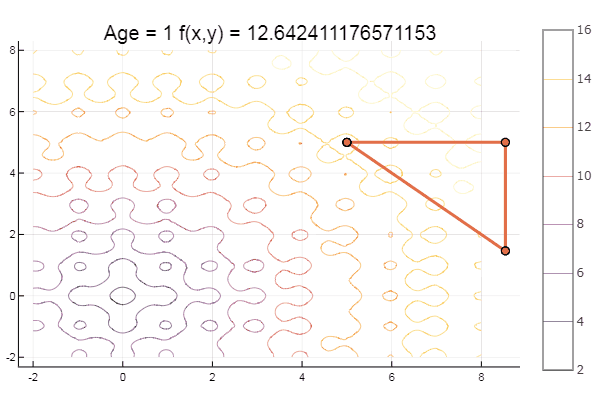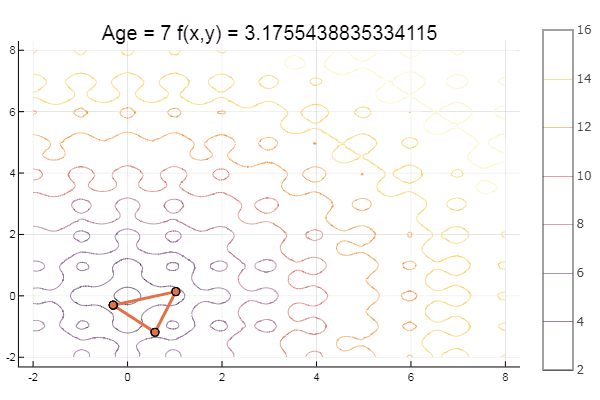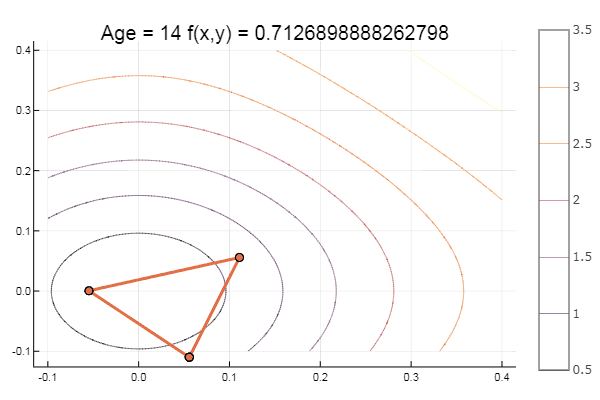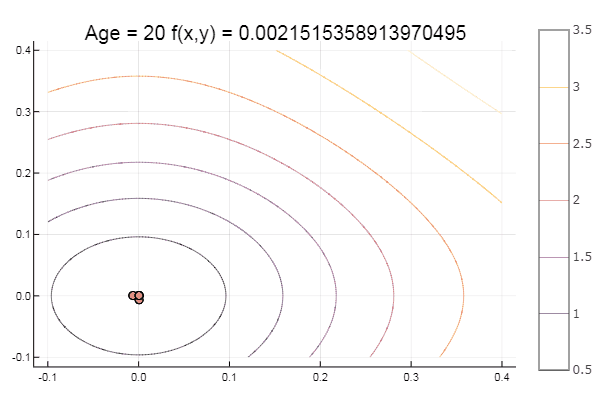
И на десерт какую-нибудь буку… например функцию Букина
bukin6(x) = 100sqrt(abs(x[2]-0.01x[1]*x[1])) + 0.01abs(x[1]+10)
# f(-10,1) = 0, x_i ? [-15,-5; -3,3]
fun = bukin6
ofNelderMid(fit = [-10, -2], low = [-3 -7], up = [-8 -4.5])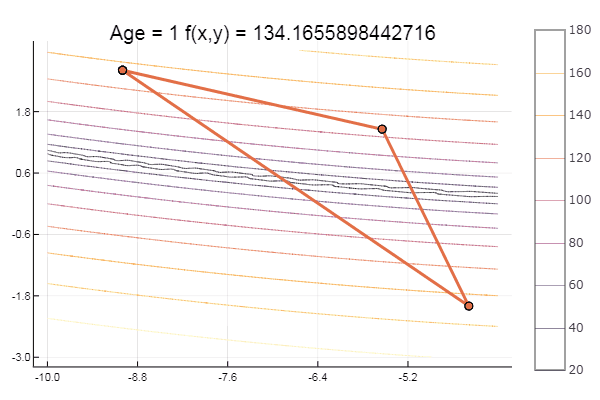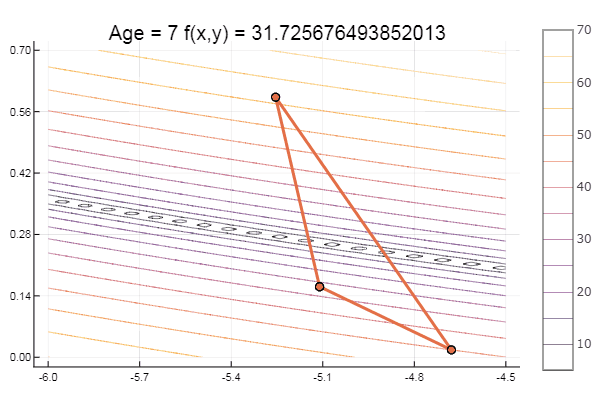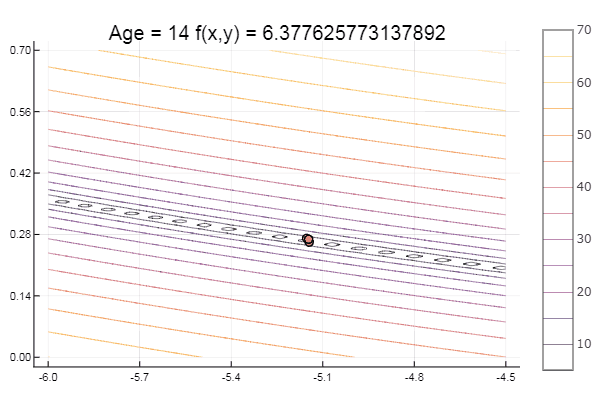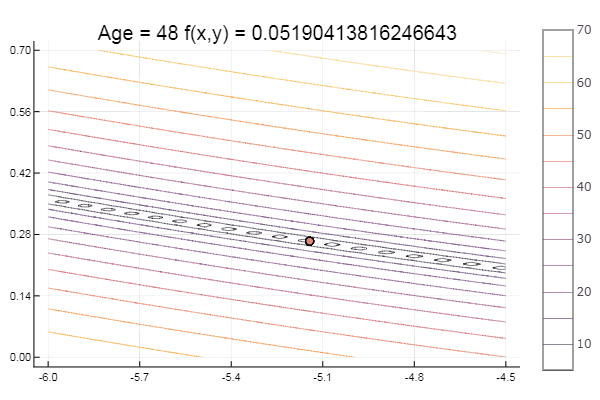
Локальный минимум — ну ничего, главное правильно подобрать стартовый симплекс, так что для себя я нашел фаворита.
Бонус. Методы Нелдера-Мида, наискорейшего спуска и покоординатного спуска на С++
/*
* File: main.cpp
* Author: User
*
* Created on 3 сентября 2017 г., 21:22
*/
#include <iostream>
#include <math.h>
using namespace std;
typedef double D;
class Model
{
public:
D *fit;
D ps;
Model();
D I();
};
Model :: Model()
{
ps = 1;
fit = new D[3];
fit[0]=1.3;
fit[1]=1.;
fit[2]=2.;
}
D Model :: I() // rosenbrock
{
return 100*(fit[1]-fit[0]*fit[0]) * (fit[1]-fit[0]*fit[0]) + (1-fit[0])*(1-fit[0]);
}
class Methods : public Model
{
public:
void ofDescent();
void Newton(int i);
void SPI(int i); //sequential parabolic interpolation
void Cutters(int i);
void Interval(D *ab, D st, int i);
void Gold_section(int i);
void ofGradient();
void Grad(int N, D *g, D delta);
void Srt(D **X, int N);
void ofNelder_Mid();
D Nor(D **X, int N);
};
void Methods :: ofDescent()//метод покоординатного спуска
{
int i, j=0;
D *z = new D[3];
D sumx, sumz;
sumx = sumz = 0;
do
{
sumx = sumz = 0;
for(i=0; i<3; i++)
z[i] = fit[i];
for(i=0; i<2; i++)
{
//Cutters(i);
//SPI(i);
Newton(i);
//Gold_section(i);
sumx += fit[i];
sumz += z[i];
}
j++;
//if(j%1000==0)
cout << j << " " << fit[0] << " " << fit[1] << " " << fit[2] << " " << fit[3] << endl;
//cout << sumz << " " << sumx << endl;
}
while(fabs(sumz - sumx) > 1e-6);
delete[]z;
}
void Methods :: SPI(int i)
{
int k = 2;
D f0, f1, f2;
D v0, v1, v2;
D s0, s1, s2;
D *X = new D[300];
X[0] = fit[i] + 0.01;
X[1] = fit[i];
X[2] = fit[i] - 0.01;
while(fabs(X[k] - X[k-1]) > 1e-3)
{
fit[i] = X[k];
f0 = I();
fit[i] = X[k-1];
f1 = I();
fit[i] = X[k-2];
f2 = I();
v0 = X[k-1] - X[k-2];
v1 = X[k ] - X[k-2];
v2 = X[k ] - X[k-1];
s0 = X[k-1]*X[k-1] - X[k-2]*X[k-2];
s1 = X[k ]*X[k ] - X[k-2]*X[k-2];
s2 = X[k ]*X[k ] - X[k-1]*X[k-1];
X[k+1] = 0.5*(f2*s2 - f1*s1 + f0*s0) / (f2*v2 - f1*v1 + f0*v0);
k++;
cout << k << " " << X[k] << endl;
}
fit[i] = X[k];
delete[]X;
}
void Methods :: Newton(int i)
{
D dt, T, It;
int k=0;
while(fabs(T-fit[i]) > 1e-3)
{
It = I();
T = fit[i];
fit[i] += 0.01;
dt = I();
fit[i] -= 0.01;
fit[i] -= It*0.001 / (dt - It);
cout << k << " " << fit[i] << endl;
k++;
}
}
void Methods :: Cutters(int i)
{
D Tn, Tnm, Tnp, It, Itm;
int j=0;
Tn = 0.15;
Tnm = 2.65;//otrezok
Itm = I();
//cout << Tnm << " " << Tn << endl;
while(fabs(Tn-Tnm) > 1e-6)
{
fit[i] = Tn;
It = I();
Tnp = Tn - It * (Tn-Tnm) / (It-Itm);
cout << j+1 << " " << Tnp << endl;
Itm = It;
Tnm = Tn;
Tn = Tnp;
j++;
}
fit[i] = Tnp;
}
void Methods :: Interval(D *ab, D st, int i)
{
D Fa, Fdx, d, c, Fb, fitbox = fit[i];
ab[0] = fit[i];
Fa = I();
fit[i] -= st;
Fdx = I();
fit[i] += st;
if(Fdx < Fa)
st = -st;
fit[i] += st;
ab[1] = fit[i];
Fb = I();
while(Fb < Fa)
{
d = ab[0];
ab[0] = ab[1];
Fa = Fb;
fit[i] += st;
ab[1] = fit[i];
Fb = I();
cout << Fb << " " << Fa << endl;
}
if(st<0)
{
c = ab[1];
ab[1] = d;
d = c;
}
ab[0] = d;
fit[i] = fitbox;
}
void Methods :: Gold_section(int i)
{
D Fa, Fb, al, be;
D *ab = new D[2];
D st = 0.5;
D e = 0.5*(sqrt(5) - 1);
Interval(ab, st, i);
al = e*ab[0] + (1-e)*ab[1];
be = e*ab[1] + (1-e)*ab[0];
fit[i] = al;
Fa = I();
fit[i] = be;
Fb = I();
while(fabs(ab[1]-ab[0]) > e)
{
if(Fa < Fb)
{
ab[1] = be;
be = al;
Fb = Fa;
al = e*ab[0] + (1-e)*ab[1];
fit[i] = al;
Fa = I();
}
if(Fa > Fb)
{
ab[0] = al;
al = be;
Fa = Fb;
be = e*ab[1] + (1-e)*ab[0];
fit[i] = be;
Fb = I();
}
cout << ab[0] << " " << ab[1] << endl;
}
fit[i] = 0.5*(ab[0] + ab[1]);
cout << ab[0] << " " << ab[1] << endl;
}
void Methods :: Grad(int N, D *g, D delta)//вектор направления градиента
{
int n;
D Fr, Fl, modG=0;
for(n=0; n<N; n++)
{
fit[n] += delta;
Fr = I();
fit[n] -= delta;
fit[n] -= delta;
Fl = I();
fit[n] += delta;
g[n] = (Fr - Fl)*0.5/delta;
modG += g[n]*g[n];
}
modG = sqrt(modG);
for(n=0; n<N; n++)
g[n] /= modG;
g[N] = I();
}
void Methods :: ofGradient()
{
int n, j=0;
D Fun, st, eps;
const int N = 2;
D *g = new D[N+1];
st = 0.1;
eps = 0.000001;
while(st > eps)
{
Grad(N,g,0.0001);
for(n=0; n<N; n++)
fit[n] -= st*g[n];
Fun = I();
if(Fun >= g[N])
{
st /= 2.;
for(n=0; n<N; n++)
fit[n] += st*g[n];
}
j++;
cout << j << " " << fit[0]/ps << " " << fit[1]/ps << " " << fit[2]/ps<< endl;
}
}
void Methods :: ofNelder_Mid()
{
int i, j, k;
D modz = 0., p, eps = 1e-3;
D FR, FN, F0, FE, FNm1, FC;
const int N = 2;
D *Co = new D[N];
D *Eo = new D[N];
D *Ro = new D[N];
D *Xo = new D[N];
D **Xx = new D*[N];
D **dz = new D*[N];
for(i=0;i<N;i++)
{
dz[i] = new D[N];
Xx[i] = new D[N+1];
}
for(i=0;i<N;i++)
for(j=0;j<N;j++)
if(i^j)
dz[i][j] = 0;
else
dz[i][j] = 1;
for(i=0;i<N;i++)
Xx[i][N] = fit[i];
for(i=0;i<N;i++)
modz += fit[i]*fit[i];
modz = sqrt(modz);
for(i=0;i<N;i++)
dz[i][i] = 0.5*modz;
for(i=0;i<N;i++)
for(j=0;j<N;j++)
Xx[i][j] = fit[i] + dz[i][j];
k = 0;
p = Nor(Xx, N);
while(p > eps)
{
k++;
Srt(Xx, N);
for(i=0;i<N;i++)
Xo[i] = 0.;
for(i=0;i<N;i++)
for(j=0;j<N;j++)
Xo[i] += Xx[i][j];
for(i=0;i<N;i++)
Xo[i] /= N;
for(i=0;i<N;i++)
Ro[i] = Xo[i] + (Xo[i]-Xx[i][N]);
for(i=0;i<N;i++)
fit[i] = Ro[i];
FR = I();
for(i=0;i<N;i++)
fit[i] = Xx[i][N];
FN = I();
if(FR > FN)
{
for(i=0;i<N;i++)
for(j=1;j<=N;j++)
Xx[i][j] = 0.5*(Xx[i][0] + Xx[i][j]);
}
else
{
for(i=0;i<N;i++)
fit[i] = Xx[i][0];
F0 = I();
if(FR < F0)
{
for(i=0;i<N;i++)
Eo[i] = Xo[i] +2*(Xo[i] - Xx[i][N]);
for(i=0;i<N;i++)
fit[i] = Eo[i];
FE = I();
if(FE < FR)
for(i=0;i<N;i++)
Xx[i][N] = Eo[i];
else
for(i=0;i<N;i++)
Xx[i][N] = Ro[i];
}
else
{
for(i=0;i<N;i++)
fit[i] = Xx[i][N-1];
FNm1 = I();
if(FR <= FNm1)
for(i=0;i<N;i++)
Xx[i][N] = Ro[i];
else
{
for(i=0;i<N;i++)
Co[i] = Xo[i] +0.5*(Xo[i] - Xx[i][N]);
for(i=0;i<N;i++)
fit[i] = Co[i];
FC = I();
if(FC < FR)
for(i=0;i<N;i++)
Xx[i][N] = Co[i];
else
for(i=0;i<N;i++)
Xx[i][N] = Ro[i];
}
}
}
for(i=0;i<N;i++)
cout << Xx[i][0] << " ";
cout << k << " " << p << endl;
p = Nor(Xx, N);
if(p < eps)
break;
}
for(i=0;i<N;i++)
fit[i] = Xx[i][0];
/*for(i=0;i<N;i++)
{
for(j=0;j<N+1;j++)
cout << Xx[i][j] << " ";
cout << endl;
}*/
delete[]Co;
delete[]Xo;
delete[]Ro;
delete[]Eo;
for(i=0;i<N;i++)
{
delete[]dz[i];
delete[]Xx[i];
}
}
//возвращает норму вектора
D Methods :: Nor(D **X, int N)
{
int i, j, k;
D norm, xij, pn = 0.;
for(i=0;i<N;i++)
for(j=i+1;j<=N;j++)
{
xij = 0.;
for(k=0;k<N;k++)
xij += ( (X[k][i]-X[k][j])*(X[k][i]-X[k][j]) );
pn = sqrt(xij);//считает длину разности столбцов
if(norm > pn)
norm = pn;//ищет максимальную длину
}
return sqrt(norm);
}
//сортировка координат вершин симплекса
void Methods :: Srt(D **X, int N)
{
int i, j, k;
D temp;
D *f = new D[N+1];
D *box = new D[N];
D **y = new D*[N+1];
for(i=0;i<N+1;i++)//динамическая память
y[i] = new D[N+1];
for(i=0;i<N;i++)
box[i] = fit[i];//старые тау в коробку
for(i=0;i<=N;i++)
{
for(j=0;j<N;j++)
fit[j] = X[j][i];
f[i] = I();//значения функции в вершинах симплекса
}
for(i=0;i<N;i++)
fit[i] = box[i];//выкладывает тау из коробки
for(i=0;i<N;i++)
for(j=0;j<=N;j++)
y[i][j] = X[i][j];
for(i=0;i<=N;i++)
y[N][i] = f[i];//stack(X, f)
//Сортирует столбцы матрицы таким образом,
//чтобы расположить элементы в строке N в порядке возрастания
for(i=1;i<=N;i++)
for(j=0;j<=N-i;j++)
if(y[N][j] >= y[N][j+1])
for(k=0;k<=N;k++)
{
temp = y[k][j];
y[k][j] = y[k][j+1];
y[k][j+1] = temp;
}
//submatrix вырезает отсортированное
for(i=0;i<N;i++)
for(j=0;j<=N;j++)
X[i][j] = y[i][j];
/*
for(i=0;i<=N;i++)
{
for(j=0;j<=N;j++)
cout << y[i][j] << " ";
cout << endl;
}
*/
for(i=0;i<N+1;i++)
delete[]y[i];
delete[]box;
delete[]f;
}
int main()
{
Methods method;
//method.ofDescent();
//method.ofGradient();
method.ofNelder_Mid();
return 0;
}
На сегодня достаточно. Следующим этапом будет логично попробовать что-нибудь из глобальной оптимизации, набрать побольше тестовых функций, а затем изучить пакеты со встроенными методами.
Комментарии (8)

kosmonaFFFt
13.02.2019 13:04Немного из глобальной оптимизации, что можно попробовать:
elib.bsu.by/bitstream/123456789/111836/1/%D0%A0%D1%83%D0%B1%D0%B0%D0%BD.pdf
red_b
14.02.2019 08:25Неплохой алгоритм. Проводим сейчас разные его исследования под руководством изобретателя метода. Хорошо показывает себя при наличии сильных помех. Только алгоритмы глобальной оптимизации нужно и испытывать на многоэкстремальных функциях. Например конструировать их по методу Бочарова-Фельдбаума, писал давненько об этом на хабре. Удобный метод. Если интересна реализация этого алгоритма, то она на гитхабе.

ProLimit
13.02.2019 13:26Спасибо за статью и знакомство с методом Нелдера-Мида, как раз решаю задачу оптимизации и попробую его. Вопрос: так все таки он может находить глобальные минимумы в случае множества локальных? Что нужно учесть в его настройке для повышения вероятности нахождения глобального минимума?

Yermack Автор
13.02.2019 13:58В приведенной реализации ничего не настраивается, как, например длина шага и варьирование в градиентном спуске. Для функции одной-трех переменных можно построить рельеф, чтоб как то всё отслеживать, а вот когда переменных много, то тут только разные начальные значения пробовать. Я начал рассматривать метод роя частиц и по мне, так неплохо пробовать искать глобальный минимум чем то вроде него, а затем уточнять с помощь симплекса. Меня как студента пока интересует оптимизация ради оптимизации, а уж когда встанет задача, где минимизация будет лишь средством, можно будет воспользоваться чем-нибудь из пакетов — там куча понтовых методов с трудновыговариваемыми названиями, до них дело тоже дойдет

ProLimit
13.02.2019 14:57Иногда приходится самому метод реализовывать и желательно обойтись минимумом кода, например под микроконтроллеры — пакеты тут сложно использовать, они обычно тянут с собой много лишнего. Как раз простой, но эффективный метод хорошо подходит, его только надо заточить под задачу.

ProLimit
15.02.2019 13:11+1Upd: Поделюсь практическим результатом: попробовал этот метод в реальной задаче калибровки 12 параметро MEMS-сенсора путем сравнения его измерений с референсным сигналом. Работает стабильно, меньше секунды на выборке из 600 измерений (примерно 1000 итераций) на слабом железе. Под мою задачу подходит отлично.


ericgrig
Спасибо за статью!
Хочу отметить, что не стоит приводить значение функции f(x,y) с точностью до 15-го знака после запятой. Это слишком избыточно. На графиках и в тексте программы вы используете два знака после запятой, и для изложения материала этого достаточно. Вряд ли какие-либо изменения значений переменных на уровне 15-го знака повлияют на ваши суждения.