Прелюдия

Эта статья посвящена бинарным деревьям поиска. Недавно делал статью про сжатие данных методом Хаффмана. Там я не очень обращал внимание на бинарные деревья, ибо методы поиска, вставки, удаления не были актуальны. Теперь решил написать статью именно про деревья. Пожалуй, начнем.

Дерево — структура данных, состоящая из узлов, соединенных ребрами. Можно сказать, что дерево — частный случай графа. Вот пример дерева:



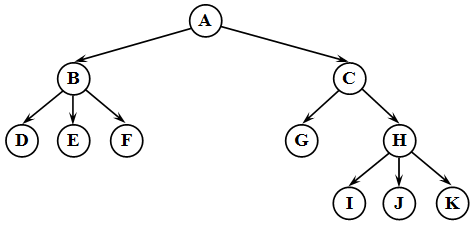
Это не бинарное дерево поиска! Все под кат!

Терминология

Корень

Корень дерева — это самый верхний его узел. В примере — это узел A. В дереве от корня к любому другому узлу может вести только один путь!

Родители/потомки

Все узлы, кроме корневого, имеют ровно одно ребро, ведущее вверх к другому узлу. Узел, расположенный выше текущего, называется родителем этого узла. Узел, расположенный ниже текущего, и соединенный с ним называется потомком этого узла. Давайте на примере. Возьмем узел B, тогда его родителем будет узел A, а потомками — узлы D, E и F.

Лист

Узел, у которого нет потомков, будет называться листом дерева. В примере листьями будут являться узлы D, E, F, G, I, J, K.

Это основная терминология. Другие понятия будут разобраны далее. Итак, бинарное дерево — дерево, в котором каждый узел будет иметь не более двух потомков. Как вы догадались, дерево из примера не будет являться бинарным, ибо узлы B и H имеют более двух потомков. Вот пример бинарного дерева:



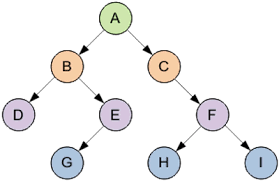
В узлах дерева может находиться любая информация. Двоичное дерево поиска — это двоичное дерево, для которого характерны следующие свойства:

1. Оба поддерева — левое и правое — являются двоичными деревьями поиска.
2. У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных самого узла X.
3. У всех узлов правого поддерева произвольного узла X значения ключей данных больше либо равны, нежели значение ключа данных самого узла X.

Ключ — какая-либо характеристика узла(например, число). Ключ нужен для того, чтобы можно было найти элемент дерева, которому соответствует этот ключ. Пример бинарного дерева поиска:

Представление дерева

По мере продвижения я буду приводить некоторые(возможно, неполные) куски кода, для того, чтобы улучшить ваше понимание. Полный код будет в конце статьи.

Дерево состоит из узлов. Структура узла:

public class Node {
    private int data;
    private Node leftChild;
    private Node rightChild;

    public Node(int newData) {
        data = newData;
    }
    //методы узла
}

Каждый узел имеет двух потомков(вполне возможно, потомки leftChild и/или rightChild будут содержать значение null). Вы, наверное, поняли, что в данном случае число data — ключ узла.

Ключ и информация в узле могут не совпадать! Например, вы могли сделать так:

public class Node {
    private int key;
    private Data myData;
    private Node leftChild;
    private Node rightChild;

    public Node(int newData) {
        data = newData;
    }
    
    public Node getLeftChild() {
        return leftChild;
    }
    public Node getRightChild() {
        return rightChild;
    }
    //методы узла
}

class Data {
    private String s;
    public Data(String s) {
         this.s = s;
    }
    public String getString() {
        return s;
    }
}

Здесь myData хранит информацию узла дерева. Важно понимать, что узел дерева может хранить любую информацию.

С узлом разобрались, теперь поговорим о проблемах насущных о деревьях. Здесь и далее под словом «дерево» буду подразумевать понятие бинарного дерева поиска. Структура бинарного дерева:

public class BinaryTree {
     private Node root;

    //методы дерева
}

Как поле класса нам понадобится только корень дерева, ибо от корня с помощью методов getLeftChild() и getRightChild() можно добраться до любого узла дерева.

Алгоритмы в дереве

Поиск

Допустим, у вас есть построенное дерево. Как найти элемент с ключом key? Нужно последовательно двигаться от корня вниз по дереву и сравнивать значение key с ключом очередного узла: если key меньше, чем ключ очередного узла, то перейти к левому потомку узла, если больше — к правому, если ключи равны — искомый узел найден! Соответствующий код:

public Node find(int findData) {
        Node current = root;
        while (current.getData() != findData) {
            if (findData < current.getData())   //идем налево
                current = current.getLeftChild();
            else    //идем направо(ситуацию равенства проверяет цикл)
                current = current.getRightChild();
            if (current == null)//если потомка не существует, значит в дереве нет элемента с ключом findData
                return null;
        }
        return current;
}

Если current становится равным null, значит, перебор достиг конца дерева(на концептуальном уровне вы находитесь в несуществующем месте дерева — потомке листа).

Рассмотрим эффективность алгоритма поиска на сбалансированном дереве(дереве, в котором узлы распределены более-менее равномерно). Тогда эффективность поиска будет O(log(n)), причем логарифм по основанию 2. Смотрите: если в сбалансированном дереве n элементов, то это значит, что будет log(n) по основанию 2 уровней дерева. А в поиске, за один шаг цикла, вы спускаетесь на один уровень.

Вставка

Если вы уловили суть поиска, то понять вставку не составит вам труда. Надо просто спуститься до листа дерева(по правилам спуска, описанным в поиске) и стать его потомком — левым, или правым, в зависимости от ключа. Реализация:

    public void insert(int insertData) {
        Node current = root;
        Node parent;//родитель текущего узла
        Node newNode = new Node(insertData);
        if (root == null)
            root = newNode;
        else {
            while (true) {
                parent = current;
                if (insertData < current.getData()) {
                    current = current.getLeftChild();
                    if (current == null) {
                         parent.setLeftChild(newNode);
                         return;
                    }
                }
                else {
                    current = current.getRightChild();
                    if (current == null) {
                        parent.setRightChild(newNode);
                        return;
                    }
                }
            }
        }
    }

В данном случае надо, помимо текущего узла, хранить информацию о родителе текущего узла. Когда current станет равным null, в переменной parent будет лежать нужный нам лист.
Эффективность вставки, очевидно, будет такой же как и у поиска — O(log(n)).

Удаление

Удаление — самая сложная операция, которую надо будет провести с деревом. Понятно, что сначала надо будет найти элемент, который мы собираемся удалять. Но что потом? Если просто присвоить его ссылке значение null, то мы потерям информацию о поддереве, корнем которого является этот узел. Методы удаления дерева разделяют на три случая.

Первый случай. Удаляемый узел не имеет потомков

Если удаляемый узел не имеет потомков, то это значит, что он является листом. Следовательно, можно просто полям leftChild или rightChild его родителя присвоить значение null. В зависимости от того, является ли удаляемый узел левым или правым потомком своего родителя, переменная isLeftChild будет принимать значение true или false соответственно.

public boolean delete(int deleteData) {
        Node current = root;
        Node parent = current;
        boolean isLeftChild = false;//информация о местоположении удаляемого листа по отношению к его родителю
        while (current.getData() != deleteData) {
            parent = current;
            if (deleteData < current.getData()) {
                current = current.getLeftChild();
                isLeftChild = true;
            } else {
                isLeftChild = false;
                current = current.getRightChild();
            }
            if (current == null)
                return false;
        }

        if (current.getLeftChild() == null && current.getRightChild() == null) {//если удаляем лист
            if (current == root)//если он корень, то достаточно сделать его равным null
                current = null;
            else if (isLeftChild)//удалем некорневой лист, являющийся
                parent.setLeftChild(null);//левым потомком своего родителя
            else
                parent.setRightChild(null);//правым потомком своего родителя
        }
        ...

Второй случай. Удаляемый узел имеет одного потомка

Этот случай тоже не очень сложный. Вернемся к нашему примеру. Допустим, надо удалить элемент с ключом 14. Согласитесь, что так как он — правый потомок узла с ключом 10, то любой его потомок(в данном случае правый) будет иметь ключ, больший 10, поэтому можно легко его «вырезать» из дерева, а родителя соединить напрямую с потомком удаляемого узла, т.е. узел с ключом 10 соединить с узлом 13. Аналогичной была бы ситуация, если бы надо было удалить узел, который является левым потомком своего родителя. Подумайте об этом сами — точная аналогия.

Код:

         //продолжение метода delete
        else if (current.getRightChild() == null) {//Если удаляемый узел имеет левого потомка
            if (current == root)//удаляемый узел - корень
                root = current.getLeftChild();//сделать корнем его (единственный) левый потомок
            else if (isLeftChild)//Если удаляемый узел является
                parent.setLeftChild(current.getLeftChild());//левым потомком своего родителя
            else
                current.setRightChild(current.getLeftChild());//правым потомком своего родителя
        } else if (current.getLeftChild() == null) {//Если удаляемый узел имеет правого потомка
            if (current == root)//удаляемый узел - корень
                root = current.getRightChild();//сделать корнем его (единственный) правый потомок
            else if (isLeftChild)//если удаляемый узел является
                parent.setLeftChild(current.getRightChild());//левым потомком своего родителя
            else
                parent.setRightChild(current.getRightChild());//правым потомком своего родителя
        }
        ...

Третий случай. Узел имеет двух потомков

Наиболее сложный случай. Разберем на новом примере.

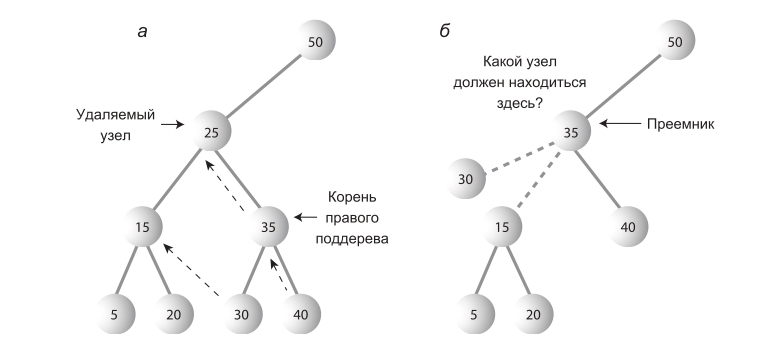
Поиск преемника

Допустим, надо удалить узел с ключом 25. Кого поставим на его место? Кто-то из его последователей(потомков или потомков потомков) должен стать преемником(тот, кто займет место удаляемого узла).

Как понять, кто должен стать преемником? Интуитивно понятно, что это узел в дереве, ключ которого — следующий по величине от удаляемого узла. Алгоритм заключается в следующем. Надо перейти к его правому потомку(всегда к правому, ибо уже говорилось, что ключ преемника больше ключа удаляемого узла), а затем пройтись по цепочке левых потомков этого правого потомка. В примере мы должны перейти к узлу с ключом 35, а затем пройтись до листа вниз по цепочке его левых потомков — в данном случае, эта цепочка состоит только из узла с ключом 30. Строго говоря, мы ищем наименьший узел в наборе узлов, больших искомого узла.



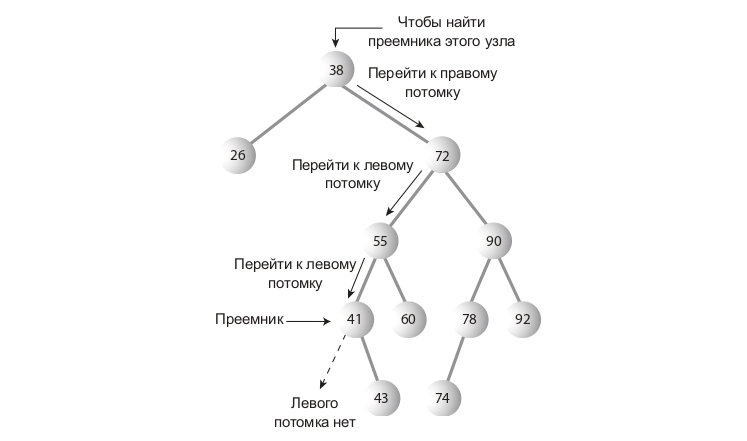
Код:

    public Node getSuccessor(Node deleteNode) {
        Node parentSuccessor = deleteNode;//родитель преемника
        Node successor = deleteNode;//преемник
        Node current = successor.getRightChild();//просто "пробегающий" узел
        while (current != null) {
            parentSuccessor = successor;
            successor = current;
            current = current.getLeftChild();
        }
        //на выходе из цикла имеем преемника и родителя преемника
        if (successor != deleteNode.getRightChild()) {//если преемник не совпадает с правым потомком удаляемого узла
            parentSuccessor.setLeftChild(successor.getRightChild());//то его родитель забирает себе потомка преемника, чтобы не потерять его
            successor.setRightChild(deleteNode.getRightChild());//связываем преемника с правым потомком удаляемого узла
        }
        return successor;
    }

Теперь можем закончить метод delete:

        //продолжение метода delete
        else {
            Node successor = getSuccessor(current);//получить преемника
            if (current == root)//если удаляемый элемент - корень дерева
                root = successor;//то сделать его преемника корнем
            else if (isLeftChild)//если удаляемый элемент является
                parent.setLeftChild(successor);//левым потомком своего родителя
            else
                parent.setRightChild(successor);//правым потомком своего родителя
        }
        return true;
    }

Полный код метода delete:

    public boolean delete(int deleteData) {
        Node current = root;
        Node parent = current;
        boolean isLeftChild = false;
        while (current.getData() != deleteData) {
            parent = current;
            if (deleteData < current.getData()) {
                current = current.getLeftChild();
                isLeftChild = true;
            } else {
                isLeftChild = false;
                current = current.getRightChild();
            }
            if (current == null)//удаляемый элемент не найден
                return false;
        }

        if (current.getLeftChild() == null && current.getRightChild() == null) {
            if (current == root)
                current = null;
            else if (isLeftChild)
                parent.setLeftChild(null);
            else
                parent.setRightChild(null);
        }
        else if (current.getRightChild() == null) {
            if (current == root)
                root = current.getLeftChild();
            else if (isLeftChild)
                parent.setLeftChild(current.getLeftChild());
            else
                current.setRightChild(current.getLeftChild());
        } else if (current.getLeftChild() == null) {
            if (current == root)
                root = current.getRightChild();
            else if (isLeftChild)
                parent.setLeftChild(current.getRightChild());
            else
                parent.setRightChild(current.getRightChild());
        } 
        else {
            Node successor = getSuccessor(current);
            if (current == root)
                root = successor;
            else if (isLeftChild)
                parent.setLeftChild(successor);
            else
                parent.setRightChild(successor);
        }
        return true;
    }

Сложность может быть аппроксимирована к O(log(n)).

Поиск максимума/минимума в дереве

Очевидно, как найти минимальное/максимальное значение в дереве — надо последовательно переходить по цепочке левых/правых элементов дерева соответственно; когда доберетесь до листа, он и будет минимальным/максимальным элементом.

    public Node getMinimum(Node startPoint) {
        Node current = startPoint;
        Node parrent = current;
        while (current != null) {
            parrent = current;
            current = current.getLeftChild();
        }
        return parrent;
    }

    public Node getMaximum(Node startPoint) {
        Node current = startPoint;
        Node parrent = current;
        while (current != null) {
            parrent = current;
            current = current.getRightChild();
        }
        return parrent;
    }

Сложность — O(log(n))

Симметричный обход

Обход — посещение каждого узла дерева с целью сделать с ним какую-то функцию.

Алгоритм рекурсивного симметричного обхода:

1. Сделать действие с левым потомком
2. Сделать действие с собой
3. Сделать действие с правым потомком

Код:

    public void inOrder(Node current) {
        if (current != null) {
            inOrder(current.getLeftChild());
            System.out.println(current.getData() + " ");//Здесь может быть все, что угодно
            inOrder(current.getRightChild());
        }
    }

Заключение

Наконец-то! Если я что-то недообъяснил или есть какие-либо замечания, то жду в комментариях. Как обещал, привожу полный код.

Node.java:

public class Node {
    private int data;
    private Node leftChild;
    private Node rightChild;

    public Node(int newData) {
        data = newData;
    }

    public void setLeftChild(Node newNode) {
        leftChild = newNode;
    }

    public void setRightChild(Node newNode) {
        rightChild = newNode;
    }

    public Node getLeftChild() {
        return leftChild;
    }

    public Node getRightChild() {
        return rightChild;
    }

    public int getData() {
        return data;
    }
}

BinaryTree.java:

public class BinaryTree {
    private Node root;

    public Node find(int findData) {
        Node current = root;
        while (current.getData() != findData) {
            if (findData < current.getData())
                current = current.getLeftChild();
            else
                current = current.getRightChild();
            if (current == null)
                return null;
        }
        return current;
    }

    public void insert(int insertData) {
        Node current = root;
        Node parrent;
        Node newNode = new Node(insertData);
        if (root == null)
            root = newNode;
        else {
            while (true) {
                parrent = current;
                if (insertData < current.getData()) {
                    current = current.getLeftChild();
                    if (current == null) {
                         parrent.setLeftChild(newNode);
                         return;
                    }
                }
                else {
                    current = current.getRightChild();
                    if (current == null) {
                        parrent.setRightChild(newNode);
                        return;
                    }
                }
            }
        }
    }

    public Node getMinimum(Node startPoint) {
        Node current = startPoint;
        Node parrent = current;
        while (current != null) {
            parrent = current;
            current = current.getLeftChild();
        }
        return parrent;
    }

    public Node getMaximum(Node startPoint) {
        Node current = startPoint;
        Node parrent = current;
        while (current != null) {
            parrent = current;
            current = current.getRightChild();
        }
        return parrent;
    }

    public Node getRoot() {
        return root;
    }

    public Node getSuccessor(Node deleteNode) {
        Node parrentSuccessor = deleteNode;
        Node successor = deleteNode;
        Node current = successor.getRightChild();
        while (current != null) {
            parrentSuccessor = successor;
            successor = current;
            current = current.getLeftChild();
        }

        if (successor != deleteNode.getRightChild()) {
            parrentSuccessor.setLeftChild(successor.getRightChild());
            successor.setRightChild(deleteNode.getRightChild());
        }
        return successor;
    }

    public boolean delete(int deleteData) {
        Node current = root;
        Node parent = current;
        boolean isLeftChild = false;
        while (current.getData() != deleteData) {
            parent = current;
            if (deleteData < current.getData()) {
                current = current.getLeftChild();
                isLeftChild = true;
            } else {
                isLeftChild = false;
                current = current.getRightChild();
            }
            if (current == null)
                return false;
        }

        if (current.getLeftChild() == null && current.getRightChild() == null) {
            if (current == root)
                current = null;
            else if (isLeftChild)
                parent.setLeftChild(null);
            else
                parent.setRightChild(null);
        }
        else if (current.getRightChild() == null) {
            if (current == root)
                root = current.getLeftChild();
            else if (isLeftChild)
                parent.setLeftChild(current.getLeftChild());
            else
                current.setRightChild(current.getLeftChild());
        } else if (current.getLeftChild() == null) {
            if (current == root)
                root = current.getRightChild();
            else if (isLeftChild)
                parent.setLeftChild(current.getRightChild());
            else
                parent.setRightChild(current.getRightChild());
        } 
        else {
            Node successor = getSuccessor(current);
            if (current == root)
                root = successor;
            else if (isLeftChild)
                parent.setLeftChild(successor);
            else
                parent.setRightChild(successor);
        }
        return true;
    }

    public void inOrder(Node current) {
        if (current != null) {
            inOrder(current.getLeftChild());
            System.out.println(current.getData() + " ");
            inOrder(current.getRightChild());
        }
    }
}

Main.java:

import java.util.Scanner;

public class Main {
    public static void main (String[] args) {
        Scanner scanner = new Scanner(System.in);

        BinaryTree binaryTree = new BinaryTree();
        int operationCommand = 0;
        int data = 0;
        while (true) {
            System.out.println("Input 1 to add element, 2 to delete, 3 to search, 4 to get max, 5 to get min, 0 to exit");
            operationCommand = scanner.nextInt();
            switch (operationCommand) {
                case 0:
                    scanner.close();
                    return;
                case 1:
                    System.out.println("Input element");
                    data = scanner.nextInt();
                    binaryTree.insert(data);
                    break;
                case 2:
                    System.out.println("Input element");
                    data = scanner.nextInt();
                    binaryTree.delete(data);
                    break;
                case 3:
                    System.out.println("Input element");
                    data = scanner.nextInt();
                    if (binaryTree.find(data) != null)
                        System.out.println("OK");
                    else
                        System.out.println("Not found");
                    break;
                case 4:
                    System.out.println(binaryTree.getMaximum(binaryTree.getRoot()));
                    break;
                case 5:
                    System.out.println(binaryTree.getMinimum(binaryTree.getRoot()));
                    break;
                default:
                    System.out.println("Another key to continue");
                    break;
            }
        }
    }
}