Вступление

В данной статье я расскажу об известном алгоритме Хаффмана, а также о его применении в сжатии данных.

В результате напишем простенький архиватор. Об этом уже была статья на Хабре, но без практической реализации. Теоретический материал текущего поста взят из школьных уроков информатики и книги Роберта Лафоре «Data Structures and Algorithms in Java». Итак, все под кат!

Немного размышлений

В обычном текстовом файле один символ кодируется 8 битами(кодировка ASCII) или 16(кодировка Unicode). Далее будем рассматривать кодировку ASCII. Для примера возьмем строку s1 = «SUSIE SAYS IT IS EASY\n». Всего в строке 22 символа, естественно, включая пробелы и символ перехода на новую строку — '\n'. Файл, содержащий данную строку будет весить 22*8 = 176 бит. Сразу же встает вопрос: рационально ли использовать все 8 бит для кодировки 1 символа? Мы ведь используем не все символы кодировки ASCII. Даже если бы и использовали, рациональней было бы самой частой букве — S — дать самый короткий возможный код, а для самой редкой букве — T (или U, или '\n') — дать код подлиннее. В этом и заключается алгоритм Хаффмана: необходимо найти оптимальный вариант кодировки, при котором файл будет минимального веса. Вполне нормально, что у разных символов длины кода будут отличаться — на этом и основан алгоритм.

Кодирование

Почему бы символу 'S' не дать код, например, длиной в 1 бит: 0 или 1. Пусть это будет 1. Тогда второму наиболее встречающемуся символу — ' '(пробел) — дадим 0. Представьте себе, вы начали декодировать свое сообщение — закодированную строку s1 — и видите, что код начинается с 1. Итак, что же делать: это символ S, или же это какой-то другой символ, например A? Поэтому возникает важное правило:

Ни один код не должен быть префиксом другого

Это правило является ключевым в алгоритме. Поэтому создание кода начинается с частотной таблицы, в которой указана частота (количество вхождений) каждого символа:

Символы с наибольшим количеством вхождений должны кодироваться наименьшим возможным количеством битов. Приведу пример одной из возможных таблиц кодов:

Таким образом, закодированное сообщение будет выглядеть так:

10 01111 10 110 1111 00 10 010 1110 10 00 110 0110 00 110 10 00 1111 010 10 1110 01110

Код каждого символа я разделил пробелом. По-настоящему в сжатом файле такого не будет!
Вытекает вопрос: как этот салага придумал код как создать таблицу кодов? Об этом пойдет речь ниже.

Построение дерева Хаффмана

Здесь приходят на выручку бинарные деревья поиска. Не волнуйтесь, здесь методы поиска, вставки и удаления не потребуются. Вот структура дерева на java:

public class Node {
    private int frequence;
    private char letter;
    private Node leftChild;
    private Node rightChild;
    ...
}

class BinaryTree {
    private Node root;

    public BinaryTree() {
        root = new Node();
    }
    public BinaryTree(Node root) {
        this.root = root;
    }
    ...
}

Это не полный код, полный код будет ниже.

Вот сам алгоритм построения дерева:

1. Создать объект Node для каждого символа из сообщения(строка s1). В нашем случае будет 9 узлов(объектов Node). Каждый узел состоит из двух полей данных: символ и частота
2. Создать объект Дерева(BinaryTree) для кажлого из узлов Node. Узел становится корнем дерева.
3. Вставить эти деревья в приоритетную очередь. Чем меньше частота, тем больше приоритет. Таким образом, при извлечении всегда выбирается дерво наименьшей частотой.

Далее нужно циклически делать следующее:

1. Извлечь два дерева из приоритетной очереди и сделать их потомками нового узла (только что созданного узла без буквы). Частота нового узла равна сумме частот двух деревьев-потомков.
2. Для этого узла создать дерево с корнем в данном узле. Вставить это дерево обратно в приоритетную очередь. (Так как у дерева новая частота, то скорее всего она встанет на новое место в очереди)
3. Продолжать выполнение шагов 1 и 2, пока в очереди не останется одно дерево — дерево Хаффмана

Рассмотрим данный алгоритм на строке s1:



Здесь символ lf(linefeed) обозначает переход на новую строку.

А что дальше?

Мы получили дерево Хаффмана. Ну окей. И что с ним делать? Его и за бесплатно не возьмут А далее, нужно отследить все возможные пути от корня до листов дерева. Условимся обозначить ребро 0, если оно ведет к левому потомку и 1 — если к правому. Строго говоря, в данных обозначениях, код символа — это путь от корня дерева до листа, содержащего этот самый символ.



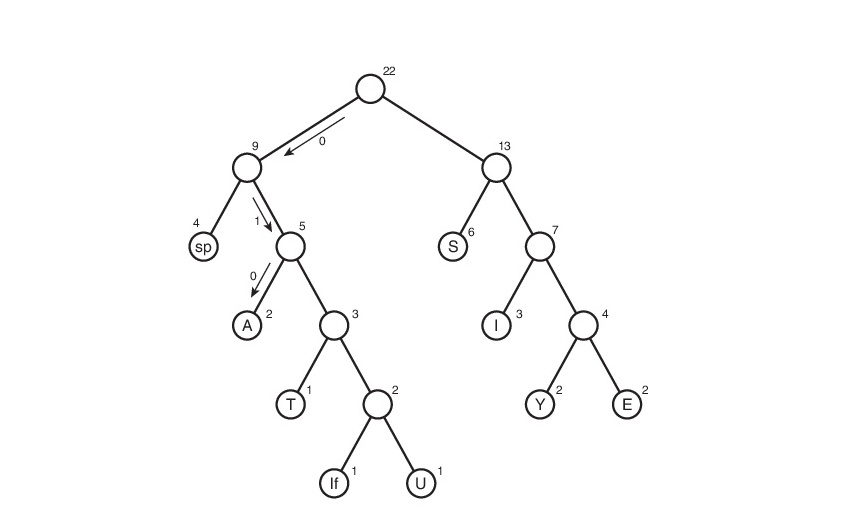
Таким макаром и получилась таблица кодов. Заметим, что если рассмотреть эту таблицу, то можно сделать вывод о «весе» каждого символа — это длина его кода. Тогда в сжатом виде исходный файл будет весить: 2 * 3 + 2*4 + 3 * 3 + 6 * 2 + 1 * 4 + 1 * 5 + 2 * 4 + 4 * 2 + 1 * 5 = 65 бит. Вначале он весил 176 бит. Следовательно, мы уменьшили его аж в 176/65 = 2.7 раза! Но это утопия. Такой коэффициент вряд ли будет получен. Почему? Об этом пойдет речь чуть позже.

Декодирование

Ну, пожалуй, осталось самое простое — декодирование. Я думаю, многие из вас догадались, что просто создать сжатый файл без каких-либо намеков на то, как он был закодирован, нельзя — мы не сможем его декодировать! Да-да, мне было тяжело это осознать, но придется создать текстовый файл table.txt с таблицей сжатия:

0100
 111
A1101
E000
I011
S10
T0101
U1100
Y001

Запись таблицы в виде 'символ'«код символа». Почему 0100 без символа? На самом деле он с символом, просто средства java, используемые мной при выводе в файл, символ перехода на новую строку — '\n' -конвертируют в переход на новую строку(как бы это глупо не звучало). Поэтому пустая строка сверху и есть символ для кода 0100. Для кода 111 символом является пробел в начале строки. Сразу скажу, что нашему коэффициенту ханаэтот способ хранения таблицы может претендовать на самый нерациональный. Но он прост для понимания и реализации. С удовольствием выслушаю Ваши рекомендации в комментариях по поводу оптимизации.

Имея эту таблицу, очень просто декодировать. Вспомним, каким правилом мы руководствовались, при создании кодировки:

Ни один код не должен являться префиксом другого

Вот тут-то оно и играет облегчающую роль. Мы читаем последовательно бит за битом и, как только полученная строка d, состоящая из прочтенных битов, совпадает с кодировкой, соответствующей символу character, мы сразу знаем что был закодирован символ character (и только он!). Далее записываем character в декодировочную строку(строку, содержащую декодированное сообщение), обнуляем строку d, и читаем дальше закодированный файл.

Реализация

Пришло время унижать мой код писать архиватор. Назовем его Compressor.

Начнем с начала. Первым делом пишем класс Node:

public class Node {
    private int frequence;//частота
    private char letter;//буква
    private Node leftChild;//левый потомок
    private Node rightChild;//правый потомок

   

    public Node(char letter, int frequence) { //собственно, конструктор
        this.letter = letter;
        this.frequence = frequence;
    }

    public Node() {}//перегрузка конструтора для безымянных узлов(см. выше в разделе о построении дерева Хаффмана)

    public void addChild(Node newNode) {//добавить потомка
        if (leftChild == null)//если левый пустой=> правый тоже=> добавляем в левый
            leftChild = newNode;
        else {
            if (leftChild.getFrequence() <= newNode.getFrequence()) //в общем, левым потомком
                rightChild = newNode;//станет тот, у кого меньше частота
            else {
                rightChild = leftChild;
                leftChild = newNode;
            }
        }

        frequence += newNode.getFrequence();//итоговая частота
    }

    public Node getLeftChild() {
        return leftChild;
    }

    public Node getRightChild() {
        return rightChild;
    }

    public int getFrequence() {
        return frequence;
    }

    public char getLetter() {
        return letter;
    }

    public boolean isLeaf() {//проверка на лист
        return leftChild == null && rightChild == null;
    }
}

Теперь деревце:

class BinaryTree {
    private Node root;

    public BinaryTree() {
        root = new Node();
    }

    public BinaryTree(Node root) {
        this.root = root;
    }

    public int getFrequence() {
        return root.getFrequence();
    }

    public Node getRoot() {
        return root;
    }
}

Приоритетная очередь:

import java.util.ArrayList;//да-да, очередь будет на базе списка

class PriorityQueue {
    private ArrayList<BinaryTree> data;//список очереди
    private int nElems;//кол-во элементов в очереди

    public PriorityQueue() {
        data = new ArrayList<BinaryTree>();
        nElems = 0;
    }

    public void insert(BinaryTree newTree) {//вставка
        if (nElems == 0)
            data.add(newTree);
        else {
            for (int i = 0; i < nElems; i++) {
                if (data.get(i).getFrequence() > newTree.getFrequence()) {//если частота вставляемого дерева меньше 
                    data.add(i, newTree);//чем част. текущего, то cдвигаем все деревья на позициях справа на 1 ячейку                   
                    break;//затем ставим новое дерево на позицию текущего
                }
                if (i == nElems - 1) 
                    data.add(newTree);
            }
        }
        nElems++;//увеличиваем кол-во элементов на 1
    }

    public BinaryTree remove() {//удаление из очереди
        BinaryTree tmp = data.get(0);//копируем удаляемый элемент
        data.remove(0);//собственно, удаляем
        nElems--;//уменьшаем кол-во элементов на 1
        return tmp;//возвращаем удаленный элемент(элемент с наименьшей частотой)
    }
}

Класс, создающий дерево Хаффмана:

public class HuffmanTree {
    private final byte ENCODING_TABLE_SIZE = 127;//длина кодировочной таблицы
    private String myString;//сообщение
    private BinaryTree huffmanTree;//дерево Хаффмана
    private int[] freqArray;//частотная таблица
    private String[] encodingArray;//кодировочная таблица


    //----------------constructor----------------------
    public HuffmanTree(String newString) {
        myString = newString;

        freqArray = new int[ENCODING_TABLE_SIZE];
        fillFrequenceArray();

        huffmanTree = getHuffmanTree();

        encodingArray = new String[ENCODING_TABLE_SIZE];
        fillEncodingArray(huffmanTree.getRoot(), "", "");
    }

    //--------------------frequence array------------------------
    private void fillFrequenceArray() {
        for (int i = 0; i < myString.length(); i++) {
            freqArray[(int)myString.charAt(i)]++;
        }
    }

    public int[] getFrequenceArray() {
        return freqArray;
    }

    //------------------------huffman tree creation------------------
    private BinaryTree getHuffmanTree() {
        PriorityQueue pq = new PriorityQueue();
        //алгоритм описан выше
        for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
            if (freqArray[i] != 0) {//если символ существует в строке
                Node newNode = new Node((char) i, freqArray[i]);//то создать для него Node
                BinaryTree newTree = new BinaryTree(newNode);//а для Node создать BinaryTree
                pq.insert(newTree);//вставить в очередь
            }
        }

        while (true) {
            BinaryTree tree1 = pq.remove();//извлечь из очереди первое дерево.

            try {
                BinaryTree tree2 = pq.remove();//извлечь из очереди второе дерево

                Node newNode = new Node();//создать новый Node
                newNode.addChild(tree1.getRoot());//сделать его потомками два извлеченных дерева
                newNode.addChild(tree2.getRoot());

                pq.insert(new BinaryTree(newNode);
            } catch (IndexOutOfBoundsException e) {//осталось одно дерево в очереди
                return tree1;
            }
        }
    }

    public BinaryTree getTree() {
        return huffmanTree;
    }

    //-------------------encoding array------------------
    void fillEncodingArray(Node node, String codeBefore, String direction) {//заполнить кодировочную таблицу
        if (node.isLeaf()) {
            encodingArray[(int)node.getLetter()] = codeBefore + direction;
        } else {
            fillEncodingArray(node.getLeftChild(), codeBefore + direction, "0");
            fillEncodingArray(node.getRightChild(), codeBefore + direction, "1");
        }
    }

    String[] getEncodingArray() {
        return encodingArray;
    }

    public void displayEncodingArray() {//для отладки
        fillEncodingArray(huffmanTree.getRoot(), "", "");

        System.out.println("======================Encoding table====================");
        for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
            if (freqArray[i] != 0) {
                System.out.print((char)i + " ");
                System.out.println(encodingArray[i]);
            }
        }
        System.out.println("========================================================");
    }
    //-----------------------------------------------------
    String getOriginalString() {
        return myString;
    }
}

Класс, содержащий который кодирует/декодирует:

public class HuffmanOperator {
    private final byte ENCODING_TABLE_SIZE = 127;//длина таблицы
    private HuffmanTree mainHuffmanTree;//дерево Хаффмана (используется только для сжатия)
    private String myString;//исходное сообщение
    private int[] freqArray;//частотаная таблица
    private String[] encodingArray;//кодировочная таблица
    private double ratio;//коэффициент сжатия 


    public HuffmanOperator(HuffmanTree MainHuffmanTree) {//for compress
        this.mainHuffmanTree = MainHuffmanTree;

        myString = mainHuffmanTree.getOriginalString();

        encodingArray = mainHuffmanTree.getEncodingArray();

        freqArray = mainHuffmanTree.getFrequenceArray();
    }

    public HuffmanOperator() {}//for extract;

    //---------------------------------------compression-----------------------------------------------------------
    private String getCompressedString() {
        String compressed = "";
        String intermidiate = "";//промежуточная строка(без добавочных нулей)
        //System.out.println("=============================Compression=======================");
        //displayEncodingArray();
        for (int i = 0; i < myString.length(); i++) {
            intermidiate += encodingArray[myString.charAt(i)];
        }
        //Мы не можем писать бит в файл. Поэтому нужно сделать длину сообщения кратной 8=>
        //нужно добавить нули в конец(можно 1, нет разницы)
        byte counter = 0;//количество добавленных в конец нулей (байта в полне хватит: 0<=counter<8<127)
        for (int length = intermidiate.length(), delta = 8 - length % 8; 
        		counter < delta ; counter++) {//delta - количество добавленных нулей
            intermidiate += "0";
        }
        
        //склеить кол-во добавочных нулей в бинарном предаствлении и промежуточную строку 
        compressed = String.format("%8s", Integer.toBinaryString(counter & 0xff)).replace(" ", "0") + intermidiate;
        		
        //идеализированный коэффициент
        setCompressionRatio();
        //System.out.println("===============================================================");
        return compressed;
    }
    
    private void setCompressionRatio() {//посчитать идеализированный коэффициент 
        double sumA = 0, sumB = 0;//A-the original sum
        for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
            if (freqArray[i] != 0) {
                sumA += 8 * freqArray[i];
                sumB += encodingArray[i].length() * freqArray[i];
            }
        }
        ratio = sumA / sumB;
    }

    public byte[] getBytedMsg() {//final compression
        StringBuilder compressedString = new StringBuilder(getCompressedString());
        byte[] compressedBytes = new byte[compressedString.length() / 8];
        for (int i = 0; i < compressedBytes.length; i++) {
                compressedBytes[i] = (byte) Integer.parseInt(compressedString.substring(i * 8, (i + 1) * 8), 2);
        }
        return compressedBytes;
    }
    //---------------------------------------end of compression----------------------------------------------------------------
    //------------------------------------------------------------extract-----------------------------------------------------
    public String extract(String compressed, String[] newEncodingArray) {
        String decompressed = "";
        String current = "";
        String delta = "";
        encodingArray = newEncodingArray;
        
        //displayEncodingArray();
        //получить кол-во вставленных нулей
        for (int i = 0; i < 8; i++) 
        	delta += compressed.charAt(i);
        int ADDED_ZEROES = Integer.parseInt(delta, 2);
       
        for (int i = 8, l = compressed.length() - ADDED_ZEROES; i < l; i++) {
            //i = 8, т.к. первым байтом у нас идет кол-во вставленных нулей
            current += compressed.charAt(i);
            for (int j = 0; j < ENCODING_TABLE_SIZE; j++) {
                if (current.equals(encodingArray[j])) {//если совпало
                    decompressed += (char)j;//то добавляем элемент
                    current = "";//и обнуляем текущую строку
                }
            }
        }

        return decompressed;
    }

    public String getEncodingTable() {
        String enc = "";
    	for (int i = 0; i < encodingArray.length; i++) {
        	if (freqArray[i] != 0) 
        		enc += (char)i + encodingArray[i] + '\n';
        }
    	return enc;
    }

    public double getCompressionRatio() {
        return ratio;
    }


    public void displayEncodingArray() {//для отладки
        System.out.println("======================Encoding table====================");
        for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
            //if (freqArray[i] != 0) {
                System.out.print((char)i + " ");
                System.out.println(encodingArray[i]);
            //}
        }
        System.out.println("========================================================");
    }
    }

Класс, облегчающий запись в файл:

import java.io.File;
import java.io.PrintWriter;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
import java.io.IOException;
import java.io.Closeable;

public class FileOutputHelper implements Closeable {
    private File outputFile;
    private FileOutputStream fileOutputStream;

    public FileOutputHelper(File file) throws FileNotFoundException {
        outputFile = file;
        fileOutputStream = new FileOutputStream(outputFile);
    }

    public void writeByte(byte msg) throws IOException {
        fileOutputStream.write(msg);
    }

    public void writeBytes(byte[] msg) throws IOException {
        fileOutputStream.write(msg);
    }

    public void writeString(String msg) {
    	try (PrintWriter pw = new PrintWriter(outputFile)) {
    		pw.write(msg);
    	} catch (FileNotFoundException e) {
    		System.out.println("Неверный путь, или такого файла не существует!");
    	}
    }

    @Override
    public void close() throws IOException {
        fileOutputStream.close();
    }

    public void finalize() throws IOException {
        close();
    }
}

Класс, облегчающий чтение из файла:

import java.io.FileInputStream;
import java.io.EOFException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.Closeable;
import java.io.File;
import java.io.IOException;

public class FileInputHelper implements Closeable {
	private FileInputStream fileInputStream;
	private BufferedReader fileBufferedReader;
	
	public FileInputHelper(File file) throws IOException {
		fileInputStream = new FileInputStream(file);
		fileBufferedReader = new BufferedReader(new InputStreamReader(fileInputStream));
	}
	
	
    public byte readByte() throws IOException {
    	int cur = fileInputStream.read();
    	if (cur == -1)//если закончился файл
    		throw new EOFException();
    	return (byte)cur;
    }
    
    public String readLine() throws IOException {
    	return fileBufferedReader.readLine();
    }
    
    @Override
    public void close() throws IOException{
    	fileInputStream.close();
    }
}

Ну, и главный класс:

import java.io.File;
import java.nio.charset.MalformedInputException;
import java.io.FileNotFoundException;
import java.io.IOException;
import java.nio.file.Files;
import java.nio.file.NoSuchFileException;
import java.nio.file.Paths;
import java.util.List;
import java.io.EOFException;
public class Main {
	private static final byte ENCODING_TABLE_SIZE = 127;
	
    public static void main(String[] args) throws IOException {
        try {//указываем инструкцию с помощью аргументов командной строки
            if (args[0].equals("--compress") || args[0].equals("-c"))
                compress(args[1]);
            else if ((args[0].equals("--extract") || args[0].equals("-x"))
            		&& (args[2].equals("--table") || args[2].equals("-t"))) {
            	extract(args[1], args[3]);
            }
            else
                throw new IllegalArgumentException();
        } catch (ArrayIndexOutOfBoundsException | IllegalArgumentException e) {
            System.out.println("Неверный формат ввода аргументов ");
            System.out.println("Читайте Readme.txt");
            e.printStackTrace();
        }
    }

	public static void compress(String stringPath) throws IOException {
        List<String> stringList;
        File inputFile = new File(stringPath);
        String s = "";
        File compressedFile, table;
        
        try {
            stringList = Files.readAllLines(Paths.get(inputFile.getAbsolutePath()));
        } catch (NoSuchFileException e) {
            System.out.println("Неверный путь, или такого файла не существует!");
            return;
        } catch (MalformedInputException e) {
        	System.out.println("Текущая кодировка файла не поддерживается");
        	return;
        }

        for (String item : stringList) {
            s += item;
            s += '\n';
        }

        HuffmanOperator operator = new HuffmanOperator(new HuffmanTree(s));

        compressedFile = new File(inputFile.getAbsolutePath() + ".cpr");
        compressedFile.createNewFile();
        try (FileOutputHelper fo = new FileOutputHelper(compressedFile)) {
        	fo.writeBytes(operator.getBytedMsg());
        }
        //create file with encoding table:
        
        table = new File(inputFile.getAbsolutePath() + ".table.txt");
        table.createNewFile();
        try (FileOutputHelper fo = new FileOutputHelper(table)) {
        	fo.writeString(operator.getEncodingTable());
        }
        
        System.out.println("Путь к сжатому файлу: " + compressedFile.getAbsolutePath());
        System.out.println("Путь к кодировочной таблице " + table.getAbsolutePath());
        System.out.println("Без таблицы файл будет невозможно извлечь!");
        
        double idealRatio = Math.round(operator.getCompressionRatio() * 100) / (double) 100;//идеализированный коэффициент
        double realRatio = Math.round((double) inputFile.length() 
        		/ ((double) compressedFile.length() + (double) table.length()) * 100) / (double)100;//настоящий коэффициент
        
        System.out.println("Идеализированный коэффициент сжатия равен " + idealRatio);
        System.out.println("Коэффициент сжатия с учетом кодировочной таблицы " + realRatio);
    }

    public static void extract(String filePath, String tablePath) throws FileNotFoundException, IOException {
        HuffmanOperator operator = new HuffmanOperator();
        File compressedFile = new File(filePath),
        	 tableFile = new File(tablePath),
        	 extractedFile = new File(filePath + ".xtr");
        String compressed = "";
        String[] encodingArray = new String[ENCODING_TABLE_SIZE];
        //read compressed file
        //!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!check here:
        try (FileInputHelper fi = new FileInputHelper(compressedFile)) {
        	byte b;
        	while (true) {
        		b = fi.readByte();//method returns EOFException
        		compressed += String.format("%8s", Integer.toBinaryString(b & 0xff)).replace(" ", "0");
        	}
        } catch (EOFException e) {
        	
        }
        
        //--------------------
        
        //read encoding table:
        try (FileInputHelper fi = new FileInputHelper(tableFile)) {
        	fi.readLine();//skip first empty string
        	encodingArray[(byte)'\n'] = fi.readLine();//read code for '\n'
        	while (true) {
        		String s = fi.readLine();
        		if (s == null)
        			throw new EOFException();
        		encodingArray[(byte)s.charAt(0)] = s.substring(1, s.length());        		
        	}
        } catch (EOFException ignore) {}
        
        extractedFile.createNewFile();
        //extract:
		try (FileOutputHelper fo = new FileOutputHelper(extractedFile)) {
			fo.writeString(operator.extract(compressed, encodingArray));
		}
		
		System.out.println("Путь к распакованному файлу " + extractedFile.getAbsolutePath());
    }
}

Файл с инструкциями readme.txt предстоит вам написать самим :-)

Заключение

Наверное, это все что я хотел сказать. Если у вас есть что сказать по поводу моей некомпетентности улучшений в коде, алгоритме, вообще любой оптимизации, то смело пишите. Если я что-то недообъяснил, тоже пишите. Буду рад услышать вас в комментариях!

P.S.

Да-да, я все еще здесь, ведь я не забыл про коэффициент. Для строки s1 кодировочная таблица весит 48 байт — намного больше исходного файла, да и про добавочные нули не забыли(количество добавленных нулей равно 7)=> коэффициент сжатия будет меньше единицы: 176/(65 + 48*8 + 7)=0.38. Если вы тоже это заметили, то только не по лицу вы молодец. Да, эта реализация будет крайне неэффективной для малых файлов. Но что же происходит с большими файлами? Размеры файла намного превышают размер кодировочной таблицы. Вот здесь-то алгоритм работает как-надо! Например, для монолога Фауста архиватор выдает реальный (не идеализированный) коэффициент, равный 1.46 — почти в полтора раза! И да, предполагалось, что файл будет на английском языке.