С момента выхода в августе 2018, язык Julia активно набирает популярность, войдя в топ 10 языков на Github и топ 20 самых популярных профессиональных навыков по версии Upwork. Для начинающих стартуют курсы и выпускаются книги. Julia используется для планирования космических миссий, фармакометрики и климатического моделирования.

Перед тем как приступить к распределенным вычислениям в Julia обратимся к опыту тех, кто уже испробовал данную возможность нового ЯП для прикладных задач — от уравнения диффузии на двух ядрах, до астрономических карт на суперкомпьютере.

Параллельные вычисления и факторы, влияющие на производительность параллельных вычислений

Большинство современных компьютеров имеют более одного процессора, а несколько компьютеров можно объединить в кластер. Использование мощности нескольких процессоров позволяет быстрее выполнять многие вычисления. На производительность влияют два основных фактора: скорость самих процессоров и скорость их доступа к памяти. В кластере данный ЦП будет иметь самый быстрый доступ к ОЗУ расположенной на том же компьютере или узле. Еще более удивительно, что подобные проблемы актуальны на типичном многоядерном ноутбуке из-за различий в скорости основной памяти и кеша. Следовательно, хорошая многопроцессорная среда должна позволять контролировать использование части памяти конкретным процессором.

Параллельные вычисления в Julia

У Джулии есть несколько встроенных примитивов для параллельных вычислений на каждом уровне: векторизация (SIMD), многопоточность и распределенные вычисления.

Собственная многопоточность Джулии позволяет пользователю использовать возможности многоядерного ноутбука, в то время как примитивы удаленного вызова и удаленной выборки позволяют распределять работу по многим процессам в кластере. В дополнение к этим встроенным примитивам ряд пакетов в экосистеме Julia обеспечивает эффективную параллельную обработку.

Автоматическая векторизация в Julia

Современные чипы Intel предоставляют ряд расширений наборов команд. Среди них — различные версии Streaming SIMD Extension (SSE) и несколько поколений векторных расширений (доступны в последних семействах процессоров). Эти расширения обеспечивают программирование в стиле Single Instruction Multiple Data (SIMD), обеспечивая значительное ускорение для кода, поддающегося такому стилю программирования. Мощный компилятор Julia на основе LLVM может автоматически генерировать высокоэффективный машинный код для базовых и пользовательских функций на любой архитектуре, такой как SIMD Hardware (поддерживаемая LLVM), что позволяет пользователю меньше беспокоиться о написании специализированного кода для каждой из этих архитектур. Еще одно преимущество использования компилятора для повышения производительности, а не для ручного кодирования «горячих циклов» в сборке, заключается в том, что это значительно лучше для будущего. Всякий раз, когда выходит архитектура набора команд следующего поколения, пользовательский код Julia автоматически становится быстрее.

Многопоточность

Многопоточность у Юлии обычно принимает форму параллельных циклов. Существуют также примитивы для блокировок и атомиков, которые позволяют пользователям синхронизировать свой код. Параллельные примитивы Джулии просты, но мощны. Показано, что они масштабируются до тысяч узлов и обрабатывают терабайты данных.

Распределенные вычисления

Несмотря на то, что встроенных примитивов Julia достаточно для крупномасштабных параллельных развертываний, существует ряд пакетов для более специализированной работы. ClusterManagers.jl предоставляет интерфейсы для ряда систем очередей заданий, обычно используемых в вычислительных кластерах, таких как Sun Grid Engine и Slurm. DistributedArrays.jl предоставляет удобный интерфейс для массивов данных, распределенных по кластеру. Это объединяет ресурсы памяти нескольких машин, что позволяет использовать массивы, слишком большие для размещения на одной машине. Каждый процесс работает на той части массива, которой он владеет, предоставляя готовый ответ на вопрос о том, как программа должна быть разделена между машинами.

В некоторых унаследованных приложениях пользователи предпочитают не переосмысливать свою параллельную модель и хотят продолжать использовать параллелизм в стиле MPI. Для них MPI.jl предоставляет тонкую оболочку вокруг MPI, которая позволяет пользователям использовать процедуры передачи сообщений в стиле MPI.

Julia в боевых условиях

The Celeste Project — это сотрудничество Julia Computing, Intel Labs, JuliaLabs@MIT, Lawrence Berkeley National Labs и Калифорнийского университета в Беркли.

Celeste — это полностью генеративная иерархическая модель, которая использует статистический вывод для математического определения местоположения и характеристики источников света в небе. Эта модель позволяет астрономам определять перспективные галактики для нацеливания спектрографов и помогает понять роль темной энергии, темной материи и геометрию вселенной.

Пример из Sloan Digital Sky Survey (SDSS)

Используя собственные возможности параллельных вычислений Джулии, исследовательская группа Celeste обработала 55 терабайт визуальных данных и классифицировала 188 миллионов астрономических объектов всего за 15 минут, в результате чего был получен первый полный каталог всех видимых объектов из Sloan Digital Sky Survey. Это одна из крупнейших задач математической оптимизации, когда-либо решаемых человечеством.

В проекте Celeste использовалось 9 300 узлов Knights Landing (KNL) на суперкомпьютере NERSC Cori Phase II для выполнения 1,3 миллиона потоков на ядрах 650 000 KNL, что позволило объединить список приложений с быстродействием, превышающим 1 петафлоп в секунду, что делает Julia единственным динамичным языком высокого уровня, который когда-либо достиг такого подвига. ?? А синхронизация телескопов и обработка данных для снимка черной дыры 10.04.19 побила ли этот рекорд? Вроде как там по-большей части использовался Python

Параллельное программирование с Julia с использованием MPI

Перевод материала из блога Claudio занимающегося физикой плазмы 2018-09-30

Julia существует с 2012 года, и после более чем шести лет разработки, версия 1.0 была наконец выпущена. Это важный этап, который вдохновил меня на создание нового поста (после нескольких месяцев молчания). На этот раз мы увидим, как выполнять параллельное программирование в Julia с использованием парадигмы интерфейса передачи сообщений (MPI) через библиотеку с открытым исходным кодом Open MPI. Мы сделаем это, решив реальную физическую задачу: диффузию тепла через двумерную область.

Рисунок 1. Суперкомпьютер Sequoia в LLNL с почти 1,6 миллионами процессоров, доступных для численного моделирования ядерного оружия. hpc.llnl.gov

Это будет довольно продвинутое приложение MPI, нацеленное на тех, кто уже имеет некоторое представление о параллельных вычислениях. Из-за этого я не собираюсь идти шаг за шагом, а скорее сосредоточусь на конкретных аспектах, которые, по моему мнению, представляют интерес (в частности, использование ячеек-призраков и передача сообщений в двумерной сетке). Следуя традиции своих недавних постов, обсуждаемый здесь код будет выкладываться лишь частично. Это сопровождается полнофункциональным решением, которое вы можете найти на Github — Diffusion.jl.

Параллельные вычисления вошли в «коммерческий мир» за последние несколько лет. Это стандартное решение для приложений ETL (Extract-Transform-Load), где рассматриваемая проблема смущающе параллельна: каждый процесс выполняется независимо от всех остальных, и не требуется никакой сетевой связи (пока не произойдет окончательный шаг «сокращения», где каждое локальное решение собрано в глобальное решение).

Во многих научных приложениях необходимо передавать информацию через сеть кластера. Эти «дожути параллельные» проблемы часто представляют собой численное моделирование: задачи астрофизики, моделирование погоды, биология, квантовые системы и т.д. В некоторых случаях эти симуляции выполняются на десятках и даже миллионах процессоров (рис. 1), а память распределяется между различными процессорами. Как правило, эти процессоры взаимодействуют в суперкомпьютере через парадигму интерфейса передачи сообщений (MPI).

Любой, кто работает в высокопроизводительных вычислениях, должен быть знаком с MPI. Он позволяет использовать архитектуру кластера на очень низком уровне. Теоретически, исследователь может назначить каждому ЦП свою вычислительную нагрузку. Он / она может точно решить, когда и какую информацию следует передавать между процессорами, и должно ли это происходить синхронно или асинхронно.

А теперь давайте вернемся к содержанию этого поста, где мы увидим, как написать решение уравнения диффузионного типа с использованием MPI. Мы уже обсуждали явную схему для одномерного уравнения этого типа (Мы, кстати, тоже такое обсуждали). Однако в этом посте мы рассмотрим двумерное решение.

Код Julia, представленный здесь, по сути является переводом кода C / Fortran, объясненного в том великолепном посте Фабьена Дурнака.

В этом посте я не буду подробно анализировать скорость масштабирования и количество процессоров. Главным образом потому, что у меня есть только два процессора, с которыми я могу играть дома (процессор Intel Core i7 на моем MacBook Pro)… Тем не менее, я все еще могу с гордостью сказать, что код Julia, представленный в этом посте, показывает значительное ускорение при использовании двух процессоров против одного. Да и вообще: она быстрее, чем эквивалентные коды Fortran и C! (подробнее об этом позже)

Вот темы, которые мы собираемся затронуть в этом посте:

• Юлия: Мои первые впечатления
• Как установить Open MPI на вашем компьютере
• Проблема: распространение через двумерный домен
• Связь между процессорами: потребность в призрачных ячейках
• Использование MPI
• Визуализация решения
• Производительность
• Выводы

1. Первые впечатления о Julia

На самом деле, я с Юлией познакомился недавно, поэтому решил здесь заостриться на паре «первых впечатлений».

Основная причина, по которой я заинтересовался Джулией, заключается в том, что она обещает быть фреймворком общего назначения с производительностью, сравнимой с C и Fortran, сохраняя при этом гибкость и простоту использования таких языков сценариев, как Matlab или Python. По сути, в Джулии должна быть возможность писать приложения Data Science / High-Performance-Computing, которые работают на локальном компьютере, в облаке или на корпоративных суперкомпьютерах.

Один аспект, который мне не нравится, — это рабочий процесс, который кажется неоптимальным для тех, кто, как я, ежедневно использует IntelliJ и PyCharm (плагин IntelliJ Julia ужасен). Я также попробовал Juno IDE, это, пожалуй, лучшее решение на данный момент, но мне все еще нужно привыкнуть к нему.

Одним из аспектов, демонстрирующих, как Юлия еще не достигла своей «зрелости», является то, насколько разнообразной и устаревшей является документация многих пакетов (для пакетов держащихся на плаву всё уже перелопатили с прошлого года). Я до сих пор не нашел способа записать матрицу чисел с плавающей точкой на диск в отформатированном виде (теперь уже найти легко). Конечно, вы можете записать на диск каждый элемент матрицы в цикле double-for, но должны быть доступны лучшие решения. Просто эту информацию трудно найти, а документация обязана быть исчерпывающей.

Другим аспектом, который выделяется при первом использовании Julia, является выбор использования индексации с единицы для массивов. Хотя я нахожу это немного раздражающим с практической точки зрения, это, конечно, не нарушает договоренности, учитывая, что это не уникально для Джулии (Matlab и Fortran также используют индексацию начинающуюся с одного).

Теперь, к хорошему и самому важному аспекту: Джулия действительно может быть очень быстрой. Я был впечатлен, увидев, как код Julia, который я написал для этого поста, может работать лучше, чем эквивалентный код на Fortran и C, несмотря на то, что по сути только что перевел его на Julia. Посмотрите на раздел производительности, если вам интересно.

2. Установка Open MPI

Open MPI — это библиотека интерфейса передачи сообщений с открытым исходным кодом. Другие известные библиотеки включают MPICH и MVAPICH. MVAPICH, разработанный Университетом штата Огайо, на данный момент является самой продвинутой библиотекой, поскольку она также может поддерживать кластеры графических процессоров — что особенно полезно для приложений Deep Learning (действительно, между NVIDIA и командой MVAPICH существует тесное сотрудничество).

Все эти библиотеки построены на общем интерфейсе: MPI API. Поэтому не имеет значения, используете ли вы одну или другую библиотеку: написанный вами код может остаться прежним.

Проект MPI.jl на Github — это оболочка для MPI. Под капотом он использует C и Fortran установки MPI. Он отлично работает, хотя ему не хватает некоторых функций, доступных на этих других языках.

Чтобы запустить MPI в Julia, вам нужно будет установить отдельно Open MPI на ваш компьютер. Если у вас есть Mac, я нашел это руководство очень полезным. Важно отметить, что вам также потребуется установить gcc (компилятор GNU), поскольку для Open MPI требуются компиляторы Fortran и C. Я установил версию Open MPI 3.1.1, что также подтверждается mpiexec --version на моем терминале.

После того, как на вашем компьютере установлен Open MPI, вы должны установить cmake. Опять же, если у вас Mac, это так же просто, как набрать brew install cmake на вашем терминале.

На данный момент вы готовы установить пакет MPI в Julia. Откройте Julia REPL и введите using Pkg Pkg.add («MPI»). Обычно в этот момент вы должны иметь возможность импортировать пакет, используя MPI для импорта. Однако мне также пришлось собрать пакет через Pkg.build («MPI»), прежде чем все заработало.

3. Задача: двумерное уравнение диффузии

Уравнение диффузии является примером параболического уравнения в частных производных. Он описывает такие явления, как диффузия тепла или диффузия концентрации (второй закон Фика). В двух пространственных измерениях уравнение диффузии записывается

Решение $$ показывает, как изменяется температура / концентрация (в зависимости от того, изучаем ли мы распространение тепла или диффузию веществ) в пространстве и времени. Действительно, переменные x и y представляют пространственные координаты, а временная компонента представлена переменной t. Величина D является «коэффициентом диффузии» и определяет, как быстро, например, тепло будет распространяться через физическую область. Аналогично тому, что обсуждалось (более подробно) в предыдущем посте блога, приведенное выше уравнение может быть дискретизировано с использованием так называемой «явной схемы» решения. Я не буду вдаваться в подробности, которые вы можете найти в блоге, достаточно записать числовое решение в следующей форме:

где i и k индексы пробегающие по пространственной сетке, j по времени. Первый временной слой заполняется из начальных условий, а каждый последующий $$ вычисляется с использованием значений предыдущего слоя. На рисунке красными кружочками обозначены узлы слоя $$, которые нужны для вычисления значения в точке $$

Уравнение (1) действительно все, что нужно для того, чтобы найти решение по всей области на каждом последующем временном шаге. Довольно просто реализовать код, который делает это последовательно, с одним процессом на CPU. Однако здесь мы хотим обсудить параллельную реализацию, которая использует несколько процессов.

Каждый процесс будет отвечать за поиск решения в части всей пространственной области. Такие проблемы, как диффузия тепла, которые не являются явнымии претендентами на распределенные вычисления, требуют обмена информацией между процессами. Чтобы прояснить этот момент, давайте посмотрим на рисунок

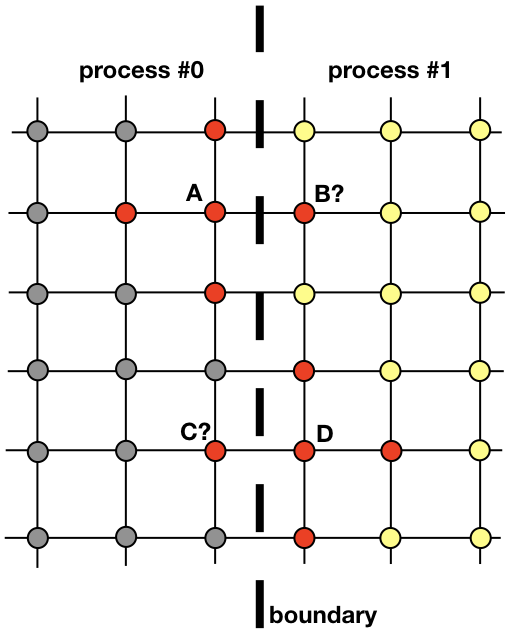
Два соседних процесса должны взаимодействовать, чтобы найти решение вблизи границы. Процесс 0 должен знать значение решения в B, чтобы рассчитать решение в точке сетки A. Аналогично, процесс 1 должен знать значение в точке C, чтобы вычислить решение в точке сетки D. Эти значения неизвестны процессам, пока не произойдет связь между процессами 0 и 1.

Он показывает, как процессы 0 и 1 должны будут взаимодействовать, чтобы оценить решение вблизи границы. Тут-то на сцену и выходит MPI. В следующем разделе мы рассмотрим эффективный способ обмена сообщениями.

4. Связь между процессами: призрачные ячейки

Важным понятием в вычислительной гидродинамике является понятие призрачных ячеек. Эта концепция полезна всякий раз, когда пространственный домен разлагается на несколько поддоменов, каждый из которых решается одним процессом.

Чтобы понять, что такое призрачные ячейки, давайте снова рассмотрим две соседние области на предыдущем изображении. Процесс 0 отвечает за поиск решения с левой стороны, тогда как процесс 1 находит его с правой стороны пространственного домена. Однако из-за формы трафарета (рис. 2) вблизи границы оба процесса должны будут обмениваться данными между собой. Вот проблема: очень неэффективно, чтобы процесс 0 и процесс 1 связывались каждый раз, когда им нужен узел из соседнего процесса: это привело бы к неприемлемым издержкам связи.

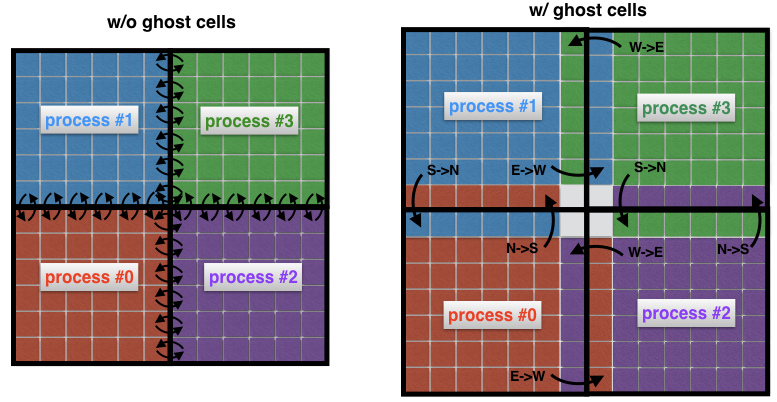
Рис.4 Связь между процессами без (слева) и с (справа) призрачными клетками. Без промежуточных ячеек каждая ячейка на границе субдомена должна передавать свое собственное сообщение соседнему процессу. Использование ячеек-призраков позволяет минимизировать количество передаваемых сообщений, так как многие ячейки, принадлежащие границам процесса, обмениваются одновременно одним сообщением. Здесь, например, процесс 0 передает всю северную границу процессу 1, а всю восточную границу процессу 2.

Вместо этого, обычной практикой является окружение «настоящих» поддоменов дополнительными ячейками, называемыми ячейками-призраками, как показано на рисунке 4 (справа). Эти клетки-призраки представляют собой копии решения на границах соседних поддоменов. На каждом временном шаге старая граница каждого субдомена передается соседям. Это позволяет рассчитывать новое решение на границе субдомена со значительно сниженными накладными расходами на связь. Чистый эффект — ускорение в коде.

5. Использование MPI

Существует множество учебных пособий по MPI. Здесь я просто хочу описать те команды, выраженные на языке оболочки MPI.jl для Джулии, которые я использовал для решения проблемы двумерной диффузии. Это некоторые основные команды, которые используются практически в каждой реализации MPI.

5.1 Нахождение соседей процесса

Для нашей задачи мы собираемся разложить нашу двумерную область на множество прямоугольных субдоменов, как показано на рисунке ниже.

Рисунок 5. Декартовое разложение двумерной области, разделенной на 12 субдоменов. Обратите внимание, что ранги MPI (идентификаторы процессов) начинаются с нуля.

Обратите внимание, что оси x и y перевернуты относительно обычного использования, чтобы связать ось x со строками и ось y со столбцами матрицы решения.

Чтобы общаться между различными процессами, каждый процесс должен знать своих соседей. Существует очень удобная команда MPI, которая делает это автоматически и называется MPI_Cart_create. К сожалению, оболочка Julia MPI не включает эту продвинутую команду (и ее добавление не кажется тривиальной), поэтому вместо этого я решил создать функцию, которая выполняет ту же задачу. Чтобы сделать её более компактной, я часто использовал тернарный оператор. Вы можете найти эту функцию ниже

function neighbors(my_id::Int, nproc::Int, nx_domains::Int, ny_domains::Int)
    id_pos = Array{Int,2}(undef, nx_domains, ny_domains)
    for id = 0:nproc-1
        n_row = (id+1) % nx_domains > 0 ? (id+1) % nx_domains : nx_domains
        n_col = ceil(Int, (id + 1) / nx_domains)
        if (id == my_id)
            global my_row = n_row
            global my_col = n_col
        end
        id_pos[n_row, n_col] = id
    end

    neighbor_N = my_row + 1 <= nx_domains ? my_row + 1 : -1
    neighbor_S = my_row - 1 > 0 ? my_row - 1 : -1
    neighbor_E = my_col + 1 <= ny_domains ? my_col + 1 : -1
    neighbor_W = my_col - 1 > 0 ? my_col - 1 : -1

    neighbors = Dict{String,Int}()
    neighbors["N"] = neighbor_N >= 0 ? id_pos[neighbor_N, my_col] : -1
    neighbors["S"] = neighbor_S >= 0 ? id_pos[neighbor_S, my_col] : -1
    neighbors["E"] = neighbor_E >= 0 ? id_pos[my_row, neighbor_E] : -1
    neighbors["W"] = neighbor_W >= 0 ? id_pos[my_row, neighbor_W] : -1

    return neighbors
end

Подобное мы делали когда строили лабиринты

Входными данными этой функции являются my_id, который является рангом (или идентификатором) процесса, число процессов nproc, число делений в направлении x nx_domains и количество делений в направлении y ny_domains.

Давайте сейчас проверим эту функцию. Например, снова глядя на рис. 5, мы можем проверить выходные данные для процесса ранга 4 и процесса ранга 11. Вобьём в REPL:

julia> neighbors(4, 12, 3, 4)

Dict{String,Int64} with 4 entries:
  "S" => 3
  "W" => 1
  "N" => 5
  "E" => 7

и

julia> neighbors(11, 12, 3, 4)
Dict{String,Int64} with 4 entries:
  "S" => 10
  "W" => 8
  "N" => -1
  "E" => -1

Как видите, я использую кардинальные направления "N", "S", "E", "W" для обозначения местоположения соседа. Например, процесс 4 имеет процесс 3 в качестве соседа, расположенного к югу от его позиции. Вы можете проверить, что все вышеприведенные результаты верны, учитывая, что «-1» во втором примере означает, что не было найдено соседей на "северной" и "восточной" сторонах процесса 11.

5.2 Передача сообщений

Как мы видели ранее, на каждой итерации каждый процесс отправляет свои границы соседним процессам. В то же время каждый процесс получает данные от своих соседей. Эти данные хранятся каждым процессом в виде "призрачных ячеек" и используются для вычисления решения вблизи границы каждого субдомена.

В MPI есть очень полезная команда MPI_Sendrecv, которая позволяет отправлять и получать сообщения одновременно между двумя процессами. К сожалению, MPI.jl не обеспечивает эту функциональность, однако все еще возможно достичь того же результата, используя функции MPI_Send и MPI_Receive отдельно.

Вот что сделано в следующей функции updateBound!, которая обновляет ячейки-призраки на каждой итерации. Входными данными этой функции являются глобальное 2D-решение u, которое включает в себя призрачные ячейки, а также всю информацию, относящуюся к конкретному процессу, выполняющему функцию (каков ее ранг, каковы координаты ее субдомена, каковы его соседи). Функция сначала отправляет свои границы соседям, а затем получает их границы. Принимающая часть дорабатывается через команду MPI.Waitall!, которая гарантирует, что все ожидаемые сообщения были получены до обновления побочных ячеек для конкретного поддомена, представляющего интерес.

function updateBound!(u::Array{Float64,2}, size_total_x, size_total_y, neighbors, comm,
                       me, xs, ys, xe, ye, xcell, ycell, nproc)

    mep1 = me + 1

    #assume, to start with, that this process is not going to receive anything
    rreq = Dict{String, MPI.Request}(
                                "N" => MPI.REQUEST_NULL,
                                "S" => MPI.REQUEST_NULL,
                                "E" => MPI.REQUEST_NULL,
                                "W" => MPI.REQUEST_NULL
                                )
    recv = Dict{String, Array{Float64,1}}()
    ghost_boundaries = Dict{String, Any}(
                                "N" => (xe[mep1]+1, ys[mep1]:ye[mep1]),
                                "S" => (xs[mep1]-1, ys[mep1]:ye[mep1]),
                                "E" => (xs[mep1]:xe[mep1], ye[mep1]+1),
                                "W" => (xs[mep1]:xe[mep1], ys[mep1]-1)
                                )
    is_receiving = Dict{String, Bool}("N" => false, "S" => false, "E" => false, "W" => false)

    #send
    neighbors["N"] >=0 && MPI.Isend(u[xe[mep1], ys[mep1]:ye[mep1]], neighbors["N"], me + 40, comm)
    neighbors["S"] >=0 && MPI.Isend(u[xs[mep1], ys[mep1]:ye[mep1]], neighbors["S"], me + 50, comm)
    neighbors["E"] >=0 && MPI.Isend(u[xs[mep1]:xe[mep1], ye[mep1]], neighbors["E"], me + 60, comm)
    neighbors["W"] >=0 && MPI.Isend(u[xs[mep1]:xe[mep1], ys[mep1]], neighbors["W"], me + 70, comm)

    #receive
    if (neighbors["N"] >= 0)
        recv["N"] = Array{Float64,1}(undef, ycell)
        is_receiving["N"] = true
        rreq["N"] = MPI.Irecv!(recv["N"], neighbors["N"], neighbors["N"] + 50, comm)
    end
    if (neighbors["S"] >= 0)
        recv["S"] = Array{Float64,1}(undef, ycell)
        is_receiving["S"] = true
        rreq["S"] = MPI.Irecv!(recv["S"], neighbors["S"], neighbors["S"] + 40, comm)
    end
    if (neighbors["E"] >= 0)
        recv["E"] = Array{Float64,1}(undef, xcell)
        is_receiving["E"] = true
        rreq["E"] = MPI.Irecv!(recv["E"], neighbors["E"], neighbors["E"] + 70, comm)
    end
    if (neighbors["W"] >= 0)
        recv["W"] = Array{Float64,1}(undef, xcell)
        is_receiving["W"] = true
        rreq["W"] = MPI.Irecv!(recv["W"], neighbors["W"], neighbors["W"] + 60, comm)
    end

    MPI.Waitall!([rreq[k] for k in keys(rreq)])
    for (k, v) in is_receiving
        if v
            u[ghost_boundaries[k][1], ghost_boundaries[k][2]] = recv[k]
        end
    end
end

5. Визуализация решения

Домен инициализируется постоянным значением u = +10 вокруг границы, что можно интерпретировать как наличие источника постоянной температуры на границе. Начальное условие u = ?10 внутри области (рис. 6 слева). С течением времени значение u = 10 на границе диффундирует к центру области. Например, на этапе j = 15203 решение выглядит так, как показано на рис. 6 справа.

С увеличением времени t решение становится все более однородным, пока теоретически для $$ оно не станет u = +10 по всему домену.

Рис. 6. Начальное условие (слева) и решение на шаге 15203 по времени (справа). Границы области всегда сохраняются на значении u = +10. С течением времени решение становится все более однородным и имеет тенденцию становиться все ближе и ближе к значению u = +10 по всей области.

6. Производительность

Я был очень впечатлен, когда проверил производительность реализации Julia по сравнению с Fortran и C: я обнаружил, что реализация Julia самая быстрая!

Прежде чем углубляться в сравнение, давайте посмотрим на производительность MPI самого кода Julia. На рисунке 7 показано соотношение времени выполнения при работе с процессами 1 к 2 (ЦП). В идеале вы хотели бы, чтобы это число было близко к 2, т.е. работа с двумя процессорами должна быть в два раза быстрее, чем с одним процессором. Вместо этого наблюдается то, что для небольших размеров задач (сетка из 128x128 ячеек) время компиляции и накладные расходы на коммуникацию оказывают отрицательное влияние на общее время выполнения: ускорение меньше единицы. Преимущество использования нескольких процессов становится очевидным только для более крупных задач.

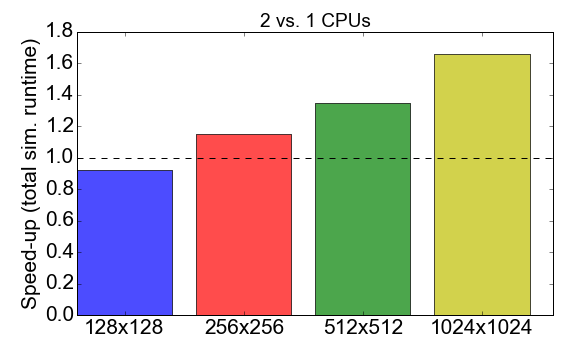
Рисунок 7. Ускорение реализации Julia MPI с двумя процессами против одного процесса в зависимости от сложности задачи (размера сетки). Под «ускорением» подразумевается отношение общего времени выполнения с использованием 1 процесса к 2 процессам.

А теперь неожиданный поворот: на рис. 8 показано, что реализация Julia быстрее, чем Fortran и C, для задач размером 256x256 и 512x512 (только те, которые я тестировал). Здесь я только измеряю время, необходимое для завершения основного цикла итерации. Я считаю, что это справедливое сравнение, поскольку для длительных симуляций это будет самым большим вкладом в общее время выполнения.

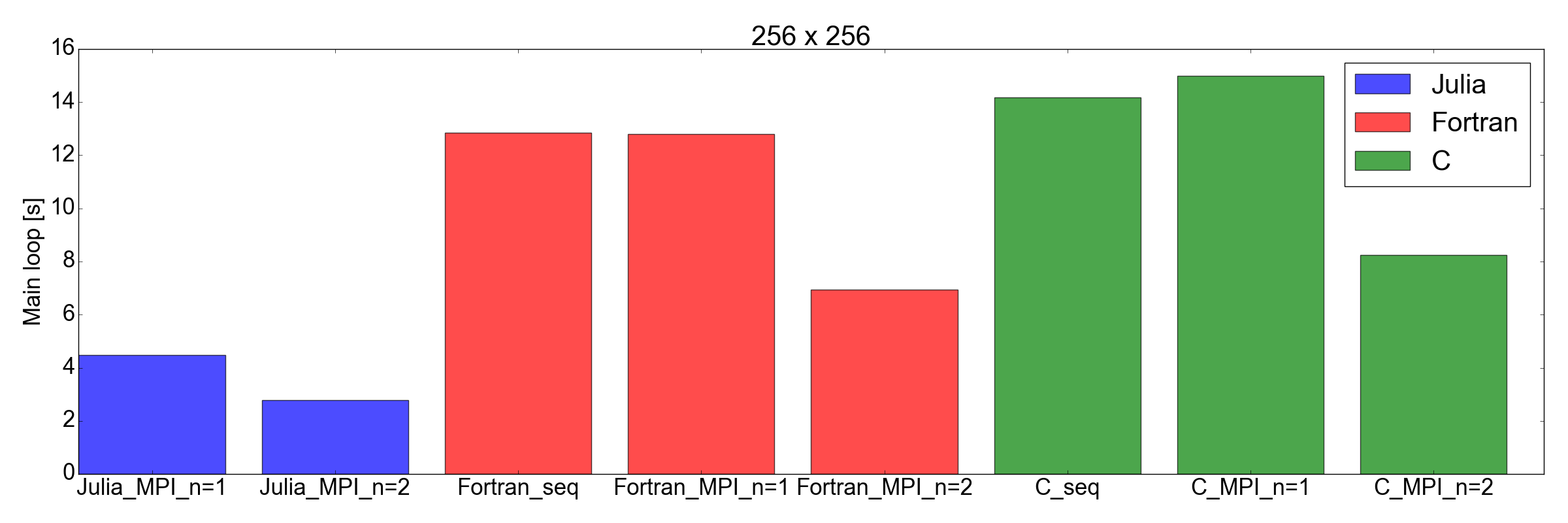
Рисунок 8. Производительность Julia против Fortran против C для двух размеров сетки: 256x256 (вверху) и 512x512 (внизу). Это показывает, что Джулия — лучший исполнительский язык. Производительность измеряется как время, необходимое для выполнения фиксированного числа итераций в основном цикле кода.

Выводы

Прежде чем начать этот пост, я скептически относился к тому, что Джулия может конкурировать со скоростью Фортрана и Си для научных приложений. Основная причина заключалась в том, что я ранее перевел академический код, содержащий около 2000 строк, из Фортрана в Julia 0.6, и я заметил снижение производительности примерно в 3 раза.

Но на этот раз… я очень впечатлен. Я фактически только что перевел существующую реализацию MPI, написанную на Фортране и Си, на Julia 1.0. Результаты, показанные на рис. 8, говорят сами за себя: Юлия, похоже, самая быстрая на сегодняшний день. Обратите внимание, что я не учел длительное время компиляции, потребляемое компилятором Julia, поскольку для «реальных» приложений, для выполнения которых требуются часы, это будет незначительным фактором.

Я также должен добавить, что мои тесты, конечно, не настолько исчерпывающие, как должны быть для тщательного сравнения. На самом деле, мне было бы любопытно посмотреть, как работает код более чем с двумя процессорами (я ограничен моим домашним персональным ноутбуком) и с другим оборудованием (см. Diffusion.jl).

Во всяком случае, это упражнение убедило меня в том, что стоит потратить больше времени на изучение и использование Julia для Data Science и научных приложений. Вперёд, к новым свершениям!

References

• Version MPI du code de resolution numerique de l’equation de chaleur 2D
• Parallel Computing
• Parallel programming with Julia using MPI
• Celeste programm