В данной статье мне хотелось бы изложить реализацию метода конечных элементов на примере уравнения Пуассона. Рассмотрим задачу:

с однородным краевым условием
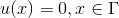
где
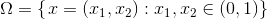


Требуется найти функцию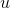 , решающую заданное уравнение.
, решающую заданное уравнение.
Решение
Умножим начальное уравнение на функцию , непрерывную, кусочно непрерывно-дифференцируемую и равную на краях нулю, и проинтегрируем полученное уравнение по всей области
, непрерывную, кусочно непрерывно-дифференцируемую и равную на краях нулю, и проинтегрируем полученное уравнение по всей области 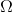 .
.
После применения формулы интегрирования по частям, получим следующее уравнение
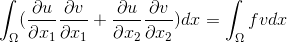
Введем на области квадратную сетку с шагом
квадратную сетку с шагом 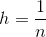 :
:

и каждый квадрат разделим диагональю, параллельной биссектрисе первого координатного угла:
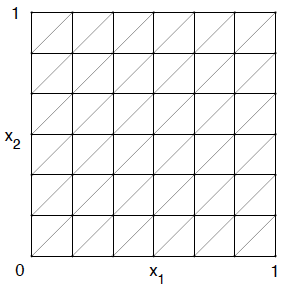
Получим разбиение области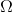 на треугольные элементы
на треугольные элементы 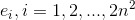 — триангуляция области
— триангуляция области 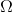 . Триангуляция такого типа называется триангуляцией Фридрихса-Келлера.
. Триангуляция такого типа называется триангуляцией Фридрихса-Келлера.
Будем искать приближенное решение данного уравнения как функцию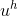 , равную нулю на границе (краевое условие), непрерывную на области
, равную нулю на границе (краевое условие), непрерывную на области 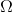 и линейную на каждом полученном элементе триангуляции.
и линейную на каждом полученном элементе триангуляции.
Функцию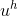 можно представить в следующем виде:
можно представить в следующем виде:
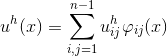
где значения функций в точке определены следующим образом:
определены следующим образом:
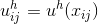

Подставив функцию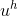 в первое уравнение, осуществив преобразования и вынос констант из под знака интеграла, сведем задачу для каждой базисной функции к подсчету интегралов вида:
в первое уравнение, осуществив преобразования и вынос констант из под знака интеграла, сведем задачу для каждой базисной функции к подсчету интегралов вида:

Значение интеграла может быть не нулевым лишь в том случае, если базисные функции под знаком интеграла имеют непустую общую область определения. По построению, каждый элемент имеет три вершины. Вершина может быть общей максимально для 6 треугольников:
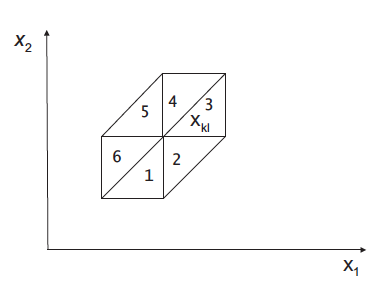
с соответствующими значениями производных для каждого из 6 случаев:

После подсчетов интеграла уравнение с номером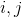 будет выглядеть следующим образом:
будет выглядеть следующим образом:
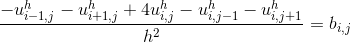
где

и при достаточно малом :
:
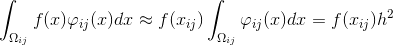
Следовательно, уравнение может быть переписано в следующем виде:
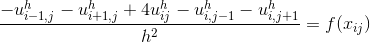
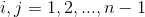
Добавив граничные условия, а именно:
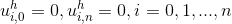

получаем полную СЛАР, решая которую, находим значения функции в точках сетки.
Большое спасибо Р.З. Даутову и М.М. Карчевскому за прекрасную литературу!

с однородным краевым условием
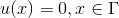
где
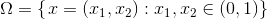


Требуется найти функцию
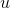 , решающую заданное уравнение.
, решающую заданное уравнение. Решение
Умножим начальное уравнение на функцию
 , непрерывную, кусочно непрерывно-дифференцируемую и равную на краях нулю, и проинтегрируем полученное уравнение по всей области
, непрерывную, кусочно непрерывно-дифференцируемую и равную на краях нулю, и проинтегрируем полученное уравнение по всей области 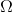 .
. После применения формулы интегрирования по частям, получим следующее уравнение
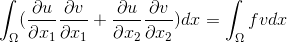
Введем на области
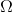 квадратную сетку с шагом
квадратную сетку с шагом 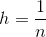 :
:
и каждый квадрат разделим диагональю, параллельной биссектрисе первого координатного угла:

Получим разбиение области
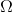 на треугольные элементы
на треугольные элементы 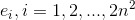 — триангуляция области
— триангуляция области  . Триангуляция такого типа называется триангуляцией Фридрихса-Келлера.
. Триангуляция такого типа называется триангуляцией Фридрихса-Келлера. Будем искать приближенное решение данного уравнения как функцию
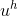 , равную нулю на границе (краевое условие), непрерывную на области
, равную нулю на границе (краевое условие), непрерывную на области  и линейную на каждом полученном элементе триангуляции.
и линейную на каждом полученном элементе триангуляции. Функцию
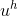 можно представить в следующем виде:
можно представить в следующем виде: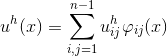
где значения функций в точке
 определены следующим образом:
определены следующим образом: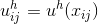

Подставив функцию
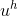 в первое уравнение, осуществив преобразования и вынос констант из под знака интеграла, сведем задачу для каждой базисной функции к подсчету интегралов вида:
в первое уравнение, осуществив преобразования и вынос констант из под знака интеграла, сведем задачу для каждой базисной функции к подсчету интегралов вида: 
Значение интеграла может быть не нулевым лишь в том случае, если базисные функции под знаком интеграла имеют непустую общую область определения. По построению, каждый элемент имеет три вершины. Вершина может быть общей максимально для 6 треугольников:

с соответствующими значениями производных для каждого из 6 случаев:

После подсчетов интеграла уравнение с номером
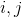 будет выглядеть следующим образом:
будет выглядеть следующим образом: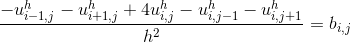
где

и при достаточно малом
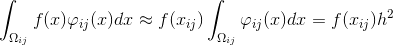
Следовательно, уравнение может быть переписано в следующем виде:
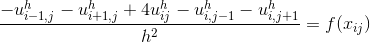
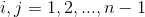
Добавив граничные условия, а именно:
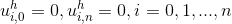

получаем полную СЛАР, решая которую, находим значения функции в точках сетки.
Большое спасибо Р.З. Даутову и М.М. Карчевскому за прекрасную литературу!


maisvendoo
Было бы интересно рассмотреть МКЭ не для уравнения Пуассона, для которого этот метод описывают подавляющее число авторов, а например решение ДУЧП гиперболического типа, описывающие движение воздуха по длинной трубе. Вот таких примеров раз два и обчелся, только в некоторых диссертациях встречал, и то без подробностей реализации конечно-разностной схемы
LetoValery Автор
Конечно, будем работать.