Каждый Android-разработчик использовал RecyclerView для отображения списков и каждый сталкивался с проблемой обновления данных в списке, пока в 2016 году не появился магический класс DiffUtil. Я на пальцах объясню, как на самом деле он работает, и постараюсь рассеять его магию.

Немного истории

Одним из самых распространённых элементов в мобильных приложениях является список, в нашем случае RecyclerView. Это могут быть списки чего угодно: адреса офисов, списки друзей в соц. сетях, история заказов в приложениях такси и т.д. Все эти кейсы объединяет необходимость постоянно менять данные в списке на новые, когда, например, пользователь сделал Swipe to refresh, отфильтровал список или каким-либо другим способом получил пачку новых данных с бека. 

Для реализации такого поведения предок современного Android-разработчика вручную выбирал, какие данные и каким образом изменились, и вызывал соответствующие методы у RecyclerView. Однако всё изменилось, когда Google выпустил Support Library версии 25.1.0, добавив туда DiffUtil, который позволял волшебным образом преобразовывать старый список в новый без полной пересборки RecyclerView. В этой статье я развею волшебство DiffUtil и объясню, как именно он работает.

Как работать с DiffUtil?

Для работы с DiffUtil необходимо реализовать DiffUtil.Callback, вызвать метод calculateDiff(@NonNull Callback cb) и применить к RecyclerView полученный DiffResult методом dispatchUpdatesTo(). Что же происходит при вызове метода calucalteDiff(@NonNull Callback cd)? Данный метод возвращает DiffResult, который содержит набор операций для преобразования изначального списка в новый. Обновления применяются вызовами методов notifyItemRangeInserted, notifyItemRangeRemoved,notifyItemMoved и notifyItemRangeChanged. Первые три метода меняют структуру списка, а именно позиции у элементов, при этом не меняя сами элементы и не вызывая у них onBindViewHolder() (за исключением добавляемого элемента). Последний меняет сам элемент и вызывает onBindViewHolder() для изменения вьюхи элемента.

DiffUtil проверяет два списка на различия, используя алгоритм Майерса, который определяет только наличие/отсутствие изменений, но не умеет находить перемещения элементов. Для этого DiffUtil проходится по созданным алгоритмом Майерса змейкам (об этом дальше), а затем ищет перемещения. DiffResult формируется за 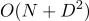если алгоритм не проверяет перемещения элементов и 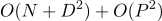, где P – количество добавленных и удалённых элементов. 

Алгоритм Майерса

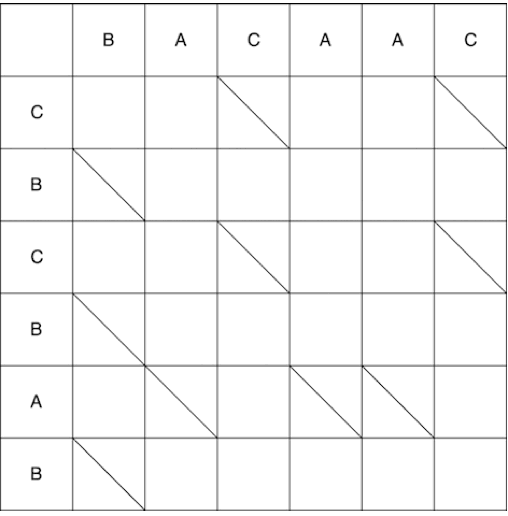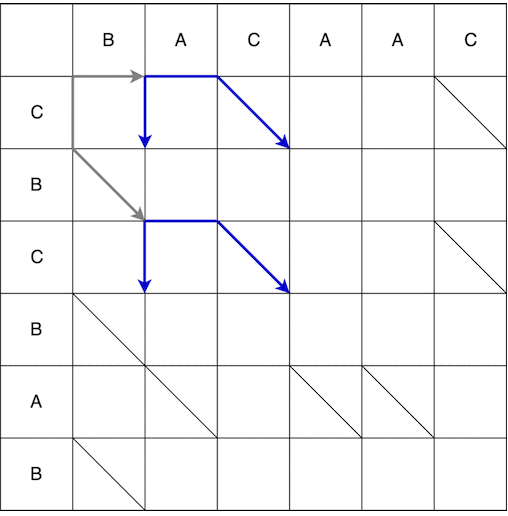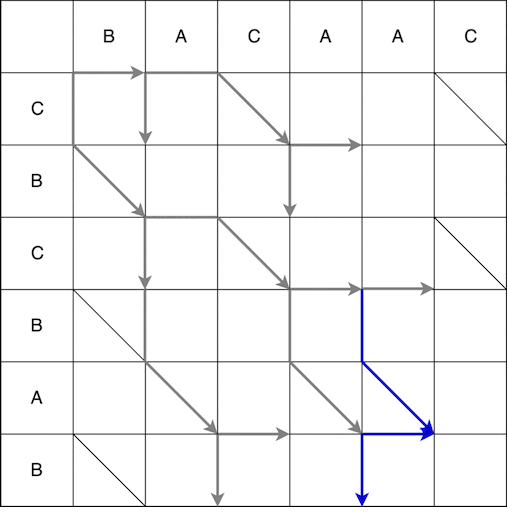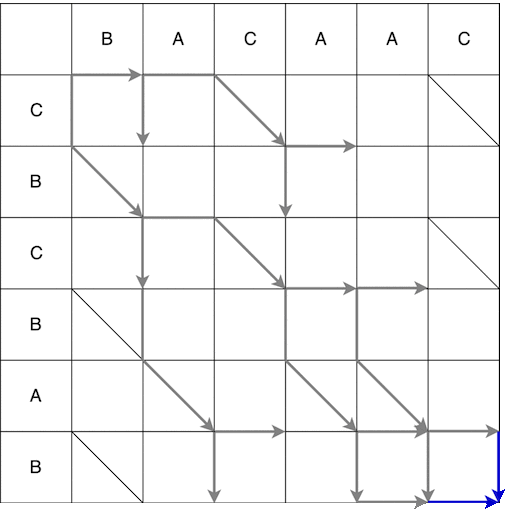
Далее будет рассмотрено объяснение алгоритма Майерса на пальцах, ссылки на математические объяснения алгоритма (а также другие крутые статьи по теме) будут в конце статьи. Рассмотрим две последовательности: BACAAC и CBCBAB. Необходимо написать последовательность преобразований над первой последовательностью, после которых получим вторую. Выпишем последовательности в таблицу следующим образом: старый список будет обозначать первые элементы столбцов, а новый список первые элементы строк.

Перечеркнём ячейки, в которых пересекаются одинаковые элементы обоих последовательностей: 

Дальнейшая задача состоит в том, чтобы дойти из левого верхнего угла матрицы в правый нижний угол за наименьшее количество шагов. Двигаться можно по горизонтальным и вертикальным граням. Если попали в точку, откуда начинается диагональная линия, то обязаны двигаться по ней, однако стоимость такого шага – 0. Соответственно стоимость шага по граням – 1. 

Из точки (0;0) можем двигаться вправо и вниз. При движении вниз необходимо дополнительно пройти по диагонали. Движение, совершаемое за один шаг называется змейкой, в данном случае получили 2 змейки: (0; 0) -> (0; 1) и (0; 0) -> (1; 2). Стрелкой обозначается конец змейки, т.е. если после шага повертикали/горизонтали идёт обязательный шаг по диагонали, то стрелка будет на шаге по диагонали. Ниже показано полное построение змеек из начальной точки в конечную. Некоторые пути на видео были опущены, т.к. были заведомо не самыми короткими.

В итоге получим несколько возможных кратчайших путей, ниже отображены некоторые из них.

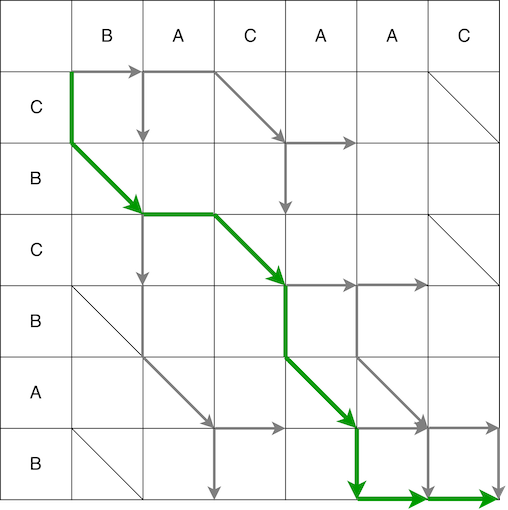
Как прохождение матрицы из крайнего левого угла в крайний правый поможет определить последовательность действий (скрипт) для преобразования одной последовательности в другую? Что значат шаги по горизонтали, вертикали и диагонали? Шаг по матрице в одном из возможных направлений – это действия над старой строкой: 

• Шаг по горизонтали  – удаление из старой строки
• Шаг по вертикали – добавление в старую строку
• Шаг по диагонали – без изменений

На примере второго пути сопоставим путь и получаемый скрипт. Первый шаг – по вертикали, значит добавляем на 0 позицию в старую строку символ «С».

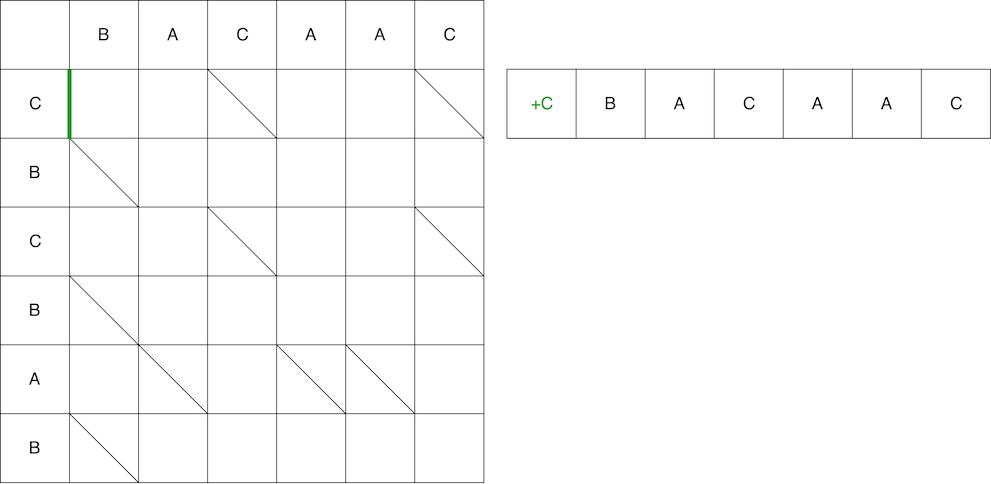
Однако это ещё не вся змейка. Далее мы обязаны двигаться по диагонали. При движении по диагонали элемент B остаётся неизменным. В итоге змейка состоит из движения по вертикали + движение по диагонали.

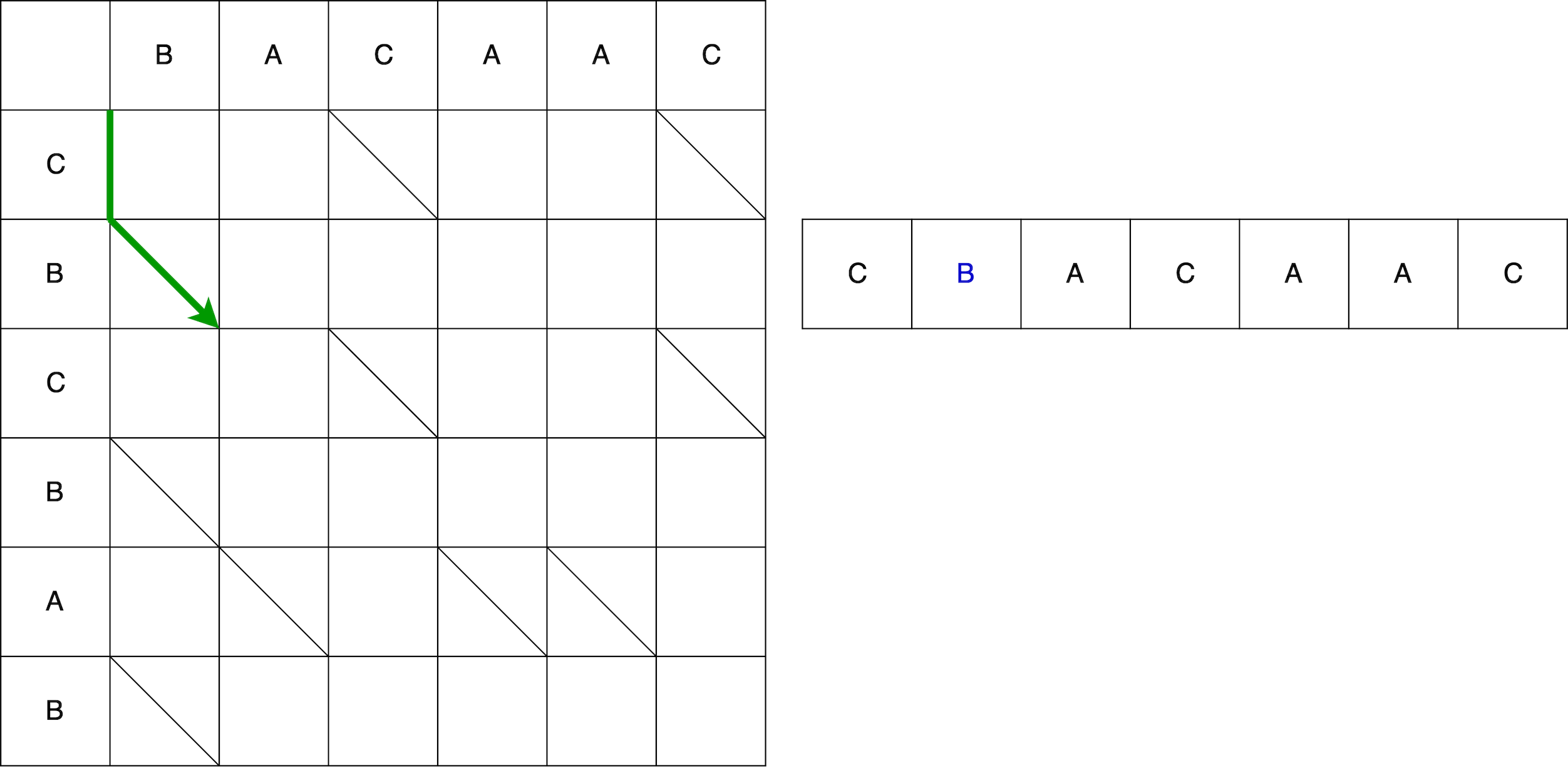
Далее змейка по горизонтали – убираем из старой строки элемент A.

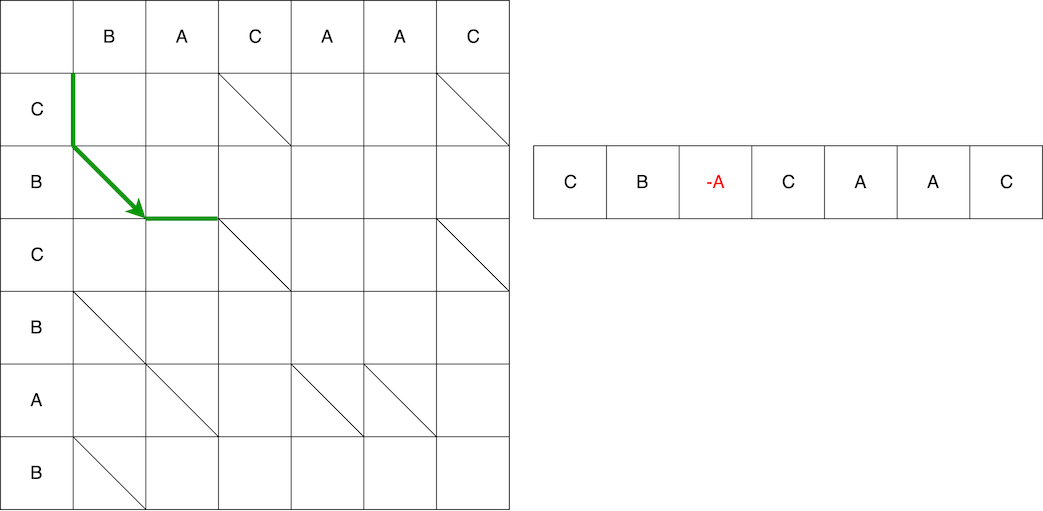
На видео приведён весь путь из начала в конец с изменением исходной строки, пока она не преобразуется в конечную.

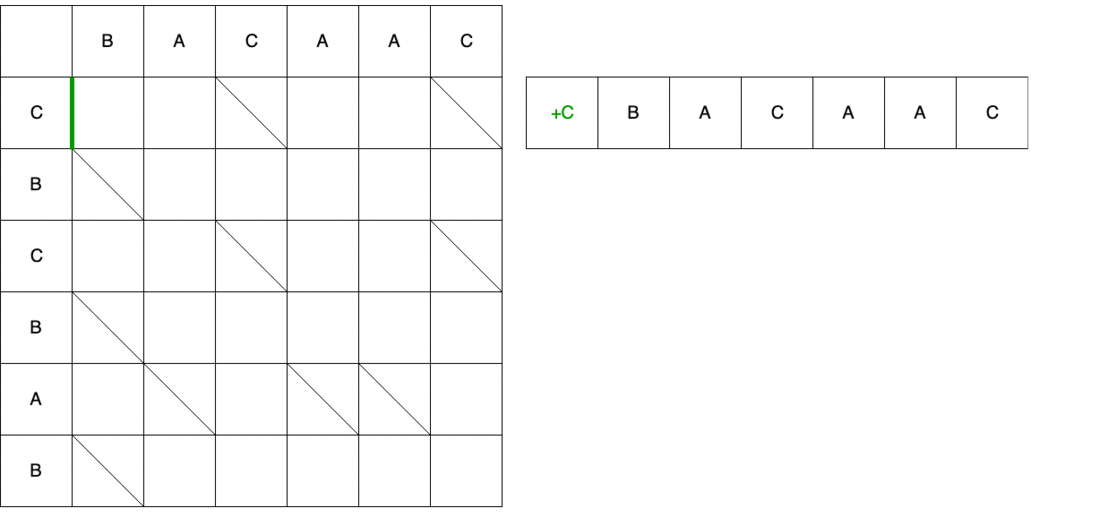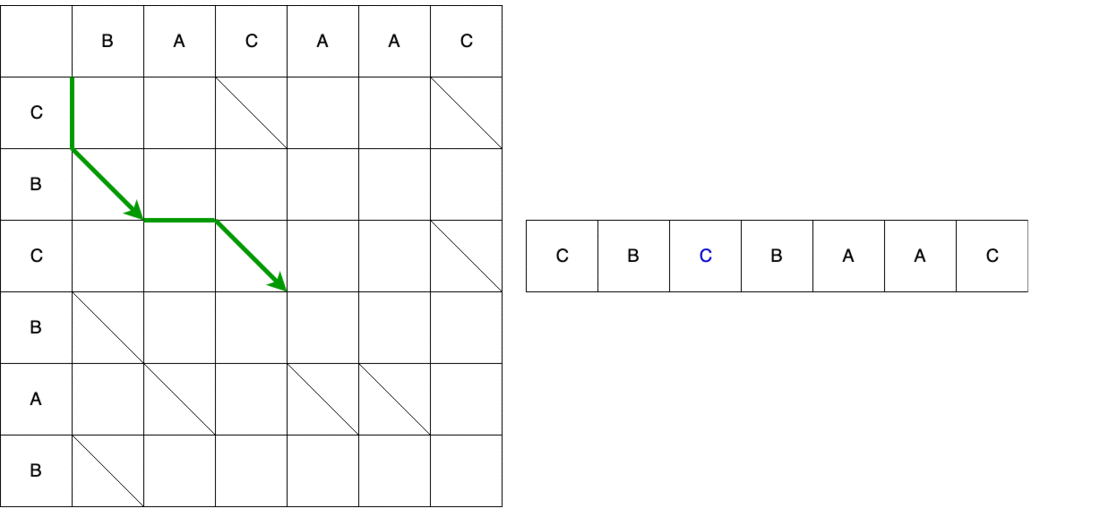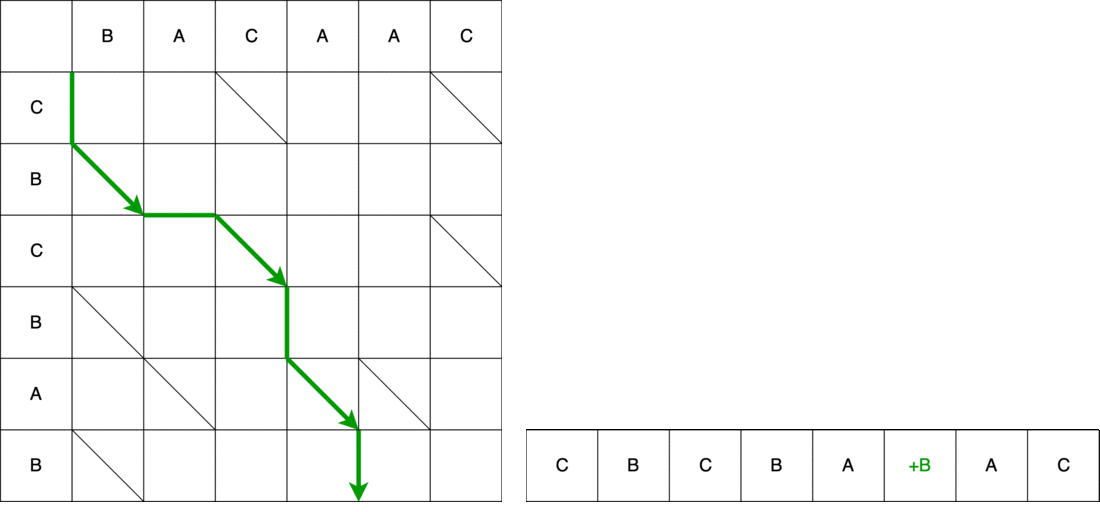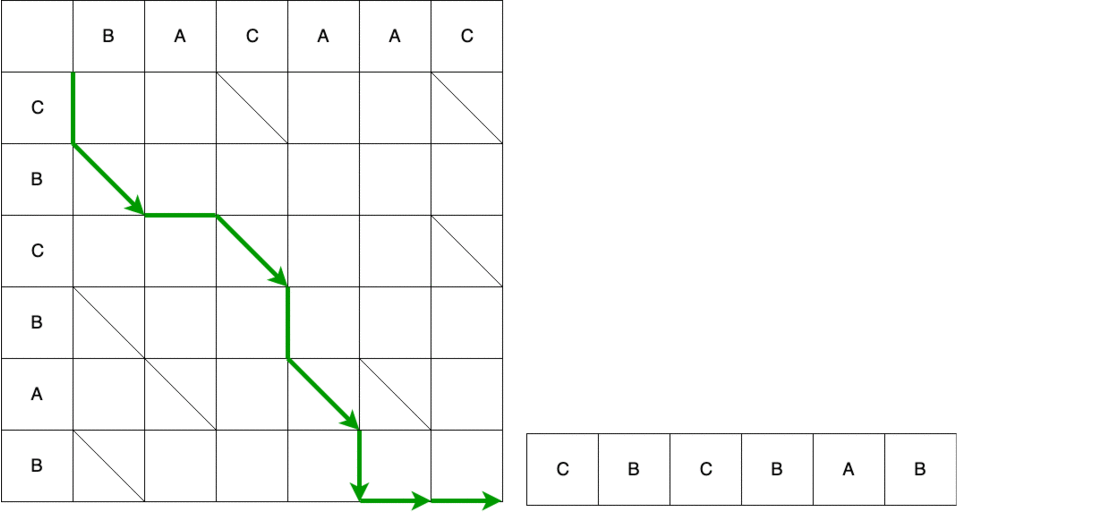
Результатом работы алгоритма Майерса является скрипт с набором минимального количества действий, которые надо сделать для преобразования одной последовательности в другую. В DiffUtil алгоритм Майерса используется для поиска разных элементов, которые определяются методом areItemsTheSame(). Помимо формирования списка змеек, при прохождении по спискам алгоритмом Майерса создаются списки статусов элементов старого и нового списков. Все эти данные, а также флаг detectMoves и реализованный пользователем callback передаются в конструктор DiffResult(Callback callback, List<Snake> snakes, int[] oldItemStatuses, int[] newItemStatuses, boolean detectMoves).

Пока я писал эту статью, удалось раскопать что именно происходит в DiffResult: алгоритм проходится по змейкам и выставляет элементам флаги(в списки статусов), по которым определяется что именно произошло с элементом. По этим флагам во время применения изменений к RecyclerView определяется каким методом применять обновления: notifyItemRangeInserted, notifyItemRangeRemoved, notifyItemMoved и notifyItemRangeChanged. Более подробно я расскажу об этом в следующий раз.

Ссылки 

• The Myers Diff Algorithm and Kotlin Observable Properties — здесь помимо ознакомления с алгоритмом Майерса приводятся интересные фичи Kotlin для упрощения работы с DiffUtil.
• The Myers Diff Algorithm part 1 – цикл статей, который начинает объяснение алгоритма Майерса на пальцах и постепенно переводит его на математический язык.
• An O(ND) Difference Algorithm and Its Variations – официальная научная статья алгоритма Майерса.