
В 1985 году Институт инженеров электротехники и электроники (IEEE) установил стандарт IEEE 754, отвечающий за форматы чисел с плавающей запятой и арифметики, которому суждено будет стать образцом для всего железа и ПО на следующие 30 лет.
И хотя большинство программистов использует плавающую точку в любой момент без разбора, когда им нужно проводить математические операции с вещественными числами, из-за определённых ограничений представления этих чисел, быстродействие и точность таких операций часто оставляют желать лучшего.
Много лет стандарт подвергался резкой критике со стороны специалистов по информатике, знакомых с этими проблемами, однако больше всего среди них выделялся Джон Густафсон, в одиночку ведший крестовый поход с целью замены плавающей запятой на что-то более подходящее. В данном случае более подходящим вариантом считается posit или unum – третий вариант результата его исследования «универсальных чисел». Он говорит, что числа формата posit решат большинство главнейших проблем стандарта IEEE 754, дадут улучшенную производительность и точность, и при этом будут использовать меньше битов. Что ещё лучше, он заявляет, что новый формат может заменить стандартные числа с плавающей запятой «на лету», без необходимости менять исходный код приложений.
Мы встретились с Густафсоном на конференции ISC19. И для находящихся там специалистов, занимающихся суперкомпьютерами, одно из главных преимуществ формата posit состоит в том, что можно достичь большей точности и динамического диапазона, используя меньше битов, чем числа из IEEE 754. И не просто немного меньше. Густафсон сказал, что 32-битный posit заменяет 64-битное float почти во всех случаях, что может иметь серьёзные последствия для научных вычислений. Если уполовинить количество битов, можно не только уменьшить объёмы кэша, памяти и хранилища для этих чисел, но и серьёзно уменьшить ширину канала, необходимого для передачи их на процессор и обратно. Это главная причина, по которой арифметика на базе posit, по его мнению, даст от двойного до четверного ускорения расчётов по сравнению с числами с плавающей запятой от IEEE.
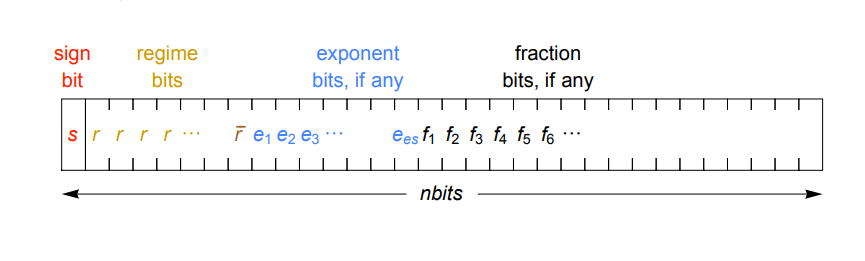
Ускорения можно будет достичь через уплотнённое представление вещественных чисел. Вместо экспоненты и дробной части фиксированного размера, используемой в стандарте IEEE, posit кодирует экспоненту переменным количеством бит (комбинацией битов режима и битов экспоненты), так, что в большинстве случаев их требуется меньше. В итоге на дробную часть остаётся больше битов, что даёт большую точность. Динамическую экспоненту стоит использовать благодаря её сужающейся точности. Это означает, что величины с небольшой экспонентой, которые чаще всего используются, могут иметь большую точность, а реже используемые очень крупные и очень мелкие числа будут иметь меньшую точность. Работа Густафсона от 2017 года, описывающая формат posit, даёт подробное описание того, как это работает.
Ещё одно важное преимущество формата в том, что, в отличие от обычных чисел с плавающей запятой, posit дают одинаковые побитовые результаты на любой системе, чего часто нельзя гарантировать с форматом от IEEE (тут даже одинаковые вычисления на одной и той же системе могут дать разные результаты). Также новый формат расправляется с ошибками округления, переполнением и исчезновением значащих разрядов, денормализованными числами, и множеством значений типа not-a-number (NaN). Кроме того, posit избегает такой странности, как несовпадающие значения 0 и -0. Вместо этого формат использует для знака двоичное дополнение, как у целых чисел, что означает, что побитовое сравнение будет выполняться правильно.
С числами posit связано нечто под названием quire – механизм накопления, позволяющий программистам выполнять воспроизводимую линейную алгебру – процесс, недоступный обычным числам формата IEEE. Он поддерживает обобщённую операцию совмещённого умножения-сложения и другие совмещённые операции, позволяющие вычислять скалярные произведения или суммы без ошибок округления или переполнений. Тесты, запущенные в Калифорнийском университете в Беркли, продемонстрировали, что операции quire проходят в 3-6 раз быстрее, чем последовательное их выполнение. Густафсон говорит, что они позволяют числам posit «драться за пределами своей весовой категории».
Хотя этот формат чисел существует всего пару лет, в сообществе специалистов по высокопроизводительным вычислениям (HPC) уже есть интерес к изучению возможностей их применения. В настоящий момент вся работа остаётся экспериментальной, и основана на предполагаемом быстродействии будущего железа или на использовании инструментов, эмулирующих posit-арифметику на обычных процессорах. Пока в производстве нет чипов, реализующих posit на аппаратном уровне.
Одно из потенциальных применений формата – строящийся радиоинтерферометр Square Kilometer Array (SKA), при проектировании которого рассматривают числа posit как способ кардинально уменьшить ширину канала и вычислительную нагрузку для обработки данных, поступающих с радиотелескопа. Необходимо, чтобы обслуживающие его суперкомпьютеры потребляли не более 10 МВт, и один из наиболее многообещающих способов достичь этого, по мнению проектировщиков, — использовать более плотный формат posit для того, чтобы вдвое урезать предполагаемую ширину канала памяти (200 ПБ/сек), канала передачи данных (10 ТБ/сек) и сетевого соединения (1 ТБ/сек). Вычислительная мощность также должна возрасти.
Ещё одно применение – использование в предсказаниях погоды и прогнозированиях климата. Британская команда показала, что 16-битные числа posit явно опережают стандартные 16-битные числа с плавающей запятой, и у них «есть прекрасный потенциал для использования в более сложных моделях». 16-битная эмуляция posit в этой модели работала так же хорошо, как 64-битные числа с плавающей запятой.
Ливерморская национальная лаборатория оценивает posit и другие форматы чисел, изучая возможности уменьшения количества перемещаемых данных в эксафлопсных суперкомпьютерах будущего. В некоторых случаях у них тоже получились лучшие результаты. К примеру, числа posit смогли дать превосходящую точность в таких физических расчётах, как ударная гидродинамика, и в целом опередили числа с плавающей запятой в различных измерениях.

Возможно, наибольшими возможностями posit будут обладать в области машинного обучения, где 16-битные числа можно использовать для обучения, а 8-битные – для проверки. Густафсон сказал, что для обучения 32-битные числа с плавающей точкой являются перебором, и в некоторых случаях они даже не демонстрируют таких хороших результатов, как 16-битные posit, пояснив, что стандарт IEEE 754 «абсолютно не был предназначен для использования с ИИ».
Неудивительно, что на них обратило внимание и ИИ-сообщество. Джефф Джонсон из Facebook разработал экспериментальную платформу с FGPA при помощи posit, демонстрирующую лучшую энергоэффективность по сравнению как с float16, так и с bfloat16 от IEEE на задачах по машинному обучению. Они планируют исследовать использование 16-битных аппаратных quire для обучения и сравнить их с конкурирующими форматами.
Стоит отметить, что Facebook работает с Intel над процессором Nervana Neural Network (NNP), который должен ускорить некоторые из задач социального гиганта, связанные с ИИ. Не исключается вариант использования формата posit, хотя более вероятно, что Intel оставит для Nervana его изначальный формат FlexPoint. В любом случае, этот момент стоит отслеживать.
Густафсону известно, по крайней мере, об одном ИИ-чипе, в котором пытаются использовать числа posit при проектировании, хотя он не имеет права разглашать названия компании. Французская компания Kalray, работающая с инициативой European Processor Initiative (EPI), также продемонстрировала интерес в поддержке posit в их ускорителе следующего поколения Massively Parallel Processor Array (MPPA), поэтому эта технология может попасть на европейские эксафлопсные суперкомпьютеры.
Густафсона всё это, естественно, вдохновляет, и он считает, что эта третья попытка продвижения его универсальных чисел может увенчаться успехом. В отличие от версий один и два, posit легко реализовать в железе. А учитывая яростную конкуренцию в области ИИ, возможно, стоит ожидать коммерческого успеха нового формата. Среди других платформ, на которых posit может ожидать блестящее будущее – цифровая обработка сигналов, GPU (для графики и других вычислений), устройства для интернета вещей, edge computing. И, конечно же, HPC.
Если технология получит коммерческое распространение, Густафсон вряд ли сможет заработать на её успехе. Его проект, как указано в 10-страничном стандарте, полностью открыт, и доступен для использования любой компанией, желающей разработать соответствующие ПО и железо. Что, вероятно, объясняет внимание к технологии со стороны таких компаний, как IBM, Google, Intel, Micron, Rex Computing, Qualcomm, Fujitsu, Huawei и многих других.
Тем не менее, замена IEEE 754 чем-то более подходящим – огромнейший проект, даже для человека с таким впечатляющим резюме, как у Густафсона. Ещё до того, как поработать в ClearSpeed, Intel и AMD, он изучал способы улучшения научных расчётов на современных процессорах. «Я пытался разобраться в этом вопросе последние 30 лет», — сказал он.
Комментарии (127)

e_fail
06.08.2019 10:39IEEE (тут даже одинаковые выичлсения на одной и той же системе могут дать разные результаты)
Можно примерчик?
kasyachitche
06.08.2019 10:44+1На хабре была статья об этом.
habr.com/ru/company/intel/blog/205970
И вот вам пример.
habr.com/ru/company/intel/blog/205970/#comment_7117974
e_fail
06.08.2019 11:35По вашим ссылкам разные результаты получены ввиду _разных_ вычислений. (Ещё популярная в своё время история из той же оперы — 10 битные регистры в 8087). IEEE тут ни при чём.

npocmu
06.08.2019 11:58Сорри за занудство, но где все-таки пример одинаковых вычислений?
Все ваши ссылки поясняют тривиальную вещь: разный порядок вычисления выражения дает разные результаты.
ainoneko
06.08.2019 12:32Сорри за занудство, но где все-таки пример одинаковых вычислений?
Вот, например: "Math.Round returns different values for the same input.". ?\_(?)_/?

nobodysu
06.08.2019 13:12toster.ru/q/636091
Ссылки внизу.
e_fail
06.08.2019 13:56Сходил по первой ссылочке.
Why, you ask, can that happen? Good question; thanks for asking. Here’s the answer (with emphasis on the word “often”; the behavior depends on your hardware, compiler, etc.): floating point calculations and comparisons are often performed by special hardware that often contain special registers, and those registers often have more bits than a double. That means that intermediate floating point computations often have more bits than sizeof(double), and when a floating point value is written to RAM, it often gets truncated, often losing some bits of precision.
Это не про IEEE754. Это про то, как инженеры, делавшие конкретную платформу, хотели как лучше, а устроили всем геморрой. С 8087, например, такая история.
Остальные будем разбирать, или сами осилите?
marat_zh
07.08.2019 01:01Насколько я знаю, 8087 сделали до того, как был оформлен стандарт IEEE754. И это стандарт делали ориентируясь на этот сопроцессор, а не наоборот. Поэтому, наверное, такая несостыковка.

bopoh13
07.08.2019 20:35В заключении статьи об экспоненциальном представлении чисел сказано, что все проблемы аппаратные. Выбор неверного представления числа может приводить к ошибкам в вычислениях.

irbis_al
06.08.2019 11:01+1Вот тут на sql.ru обсуждалось, что Oracle pl/sql даже при перестановке мест множителя дает различные результаты
sql.ru Oracle форум
e_fail
06.08.2019 11:37+1Представьте себе, операции с плавающей точкой — не ассоциативны и не дистрибутивны. Но это не проблема IEEE. Если вы поставите скобочки одинаково, результат всегда будет одинаковым.

knotri
06.08.2019 15:17А как воспроизвести ?
Я попробовал вот так в консоле браузера — ноль консоль логов произошло
for (let i = 0 ; i < 10e6; i++) { let x = Math.random() * 10e8; let y = Math.random() * 10e8; let z = Math.random() * 10e8; if (x*(y + z) !== (z + y) *x) { console.log({x,y}) } }
ShadowTheAge
06.08.2019 15:42+1То что вы проверили это коммутативность (а не ассоциативность и не дистрибутивность)
Ассоциативность:
(1e-200*1e200)*1e200 => 1e+200
1e-200*(1e200*1e200) => Infinity
Дистрибутивность:
1e200*(1e200-1e200) => 0
(1e200*1e200)-(1e200*1e200) => NaN

ainoneko
06.08.2019 18:14Я взял поменьше (до 1e6) и проверил дистрибутивность
check_math.jsfor (let i = 0 ; i < 1e6; i++) { let x = Math.random() * 10e8; let y = Math.random() * 10e8; let z = Math.random() * 10e8; if (x*(y + z) !== x*z + y*x) { console.log({x,y}) } }

wadeg
07.08.2019 00:21Оракловый number — это не только не IEEE 754, но и вообще не плавающая точка, а вовсе даже разновидность BCD. Так что примерчик — он о другом.

mynameco
06.08.2019 20:02Был описан случай, не могу найти статью =( там проблема была в том, что один и тот же бинарный код может использовать большие регистры а может и нет, зависит от того в какой поток улетело вычисление и какие ресурсы доступны конкретному потоку. И лечилось это афинити на конкретный поток.

Pand5461
06.08.2019 11:37+1Это означает, что величины с небольшой экспонентой, которые чаще всего используются, могут иметь большую точность, а реже используемые очень крупные и очень мелкие числа будут иметь меньшую точность.
И вот на этом возникает смутное ощущение, что равенство 32-битного Posit и 64-битного IEEE во всех-всех задачах есть только на бумаге...
Например, лёгкая манипуляция из того же отчёта LLNL:

Глядите, как всё хорошо — в трёх случаях из четырёх Posit даёт лучшую точность, чем IEEE single float. Но: давайте подумаем, а в какой реальной задаче будет нужно расстояние до звезды и какие масштабы будут с ним соседствовать? И получаем, что в реальной задаче рядом, вероятно, будет, либо астрономическая единица, либо порядок диаметра галактики. Поэтому все четыре примера, по сути, не отражают реальную сферу применения.
При этом: с привычным IEEE float у меня будет моя относительная погрешность 10-7 вне зависимости от того, решу я расстояние выражать в световых годах или километрах. А адаптивное число бит в экспоненте выглядит как много-много радости по поводу выбора масштабов в реальных вычислительных задачах.
Victor_koly
06.08.2019 12:37Я не помнимаю, как такая ошибка с 1e51 длин Планка могла выйти. Это тип 64-битный или 32ух?

Pand5461
06.08.2019 13:46На этом слайде 32-битные представления сравниваются.
На 64 битах Posit в обоих последних примерах, видимо, будет хуже, т.к. в IEEE экспонента всего 11 бит.
Victor_koly
06.08.2019 13:57Тогда они пробуют умножить на число, которое не входит в диапазаон значений 4-байтного Float. Логично, тчо у них вышел какой-то бред.

Pand5461
06.08.2019 15:19Ну вот они и показывают, что в single float будет уже бред, а posit хоть как-то, но держится. Другой вопрос — кому реально понадобится в программе расстояние между звёздами в планковских длинах выражать?

defuz
06.08.2019 18:37Потому что в научных вычислениях у вас регулярно вылезают очень маленькие и очень большие значения и posit c ними лучше справляется не только из-за увеличенного диапазона, но и из-за отличной от float стратегии underflow/overflow.
Лучше справляется – это не разрушает цепочку вычислений, деградируя до NaN или ±Infinity.
Al_Azif
07.08.2019 01:58+1Да не только в астрономических вычислениях, что вы вцепились в них.
Возьмите любую игру: на зуме вылезают глюки Z-buffer'а из-за проблем с точностью вычислений на больших дистанциях (из-за того что вся геометрия вгоняется в один юнит в итоге после матричных перемножений. В смысле область размером 1x1x1 юнит)
То же самое у софтовых рендереров, когда, скажем, у горе-ахренетектора, (который не знает и не должен знать ничего о флоатах), здание находится в сцене в 2 млн сантиметров от нуля(по плану!) и рендерится «зубьями» (ошибка нахождения пересечения луча с треугольником, находящимся куда Макар гусей не гонял).
OpenEXR с его half-float спасибо тоже скажет.
PS: Кому-то выше отвечал, так получилось.

ggreminder
06.08.2019 23:58В научных вычислениях, как учил нас наш завкафедры, главное — количество значащих цифр. И любые операции на больших числах имеют точность наименьшего числа. Например, звезда находится на расстоянии 100,5 парсек.
1 парсек = 3,2615637772… светового года
100,5*3,2615637772… = 331,6 (100,5*3.3) светового года
Хотя «точное» произведение будет равно 327,7871596…
А вот 100,500 парсек, где 500 — значащие цифры из измерений, будет уже 327,831 светового года.
Аналогично с очень большими экспонентами — при умножении мантиссы складываются, а точность дробной части равна точности наименьшей из перемножаемых.
chersanya
07.08.2019 01:17Странно по вашему подходу получается — (100.5+-0.1) * 3.2615… = 327.78 +- 0.33, и ваше 331.6 в этот диапазон вообще не входит.

ggreminder
07.08.2019 04:29Вы, опять же, берете много цифр во втором числе, поэтому и не сходится.

chersanya
07.08.2019 05:16А с чего их меньше брать, это число ведь известно с большой точностью? Изначальные данные: расстояние 100.5 +- 0.1 парсек (вы ведь это подразумевали под словами «одна значащая цифра после запятой»?). Вопрос: чему равно расстояние в световых годах? Ответ — 327.78 +- 0.33, как ни крути.
То есть, мы по исходным данным точно знаем, что расстояние никак не равно 331.6 светового года — оно меньше.
khim
07.08.2019 11:37Успокойтесь, вы оба правы. Ваш собеседник так всё классно, аккуратно, написал… а потом обрубил 3,2615637772 до 3,3 (две значащих цифры вместо четырёх, как в 100,5) и получил чушь.
Не знаю, что он хотел доказать, но показал только лишь то, что правила нужно не только зубрить, но и понимать.
michael_vostrikov
08.08.2019 00:01Общее количество значащих цифр к ошибке, о которой он говорит, не имеет отношения. Если точность измерений одна десятая парсека, то она и будет одна десятая парсека, неважно 100 там парсеков или 1000000. И погрешность после умножения соответственно будет одна и та же.
Другое дело, что умножение флоатов в фиксированной разрядной сетке с этим тоже не связано. Там да, все значащие цифры важны. Пока влазим в разрядную сетку, относительные величины множителей вообще не имеют значения.

khim
08.08.2019 00:52И погрешность после умножения соответственно будет одна и та же.
Нет, не одна и та же. Точность, с которой известно второе слагаемое тоже влияет. Причём если мы урожаем, то влияет именно относительная точность (назад в школу, изучать как связаны умножение, сложение и логарифмы).
michael_vostrikov
08.08.2019 10:121.5 +- 0.1 ?x = 0.1/1.5 ~= 0.0667 100.5 +- 0.1 ?x = 0.1/100.5 ~= 0.001 1000000.5 +- 0.1 ?x = 0.1/1000000.5 ~= 0.0000001 3.2615637772 ?x ~= 0% 1.5 (0.0667) * 3.2615637772 (0) = 4.8923456658 (0.0667) ?x = x * ?x = 4.8923456658 * 0.0667 = 0.32631945590886 ~= 0.33 100.5 (0.001) * 3.2615637772 (0) = 327.7871596086 (0.001) ?x = x * ?x = 327.7871596086 * 0.001 = 0.3277871596086 ~= 0.33 1000000.5 (0.0000001) * 3.2615637772 (0) = 3261565.4079818886 (0.0000001) ?x = x * ?x = 3261565.4079818886 * 0.0000001 = 0.32615654079818886 ~= 0.33

pal666
07.08.2019 01:23а завкафедры не учил вас, что значащие цифры начинаются с первой, а не после запятой(т.е. что в 100.5 их 4, а в 3.3 2)?

ggreminder
07.08.2019 04:32-1Имелись в виду только значащие цифры в дробной части. То есть, если одна величина известна с точностью до десятых, то и ответ будет дан с такой же точностью, не более.

khim
07.08.2019 11:39+3Рекомендую сходить к вашему завкафедрой, чтобы он у вас принятый зачёт отменил.

michael_vostrikov
08.08.2019 00:01В целом да, но вроде бы знаки отбрасываются после точного умножения, а не до.

ggreminder
08.08.2019 00:16Возможно, вы правы. Выше со мной не согласились, но я не смог вспомнить точную формулировку, чтобы ответить. Это было лет 15 назад, да и переспросить уже не у кого…

khim
08.08.2019 00:57Найти где-то в шкафу или даже в интернете логарифмическую линейку. Смотреть, думать. Наступит просветление.

khim
08.08.2019 00:55Знаки можно отюрасыаать и до и после. В 60е годы, когда вычисления делались на логарифмической линейке и трудоёмкость вычислений ощущалась «попом» про то как и когда это делать знали все инжинеры. Сейчас же про это забыли…

pal666
08.08.2019 20:34а вы научную запись ( en.wikipedia.org/wiki/Scientific_notation ) используйте и тогда все станет на свои места. ведь точность не меняется от формы записи?

wormball
06.08.2019 14:45Я так понял, много-много радости по поводу того, что можно будет совмещать плюсы фиксированной точки и плавающей точки. Один раз выбираем масштаб (причём, как правило, люди и так стараются считать в районе единицы) и считаем, не трясясь каждый раз, что где-то может быть переполнение (как в случае фиксированной точки).
> И получаем, что в реальной задаче рядом, вероятно, будет, либо астрономическая единица, либо порядок диаметра галактики.
Что-то мне подсказывает, что диаметрами галактики вряд ли будут считать, скорее уж метрами. Хотя, конечно, примеры «меньше единицы» надо было привести.
Pand5461
06.08.2019 15:35Я про то, что они привели сферический парсек в вакууме как пример.
posit, судя по описанию, работает через размен порядка на мантиссу. Поэтому числа вблизи 1 имеют больше значащих разрядов в мантиссе, а чем дальше, тем меньше.
Вопрос — если в реальной задаче за базовую единицу измерения взят парсек, то какие там будут встречаться характерные цифры? Насколько мне известно, это будет либо порядка 10-5пк (т.е. астрономической единицы), либо порядка 103-6пк (диаметр галактики).
Вывод: парсек как характерный масштаб вообще-то не очень полезен для применения с posit-числами. Только вот обычный float прожуёт и симуляцию планетной системы с расстояниями в парсеках, и симуляцию галактики, и не подавится. При этом программисту не нужно прилагать никаких усилий, чтобы специально обезразмерить задачу.
Так что представление это очень и очень нишевое, как мне кажется.
defuz
06.08.2019 18:27Если вас не волнует всерьез энергоэфективность и скорость вычислений – то да. А вот в среде научных вычислений posit достаточно горячо обсуждается.
> Только вот обычный float прожуёт и симуляцию планетной системы с расстояниями в парсеках, и симуляцию галактики, и не подавится. При этом программисту не нужно прилагать никаких усилий, чтобы специально обезразмерить задачу.
Это до тех пор пока у вас в одном из вычислений не вылезет ±Infinity или NaN. Или накопление ошибки до неузнаваемости исказит результат. В этом смысле как раз posit с большей вероятностью прожует симулацию галактики: у него другая стратегия underflow/overflow так что необычайно маленькое расстояние между двумя телами не приведет к делению на 0 и в конце вычислений на вас не будет смотреть NaN.
DrSmile
06.08.2019 20:13+1Обычные флоаты честно выдерживают требуемую точность (исключение — underflow), либо выдают «не шмогла». Поситы же дают какой-то ответ всегда, деградируя при этом точность до нуля. Собственно, прямая аналогия программистских стратегий «сразу падаем при обнаружении бага» и «любой ценой выдаем хоть что-то, у нас же надежное приложение!»
так что необычайно маленькое расстояние между двумя телами не приведет к делению на 0 и в конце вычислений на вас не будет смотреть NaN
Вот только ответ, который дадут поситы может на пару порядков отличаться от точного математического. И никакой возможности сказать — это более-менее точный ответ или практически случайное число, нет. Обычные флоаты тоже страдают от данной проблемы, но в гораздо меньшей степени.
Еще поситы обсуждали на gamedev.ru. Лично я для себя вынес, что поситы непригодны для сколь-нибудь серьезных применений.
defuz
06.08.2019 20:38Обычные флоаты честно выдерживают требуемую точность (исключение — underflow), либо выдают «не шмогла».
Выдерживают требуемую точность они ровно в рамках одной операции, а дальше накопление ошибки может завести вас буквально куда угодно.
Поситы же дают какой-то ответ всегда.
Не всегда. Деление на 0 – это ошибка (±inf), операция над ±inf – это тоже ±inf.
деградируя при этом точность до нуля
Это голословное утверждение. Нужно рассматривать конкретные примеры. На практике выходит так что там где float из-за одной из тысячи последовательных операций (например, a1*b1 + a2*b2 + ...) свалился в NaN/inf/0, posit даст приемлемый с точки зрения точности результат.
Вы же скорее описали ситуацию когда тупо неверно выбрана размерность для вычислений. Тут вам никакая магия не поможет.
Вот только ответ, который дадут поситы может на пару порядков отличаться от точного математического.
Может, как и в случае с float.
И никакой возможности сказать — это более-менее точный ответ или практически случайное число, нет.
Если вам нужно не только произвести вычисление, но и гарантировать его точность – был придуман тип Valids (одна из вариаций Posit), которая на любую операцию возвращает не просто значение, а диапазон, в котором реальное значение гарантированно лежит.
Правда, эта идея не получила широкой поддержки, поскольку оказалось что там где требуется гарантировать точность, практичнее использовать Quire (другой формат операций над Posit), которые просто не теряют точность во время операций суммирования/умножения.
Так что с одной стороны не рекомендую делать выводы только по gamedev.ru, с другой – позиты действительно на сегодняшний день бесполезны, если только вы не планируете производить свое железо. Аппаратной поддержки нигде нет, а софтварная эмуляция не сравнима с апаратной реализацией float. Так что пока можно применять разве что для эфективного сжатия чисел с потерей точности.
DrSmile
06.08.2019 21:54Выдерживают требуемую точность они ровно в рамках одной операции, а дальше накопление ошибки может завести вас буквально куда угодно.
Накопление погрешности — это отдельная проблема. И как раз анализ на численную неустойчивость в случае поситов на порядок сложнее из-за их плавающей точности.
Вы же скорее описали ситуацию когда тупо неверно выбрана размерность для вычислений. Тут вам никакая магия не поможет.
Вот как раз про это я и пишу. Обычные флоаты нечувствительны к небольшой неидеальности выбора погрешности, часто можно хоть на 10 порядков вверх или вниз сдвигать без какой-либо деградации результата. У поситов же даже один десятичный порядок сдвига от единицы может привести к потере точности.
Аппаратной поддержки нигде нет
И неудивительно. Я на gamedev.ru как раз разбирал этот вопрос.
yleo
06.08.2019 22:34Всё верно, но...
Поситы — это чтобы меньше потерять при сохранении некого float-результата в меньшем кол-ве бит.
В сравнении с 754 поситы теряют они действительно меньше, но иначе.
При неправильном использовании, ни 754, ни поситы не спасут.
Однако, при правильном использовании поситы позволяют потерять меньше.
А статья дурная, начиная с заголовка.
Интерферометр тоже за уши притянут — при их объемах и бюджете можно ASIC-и использовать для delta-кодирования и т.п.

defuz
06.08.2019 23:52Обычные флоаты нечувствительны к небольшой неидеальности выбора погрешности, часто можно хоть на 10 порядков вверх или вниз сдвигать без какой-либо деградации результата. У поситов же даже один десятичный порядок сдвига от единицы может привести к потере точности.
Не понимаю откуда вы это взяли. У позитов есть стандартные варианты по аналогии с fp16, fp32, fp64 – p8e0, p16e1, p32e2. Если вы тупо замените fp32 на p32e2 вряд ли у вас будет деградация результата из-за того что вы что-то там не откалибровали. Можем проверить.
DrSmile
07.08.2019 02:44Не понимаю откуда вы это взяли.
Да прямо из исходной статьи про поситы. Там есть красивый график точности для разных вариантов представления чисел. У стандартных флоатов ровный забор, а у поситов треугольник — в районе 1 они, действительно, точнее, но шаг влево или вправо от «вершины» и они начинают проигрывать.
defuz
07.08.2019 02:51Вы же в курсе по оси X там логарифмическая шкала? Шаг влево или вправо после которых они начинают проигрывать это несколько десятков порядков.

DrSmile
07.08.2019 03:26Двоичные порядки там. Более конкретно, каждые 2es двоичных порядков теряется одна двоичная цифра мантиссы. Т. е. для p32e2 каждые 4 двоичных порядка (сдвиг от единицы в 16 раз) мы теряем половину точности. Т. к. в районе 1 там мантисса 27 бит, то чтобы сравняться с флоатами надо потерять 4 цифры, т. е. оказаться в районе 164 = 65536. А в районе миллиона точность станет хуже флоатов.

defuz
07.08.2019 03:40Точность станет хуже лишь на 1 бит (с 24 до 23). И еще на один бит она станет хуже уже после 4 миллиардов. Ну как бы да. Это цена, которую приходится платить за то чтобы иметь горазо более высокую на числах в диапазоне 1/268435456 — 268435456.

Pand5461
07.08.2019 11:58Как я понял, DrSmile всё-таки прав.
8 бит на показатель в es2 требуются начиная с 11111000, и это (5-1)*22 + 0 = 16, а 216 — это 65536. Начиная с 220 точность ниже, чем у float. А ещё на один бит она станет хуже после 224, это далеко не 4 миллиарда.
defuz
07.08.2019 15:12DrSmile изменил комментарий, я исходил из его расчетов. Перепроверил на конкретных числах – вы правы. До 2^20 точность posit лучше или такая же, после 2^20 она становится чуть ниже, и так далее.
Как я уже говорил, это плата за большую точность внутри диапазона. В центре диапазона у вас будет 4 дополнительных бита точности, так что пока большинство ваших значений лежит в интервале 1/2^20..2^20, а это диапазон в 12 десятичных порядков, точность ваших вычислений будет выше всегда.
На практике можно работать в гораздо более широком диапазоне, потому что точность деградирует достаточно медленно, и эта деградация компенсируется большей точностью на остальных числах. Здесь уже не имея конкретной задачи невозможно говорить какой подход проявит себя лучше.

Pand5461
07.08.2019 01:33+1Меня волнует то, в первую очередь, что распространение ошибки при фиксированной длине мантиссы достаточно просто проанализировать.
У меня как-то Inf-ы и NaN-ы вылезали, в основном, из-за catastrophic cancellation при вычитании (Inf от x/0 и NaN от 0/0). А от него не видно, как posit систематическим образом спасает.
Отсутствие инвариантности по масштабу напрягает. С Float32/64 я могу знать, что(2.0 * x) / (3.0 * x)отличается от2.0 / 3.0разве что последним битом (при разумных значенияхx, естественно). У posit с этим как-то непонятно.
И главный вопрос, который у меня возник — я верно понял, что удвоение порядка — это плюс два бита в порядок и, соответственно, минус два из мантиссы? Если да, то более широкая мантисса по сравнению с IEEE там всё-таки в довольно узком диапазоне значений будет, и как-то ей хвастаться некорректно...
defuz
07.08.2019 02:01-1У меня как-то Inf-ы и NaN-ы вылезали, в основном, из-за catastrophic cancellation при вычитании (Inf от x/0 и NaN от 0/0). А от него не видно, как posit систематическим образом спасает.
На самом деле как раз спасает систематически отличной от float стратегией underflow/overflow. Вы никогда не получите ±Infinity складывая, вычитая или умножая числа, отличные от ±Infinity. Вы никогда не получите ноль, поделив любое число отличное от нуля на любое другое число. На первый взгляд это звучит дико, но нужно понимать что понятия чисел в системе posit отличаются от чисел в системе float.
С Float32/64 я могу знать, что (2.0 * x) / (3.0 * x) отличается от 2.0 / 3.0 разве что последним битом (при разумных значениях x, естественно). У posit с этим как-то непонятно.
Точность будет выше, поскольку числа 2 и 3 имеют порядок близкий к единице. Причем, как количество идентичных результатов будет выше, так и погрешность в случае ошибки будет меньше.
И главный вопрос, который у меня возник — я верно понял, что удвоение порядка — это плюс два бита в порядок и, соответственно, минус два из мантиссы?
Скорее всего не верно. В рамках одной и той же системы в posit мантисса может занимать разное количество бит, и даже 0 бит. Это определятся значением regime – количеством первых последовательных бит, которые равны друг другу. Это немного сложная концпеция, которую сходу не объяснить, но основная суть в том что для разных значений мантисса будет иметь разную размерность.

defuz
07.08.2019 02:16Чтобы мои слова не выглядели голословными, привожу анализ ошибки сумирования и деления на всем пространстве чисел для posit и float:
Cуммирование:

Деление:

В вашем случае ситуация еще лучше, потому что 2 и 3 — удобные числа для posit.
DrSmile
07.08.2019 03:09-2Вот как раз эти графики — это самое большое вранье из той статьи: они показывают только самый хвост распределения с самыми большими ошибками. Кого, вообще, волнует, что вносимая ошибка не 1.5%, а целых 1%? В обоих случаях результат идет в мусорку. Самая интересная часть этого графика — это там где decimal error порядка 10-8, где и происходит большая часть реальных вычислений. И уж тем более, exact там или inexact никого не интересует.

defuz
07.08.2019 03:16А вы до следующей страницы уже долистали? Потому что этот график – как раз начало с наименьшими ошибками, целиком график выглядит так:

И прежде чем писать про 1%-1.5% процента разберитесь что такое decimal error. Ошибка в 1% это decimal error = 0.004. И разберитесь что здесь находится по оси X.
DrSmile
07.08.2019 03:37Там во всей статье нет ни одного графика с decimal error в стандартном диапазоне точности (10-8 для 32-битных флоатов).
Ошибка в 1% это decimal error = 0.004
Сорри, пропустил нолик. Правильное утверждение: «кого волнует, что ошибка 15%, а не целых 10%?».
defuz
07.08.2019 03:48Подскажите, как по вашему должен выглядеть такой график? Что по X, что по Y.

DrSmile
07.08.2019 04:01Нужна его часть в районе нуля, увеличенная в ~108 раз. А по X там, фактически, условные единицы, так что, вообще, неважно.

defuz
07.08.2019 04:11Куда еще его увеличивать? Это графики для восьмибитных чисел. На графике отображены все возможные 65536 результата вычислений. До значения ~16000 по оси X у позитов значение по Y тупо 0. У флоатов оно нулевое первые ~12000 значений. Линия позитов идет ниже линии флоатов для любого X.
Если вы хотите увидеть там какой-то сюрприз, его там не будет. Точность float8 это 3 бинарных порядка мантисы (1/16), а значит в наихудшем случае decimal error = log10 (1+1/16)/1 = 0.02632. Ровно в это значение флоаты и упираются на графике.
DrSmile
07.08.2019 05:22-1Это графики для восьмибитных чисел.
Ну тогда это еще одна подтасовка, ибо 8-битных IEEE-float, в принципе, не существуют. И нигде нету сравнений с реальными 32/64-битными флоатами. Почему они взяли 3-битную мантиссу и 4-битную экспоненту, а не наоборот? Наверное, потому что иначе графики не такие красивые получались.
defuz
07.08.2019 17:50Почему они взяли 3-битную мантиссу и 4-битную экспоненту
Чтобы порядок экспонент был хоть как-то сравним.
Держите сравнение f32 и p32e2. Построено методом Монте-Карло на одном миллионе сэмплов.


DrSmile
07.08.2019 21:45-1Во, уже виден трейдофф, уже не все так однозначно. Только теперь выглядит, как убедительная победа стандартных флоатов над поситами, хотя там, по идее, около нуля поситы должны вырываться вперед снова. Наверное, надо в логарифмическом масштабе строить, одного логарифма в decimal error мало.

defuz
07.08.2019 21:52На этом графике, как и на графике в статье значения по X отсортированы в соответствием со значением Y – от наименьшей ошибки к наибольшей. Так что возле нуля ничего интересного не происходит.
Я здесь вижу обратную сторону медали: у позитов наростание ошибок очень плавное и напоминает ужатую гиперболу. Это означает что аномально большие ошибки будут встречаться гораздо реже. У флоатов же 20% суммирований заканчивается с рандомной точностью.
Pand5461
07.08.2019 22:48А вы не знаете, случаем, почему Густафсон предлагает настолько жмотиться и делать стандартными p32es2?
Я тут прикинул, es3 лучше почти по всем параметрам, кроме потери одного бита в диапазоне от 1/16 до 16. Но блин, это уже нужно очень сильно заморочиться, чтобы в алгоритме важные переменные за этот диапазон гарантированно не вышли.
А дальше там более-менее прилично — точность не ниже float32 на диапазоне 18 десятичных порядков, и потом не так радикально падает.
"Не так радикально", правда, это число незначащих цифр O(|log2x|), как и в денормализованных float, только константа в es раз меньше (т.к. порядок в унарной форме записывается по сути).
defuz
07.08.2019 23:26Как-то вы не правильно посчитали, или я вас не так понял. У p32e3 в сравнении с p32e2 точность хуже, а диапазон в два раза шире (2^-240… 2^240).
Для es=3 у нас шаг не 16 бит, а 256 (2^2^es).
Pand5461
08.08.2019 00:05Точность же хуже только для тех чисел, у которых в es2 один бит режима — это порядки от 0100 (-4) до 1011 (3). Это числа от 1/16 до 16. До 7 порядка (10111 es3, 11011 es2), т.е. до 256, точность одинаковая. А дальше es2 начинает сливать, т.к. бит режима съедает мантиссу каждые ?16 против ?256.

defuz
08.08.2019 00:32В диапазоне от 1/16 до 16 лежит половина всех значений p32e2. Еще четверть лежит в диапазоне от 1/256 до 256.

defuz
07.08.2019 23:04Посчитал распределение для умножения и деления.
Умножение:

Деление:

Кажется тут позиты уделывают флоаты однозначно.
Pand5461
08.08.2019 00:29+1А что вы тут конкретно сравниваете?
Если вы берёте два позита, перемножаете их и сравниваете с "точным" результатом перемножения исходных позитов, — это не имеет смысла, т.к. даже в "точном" произведении значащих бит не больше, чем в исходных сомножителях.

defuz
08.08.2019 00:38Я сравниваю результат умножения двух позитов с умножением их рациональных представлений (натуральных дробей). Так что тут точность корректного результата не теряется никак.
На самом деле сведение к f64 дает неотлимый график:
(p1 * p2) as f64 / (p1 as f64 * p2 as f64)
Pand5461
08.08.2019 00:42+1Так это бессмысленно.
Вы берите сначала дроби, перемножайте как рациональные числа и сравнивайте результат с произведениями этих же дробей, округлённых в float и в posit.

defuz
08.08.2019 00:59То что вы предлагаете тоже бессмыслено в какой-то степени. При вычислениях большинство операций выполняются с аргументами которые были получены в результате других операций, то есть они уже и так были округлены до позитов/флоатов.
Эти графики в первую очередь демонстрируют как позиты или флоаты сохраняют точность гуляя по полю собстенных значений при выполнении операций. Тут важно не столько то как выполняется операция, как то какие значения нам доступны в поле чисел.
Вас же скорее интересует точность преобразования рациональных чисел во флоаты/позиты. Такой график тоже можно построить, но это про другое.
Pand5461
08.08.2019 01:31Ну посмотрите, что ли, разницу (ab)c — a(bc). Это же входит в категорию "гуляют по полю собственных значений"?

defuz
08.08.2019 01:59Держите. Только я посчитал (ab)c / a(bc), чтобы погрешности были нормализованы. Деление точное, без округлений, умножение – с округлениями.

Ожидаемо, график флоатов посередине улетает в бесконечность, потому что для случайных флоатов a*b*c в половине случаев приводит к underflow/overflow.
Вообще не потеряли точность флоаты в 35% случаев, позиты – в 67%.
Pand5461
08.08.2019 10:15+2В защиту флоатов я тут скажу, что без переполнения они таки гарантируют точность 2-23.
А дальше… В общем, Густафсону указывают на проблему: перемножение очень большого числа на очень маленькое вызывает потерю значащих цифр в произведении. Он этот аргумент просто игнорирует. А в физике такой юзкейс сплошь и рядом — тераваттный лазер с импульсом в наносекунду, тяга Saturn V поделить на массу Saturn V, произведение постоянной Планка на терагерцовую частоту, гравитационная постоянная на массу Земли, число Авогадро на постоянную Больцмана и т.д. Наиболее патологический для позитов случай будет (x * y) / y, где y — порядка 1025-30.
В лазерах сейчас, например, начали играться с такой штукой — как два импульса по мишени взаимодействуют между собой. И вполне могут бить сначала микросекунду мегаваттом, потом пикосекунду тераваттом. Произвольно менять единицы времени и мощности — ата-та, у нас же ещё есть плотность мишени, размер пятна, их тогда тоже придётся перемасштабировать. А если сложная симуляция, в которой подключается взаимодействие ЭМ поля с веществом — нужна ещё, как минимум, скорость света.

DrSmile
08.08.2019 12:54Эти графики в первую очередь демонстрируют как позиты или флоаты сохраняют точность гуляя по полю собстенных значений при выполнении операций.
Я тут подумал и понял, что это неверно. Эти графики показывают вносимую погрешность операций, никак не соотнося ее с погрешностью исходных операндов. Т. е. если исходная погрешность 10-7, то дополнительной погрешностью операции в районе 10-9 можно просто пренебречь.
На практике, при анализе накопления ошибок, вносимой погрешностью операции можно пренебречь почти всегда, по сравнению с погрешностью операндов, кроме случая денормалов для обычных флоатов и умножений/делений поситов. Наверное, надо строить графики относительной вносимой погрешности: отношения погрешности, вносимой операцией, к погрешности из-за дискретизации исходных операндов.
defuz
08.08.2019 16:08Эти графики показывают вносимую погрешность операций, никак не соотнося ее с погрешностью исходных операндов.
Согласен, я это и имел ввиду – как позиты сохраняют точность во время выполнения операций.
Я понял вашу мысль. Погрешность a + b не может быть ниже чем сумма погрешностей a и b. Но вот это мне не понятно:
надо строить графики относительной вносимой погрешности: отношения погрешности, вносимой операцией, к погрешности из-за дискретизации исходных операндов.
Что нам даст отношение этих погрешностей? Обе погрешности могут быть очень высоким и очень низким, а их отношение – одинаковым, хотя второй вариант очевидно предпочтительней. Пока мне приходит в голову брать максимальную погрешность из двух для каждого случая. Вроде бы это правильных подход, потому что каждая погрешность вносит свой вклад независимо относительно истинного значения, а не последовательно.
DrSmile
08.08.2019 16:37Что нам даст отношение этих погрешностей?
Ухудшение погрешности в результате операции. Погрешности операндов присутствуют до операции и про них есть отдельный график, интересно же узнать, насколько неточность операции увеличивает уже существующую погрешность.
В общем, такая относительная погрешность — это характеристика баланса точности до и после операции. Если такая погрешность много больше единицы, то это значит, что точность результата недостаточна, происходит потеря информации. Если много меньше — наоборот, точность результата излишняя, биты тратятся впустую.

akhalat
07.08.2019 12:57Линия позитов идет ниже линии флоатов для любого X.
таки на графике деления (второй в вашем сообщении), линия позитов выглядит выше в диапазоне 12~14 000
defuz
07.08.2019 14:43Таки да. Мы же с DrSmile обсуждали конкретный график, и я отвечал на вопрос что будет если его отмасштабировать.
То что линия позитов идет выше линии флоатов в том месте при делении говорит о том, что при делении флаты дают чуть больше точных результатов чем позиты. Но если результат неточен (а это большинство случаев), то позиты дают меньшую ошибку.

michael_vostrikov
06.08.2019 11:44Возможно, наибольшими возможностями posit будут обладать в области машинного обучения, где 16-битные числа можно использовать для обучения, а 8-битные – для проверки.
Мне кажется, в области машинного обучения лучше вообще использовать fixed-point значения. Там числа находятся недалеко от нуля и имеют значащие разряды с десятых долей, зачем там астрономические или микроскопические величины, где экспонента экономит биты.

defuz
06.08.2019 19:45В случае inference да, а вот в случае обучения приходится работать с float, причем приходится брать разрядность с большим запасом. Вот тут как раз posit могут помочь.

AVI-crak
06.08.2019 12:08Если это плавающая точка — то чем управляется разрядность целого и дробного числа?

defuz
06.08.2019 18:24Разрядность целого и дробного числа не управляется на прямую но зависит экспоненты, которая в свою очередь опредляется значением regime (количество последовательных нулей или единиц в начале битового представления).

Nomad1
06.08.2019 14:08Есть ли реализованная библиотека мат функций с таким представлением числа? Проводились ли тесты по скорости и точности?

defuz
06.08.2019 18:22+1SoftPosit – основная реализация. Очевидно что софтварная эмуляция posit медленее аппаратной реализации float. До массовой аппаратной поддержки еще не дошли, есть только единичные исследования. Если использовать Quire в аппаратной реализации, то интуитивно это должно быть быстрее и энергоэфективнее чем float. Если аппаратно реализовывать posit (что не очень разумно) – то float скорее всего будет выигрывать из-за отсутствия динамического сдвига между мантиссой и экспонентой. Исследования точности занимает сотню страниц в основном документе о Posit.

newpavlov
06.08.2019 14:22+2А теперь немного критики:
https://marc-b-reynolds.github.io/math/2019/02/06/Posit1.html
https://hal.inria.fr/hal-01959581v4
Из последней ссылки:
When posits are better than floats of the same size, they provide one or two extra digits of accuracy. When they are worse than floats, the degradation of accuracy can be arbitrarily large. This simple observation should prevent us from rushing to replace all the floats with posits.

defuz
06.08.2019 19:05Вообще такого рода сравнение изначально предполагает равномерное распределение используемых рациональных чисел, и все они вносят равнозначный вклад в качество вычисления, что не верно примерно всегда. Как минимум потому что в результате первого же вычисления мы не можем получить произвольное рациональное число, а лишь одно из тех что доступно в нашем представлении. А значит в следующем вычислении уже будут использоваться не все рациональные числа, и так далее. Точность стоит рассматривать в первую очередь для понимания как работает система исчисления, но использовать точечные результаты для сравнения двух систем не корректно.
Так же следует учитывать что posit справляется со значительным количеством случаев, где float не выдает адекватного результата вообще. Это стоит учитывать при сравнении. Но всегда можно найти такой пример, в котором любая разумная система исчисления будет лучше другой. В этом смысле действительно не корректно говорить что posit лучше чем float.

vics001
06.08.2019 15:49+4По документу: идея интересная, но кажется довольно сырая. В смысле пару идей точно хороших, особенно супер экспонента и динамически фиксированная точность, но пару идей не хватает. В основном людей раздражает точность сложений и умножений в float и это надо решать. С другой стороны float достаточно мал, это всего 32 бита.
Главная проблема: точность posit хуже на сложении маленьких чисел.
Posit

vics001
06.08.2019 15:57Мне кажется идеальный exponential это функция 4х параметров :( 1-й значимая часть, 2-я множитель (экспонента или суперэкспонента), 3-я числитель и 4-я знаменатель. Но это аж 4 числа и их еще надо разделять как-то. x = a * b + c / d или x = (a * b + c) / d

defuz
06.08.2019 18:16Идея не сырая, ее просто не представили здесь в полной мере. Есть еще Quire – логическое развитие Posit, которое как раз позволяет не терять точность при сложении и умножении. Ключевая идея в том, что формат Posit используется для хранения чисел в памяти, в то время как Quire – для проведения вычислений в регистрах.
Таким образом с одной стороны экономится память и затратность обращения к ней (в большинстве случаев можно использовать posit меньшей размерности чем float), с другой – увеличивается точность за счет использования аккамуляторов не приводящих к потере точности.
khim
06.08.2019 19:33Таким образом с одной стороны экономится память и затратность обращения к ней (в большинстве случаев можно использовать posit меньшей размерности чем float), с другой – увеличивается точность за счет использования аккамуляторов не приводящих к потере точности.
Это уже пробовали. 8087 называется. Сколько глюков это порождает — и не сосчитать…
defuz
06.08.2019 19:42А можно подробнее? В таких случаях важно разобраться что было проблемой – идея или реализация.

khim
06.08.2019 20:26+2Проблемой было то, что люди не программируют программы на ассемблере, а подавляющее большинство языков программирования «не умеют» в два представления. Соответственно в зависимости от того что, куда и когда компилятор решит посчитать на регистрах (в extended точности), а когда что-то попадёт в память результаты получались разные. Причём сильно разные.
В результате, например, программа, рассчитывающая сворачиваемость белков — теряли или дублировала варианты при запуске параллельно на нескольких машинах.
Появление x86-64 и переход на SSE2, где все числа всегда одного размера — это было просто «щастя» какое-то!
То есть выигрыш от более точных вычислений никого не волновал, но вот неустойчивость результата (на одинаковых входных данных получаем разные выходные) — напрягала очень сильно.
firk
06.08.2019 23:09Это дезинформация. У х87 есть специальная настройка (поле PC в регистре управления) для понижения точности регистровых вычислений хоть до double хоть до single. Сделано как раз для того чтобы было проще делать детерминированные алгоритмы вычислений.
То что ряд компиляторов не умеет этим пользоваться — проблема компиляторов а не проца.
Появление x86-64 и переход на SSE2, где все числа всегда одного размера — это было просто «щастя» какое-то!
Соответственно, это тут тоже ни при чём.

khim
07.08.2019 11:52То что ряд компиляторов не умеет этим пользоваться — проблема компиляторов а не проца.
Если подавляющее большинство компиляторов чем-то не умеют пользоваться — это становится проблемами проца.
Беда в том, что достаточно быстро менять эти настройки можно только на оригинальном 8087. А на каким-нибудь Pentium'е это весь пайплайн сбивает. Потому и не дёргает их никто перед каждым вычислением.
Да и не было это так задумано. Идея была, что программисты будут всё рачками писать — отсюда и стековая архитектура и прочее… А они — не захотели, редиски. И сейчас не хотят.
Соотвественно, если рассматривать реальные программы, а не чьи-то влажные мечты, то SSE решил эту проблему.Появление x86-64 и переход на SSE2, где все числа всегда одного размера — это было просто «щастя» какое-то!
Соответственно, это тут тоже ни при чём.
firk
08.08.2019 12:10А на каким-нибудь Pentium'е это весь пайплайн сбивает. Потому и не дёргает их никто перед каждым вычислением.
Перед каждым и не надо, надо в начале работы программы и иметь соглашение что библиотеки эту настройку не ломают — то есть если меняют (а обычно им незачем) то на выходе ставят обратно, а конвеер там всё равно сбивается из-за передачи управления.
На всякий случай также упомяну, что с точки зрения си будет корректным проведение всех вычислений с точностью double. То есть разница между
float a,b,c;
a = a*b; a = a*c;и
float a,b,c;
a = a*b*c;(то, что во втором случае будет точнее и возможно другой результат) заложена в стандарте языка и х87 тут опять ни при чём.
Да и не было это так задумано.
Эта настройка была сделана именно для поддержки языков в которых подразумевается не максимальная точность вычислений.

khim
08.08.2019 13:22Перед каждым и не надо, надо в начале работы программы и иметь соглашение что библиотеки эту настройку не ломают — то есть если меняют (а обычно им незачем) то на выходе ставят обратно, а конвеер там всё равно сбивается из-за передачи управления.
Как вы это себе представляете, интересно? Во многих программах есть и 32-битные float и 64-битные double. Вы ж не можете в 8087 включить сразу два режима.
На всякий случай также упомяну, что с точки зрения си будет корректным проведение всех вычислений с точностью double.
Только в режиме без оптимизаций. Если же вы перемножаете два числа и кладёте их в третье — в этот момент дожно произойти преобразование во float.
(то, что во втором случае будет точнее и возможно другой результат) заложена в стандарте языка и х87 тут опять ни при чём.
Стандарт это разрешает, но не требует. И большинство процессоров всё считают в одинарной точности.
Эта настройка была сделана именно для поддержки языков в которых подразумевается не максимальная точность вычислений.
Эта настройка была сделана, когда 8086 считался временной заглушкой до прихода iAPX 423. На 8087 (оригинальном) смена режимов была дёшева, а о XXI веке никто не думал…
8087 — это весьма продуманный дизайн для тех возможностей, которые были у его создателей. Но когда от него удалось отказаться в пользу SSE — разработчики «вздохнули с облегчением»…

DistortNeo
07.08.2019 01:10+1Появление x86-64 и переход на SSE2, где все числа всегда одного размера — это было просто «щастя» какое-то!
До появления операции FMA, в которой результаты промежуточных вычислений не огрубляются. Захотел компилятор оптимизировать код и использовать новую инструкцию — получите другой результат.

khim
07.08.2019 11:55Да, есть такое дело. Однако тут речь идёт об одном бите, фактически, и двух операциях. В 8087 с «повышенной точностью» могли исполняться десятки операций.

defuz
07.08.2019 03:10точность posit хуже на сложении маленьких чисел.
Преведенные вами графики построены по двум разным системам исчестления, так что одинаковые координаты не соответствуют одним и тем же числам.
Если под маленькими числами подразумевать числа со значением экспоненты близкой к нулю (скажем от 1e-10 до 1e10) то позиты как раз таки предлагают гораздо более высокую точность в этом диапазоне.

yleo
06.08.2019 19:25Заголовок статьи совсем не совпадает со смыслом.
Никакого "избавления" нет, только альтернативное представление для хранения, которое лучше в одних случаях и хуже в других.

red_andr
06.08.2019 20:46Если уполовинить количество битов, можно не только уменьшить объёмы кэша, памяти и хранилища для этих чисел, но и серьёзно уменьшить ширину канала, необходимого для передачи их на процессор и обратно. Это главная причина, по которой арифметика на базе posit, по его мнению, даст от двойного до четверного ускорения расчётов по сравнению с числами с плавающей запятой от IEEE.
Однако эта арифметика сама по себе более медленная. Причём неизвестно насколько, так как нет её реализации в железе. Скажем, если они будет в 5 раз медленнее, то толку от такого перехода? И, честно говоря, я сомневаюсь, что на самом деле, скажем, Float64 медленнее Float32 настолько. В своё время тестировал свои численные алгоритмы на разную точность и падение производительности было процентов 20, точно не больше 50. А хранить данные можно в меньшей точности, с сжатием, с преобразованиями в другой формат и так далее.
khim
06.08.2019 22:29+2И, честно говоря, я сомневаюсь, что на самом деле, скажем, Float64 медленнее Float32 настолько.
Двухкратная разница как минимум (Tesla V100), а может быть и разница раз в так в 30 (Quadro RTX 8000: 16312 GFLOPS vs 509.8 GFLOPS). То что вы получали разницу в 20% обозначает просто что плавучка не была «бутылочным горлышком» ваших алгоритмов. Может они в память упирались или просто там было много уровней индирекции.
red_andr
06.08.2019 23:40Действительно, «плавучка» в реальных задачах редко бывает «бутылочным горлышком». Даже в вылизанном и чистом Linpack максимальная производительность раза в два ниже пиковой. Я, само собой, тестировал реальные задачи на обычном процессоре.
Насчёт же огромной разницы у ускорителей на 32- и 64-битной точности. Конкретно на RTX 8000 стоит ровно в 32 раза меньше F64 блоков чем F32. У V100, как можете догадаться, первых блоков всего в два раза меньше. Поэтому разница не удивительна, так как фактически вычисления той и другой точности производятся на разных устройствах. Так что, давайте таки сравнивать одно и тоже, например CPU. Или Xeon Phi.
khim
07.08.2019 12:02+1Или Xeon Phi.
Xeon Phi используется на горсточке суперкомпьютеров. А вот GPU — на большинстве. При этом эти же рассчёты, зачастую, люди делают на своих домашних GPU, если нет доступа к суперкомпьютерам.
red_andr
07.08.2019 20:34Я в курсе, но не это было в моём комментарии главным. Мой посыл был в том, что нельзя утверждать, что вычисления с двойной точностью в 30 раз медленнее, чем с одинарной, используя в качестве обоснования характеристики устройства, в котором производитель реализовал намного меньше блоков для вычислений двойной точности, как он сам утверждает, чисто для совместимости. В специализированных ускорителях, например V100 или Xeon Phi, и обычных процессорах разница, как правило, всего в два раза. Причём подчеркну, что разница между теоретическими производительностями, реально она меньше.

Arris
06.08.2019 21:38+1Тот случай, когда оригинал читать легче, чем этот, с позволения сказать «перевод»

Taras-proger
07.08.2019 20:08Вот только даже равная со средним числом погрешность в одном маленьком числе делает бессмысленными и его, и все средние и большие числа.


kasyachitche
Вот и первая ласточка значительного качественного роста производительности процессоров. Возможно, еще пара технологий и новые техпроцессы вовсе перестанут окупаться.
khim
Программисты всегда найдут способ выпустить весь пар в свисток.
aakolov
Больше фреймов в видеоиграх! Еще 33 прослойки в фреймворках! Ещё больше круглых уголков в интерфейсах! Ещё 100500 гигабайт джаваскриптов на каждой вебстранице!
Mirn
даёшь на каждую операцию с таким типом данных декомпрессор в дабл или long double и обратно!
всё ради «быстродействия», «совместимости» или продаж нового оборудования!
А если честно то такое реализовать на FPGA, ASIC и новых чипах будет ещё сложнее чем флоаты (которые уже реализованы в аппаратных блоках в старших версиях). И самое худшее — приведёт к сильному удлинению конвеера CPU/GPU, ещё к более сложному управляющему устройству, к ещё более сложным алгоритмам предсказаний переходов инструкций и будущих данных и к ещё большим продажам новых IP ядер несовместимых с старыми. (может быть в этом и цель? как на авто: сделать «эко» режим и объявить остальное нормально ездящее вне закона? тем самым создав иллюзию повышения продаж)