По материалам статьи Julien Clinton Sprott. Dynamical models of love. Nonlinear Dynamics Psychology and Life Sciences, August 2004.

Я алгеброй гармонию поверил…
Теория мой друг суха, но древо жизни вечно зеленеет…

Кто только не бился об эту «проблему»…. Ее разбирали в древнегреческих трагедиях, великий Шекспир рассказал нам историю Ромео и Джульетты, Анджей Вайда разобрал ее с обеих сторон в «Анатомии любви». Но люди так и не докопались до истины, пока за решение не взялись ученые. Правда, у психологов не все выглядит вполне убедительно. Они порой сами уже после собственного развода начинают анализировать историю своей ушедшей любви. Ну и писать книги, которые иногда идут нарасхват. Их же пишут специалисты! Что тут скажешь? Почти ничего личного – только бизнес…

И вот наконец, не поэты с писателями и психологами взяли любовь за горло. Математика – царица наук. Способна ли она справиться с вечной проблемой? Выходят книги, например, Джона Готмана «Математика брака», и других авторов. Развитие романтических отношений математики рассматривают как динамический процесс…

И начинается все, как и положено, с определений. Как выявить любовь качественно и количественно? Исследователи классифицируют проблему по видам: любовная связь, страсть, верность. При этом каждому виду присущ сложный набор чувств. А ведь кроме любви к другому человеку существует любовь к себе, к жизни, к человечеству…

При этом противоположностью любви – в математической модели — не может быть ненависть, так как оба эти чувства могут сосуществовать одновременно. Например, кому-то могут нравиться одни проявления у партнера, но быть противными другие. Поэтому нереалистично предполагать, что на любовь индивидуума влияют только его собственные чувства, а чувства другого партнера не зависят от прочих влияний, и что параметры, характеризующие взаимодействие двоих людей, остаются неизменными и таким образом исключают возможность обучения и адаптации.

Сложность даже в минимальной ограниченной модели резко возрастает при введении в уравнения нелинейности и/или наличии трех или более переменных.

* Примеч.переводчика. На мой взгляд, подобные исследования способны еще и оживить саму математику, привлечь к ней внимание обычно отстраненной от этой абстрактной науки публики.

Простая линейная модель

Историю любви Ромео и Джульетты во времени (t) можно представить с помощью функций* R(t) – любовь Ромео к Джульетте и J(t) — любовь Джульетты к Ромео.

Тогда простая линейная модель их взаимоотношений выразится уравнениями (1)



a и b – параметры романтического стиля Ромео
c и d — параметры стиля Джульетты
a – характеризует, насколько Ромео охвачен своими собственными чувствами
b – насколько Ромео охвачен чувствами Джульетты

В одной из статей (Готман с соавторами, 2002) используется термин «поведенческая инерция» для первого и «функция влияния» для второго параметра. Хотя при a=0 инерция становится наибольшей. Динамическая модель при таких условиях является двумерной и управляемой по начальным условиям и четырем параметрам, которые могут быть положительными или отрицательными.

Простая линейная модель была предложена в работе Ринальди, 1998a. При этом к каждой из производных добавляется свободный член с целью учета притягательности (или антипатии при отрицательном значении), которую каждый из партнеров проявляет к другому при отсутствии прочих чувств. Подобная модель является более реалистичной, поскольку допускает нарастание чувств от состояния безразличия и обеспечивает равновесие, не характеризующееся посредством полной апатии. Все это описывается так только при вводе двух дополнительных параметров. В то время как состояние неапатичного равновесия может быть очень важным для рассматриваемых личностей, это не изменяет динамику иначе, чем посредством перемещения пространства состояния RJ.

Романтические стили

Ромео может проявлять один из четырех романтических стилей в зависимости от знаков a и b, с обозначениями, данными автором работы (Strogatz, 1994) и его студентами:

1. Страстный возжелатель: a > 0, b > 0 (Ромео охвачен собственными чувствами и чувствами Джульетты.)
2. Самовлюбленный тип: a > 0, b < 0 (Ромео больше охвачен собственными чувствами, он отстраняется от чувств Джульетты.)
3. Осторожный (или надежный любовник): a < 0, b > 0 (Ромео отдаляется от собственных чувств, но он охвачен чувствами Джульетты.)
4. Отшельник: a < 0, b < 0 (Ромео отстраняется от собственных чувств и чувств Джульетты.)

Так как для Джульетты также возможно проявление четырех стилей поведения, то всего существует 16 вероятных сочетаний пар, каждая с собственной динамикой, хотя половина из них соответствует перестановке R и J.

Уравнения (1) определяют единственную точку равновесия при R = J = 0, что соответствует обоюдно безразличным отношениям, или так называемому «плато любви» (в модели Rinaldi, 1988 ), с описанием поведения посредством собственных значений (2)




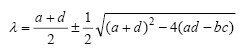
Фокус Разветвление Седло
Рис. 1. Динамическая ситуация вблизи точки равновесия в двумерном пространстве, согласно уравнению 1.

Треугольник любви

Более математически богатая модель получается при добавлении к простой модели третьей личности, в частности потому, что возможно возникновение союзов, в которые две личности могут объединяться против третьей. Допустим, у Ромео есть другая любовница, Женевьева, хотя третьим рассматриваемым лицом может быть ребенок или другой родственник. Пространство состояний становится при этом уже скорее шестимерным, чем двумерным, поскольку каждый из троих имеет чувства к двум другим, и при этом возникает двенадцать параметров, если каждый может принимать различные стили по отношению к другим, даже в случае, если игнорируется природное влечение, (рассматриваемое Rinaldi, 1998a ).

В простейшем случае Джульетта и Женевьева могут не знать о существовании друг друга, а Ромео может проявлять одинаковый романтический стиль в отношении обеих. Результирующая четырехмерная система преобразуется тогда в две разделенные двумерные системы, до тех пор, пока на чувства Ромео к Джульетте каким-то образом не окажут воздействия чувства Женевьевы к нему, и то же аналогично в отношении Женевьевы.

Нелинейные эффекты

Существует бесконечное множество способов для ввода нелинейных эффектов. Представим, что Ромео положительно отвечает на любовь Джульетты, но при чрезмерном проявление ее любви он чувствует себя как бы придушенным и проявляет при этом неблагоприятную реакцию. И наоборот, если Джульетта выказывает достаточно неприязни, Ромео может постараться стать приятным для нее.

При этом возможно заменить bJ в уравнении 1 логистической функцией bJ(1 – |J|), соответствующей измерению J в единицах из условия что J = 1 соответствует значению, при котором ее любовь становится приводящей к обратным результатам. Качественно подобные результаты следуют из функции bJ(1 – J2), которая является случаем, рассматриваемым Rinaldi (1998b) для модели платонической любви итальянского поэта 14-го века Франческо Петрарки к прекрасной Лауре, связанной узами брака. Допуская то же самое для Джульетты, получим:
(4)



Имеется 4 равновесных состояния, включая одно в начале координат. На рис.3 показан устойчивый фокус, при котором Джульетта. как «страстный возжелатель» (c = d = 1) увлекает «отшельника» Ромео (a = b = –2) к состоянию взаимной любви при R = J = 2. Подобная модель для осторожных (надежных) любовников с сигмоидальной нелинейностью также приводит к стабильному равновесию (Rinaldi и Gragnani 1998 ). Уравнения 4 очевидно не допускают предельных циклов, и хаос не возникает, пока система является двумерной.


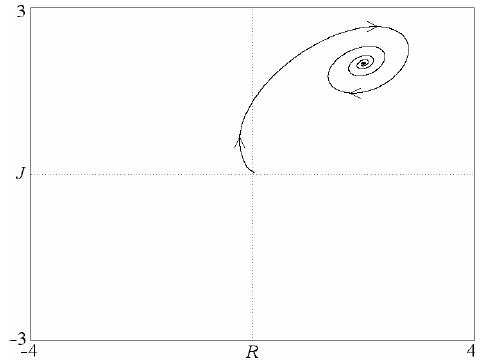
Рис. 3. Одно из решений для нелинейной модели согласно уравнению 4.

Возможно приложение нелинейных эффектов и к треугольникам любви.

Послесловие

Некоторые из линейных динамических моделей любви проявляют удивительно сложную динамику, при этом многое в них кажется похожим на известный опыт в отношениях. При наличии трех или более переменных и введении даже простейших нелинейных эффектов возможно возникновение хаоса. Интересное расширение модели можно себе представить при рассмотрении группы взаимодействующих личностей, например, для случаев большой семьи или коммуны. Подобные модели, конечно, являются очень упрощенными, поскольку любовь в них учитывается как простая скалярная переменная, а реакции личностей в отношении к собственной любви и любви к ним других личностей являются последовательными и механистичными, вне учета факторов внешнего влияния.

P.S. Любовь и без математики проживет, а вот математика вызывает любовь к себе людей, ценящих истинную гармонию.

Литература:
Julien Clinton Sprott. Dynamical models of love. Nonlinear Dynamics Psychology and Life Sciences • August 2004

Rinaldi, S. (1998a). Love dynamics: the case of linear couples. Applied Mathematics and Computation, 95, 181-192.
Rinaldi, S. & Gragnani, A. (1998). Love dynamics between secure individuals: A modeling approach. Nonlinear Dynamics, Psychology, and Life Sciences, 2, 283-301.
Rinaldi, S. (1998b). Laura and Petrarch: An intriguing case of cyclical love dynamics. SIAM Journal on Applied Mathematics, 58, 1205-1221