В этом посте мы рассмотрим этап работы с вершинами. То есть нам придётся снова достать учебники по математике и вспомнить линейную алгебру, матрицы и тригонометрию. Ура!

Мы выясним, как преобразуются 3D-модели и учитываются источники освещения. Также мы подробно объясним разницу между вершинными и геометрическими шейдерами, и вы узнаете, на каком этапе находится место для тесселяции. Чтобы облегчить понимание, мы используем схемы и примеры кода, демонстрирующие, как в игре выполняются вычисления и обрабатываются значения.

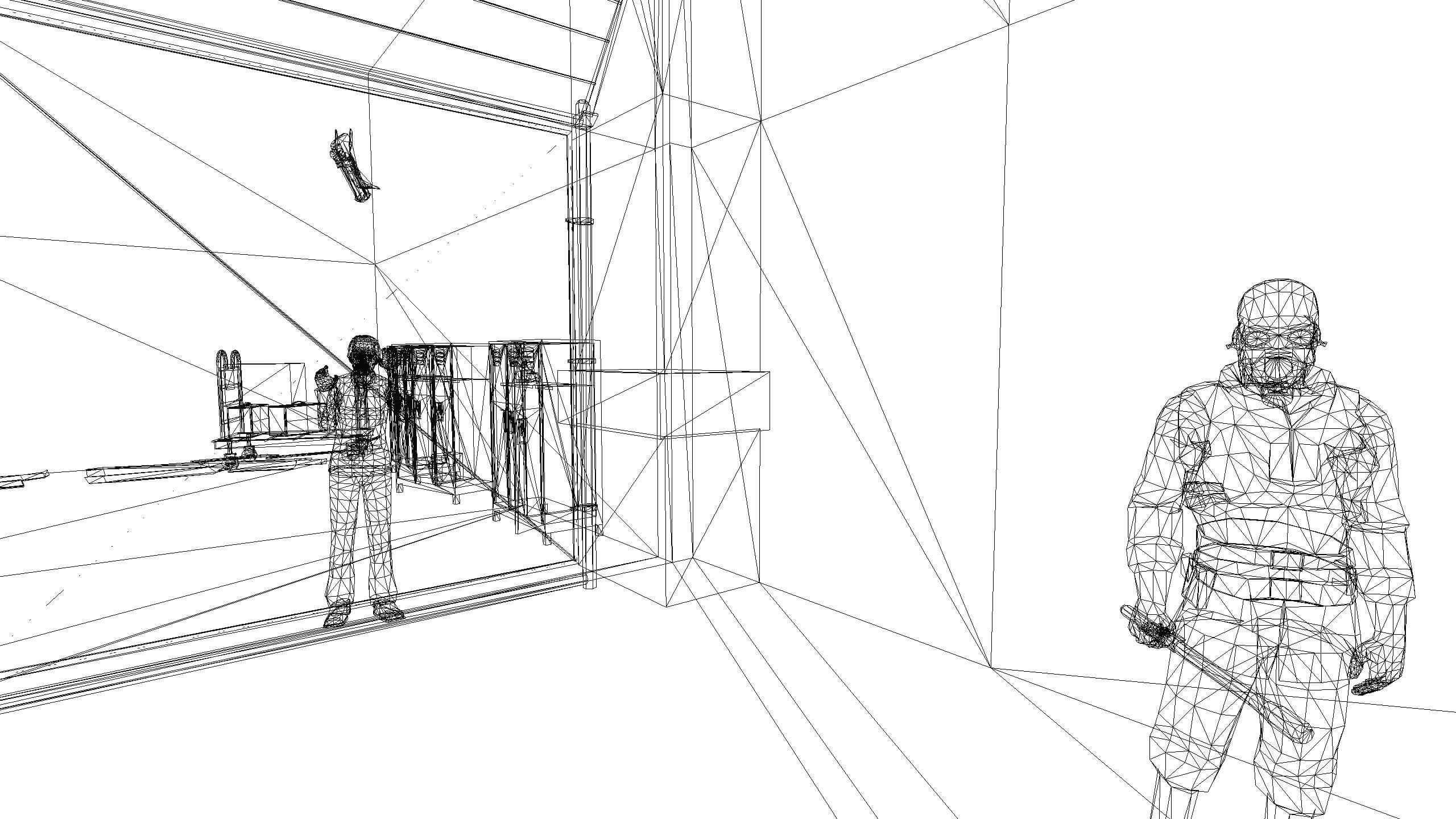
На скриншоте в начале поста показана игра GTA V в каркасном (wireframe) режиме отображения. Сравните её с намного менее сложным каркасным отображением Half-Life 2. Изображения созданы thalixte при помощи ReShade.

Что такое точка?

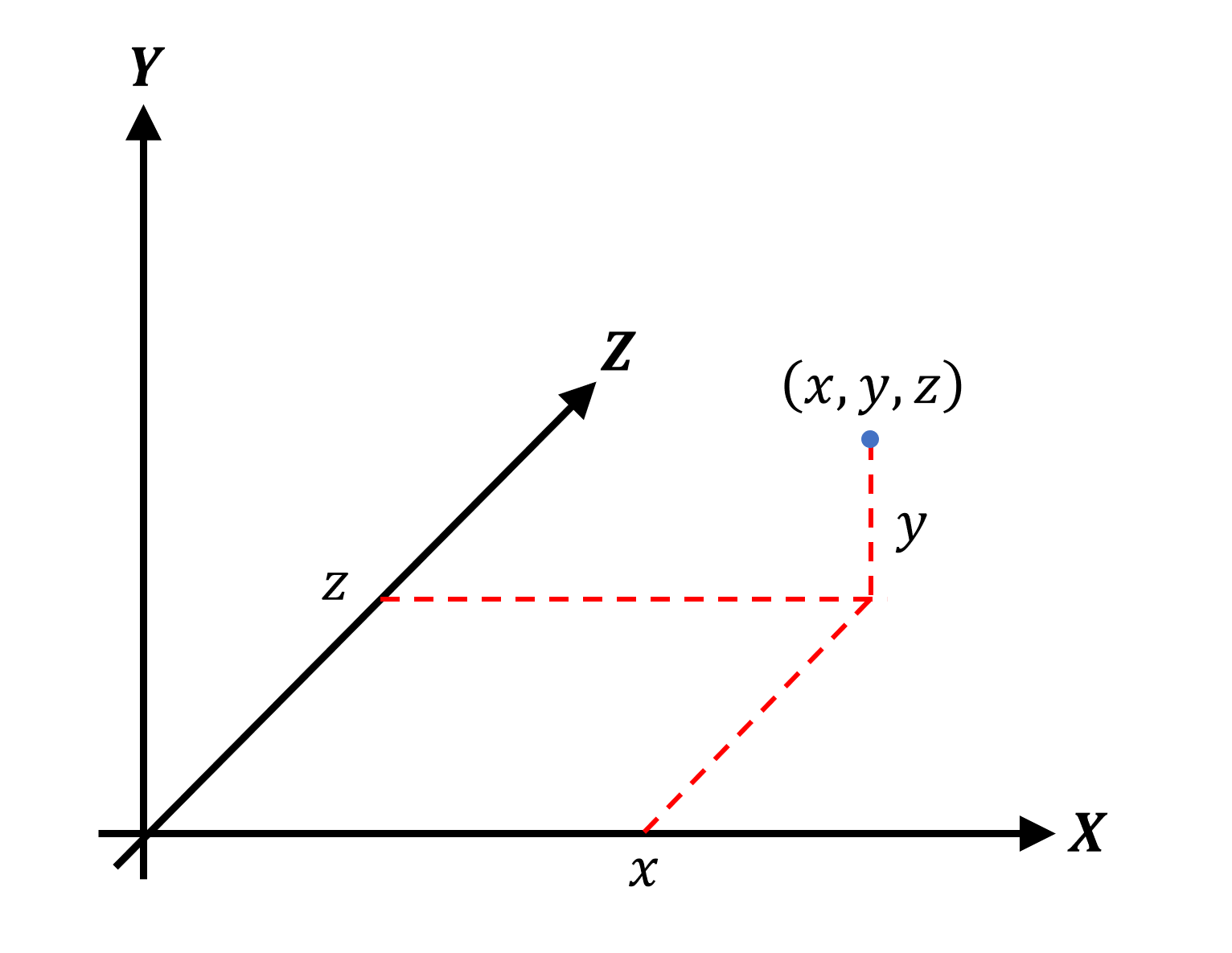
В мире математики точка — это просто место в геометрическом пространстве. Нет ничего меньше точки, она не имеет размера, поэтому точки можно использовать для точного задания местоположения начала и конца таких объектов, как отрезки прямых, плоскости и объёмы.

Для 3D-графики такая информация критически важна, от неё зависит внешний вид всего, потому что все объекты отображаются как наборы отрезков прямых, плоскостей и т.п. На изображении ниже показан скриншот из игры Bethesda 2015 года Fallout 4:


Возможно, вам будет непросто увидеть, что это всего лишь огромная куча точек и линий, поэтому мы покажем, как та же сцена выглядит в режиме wireframe. В таком режиме движок 3D-рендеринга пропускает текстуры и эффекты, выполняемые на этапе пикселей, и отрисовывает только разноцветные линии, соединяющие точки.


Теперь всё выглядит совершенно иначе, но мы видим, как все линии объединяются, образуя различные объекты, окружения и фон. Некоторые состоят всего лишь из десятков линий, например, камни на переднем плане, другие же содержат столько линий, что выглядят сплошными.

Каждая точка в начале и конце каждой линии обработана выполнением целой кучи вычислений. Некоторые вычисления очень просты и быстры, другие намного сложнее. Обрабатывая точки группами, особенно в виде треугольников, можно добиться значительного роста производительности, поэтому давайте внимательнее приглядимся к ним.

Что же нужно для треугольника?

Название треугольник даёт нам понять, что фигура имеет три внутренних угла; для этого ей нужны три угловых точки и три соединяющих их отрезка. Правильно называть угловую точку вершиной (vertex) (во множественном числе — vertices); каждая вершина задаётся точкой. Так как мы находимся в трёхмерном геометрическом мире, то для точек используется декартова система координат. Обычно координаты записываются в виде трёх значений, например, (1, 8, -3), или обобщённо (x, y, z).


Далее мы можем добавить ещё две вершины, чтобы образовать треугольник:


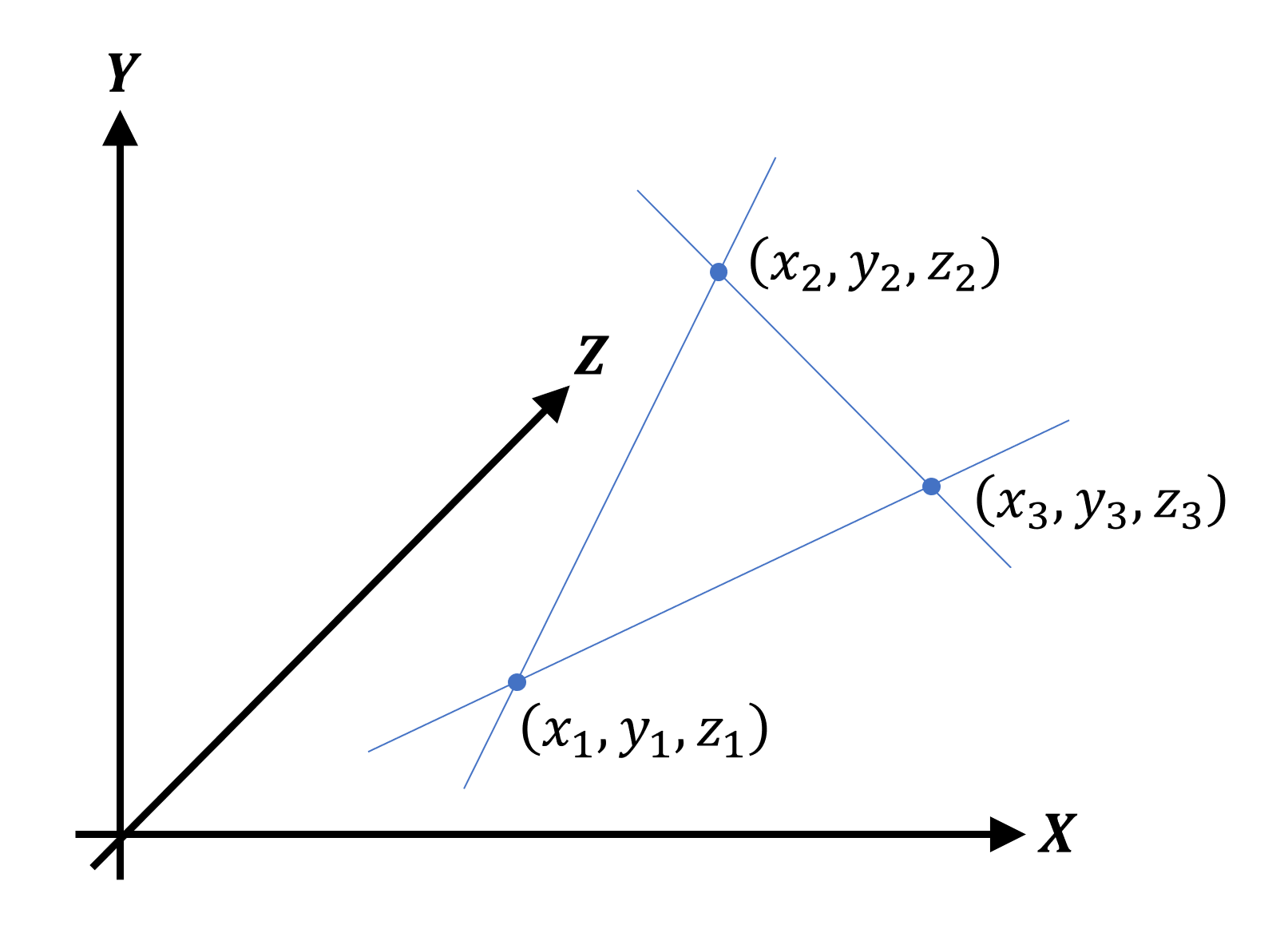
Учтите, что показанные линии не обязательны — мы можем задать точки и сказать системе, что эти три вершины образуют треугольник. Все данные вершин хранятся в непрерывном блоке памяти, который называется буфером вершин (vertex buffer); информация об образуемой ими фигуре или закодирована непосредственно в программе рендеринга, или хранится в ещё одном блоке памяти, называемом буфером индексов (index buffer).

Если информация закодирована в программе рендеринга, то различные фигуры, которые могут образованы вершинами, называются примитивами. Direct3D предлагает использовать для них список (list), полосы (strips) и «вееры» (fans) в форме точек, линий и треугольников. При правильном использовании полосы треугольников используют вершины более чем для одного треугольника, что позволяет повысить производительность. В показанном ниже примере мы видим, что для создания соединённых вместе двух треугольников нужно всего четыре вершины — если они разделены, то нам понадобится шесть вершин.


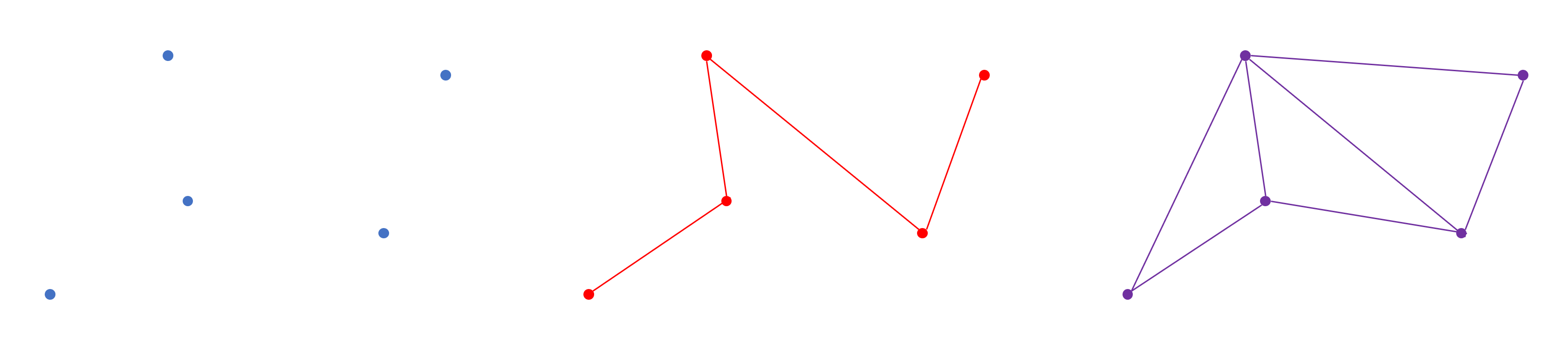
Слева направо: список точек, список линий и полоса треугольников

Если нам нужно обрабатывать больший набор вершин, например, в модели игрового NPC, то лучше использовать объект под названием меш (mesh) — ещё один блок памяти, но состоящий из нескольких буферов (вершин, индексов и т.д.) и ресурсов текстур модели. В онлайн-документации Microsoft есть краткое объяснение того, как использовать эти буферы.

Пока давайте сосредоточимся на том, что происходит с этими вершинами в 3D-игре при рендеринге каждого нового кадра. Если вкратце, то с ними выполняется одна из двух операций:

• Вершина перемещается в новую позицию
• Меняется цвет вершины

Готовы к математике? Отлично, потому что она нам и понадобится.

На сцене появляется вектор

Представьте, что у вас на экране есть треугольник и вы нажимаете клавишу, чтобы переместить его влево. Естественно, мы ожидаем, что числа (x, y, z) каждой вершины будут соответствующим образом меняться; так и происходит, однако довольно неожиданно выглядит способ реализации изменений. Вместо простого изменения координат подавляющее большинство систем рендеринга 3D-графики использует особый математический инструмент: мы имеем в виду векторы.

Вектор можно представить как стрелку, направленную в определённую точку пространства и имеющую нужную длину. Вершины обычно задаются при помощи векторов на основе декартовых координат:


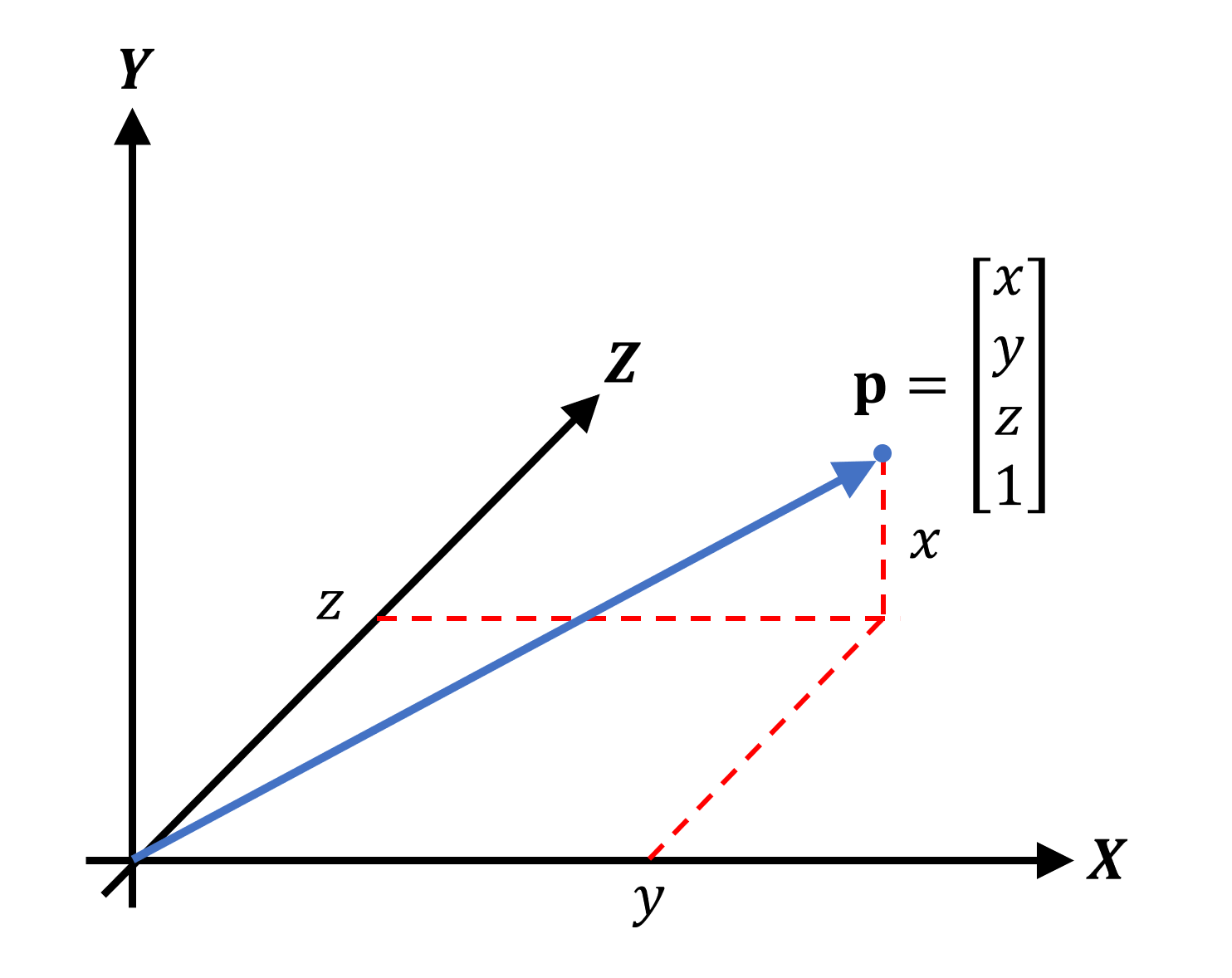
Заметьте, что синяя стрелка начинается в одном месте (в данном случае это точка начала координат (origin)) и растягивается до вершины. Для задания вектора мы использовали запись в столбец, но вполне можно применять и запись в строку. Вы могли заметить, что есть ещё одно, четвёртое, значение, обычно называемое w-компонентом. Оно используется для того, чтобы показать, что обозначает вектор: позицию точки (вектор позиции) или общее направление (вектор направления). В случае вектора направления это будет выглядеть следующим образом:


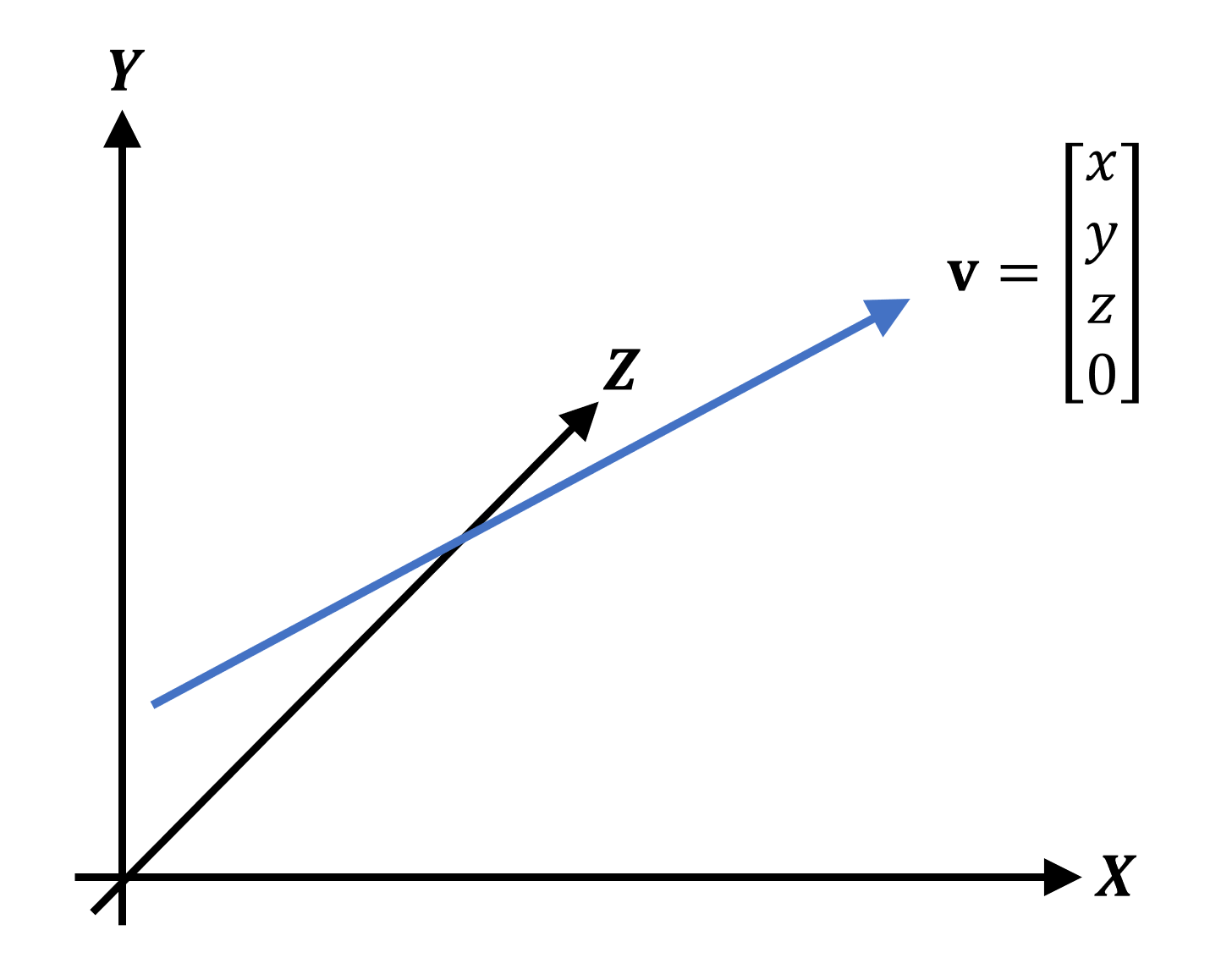
Этот вектор указывает в том же направлении и имеет ту же длину, что и предыдущий вектор позиции, то есть значения (x, y, z) будут такими же; однако w-компонент равен не 1, а нулю. Применение векторов направлений мы объясним позже, а пока запомните тот факт, что все вершины в 3D-сцене будут описываться таким образом. Почему? Потому что в таком формате гораздо проще их перемещать.

Математика, математика, и ещё раз математика

Вспомним, что у нас есть простой треугольник и мы хотим переместить его влево. Каждая вершина описывается вектором позиции, поэтому «математика перемещения» (называемая преобразованиями) должна работать с этими векторами. Появляется новый инструмент: матрицы (matrices) (matrix в единственном числе). Это массив значений, записанный в формате, похожем на электронную таблицу Excel, со строками и столбцами.

Для каждого типа преобразований существует соответствующая матрица, и для преобразования достаточно просто перемножить матрицу преобразования и вектор позиции. Мы не будем вдаваться в подробности того, как и почему это происходит, а просто посмотрим, как это выглядит.

Перемещение вершины в 3D-пространстве называется переносом (translation) и для него требуется следующий расчёт:


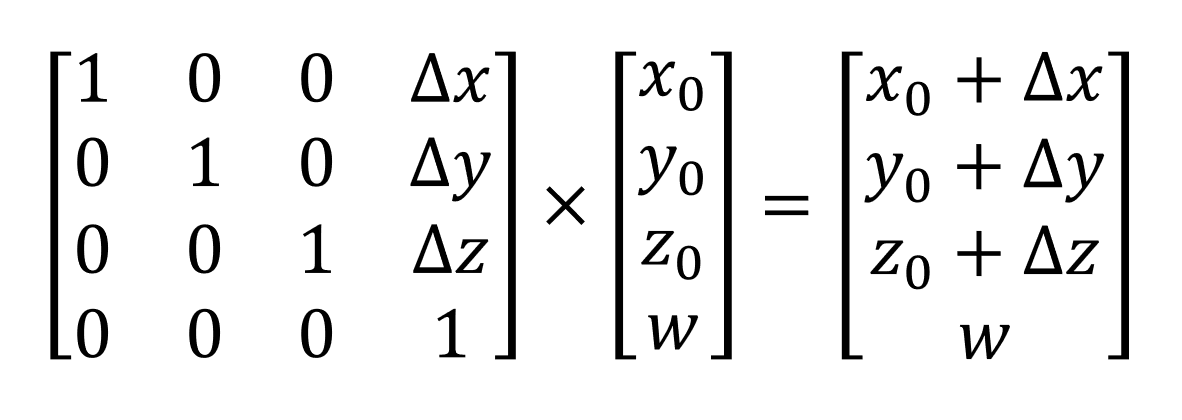
Значения x₀, и т.д. представляют исходные координаты вектора; значения delta-x представляют величину, на которую нужно переместить вершину. Перемножение матрицы и вектора приводит к тому, что они просто суммируются (заметьте, что w-компонент остаётся неизменным, чтобы готовый ответ по-прежнему оставался вектором позиции).

Кроме перемещения нам также может понадобиться поворачивать треугольник или изменять его масштаб — для этих операций тоже существуют преобразования.


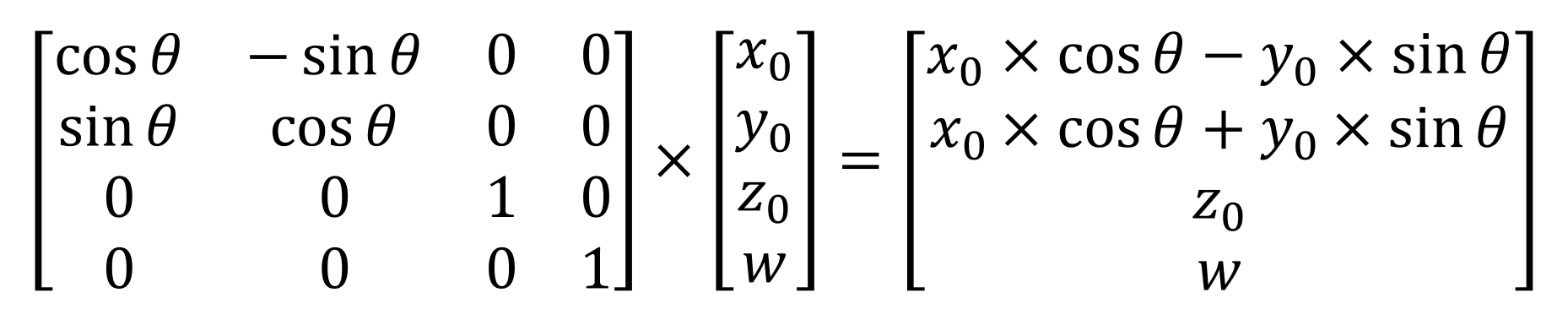
Это преобразование поворачивает вершину вокруг оси z в плоскости XY


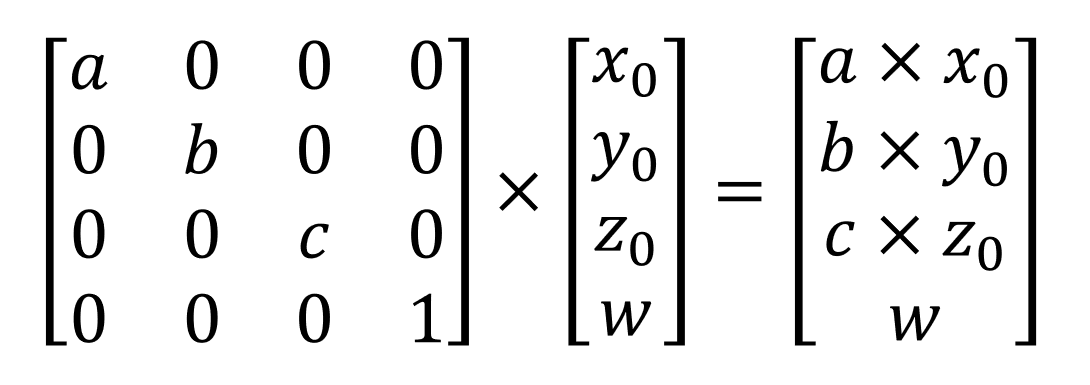
А это используется, если нужно изменить масштаб фигуры

Мы можем воспользоваться графическим инструментом на основе WebGL с сайта Real-Time Rendering, чтобы визуализировать эти вычисления для всей фигуры. Давайте начнём с прямоугольного параллелепипеда в стандартной позиции:


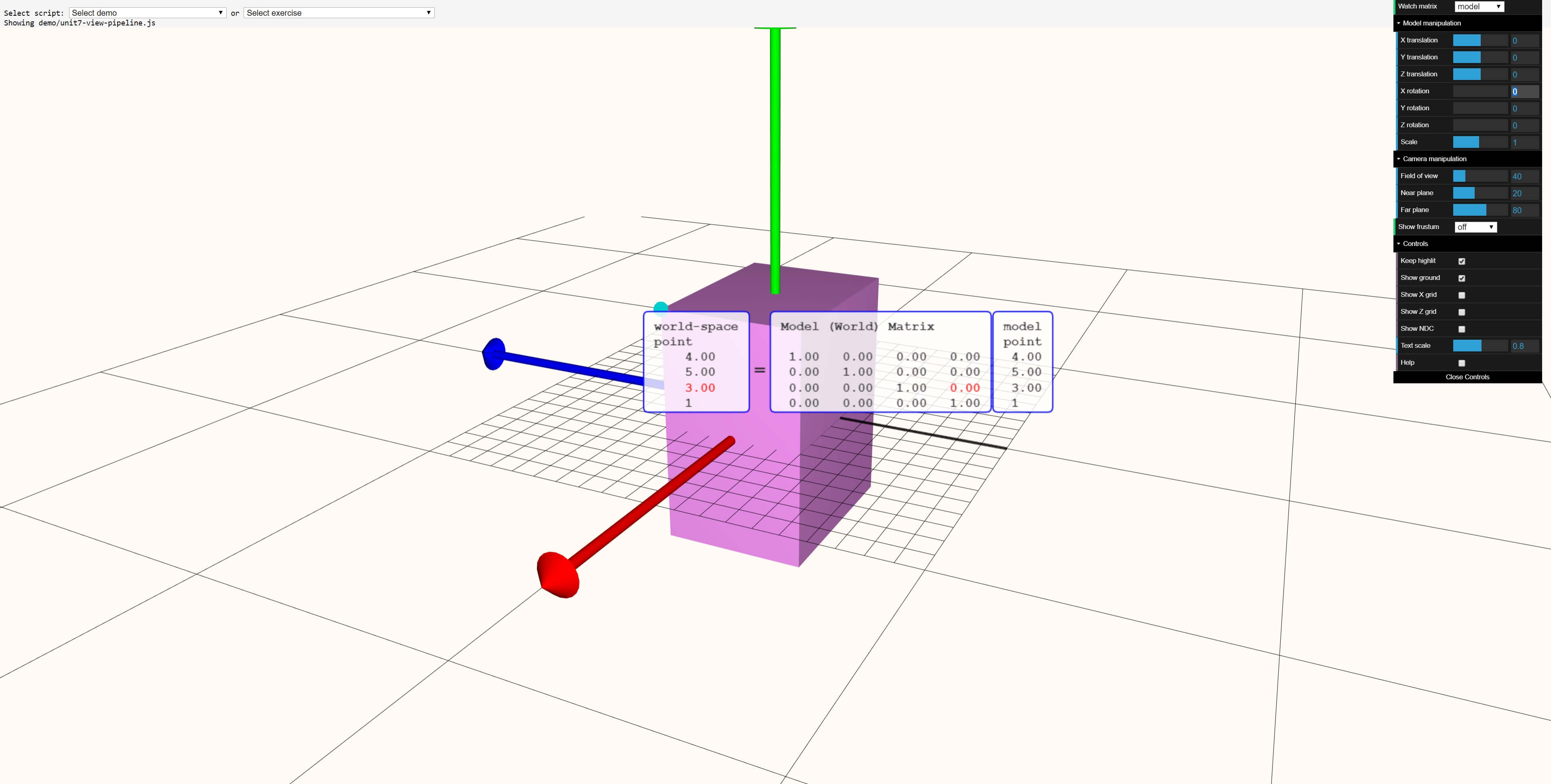
В этом онлайн-инструменте model point является вектором позиции, world matrix — матрицей преобразования, а world-space point — вектором позиции для преобразованной вершины.

Давайте применим к параллелепипеду различные преобразования:


На показанном выше изображении фигура была перенесена на 5 единиц по каждом из осей. Эти значения можно видеть в последнем столбце средней большой матрицы. Исходный вектор позиции (4, 5, 3, 1) остаётся таким же, как и должен, но преобразованная вершина теперь перенесена в (9, 10, 8, 1).


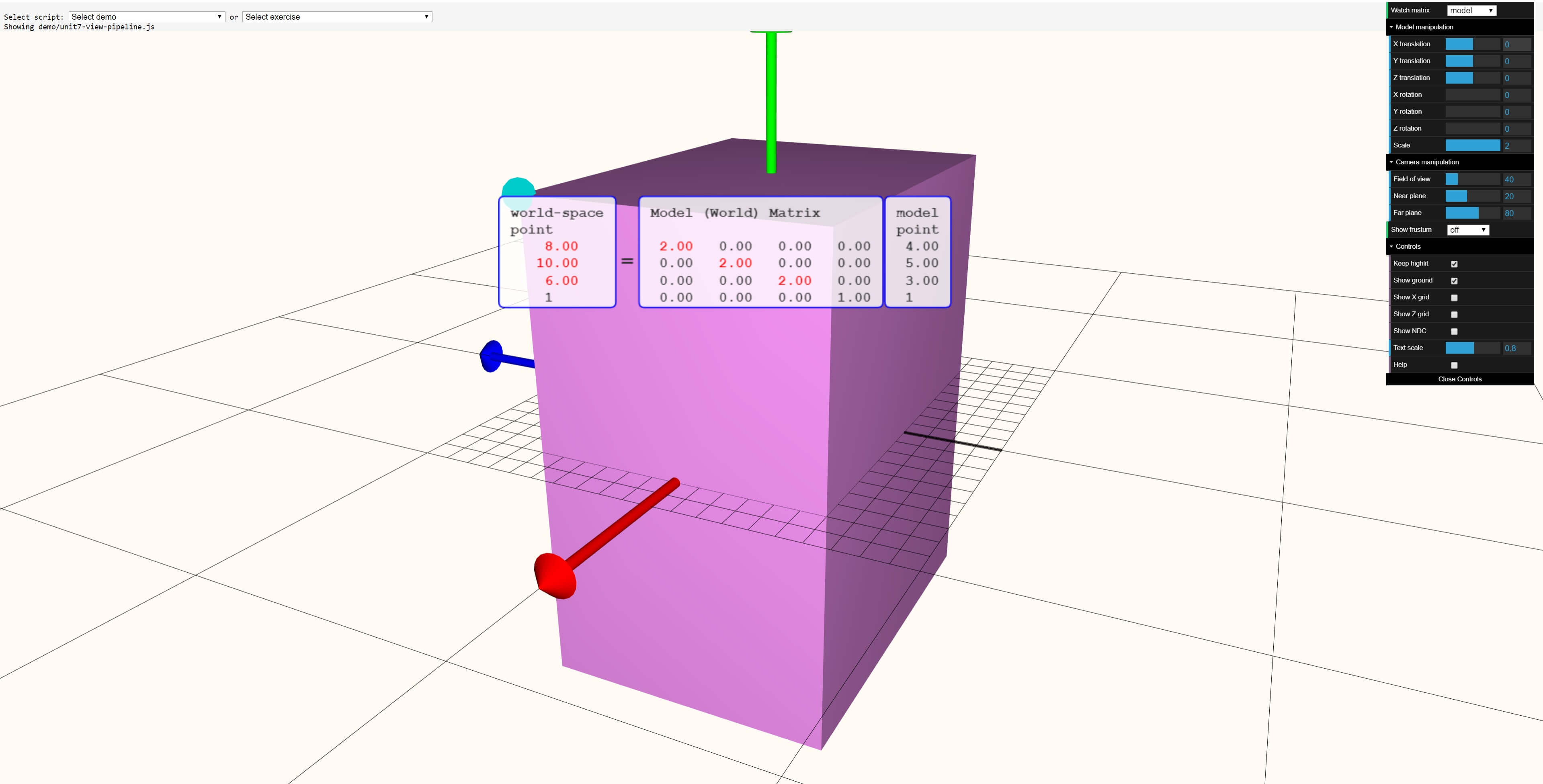
В это преобразовании всё было отмасштабировано на коэффициент 2: теперь стороны параллелепипеда стали в два раза длинее. Наконец, посмотрим на пример поворота:



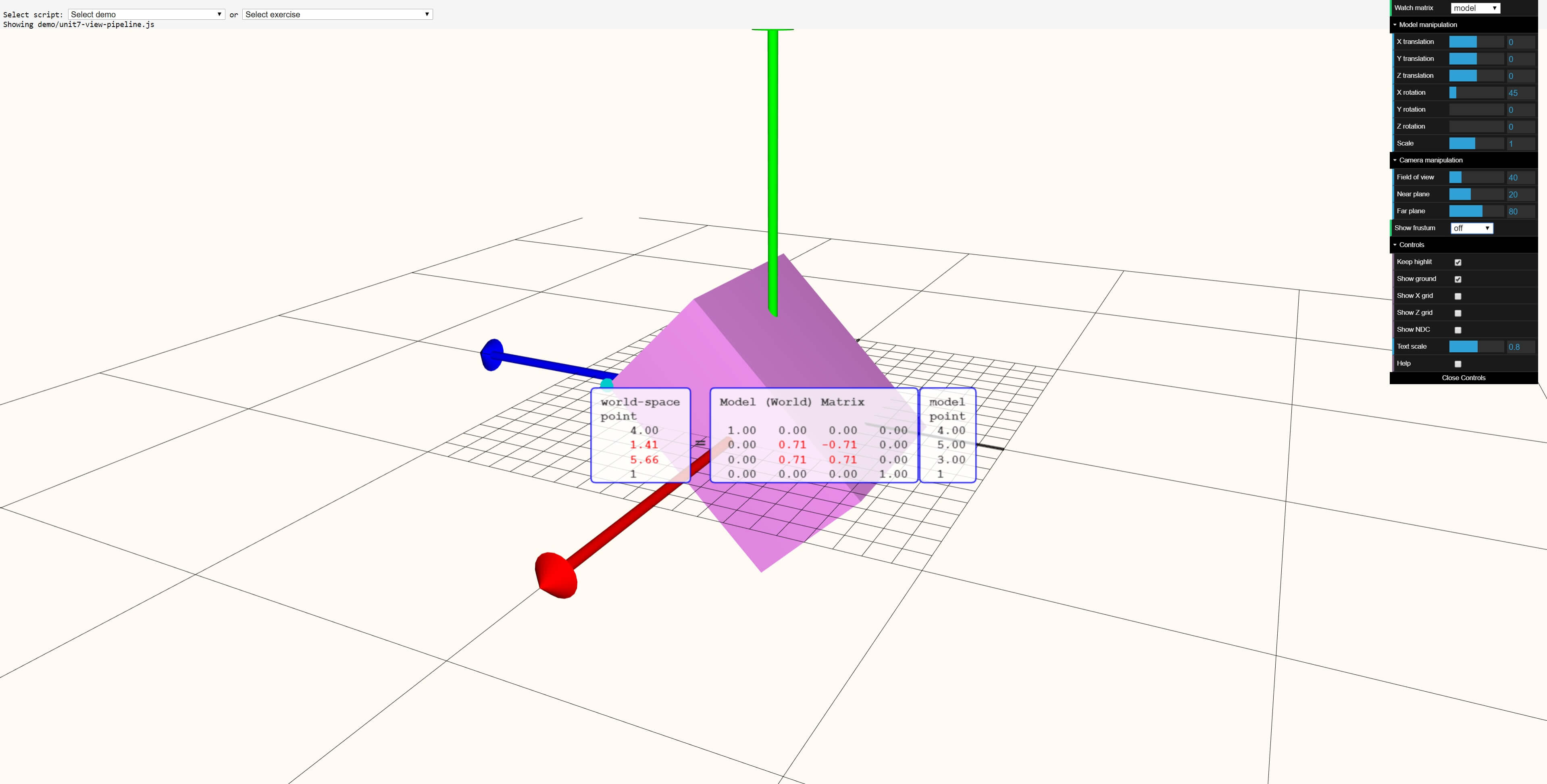
Параллелепипед был повёрнут на угол 45°, но в матрице используются синус и косинус этого угла. Проверив на научном калькуляторе, мы можем увидеть, что sin(45°) = 0.7071..., что округляется до показанного значения 0.71. Тот же ответ мы получим для значения косинуса.

Матрицы и векторы использовать не обязательно; популярной альтернативой для них, особенно в случае обработки сложных поворотов, является использование комплексных чисел и кватернионов. Эти вычисления сильно отличаются от векторов, поэтому мы не будем их рассматривать, продолжив работать с преобразованиями.

Мощь вершинного шейдера

На этом этапе нам нужно уяснить, что всем этим занимаются люди, программирующие код рендеринга. Если разработчик игр использует сторонний движок (например, Unity или Unreal), то всё это уже сделано за него; но если кто-то делает свой движок с нуля, то ему придётся выполнять все эти вычисления с вершинами.

Но как всё это выглядит с точки зрения кода?

Чтобы понять это, мы воспользуемся примерами с потрясающего веб-сайта Braynzar Soft. Если вы хотите самостоятельно начать работу с 3D-программированием, то это подходящее место для изучения основ, а также более сложных вещей…


Это пример преобразования «всё в одном». Он создаёт соответствующие матрицы преобразования на основании ввода с клавиатуры, а затем применяет их к исходному вектору позиции за одну операцию. Заметьте, что это всегда выполняется в заданном порядке (масштабирование — поворот — перенос), потому что любой другой способ совершенно испортит результат.

Такие блоки кода называются вершинными шейдерами (vertex shaders), их сложность и размер могут варьироваться в огромных масштабах. Показанный выше пример прост, это только вершинный шейдер, не использующий полной программируемой природы шейдеров. Более сложная последовательность шейдеров могла бы преобразовывать объекты в 3D-пространстве, обрабатывать их внешний вид с точки зрения камеры сцены, а затем передавать данные на следующий этапе процесса рендеринга. Рассматривая порядок обработки вершин, мы изучим и другие примеры.

Разумеется, они могут использоваться для гораздо большего, поэтому, играя в 3D-игру, не забывайте, что всё движение, которое вы видите, выполнено графическим процессором, исполняющим команды вершинных шейдеров.

Однако так было не всегда. Если вернуться в середину-конец 1990-х, то графические карты той эпохи не имели возможности самостоятельно обрабатывать вершины и примитивы, всем этим в одиночку занимался центральный процессор.


Одним из первых процессоров, имеющих собственное аппаратное ускорение данного процесса, был Nvidia GeForce, выпущенный в 2000 году, и эту функциональность назвали Hardware Transform and Lighting (сокращённо Hardware TnL). Процессы, которые могло обрабатывать это оборудование, были очень ограниченными с точки зрения команд, но с выходом новых чипов ситуация быстро менялась. Сегодня не существует отдельного оборудования для обработки вершин и одно устройство занимается всем сразу: точками, примитивами, пикселями, текстурами и т.д.

К слову, об освещении (lighting): стоит заметить, что мы видим всё благодаря свету, поэтому давайте посмотрим, как его можно обрабатывать на этапе вершин. Для этого нам нужно воспользоваться тем, о чём мы говорили ранее.

Свет, камера, мотор!

Представьте такую картину: игрок стоит в тёмной комнате, освещённой одним источником света справа. В середине комнаты висит огромный чайник. Возможно, для этого вам понадобится помощь, поэтому давайте воспользуемся веб-сайтом Real-Time Rendering, и увидим, как это будет выглядеть:


Не забывайте, что этот объект является набором соединённых вместе плоских треугольников; то есть плоскость каждого треугольника будет направлена в определённую сторону. Некоторые из них направлены в сторону камеры, некоторые — в другую, некоторые будут искажены. Свет от источника падает на каждую плоскость и отражается от неё под определённым углом.

В зависимости от того, куда отразился свет, могут меняться цвет и яркость плоскости, и чтобы цвет объекта выглядел правильно, всё это нужно вычислить и учесть.

Начнём с того, что нам нужно узнать, куда направлена каждая плоскость, и для этого нам потребуется вектор нормали (normal vector) плоскости. Это ещё одна стрелка, но в отличие от вектора позиции, её размер не важен (на самом деле после вычисления масштаб векторов нормалей всегда уменьшается чтобы они имели длину 1), и она всегда направлена перпендикулярно (под прямым углом) к плоскости.


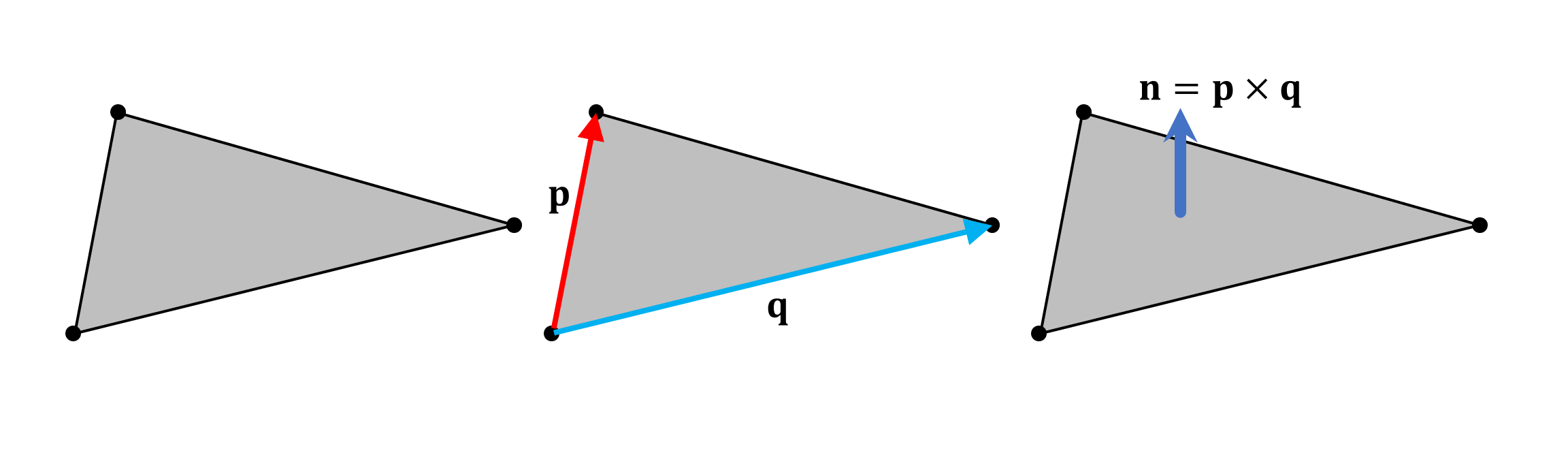
Нормаль к плоскости каждого треугольника вычисляется определением векторного произведения двух векторов направления (показанных выше p и q), образующих стороны треугольника. На самом деле лучше вычислять их для каждой вершины, а не для треугольника, но поскольку первых всегда больше, чем вторых, быстрее будет вычислять нормали для треугольников.

Получив нормаль к поверхности, можно начать учитывать источник освещения и камеру. В 3D-рендеринге источники освещения могут быть разного типа, но в этой статье мы будем рассматривать только направленные источники, например, прожекторы. Как и плоскость треугольника, прожектор и камера будут указывать в определённом направлении, примерно так:


Вектор источника освещения и вектор нормали можно использовать для вычисления угла, под которым свет падает на поверхность (используя отношение между скалярным произведением векторов и произведением их размеров). Вершины треугольника будут содержать дополнительную информацию о своём цвете и материале. Материал описывает, что происходит со светом, когда он падает на поверхность.

Гладкая металлическая поверхность будет отражать почти весь падающий свет под тем углом, под которым он упал, и едва изменит цвет объекта. Шероховатый матовый материал рассеивает свет менее предсказуемым образом и немного меняет цвет. Чтобы учесть это, нужно добавить вершинам дополнительные значения:

• Исходный базовый цвет
• Атрибут материала Ambient — значение, определяющее, сколько «фонового» освещения может поглотить и отразить вершина
• Атрибут материала Diffuse — ещё одно значение, но на этот раз определяющее «шероховатость» вершины, что, в свою очередь, влияет на величину поглощения и отражения рассеянного света
• Атрибуты материала Specular — два значения, задающие величину «блеска» вершины

В разных моделях освещения используются разные математические формулы для группировки всех этих атрибутов, а результатом вычислений становится вектор исходящего освещения. В сочетании с вектором камеры он позволяет определить общий внешний вид треугольника.


Один направленный источник освещения освещает множество различных материалов из демо Nvidia

Мы опустили многие подробные детали, и на то есть уважительная причина: откройте любой учебник по 3D-рендерингу, и вы увидите, что этому процессу посвящены целые главы. Однако в современных играх основная часть всех вычислений освещения и эффектов материалов выполняется на этапе обработки пикселей, поэтому мы вернёмся к ним в следующей статье.


Пример кода B. Anguelov, показывающий, как в вершинном шейдере можно обрабатывать модель отражения света по Фонгу.

Всё, что мы рассматривали выше, выполняется вершинными шейдерами, и кажется, что для них нет ничего невозможного; к несчастью, это не так. Вершинные шейдеры не могут создавать новых вершин и каждый шейдер должен обрабатывать каждую отдельную вершину. Было бы удобно, если бы можно было использовать код для создания новых треугольников между тех, которые мы уже имеем (для повышения визуального качества), и иметь шейдер, обрабатывающий целый примитив (чтобы ускорить обработку). Ну, в современных графических процессорах мы можем это сделать!

Пожалуйста, сэр, мне хочется ещё (треугольников)

Современные графические чипы чрезвычайно мощны и способны каждую секунду выполнять миллионы матрично-векторных вычислений; они с лёгкостью справляются с огромной кучей вершин за раз. С другой стороны, создание высокодетализированных моделей для рендеринга — это очень долгий процесс, и если модель будет находиться на каком-то расстоянии от сцены, то все эти детали пропадут впустую.

То есть нам нужно каким-то образом приказать процессору разбить большой примитив, например, один плоский треугольник на набор меньших треугольников, расположенных внутри исходного. Такой процесс называется тесселяцией (tesselation) и графические чипы уже научились выполнять его очень хорошо; за годы развития увеличивалась степень контроля, которым обладают программисты над этим процессом.

Чтобы посмотреть на это в действии, мы воспользуемся инструментом бенчмарка Heaven движка Unigine, потому что он позволяет нам применять к используемым в тесте моделям различные величины тесселяции.


Для начала давайте возьмём место в бенчмарке и изучим его без применения тесселяции. Заметьте, что булыжники на земле выглядят очень неестественными — использованная текстура эффективна, но кажется неправильной. Давайте применим к сцене тесселяцию: движок Unigine применяет её только к отдельным частям, но различие будет значительным.


Земля, края зданий и дверь выглядят намного реалистичнее. Мы можем увидеть, как это было достигнуто, запустив процесс заново, но на этот раз с выделением всех примитивов (то есть в режиме wireframe):


Чётко видно, почему земля выглядит так странно — она совершенно плоская! Дверь сливается со стенами, а края здания представляют собой простые параллелепипеды.

В Direct3D примитивы можно разделить на группу из более мелких частей (этот процесс называется подразделением (sub-division)), выполнив трёхэтапный процесс. Сначала программисты пишут шейдер поверхности (hull shader) — по сути, этот код создаёт структуру под названием патч геометрии (geometry patch). Можно воспринимать её как карту, сообщающую процессору, где внутри начального примитива будут появляться новые точки и линии.

Затем блок-тесселятор внутри графического процессора применяет этот патч к примитиву. В конце выполняется доменный шейдер (domain shader), вычисляющий позиции всех новых вершин. Эти данные при необходимости можно передать обратно в буфер вершин, чтобы можно было заново выполнить вычисления освещения, но на этот раз с более качественными результатами.

Как же это выглядит? Давайте запустим каркасную версию тесселированной сцены:


Честно говоря, мы задали довольно высокую степень тесселяции, чтобы объяснение процесса было нагляднее. Как бы ни были хороши современные графические чипы, такое не стоит проделывать в каждой сцене — посмотрите, например, на фонарь рядом с дверью.

В изображениях с отключенным режимом wireframe вы бы с трудом нашли отличия на этом расстоянии, и мы видим, что такой уровень тесселяции добавил столько треугольников, что их сложно отделить друг от друга. Однако при правильном применении эта функция обработки вершин может создавать фантастические визуальные эффекты, особенно при симуляции столкновений мягких тел.

Давайте посмотрим, как это может выглядеть с точки зрения кода Direct3D; для этого мы используем пример с ещё одного замечательного веб-сайта, RasterTek.

Вот простой зелёный треугольник, тесселированный на множество крошечных треугольничков…


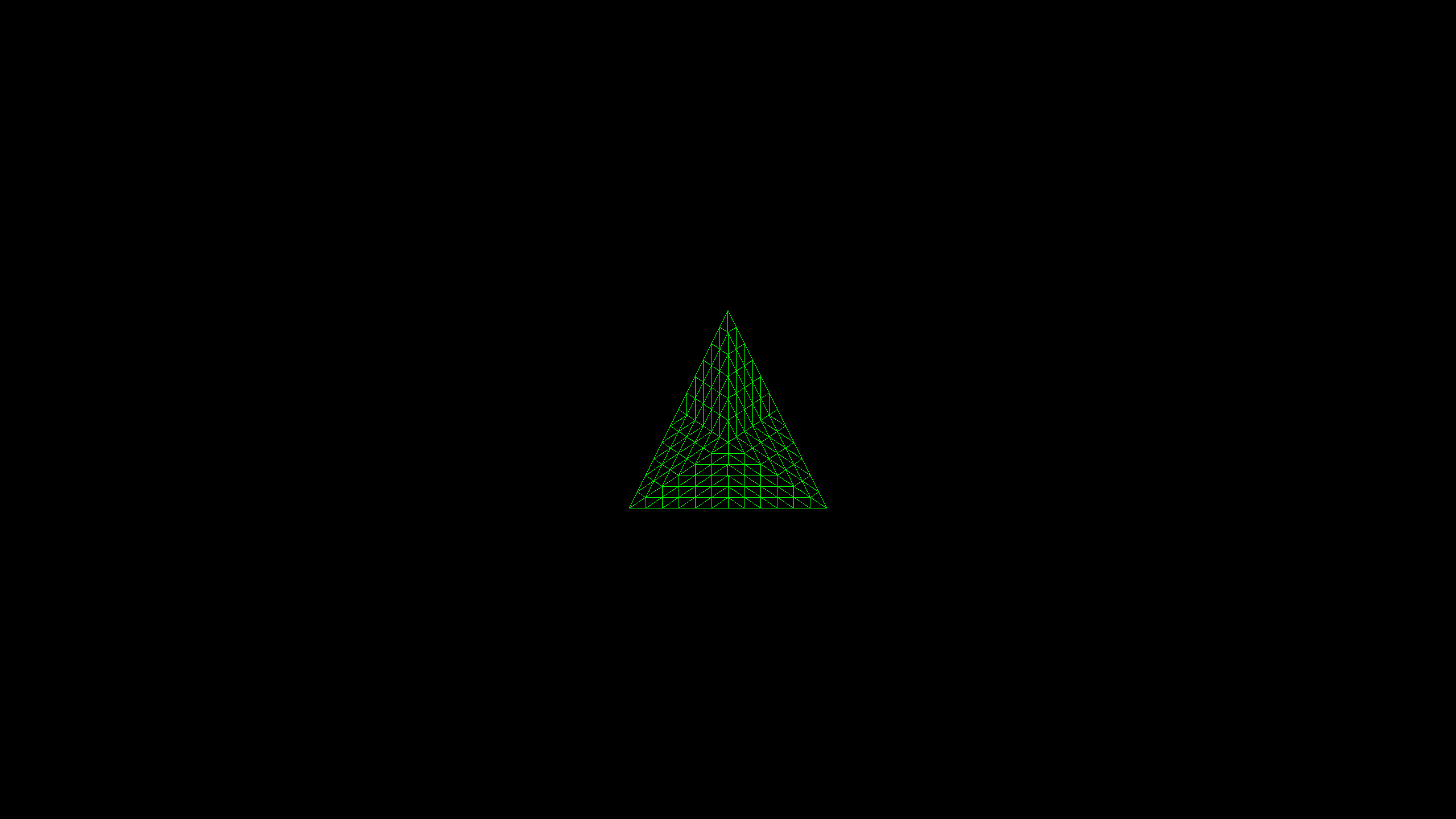
Обработка вершин выполняется тремя отдельными шейдерами (см. пример кода): вершинным шейдером, подготавливающим треугольник к тесселяции, шейдером поверхности, генерирующим патч, и доменным шейдером, обрабатывающим новые вершины. Результат достаточно понятен, но пример с движком Unigine демонстрирует и потенциальные преимущества, и опасности повсеместного использования тесселяции.

«Железо» этого не выдержит!

Помните, мы говорили, что вершинные шейдеры всегда обрабатывают каждую отдельную вершину в сцене? Несложно понять, что тесселяция может стать здесь серьёзной проблемой. И существует множество визуальных эффектов, где нужно обрабатывать различные версии одного примитива, но без создания их с самого начала, например, волосы, мех, трава и частицы взрывов.

К счастью, специально для таких вещей существует ещё один шейдер — геометрический шейдер. Это более ограниченная версия вершинного шейдера, но он может быть применён к целому примитиву. В сочетании с тесселяцией он создаёт программистам повышенный контроль над большими группами вершин.


UL Benchmark's 3DMark Vantage — геометрические шейдеры обрабатывают частицы и флаги

Direct3D, как и все современные графические API, позволяет выполнять с вершинами большое множество вычислений. Готовые данные могут быть или переданы на следующий этап процесса рендеринга (растеризацию), или вернуться в пул памяти для повторной обработки или считывания центральным процессором для других целей. Как сказано в документации Microsoft по Direct3D, это можно реализовать как поток данных:


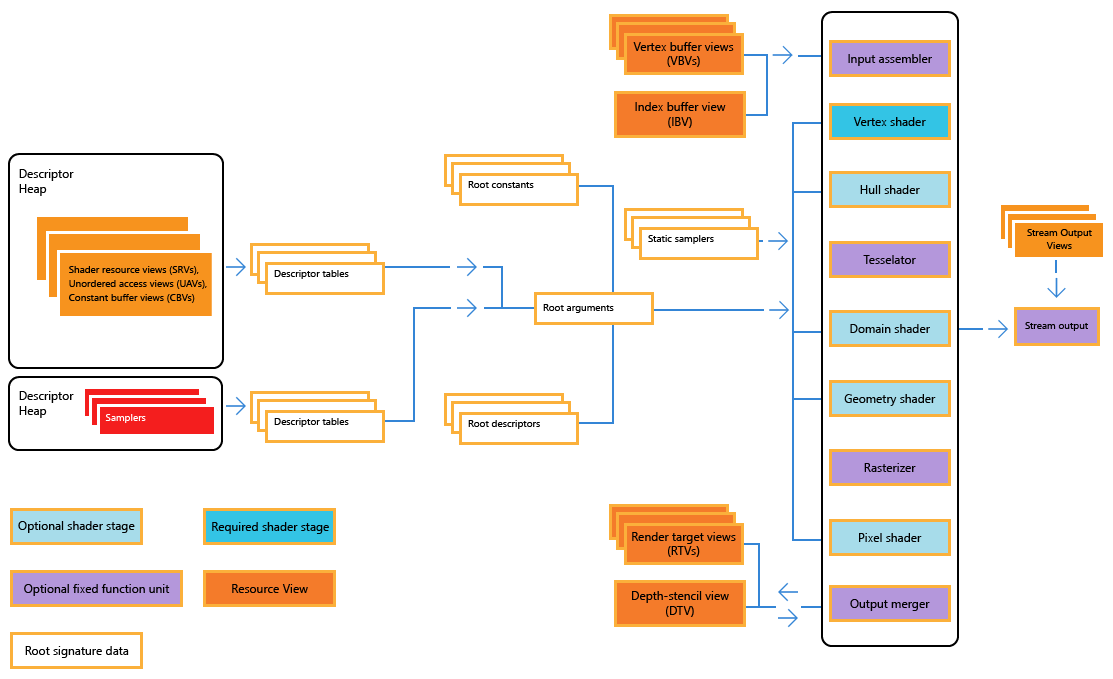
Этап вывода потока (stream output) необязателен, особенно потому, что он может передавать обратно в цикл рендеринга только целые примитивы (а не отдельные вершины), но он полезен для эффектов, требующих большого количества частиц. Такой же трюк можно провернуть при помощи изменяемого или динамического вершинного буфера, но буферы входящих данных лучше хранить неизменными, потому что при их открытии для изменения снижается производительность.

Обработка вершин — это критически важная часть рендеринга, потому что она определяет, как будет выглядеть сцена с точки зрения камеры. В современных играх для построения миров могут использоваться миллионы треугольников, и каждая из этих вершин каким-то образом преобразуется и освещается.


Треугольники. Их миллионы.

Обработка всех этих вычислений и математики может показаться логистическим кошмаром, но графические процессоры (GPU) и API разрабатываются с учётом всего этого — представьте идеально работающую фабрику, пропускающую через производственный конвейер по одному изделию за раз.

Опытные программисты рендеринга 3D-игр имеют фундаментальные знания в области математики и физики; они используют все возможные трюки и инструменты для оптимизации операций, сжимая этап обработки вершин всего до нескольких миллисекунд. А ведь это только самое начало построения 3D-кадра — следующим идёт этап растеризации, затем чрезвычайно сложная обработка пикселей и текстур, и уже потом изображение попадает на монитор.