11.12.2019 04:34
PatientZero 5 4700 Источник
image

Пару лет назад я написал очень простую реализацию фрактального сжатия изображений для студенческой работы и выложил код на github.

К моему удивлению, репозиторий оказался довольно популярным, поэтому я решил обновить код и написать статью, объясняющую его и теорию.

Теория


Эта часть довольно теоретическая, и если вас интересует только документация к коду, можете её пропустить.

Сжимающие отображения


Пусть $(E, d)$ — полное метрическое пространство, а $f : E \rightarrow E$ — отображение из $E$ на $E$.

Мы говорим, что $f$ является сжимающим отображением, если существует $0 < s < 1$, такое, что:

$\forall x, y \in E, d(f(x), f(y)) \leq sd(x, y)$


Исходя из этого, $f$ будет обозначать сжимающее отображение с коэффициентом сжимания $s$.

О сжимающих отображениях существует две важные теоремы: теорема Банаха о неподвижной точке и теорема коллажа.

Теорема о неподвижной точке: $f$ имеет уникальную неподвижную точку $x_0$.

Показать доказательство
Сначала докажем, что последовательность $(u_n)$, заданная как $inline$\left\{\begin{alignat*}{2}u_0 & = x\\ u_{n+1} & = f(u_n)\end{alignat*}\right.$inline$ является сходящейся для всех $x \in E$.

Для всех $m < n \in \mathbb{N}$:

$\begin{alignat*}{2} d(u_m, u_n) & = d(f^m(x), f^n(x)) \\ & \leq s^md(x, f^{n-m}(x)) \text{ поскольку} f \text{ - это сжимающее отображение} \\ & \leq s^m\left(\sum_{i=0}^{n-m-1}{d(f^i(x), f^{i+1}(x))}\right) \text{ из неравенства треугольника} \\ & \leq s^m\left(\sum_{i=0}^{n-m-1}{s^id(x, f(x))}\right) \text{ поскольку} f \text{ - сжимающее отображение} \\ & = s^m\left(\frac{1 - s^{n-m}}{1 - s}d(x, f(x))\right) \\ & \leq \frac{s^m}{1 - s}d(x, f(x)) \underset{m \rightarrow \infty}{\rightarrow} 0 \end{alignat*}$


Следовательно, $(u_n)$ является последовательностью Коши, и $E$ является полным пространством, а значит, $(u_n)$ является сходящейся. Пусть её пределом будет $x_0$.

Более того, поскольку сжимающее отображение является непрерывным как липшицево отображение, оно также является непрерывным, то есть $f(u_n) \rightarrow f(x_0)$. Следовательно, если $n$ стремится к бесконечности в $u_{n+1} = f(u_n)$, мы получаем $x_0 = f(x_0)$. То есть $x_0$ является неподвижной точкой $f$.

Мы показали, что $f$ имеет неподвижную точку. Давайте при помощи противоречия покажем, что она уникальна. Пусть $y_0$ — ещё одна неподвижная точка. Тогда:

$d(x_0, y_0) = d(f(x_0), f(y_0)) \leq sd(x_0, y_0) < d(x_0, y_0)$


Возникло противоречие.

Далее мы будем обозначать как $x_0$ неподвижную точку $f$.

Теорема коллажа: если $d(x, f(x)) < \epsilon$, то $d(x, x_0) < \frac{\epsilon}{1 - s}$.

Показать доказательство
В предыдущем доказательстве мы показали, что $d(u_m, u_n) \leq \frac{s^m}{1 - s}d(x, f(x)) = \frac{s^m}{1 - s}\epsilon$.

Если мы зафиксируем $m$ в $0$, то получим $d(x, u_n) \leq \frac{\epsilon}{1 - s}$.

При стремлении $n$ к бесконечности мы получим требуемый результат.

Вторая теорема говорит нам, что если мы найдём сжимающее отображение $f$, такое, что $f(x)$ близко к $x$, то можем быть уверенными, что неподвижная точка $f$ тоже находится близко к $x$.

Этот результат будет фундаментом для нашей дальнейшей работы. И в самом деле, вместо сохранения изображения нам достаточно сохранить сжимающее отображение, неподвижная точка которого близка к изображению.

Сжимающие отображения для изображений


В этой части я покажу, как создавать такие сжимающие отображения, чтобы неподвижная точка находилась близко к изображению.

Сначала давайте зададим множество изображения и расстояние. Мы выберем $E = [0, 1]^{h \times w}$. $E$ — это множество матриц с $h$ строками, $w$ столбцами и с коэффициентами в интервале $[0, 1]$. Затем мы возьмём $d(x, y) = \left(\sum_{i=1}^{h}{\sum_{j=1}^{w}{(x_{ij}-y_{ij})^2}}\right)^{0.5}$. $d$ — это расстояние, полученное из нормы Фробениуса.

Пусть $x \in E$ — это изображение, которое мы хотим сжать.

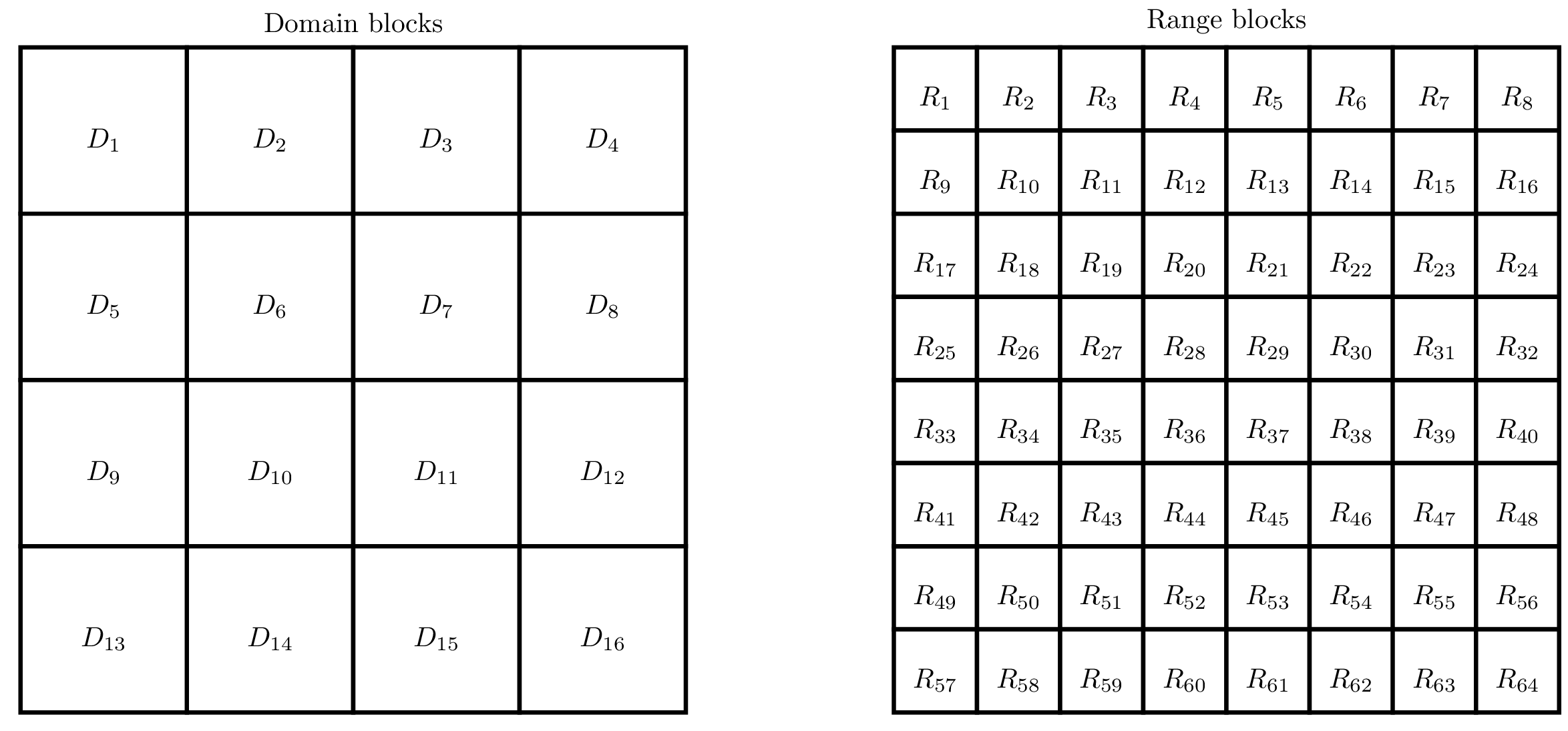
Мы дважды разделим изображение на блоки:

  • Сначала мы разделим изображение на конечные или интервальные блоки $R_1, ..., R_L$. Эти блоки разделены и покрывают изображение целиком.
  • Затем мы разделяем изображение на блоки источников или доменов $D_1, ..., D_K$. Эти блоки необязательно разделены и необязательно покрывают всё изображение.

Например, мы можем сегментировать изображение следующим образом:


Затем для каждого блока интервала $R_l$ мы выбираем блок домена $D_{k_l}$ и отображение $f_l : [0, 1]^{D_{k_l}} \rightarrow [0, 1]^{R_{l}}$.

Далее мы можем определить функцию $f$ как:

$f(x)_{ij} = f_l(x_{D_{k_l}})_{ij} \text{ if } (i, j) \in R_l$


Утверждение: если $f_l$ являются сжимающими отображениями, то и $f$ тоже сжимающее отображение.

Показать доказательство
Пусть $x, y \in E$ и предположим, что все $f_l$ являются сжимающими отображениями с коэффициентом сжимания $s_l$. Тогда получаем следующее:

$\begin{alignat*}{2} d(f(x), f(y))^2 & = \sum_{i=1}^{h}{\sum_{j=1}^{w}{(f(x)_{ij}-f(y)_{ij})^2}} \text{ по определению } d \\ & = \sum_{l=1}^L{\sum_{(i,j) \in R_l}{(f(x)_{ij}-f(y)_{ij})^2}} \text{ поскольку } (R_l) \text{ является разбиением} \\ & = \sum_{l=1}^L{\sum_{(i,j) \in R_l}{(f_l(x_{D_{k_l}})_{ij}-f_l(y_{D_{k_l}})_{ij})^2}} \text{ по определению } f \\ & = \sum_{l=1}^L{d(f_l(x_{D_{k_l}}), f_l(y_{D_{k_l}}))^2} \text{ по определению } d \\ & \leq \sum_{l=1}^L{s_l^2d(x_{D_{k_l}}, y_{D_{k_l}})^2} \text{ поскольку } (f_l) \text{ являются сжимающими отображениями} \\ & \leq \underset{l}{\max}{s_l^2}\sum_{l=1}^L{d(x_{D_{k_l}}, y_{D_{k_l}})^2} \\ & = \underset{l}{\max}{s_l^2}\sum_{l=1}^L{\sum_{(i,j) \in R_l}{(x_{ij}-y_{ij})^2}} \text{ по определению } d \\ & = \underset{l}{\max}{s_l^2}\sum_{i=1}^{h}{\sum_{j=1}^{w}{(x_{ij}-y_{ij})^2}} \text{ поскольку } (R_l) \text{ является разбиением} \\ & = \underset{l}{\max}{s_l^2}d(x, y)^2 \text{ по определению } d \\ \end{alignat*}$


Остаётся один вопрос, на который нужно ответить: как выбрать $D_{k_l}$ и $f_l$?

Теорема коллажа предлагает способ их выбора: если $x_{R_l}$ находится близко к $f(x_{D_{k_l}})$ для всех $l$, то $x$ находится близко к $f(x)$ и по теореме коллажа $x$ и $x_0$ тоже находятся близко.

Таким образом мы независимо для каждого $l$ можем построить множество сжимающих отображений из каждого $D_{k}$ на $R_l$ и выбрать наилучшее. В следующем разделе мы покажем все подробности этой операции.

Реализация


В каждый раздел я буду копировать интересные фрагменты кода, а весь скрипт можно найти здесь.

Разбиения


Я выбрал очень простой подход. Блоки источников и конечные блоки сегментируют изображение по сетке, как показано на изображении выше.

Размер блоков равен степеням двойки и это очень упрощает работу. Блоки источников имеют размер 8 на 8, а конечные блоки — 4 на 4.

Существуют и более сложные схемы разбиения. Например, мы можем использовать дерево квадрантов (quadtree), чтобы сильнее разбивать области с большим количеством деталей.

Преобразования


В этом разделе я покажу, как создавать сжимающие отображения из $D_{k}$ на $R_l$.

Помните, что мы хотим сгенерировать такое отображение $f_l$, чтобы $f(x_{D_k})$ было близко к $x_{R_l}$. То есть чем больше отображений мы сгенерируем, тем больше вероятность найти хорошее.

Однако качество сжатия зависит от количества битов, необходимых для сохранения $f_l$. То есть если множество функций будет слишком большим, то сжатие окажется плохим. Здесь нужно искать компромисс.

Я решил, что $f_l$ будет иметь следующий вид:

$f_l(x_{D_k}) = s \times rotate_{\theta}(flip_d(reduce(x_{D_k}))) + b$


где $reduce$ — это функция для перехода от блоков 8 на 8 к блокам 4 на 4, $flip$ и $rotate$ — аффинные преобразования, $s$ изменяет контрастность, а $b$ — яркость.

Функция reduce снижает размер изображения, усредняя окрестности:

def reduce(img, factor):
    result = np.zeros((img.shape[0] // factor, img.shape[1] // factor))
    for i in range(result.shape[0]):
        for j in range(result.shape[1]):
            result[i,j] = np.mean(img[i*factor:(i+1)*factor,j*factor:(j+1)*factor])
    return result

Функция rotate поворачивает изображение на заданный угол:

def rotate(img, angle):
    return ndimage.rotate(img, angle, reshape=False)

Для сохранения формы изображения угол $\theta$ может принимать только значения $\{0^{\circ}, 90^{\circ}, 180^{\circ}, 270^{\circ}\}$.

Функция flip отражает изображение зеркально, если direction равно -1 и не отражает, если значение равно 1:

def flip(img, direction):
    return img[::direction,:]

Полное преобразование выполняется функцией apply_transformation:

def apply_transformation(img, direction, angle, contrast=1.0, brightness=0.0):
    return contrast*rotate(flip(img, direction), angle) + brightness

Нам нужен 1 бит, чтобы запомнить, требуется ли зеркальное отражение, и 2 бита для угла поворота. Более того, если мы сохраним $s$ и $b$, использовав по 8 бит на каждую величину, то для сохранения преобразования нам в целом понадобится всего 11 битов.

Кроме того, нам следует проверять, являются ли эти функции сжимающими отображениями. Доказательство этого немного скучно, и не особо нам нужно. Возможно, позже я добавлю его как приложение к статье.

Сжатие


Алгоритм сжатия прост. Сначала мы генерируем все возможные аффинные преобразования всех блоков источников при помощи функции generate_all_transformed_blocks:

def generate_all_transformed_blocks(img, source_size, destination_size, step):
    factor = source_size // destination_size
    transformed_blocks = []
    for k in range((img.shape[0] - source_size) // step + 1):
        for l in range((img.shape[1] - source_size) // step + 1):
            # Extract the source block and reduce it to the shape of a destination block
            S = reduce(img[k*step:k*step+source_size,l*step:l*step+source_size], factor)
            # Generate all possible transformed blocks
            for direction, angle in candidates:
                transformed_blocks.append((k, l, direction, angle, apply_transform(S, direction, angle)))
    return transformed_blocks

Затем для каждого конечного блока мы проверяем все ранее сгенерированные преобразованные блоки источников. Для каждого мы оптимизируем контрастность и яркость с помощью метода find_contrast_and_brightness2, и если протестированное преобразование наилучшее из всех пока найденных, то сохраняем его:

def compress(img, source_size, destination_size, step):
    transformations = []
    transformed_blocks = generate_all_transformed_blocks(img, source_size, destination_size, step)
    for i in range(img.shape[0] // destination_size):
        transformations.append([])
        for j in range(img.shape[1] // destination_size):
            print(i, j)
            transformations[i].append(None)
            min_d = float('inf')
            # Extract the destination block
            D = img[i*destination_size:(i+1)*destination_size,j*destination_size:(j+1)*destination_size]
            # Test all possible transformations and take the best one
            for k, l, direction, angle, S in transformed_blocks:
                contrast, brightness = find_contrast_and_brightness2(D, S)
                S = contrast*S + brightness
                d = np.sum(np.square(D - S))
                if d < min_d:
                    min_d = d
                    transformations[i][j] = (k, l, direction, angle, contrast, brightness)
    return transformations

Для нахождения наилучшей контрастности и яркости метод find_contrast_and_brightness2 просто решает задачу наименьших квадратов:

def find_contrast_and_brightness2(D, S):
    # Fit the contrast and the brightness
    A = np.concatenate((np.ones((S.size, 1)), np.reshape(S, (S.size, 1))), axis=1)
    b = np.reshape(D, (D.size,))
    x, _, _, _ = np.linalg.lstsq(A, b)
    return x[1], x[0]

Распаковка


Алгоритм распаковки ещё проще. Мы начинаем с полностью случайного изображения, а затем несколько раз применяем сжимающее отображение $f$:

def decompress(transformations, source_size, destination_size, step, nb_iter=8):
    factor = source_size // destination_size
    height = len(transformations) * destination_size
    width = len(transformations[0]) * destination_size
    iterations = [np.random.randint(0, 256, (height, width))]
    cur_img = np.zeros((height, width))
    for i_iter in range(nb_iter):
        print(i_iter)
        for i in range(len(transformations)):
            for j in range(len(transformations[i])):
                # Apply transform
                k, l, flip, angle, contrast, brightness = transformations[i][j]
                S = reduce(iterations[-1][k*step:k*step+source_size,l*step:l*step+source_size], factor)
                D = apply_transformation(S, flip, angle, contrast, brightness)
                cur_img[i*destination_size:(i+1)*destination_size,j*destination_size:(j+1)*destination_size] = D
        iterations.append(cur_img)
        cur_img = np.zeros((height, width))
    return iterations

Этот алгоритм срабатывает, потому что сжимающее отображение имеет уникальную неподвижную точку, и какое бы исходное изображение мы ни выбрали, мы будем стремиться к нему.

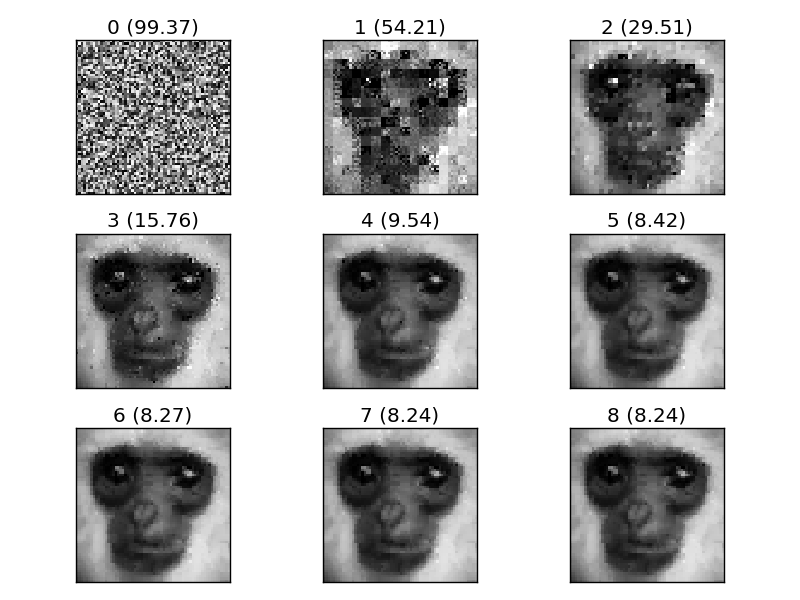
Думаю, настало время для небольшого примера. Я попробую сжать и распаковать изображение обезьяны:


Функция test_greyscale загружает изображение, сжимает его, распаковывает и показывает каждую итерацию распаковки:


Совсем неплохо для такой простой реализации!

RGB-изображения


Очень наивный подход к сжатию RGB-изображений заключается в сжатии всех трёх каналов по отдельности:

def compress_rgb(img, source_size, destination_size, step):
    img_r, img_g, img_b = extract_rgb(img)
    return [compress(img_r, source_size, destination_size, step),         compress(img_g, source_size, destination_size, step),         compress(img_b, source_size, destination_size, step)]

А для распаковки мы просто распаковываем по отдельности данные трёх каналов и собираем их в три канала изображения:

def decompress_rgb(transformations, source_size, destination_size, step, nb_iter=8):
    img_r = decompress(transformations[0], source_size, destination_size, step, nb_iter)[-1]
    img_g = decompress(transformations[1], source_size, destination_size, step, nb_iter)[-1]
    img_b = decompress(transformations[2], source_size, destination_size, step, nb_iter)[-1]
    return assemble_rbg(img_r, img_g, img_b)

Ещё одно очень простое решение заключается в использовании для всех трёх каналов одинакового сжимающего отображения, потому что часто они очень похожи.

Если хотите проверить, как это работает, то запустите функцию test_rgb: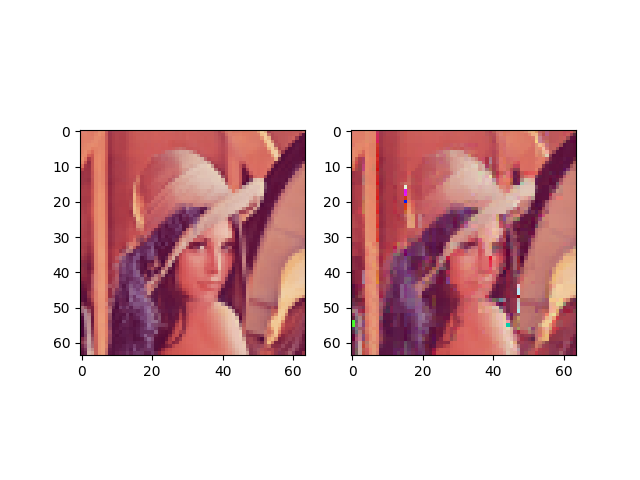


Появились артефакты. Вероятно, этот метод слишком наивен для создания хороших результатов.

Куда двигаться дальше


Если вы хотите больше узнать о фрактальном сжатии изображений, то могу порекомендовать вам прочитать статью Fractal and Wavelet Image Compression Techniques Стивена Уэлстеда. Её легко читать и в ней объяснены более сложные техники.

Комментарии (5)


  1. AndreyDmitriev
    11.12.2019 08:48
    #20989418

    С цветовыми артефактами можно попытаться побороться в цветовой модели HSI. Кроме того там можно подкрутить алгоритм для разных каналов. Надо будет попробовать на досуге.


  1. Methos
    11.12.2019 08:53
    #20989444

    В статье нет главного, зачем это нужно и сравнение с другими алгоритмами.


  1. PrinceKorwin
    11.12.2019 12:25
    #20990198

    В своё студенческое время тоже делал похожий архиватор, но упёрся в то, что всё это закопирайчено и огорождено. Хотя было очень интересно и познавательно, да.
    Интересно. Сейчас архивация на основе фрактального сжатия всё также закрыта патентами или можно таки что-то OpenSource соорудить?


  1. Cerberuser
    11.12.2019 14:38
    #20990984

    В тред призывается 3DVideo, ибо соответствующий раздел курса по сжатию медиаданных я помню, даже несмотря на то, что сам тогда всё провалил к чертям :)


  1. Gryphon88
    11.12.2019 15:42
    #20991332

    Почему традиционно считается, что мы можем сделать функцию преобразования изображения f(x,y) в f(x)*f(y)? Это ж во всех случаях не так, а для ряда преобразований ошибка будет очень большая.