Исследователи столетиями искали примеры ситуаций, в которых уравнения Эйлера для гидродинамики идеальной жидкости окажутся неверными. И вот, наконец, такой пример нашли математики.

При сближении колец жидкости в определённых упрощённых случаях описывающие их движения уравнения Эйлера не работают

Математики уже много лет подозревали, что при определённых условиях уравнения Эйлера откажутся работать. Однако они не могли описать конкретный сценарий, в котором это происходит. До сегодняшнего дня.

Эти уравнения представляют собой идеализированное математическое описание движения жидкости. В границах определённых предположений они моделируют распространение волн на пруду или просачивание патоки из банки. Они должны уметь описывать движение любой жидкости в любых условиях – и более двух столетий всё так и было.

$$

Однако новое доказательство демонстрирует, что при определённых условиях эти уравнения всё же отказываются работать.

«Полтора года назад я бы сказал, что не рассчитываю увидеть подобного развития событий ещё при своей жизни», — сказал Тарек Элгинди, математик из Калифорнийского университета в Сан-Диего, автор новой работы.

Элгинди доказал существование недостатков в уравнениях Эйлера в двух работах, опубликованных в 2019-м году – апрельскую он написал сам, а октябрьскую – в соавторстве с Теджеддином Гоулом и Надером Масмуди. Работы перевернули столетние предположения по поводу этих знаменитых уравнений для жидкости.

«Мне кажется, это прекрасное и замечательное достижение», — сказал Питер Константин, математик из Принстонского университета.

Работа Элгинди не возвещает конца уравнений Эйлера. Она доказывает, что при совершенно определённых условиях уравнения как бы перегреваются и начинают выдавать бессмыслицу. Но в более реалистичных условиях уравнения пока что остаются неуязвимыми.

Однако найденное Элгинди исключение удивило математиков, поскольку он происходит в таких условиях, при которых, как считалось ранее, уравнение должно работать в любом случае.

«В целом, мне кажется, что люди удивлены примером, приведённым Тареком», — сказал Влад Викол, математик из Нью-Йоркского университета.

Как уравнения Эйлера рванули

Леонард Эйлер вывел уравнения для жидкости, носящие ныне его имя, в 1757 году. Они описывают эволюцию жидкости со временем, так же, как уравнения Ньютона описывают движение бильярдного шара по столу.

Точнее, эти уравнения обозначают мгновенные движения бесконечно малых частиц жидкости. В их описание входит скорость частицы (насколько быстро и в каком направлении она движется) и такая связанная с ней величина, как завихрённость (насколько быстро частица вращается на манер волчка, и в каком направлении).

Вся эта информация целиком формирует «поле скоростей», мгновенный снимок движения жидкости в заданный момент времени. Уравнения Эйлера начинаются с изначального поля скоростей, и предсказывают, как оно будет меняться в любой момент в будущем.


Тарек Элгинди

Уравнения Эйлера не описывают жидкость реального мира буквально. Они включают несколько не физических предположений. К примеру, они работают, только если внутренние потоки в жидкости не создают трения, двигаясь относительно друг друга. Также предполагается несжимаемость жидкостей, то есть, по правилам уравнений Эйлера нельзя сжать жидкость, уместив её в пространство меньшего объёма, чем она уже занимает.

«Эту модель можно представить себе как идеализированный мир, а уравнения – как правила движения этого мира», — писал Владимир Сверак из Миннесотского университета нам в емейле.

Эти необычные условия позволили математику и физику Джону фон Нейману в шутку заявить, что эти уравнения моделируют поведение «сухой воды». Для моделирования более реалистичной жидкости, испытывающей внутреннее трение (т.н. вязкость), исследователи используют уравнения Навье-Стокса.

«Уравнения Эйлера очень идеализированы. В реальных жидкостях присутствует трение», — сказал Константин.

Но при этом уравнения Эйлера всё равно занимают уважаемое место в науке. Исследователям хотелось бы знать, работают эти уравнения чётко в рамках этого идеализированного мира без трения и сжатия – то есть, могут ли они описать все будущие состояния всех возможных начальных вариантов полей скорости. Или, иначе говоря: бывает ли такое движение жидкости, которое не могут моделировать эти уравнения?

«В основе своей вопрос прост: всегда ли эти уравнения выполняют свою работу?» – сказал Сверак.

В теории, подставив в уравнения значения текущего состояния жидкости, вы получите точные величины для описания её будущего состояния. Потом вы можете вновь подставить эти новые величины в уравнения, и продлить ваш прогноз. И обычно подобный процесс можно продолжать на любой отрезок времени в будущем.

Однако также возможно, что в очень редких условиях уравнения ломаются. Они могут скрипеть, пыхтеть, выдавать выходные значения, подходящие на роль будущих входных параметров, а потом вдруг выдать значение, которое для них совсем не подходит. В таких случаях математики говорят о том, что уравнения «рванули».

Если уравнения Эйлера и рванут, то это будет оттого, что они начнут усиливать скорость или завихрённость точки каким-то неестественным образом. Это усиление будет настолько сильным, что за конечное время скорость или завихрённость точки станет бесконечной. А как только уравнения выдадут бесконечное значение, они сломаются и перестанут описывать любые состояния среды в будущем. Всё потому, что обычно нельзя вести вычисления с бесконечными значениями – это всё равно, что делить на ноль (кстати, значения скорости в таком случае превысят скорость света – правда, в идеализированном мире модели это не самое страшное).

Эти роковые бесконечные значения называются «сингулярностями». Когда математики задают вопрос «всегда ли работают уравнения Эйлера?», на самом деле они спрашивают «есть ли сценарии, в которых уравнения Эйлера выдают сингулярности?»

Многие математики считают, что есть – однако до настоящего времени они не могли найти конкретный сценарий, в котором уравнения действительно взрываются.

«Складывалось ощущение, что Эйлер пытается избежать сингулярности, и до недавнего времени у него это получалось», — сказал Константин.

Новая работа не демонстрирует, как уравнения выдают сингулярности при условиях, более всего интересующих математиков. Однако пока этот результат подошёл к цели ближе остальных. И для этого Элгинди рассмотрел упрощённую модель движения жидкостей.

Уменьшая сложность

У математиков есть множество разных способов уменьшения сложности движения жидкости, для моделирования которой они используют уравнения Эйлера. Многие из наиболее интересных результатов, похожих на достигнутый Элгинди, включают демонстрацию того, насколько сильно можно упростить поведение жидкости – то есть, насколько сильно можно упростить данные, подставляемые в уравнения – и при этом ещё иметь возможность сказать что-то осмысленное касательно самих уравнений.

В реальной трёхмерной жидкости, такой, как вода в пруду, у любой частицы есть три возможных оси для движения: ось x (вправо-влево), ось y (вверх-вниз), и ось z (вперёд-назад). Довольно большая свобода перемещений. Более того, движение частиц в одной части жидкости не обязательно будет сильно связано с движением частиц в другой части.

«Приходится слишком много всего отслеживать», — сказал Элгинди.

В новой работе Элгинди упрощает работу для уравнений Эйлера. Он требует, чтобы жидкость была симметричной вдоль оси z, чего обычно в реальных жидкостях не встретишь. Благодаря симметрии становится легче подсчитать поле скоростей, поскольку известно, что точки с обеих сторон оси z зеркально симметричны. Поэтому, если вы знаете скорость или завихрённость у одной точки, нужно просто поменять знак у этих значений, и получить эти величины для другой точки.


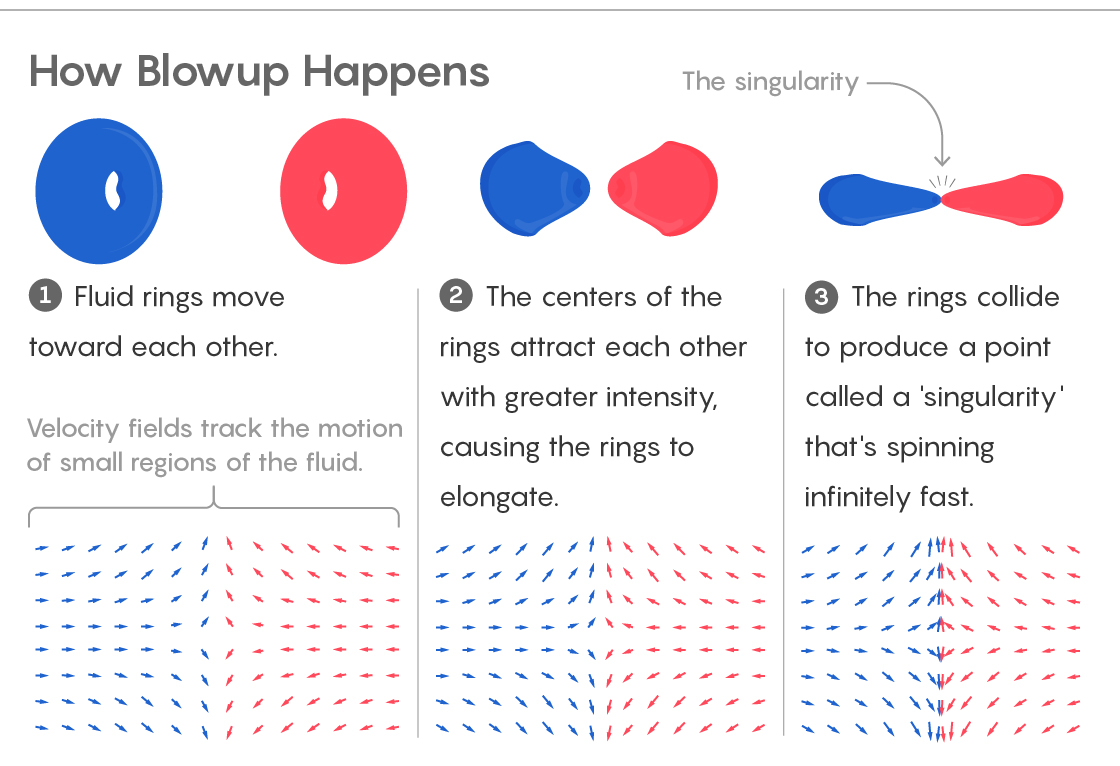
1) Жидкости двигаются навстречу. Поля скорости отслеживают движение небольших участков жидкости.
2) Центры колец притягиваются, что заставляет кольца вытягиваться.
3) Кольца сталкиваются, порождая точку «сингулярности», вращающуюся с бесконечной скоростью.

Также он ограничивает возможные перемещения точек в жидкости. Частицам можно двигаться либо вдоль оси z, либо от неё, либо по направлению к ней. Им нельзя вращаться вокруг оси z. Математики говорят, что в таких жидкостях отсутствуют водовороты.

«Это сводит задачу к двумерной», — сказал Элгинди.

Наконец, Элгинди накладывает ещё некоторые условия на изначальные данные, вводимые в уравнения Эйлера. В каком-то смысле эти данные грубее тех, что описывают реальные жидкости, и увеличивают вероятность формирования сингулярностей.

В реальной жизни, если перейти от одной точки к другой, расположенной очень близко к ней, то и скорости этих двух точек будут почти равны. Завихрённости двух этих точек тоже должны быть очень похожими. Математики говорят, что поля скорости с таким свойством «гладкие», то есть, значения на них меняются постепенно – или гладко – при движении от одной точки к другой. Быстрых изменений не происходит.

Но в случае с описанием жидкости от Элгинди всё по-другому.

«Завихрённость в данных Тарека может меняться очень сильно, — сказал Викол. – У близких точек может быть очень разная завихрённость».

Может показаться, что упрощения Элгинди очень сильно отходят от поведения реальных жидкостей для того, чтобы быть полезными. Однако они всё-таки гораздо менее жёсткие, чем многие из упрощённых сценариев, в которых учёные раньше рассматривали уравнения Эйлера. На самом деле, Элгинди даже показал, что при этих упрощённых – но не слишком – условиях уравнения Эйлера начинают выдавать очень неожиданные результаты.

Игра окончена

Чтобы понять открытие Элгинди, представьте ёмкость с водой. Это не совсем точный пример, поскольку в работе Элгинди рассматриваются жидкости, не имеющие границ, то есть, летающие, как пузырь в невесомости. Но для того, чтобы визуализировать сценарий, находящийся в центре его работы, полезно будет расположить воду в ёмкости. Хотя наиболее важные математические гипотезы – и те, что сложнее всего доказать – касаются жидкостей без границ.

Затем представьте себе два толстых кольца воды, расположенных с разных концов резервуара. Они формируют небольшие воронки, типа водоворотов – организованные возмущения внутри жидкости. Подобные явления встречаются в природе, и похожи на кольца дыма, которые умеют выдавать опытные курильщики.

Теперь представьте, как два противоположных кольца сближаются.

Во время сближения уравнения Эйлера работают нормально, подсчитывая поля скоростей, описывающие жидкость в каждый момент времени. Но когда они сближаются достаточно сильно, уравнения начинают выдавать очень странные результаты.

Они показывают, как кольца начинают притягиваться друг к другу всё сильнее и сильнее – а центральные точки колец притягиваются друг к другу ещё сильнее, чем внешние части. В итоге кольца вытягиваются, и начинают походить на воронку. И чем сильнее сближаются центры колец, тем сильнее увеличивается их скорость. А потом они сталкиваются.

И если в этот момент посмотреть на поле скорости, описывающее столкновение, можно увидеть то, что при таком наборе предположений за всю историю уравнений Эйлера никто не видел: сингулярность. Элгинди доказал, что уравнения Эйлера выдают бесконечную скорость в точке столкновения. Игра окончена.

«Классическая форма уравнения ломается, — сказал Элгинди. – После этого непонятно, что происходит».

У результата есть свои ограничения. А именно, невозможно экстраполировать поведение уравнений Эйлера в полностью «гладких» условиях на основе этого результата. Математики ещё несколько десятилетий назад доказали, что при «гладких» условиях сценарий, рассматриваемый Элгинди, не выдаст сингулярности.

Однако в остальном его результат полностью меняют взгляд математиков на эти старые уравнения.

До работы Элгинди математики не могли доказать существование какой-либо ситуации в жидкости без границ, в которой уравнения Эйлера работают некоторое время (пока кольца сближаются), но не бесконечно. Во всех предыдущих работах у математиков получалось, что если уравнения в принципе работают, то они работают всегда.

«Это весьма примечательный результат, ведь он доказывает наличие сингулярностей в сценарии, который мы называем ''корректно заданным''. Он имеет смысл, но при этом мы приходим к сингулярности за конечное время», — сказал Константин.

Многие поколения учёных искали слабое место в уравнениях Эйлера. И наконец – с некоторыми оговорками – математик нашёл его.