Все мы любим мечтать, в особенности когда это связано с посещением новых мест или возвращением в любимые места. Ничто так не воодушевляет, как чувство предвкушения планируемого события и омрачает его лишь наличие организационных моментов, в частности, выбор и покупка билетов на самолет. И почему-то внутренне мы всегда откладываем этот вопрос или перекладываем на туроператов, метапоисковики или другие агрегаторы. В практике каждого встречались ситуации, когда на экране отображалось сообщение: «К сожалению, на Ваш запрос ничего не найдено. Возможно, есть рейсы на другие дни».
Как часто случается, далеко не всегда в ответ на запрос с поиском маршрута выдается желанный результат с рейсом, который сразу же идет на оформление заказа. Мы начинаем переходить с сайта на сайт, чтобы получить удовлетворяющий ответ.
Возникновение похожих случаев сопряжено с отсутствием прямого сообщения или заранее предусмотренных комбинированных (стыковочных) маршрутов, либо предлагались маршруты с пересадками, которые включали время ожидания следующего рейса более чем 5-6 часов, а то и целые сутки.
Как же так получается, что при всем многообразии авиакомпаний мы получаем ответы, далеко не всегда нас удовлетворяющие, и вообще, как алгоритмически строятся механизмы поиска вариантов маршрутов? В этом вопросе нам на помощь приходит прикладная математика с применением алгоритмов и критериями оценки.
Карта аэропортов мира
Решением логистических задач я занимаюсь довольно давно и когда столкнулся с задачей построения поисковой системы, которая будет искать оптимальные маршруты, мне она показалась довольно тривиальной. По опыту я мог заранее сказать, что ее можно решить довольно простыми методами и в сравнительно короткие сроки. Однако, если бы все было так просто, то данная статья бы и не появилась. Поэтому, включившись в работу, через некоторое время я понял, что не такая уж она и тривиальная.
Отправной точкой, как часто это бывает в путешествиях, а именно с таким подходом я и подошел, стало решение построить транспортную сеть в виде графа. Транспортная сеть изначально включала данные по аэропортам, авиакомпаниям, их расписанию с рейсами и показатели стыковочного времени.
За основу было принято, что в качестве вершины графа рассматриваются аэропорты, а ребрами являются рейсы между ними. В результате у нас получился костяк, как в скелете, на основании которого начал накладывать расписание, которое имело свои характеристики: время отправления и прибытия. При этом движение по ребрам всегда возможно только в определенное время, что характеризуется частными вариантами решения задачи:
Сложность при этом заключается в том, что ни при каких условиях у нас нет применения только одного частного случая, запрос всегда содержит связанные между собой критерии поиска, включающие в себя один-два или более уточнений. Отсюда вытекает, что применение критериальности накладывает определенные условия на расчет искомых вариантов маршрутов. Помимо трех перечисленных выше, в расчет закладывается применение категорий классов обслуживания (первый, бизнес, эконом), стоимость, количество пассажиров и их категории, а также наличие целого ряда дополнительных услуг, влияющих на результат. Таким образом это полностью стало укладываться в мою концепцию решения задачи путем многокритериальной оптимизации (многоцелевая оптимизация), а именно — поиска кратчайшего пути по нескольким критериям (MOSP — multi-objective shortest path).
Но, как всем известно, для того, чтобы проверить одну гипотезу, надо привести ряд других. В качестве еще одного варианта решения задачи рассматривалось применение нелинейного программирования.
Учитывая, что дуги графа взвешены векторами, решение задачи можно было свести к квадратичному (нелинейному) программированию. И все бы было идеально, если бы не тот факт, что вектора, по сути, обладают всего двумя характеристиками: длиной и проекцией на координатных осях, что означает присутствие в целевой функции переменных со степенью не большей двух. Однако, в моем случае компоненты векторов между собой «конфликтуют», что противоречит нелинейному (квадратичному) программированию. Для примера: «конфликт» может быть связан с тем, что каждый рейс имеет определенную емкость воздушного судна и больше посадочных мест на него продать невозможно. Из-за наличия «конфликтов» от варианта решения задачи нелинейным программированием пришлось отказаться в пользу все того же многокритериального программирования.
После разбора вариантов решения задачи я пошел классическим вариантом декомпозиции со следующими частями:
При этом после декомпозиции логически следовал вопрос, а собственно на основании какого подхода лучше построить транспортную маршрутную сеть? И какой из имеющихся графов более приемлем для решения данной задачи?
По классике жанра нашлась не одна, а несколько моделей, которые я и стал рассматривать.
Время-расширенный граф представляет собой ориентированный граф. Дуги такого графа — это направления пунктов отправления и прибытия рейсов, а вершины — это слоты (время взлета и посадки) рейсов. Использование время-расширенной модели заключается в расширении исходного графа с аэропортами вершинами и дугами, отражая связи маршрутов путем объединения аэропортов между собой в соответствии с расписанием рейсов:
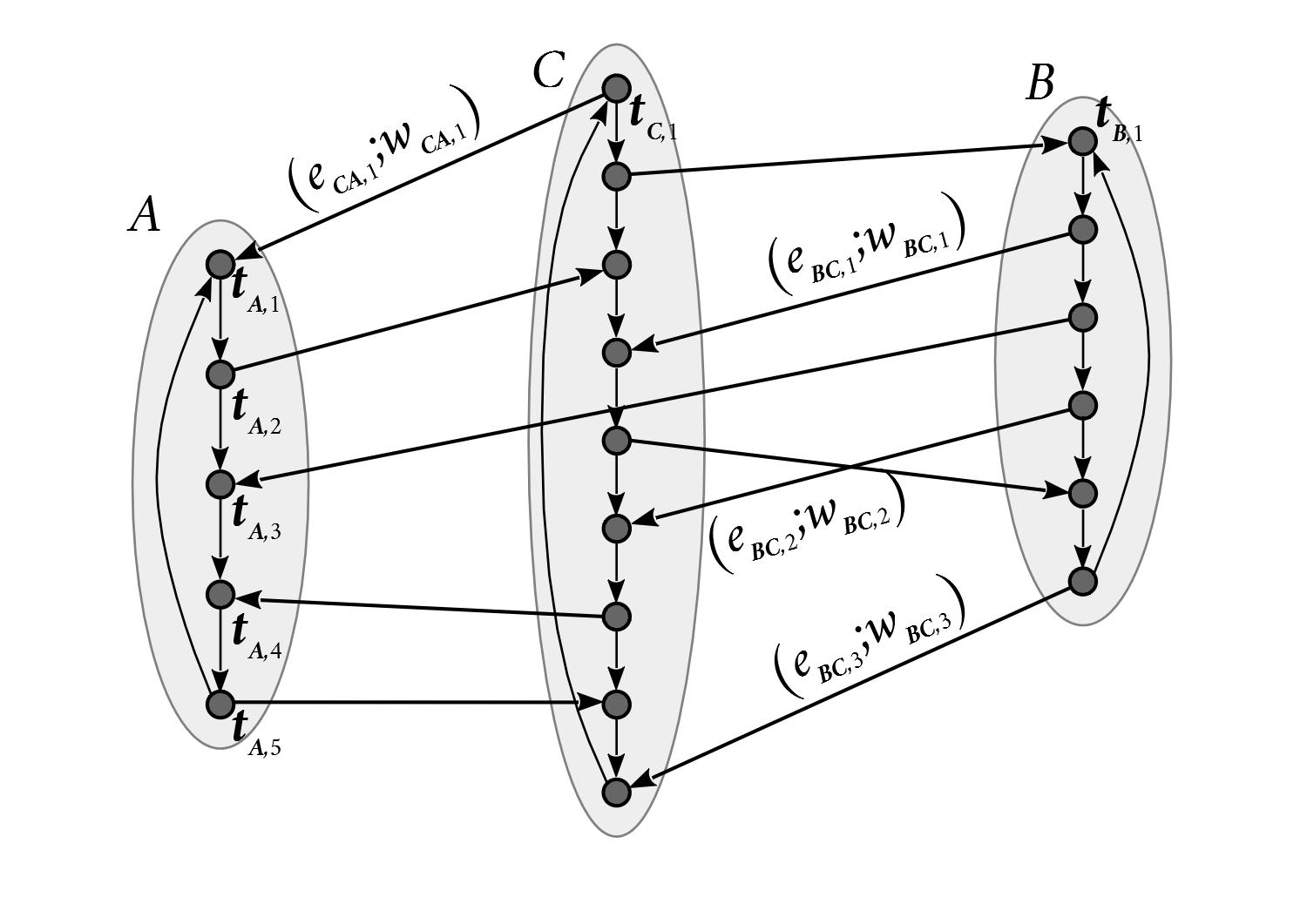
Дуги обозначены как . Например, дуга соединяет аэропорт с аэропортом и направлена от к , указанный через запятую индекс показывает, что это не единственный рейс, а третий по счету. При этом каждая дуга может быть легко взвешена, например, вес дуги может быть вычислен как . Вершины внутри отдельно взятого аэропорта легко упорядочиваются согласно временному показателю каждого рейса, и так же на основании стыковочного времени внутри аэропорта рейсы соединяются дугами, которые соответствуют доступному времени пересадки с одного рейса на другой.
Преимуществом время-расширенного графа является то, что путь наискорейшего прибытия может быть найден за минимальное время, например, с помощью алгоритма Дейкстры. Недостатком использования такого подхода является многократное увеличение вершин и ребер, что, впрочем, не влияет на разреженность графа, ведь увеличение количества ребер пропорционально увеличению количества вершин.
Время-зависимый граф представляет собой ориентированный граф без дополнительных преобразований над исходным графом. Каждой дуге соответствует маршрут со связями между аэропортами, дуга при этом обладает специальным набором данных, включающим в себя параметры о времени отправления и прибытия рейса по маршруту. Извлекаемое из этого набора данных значение зависит от того в какой именно момент времени происходит обращение к данной дуге, отсюда и название — «время-зависимый».

Преимуществом время-зависимого графа является то, что он позволяет найти путь с наименьшим количеством пересадок, недостатком является чрезмерная нагрузка данными каждой дуги.
Мультиграф представляет собой ориентированный граф с совокупностями характеристик присущих время-расширенной и время-зависимой моделям.
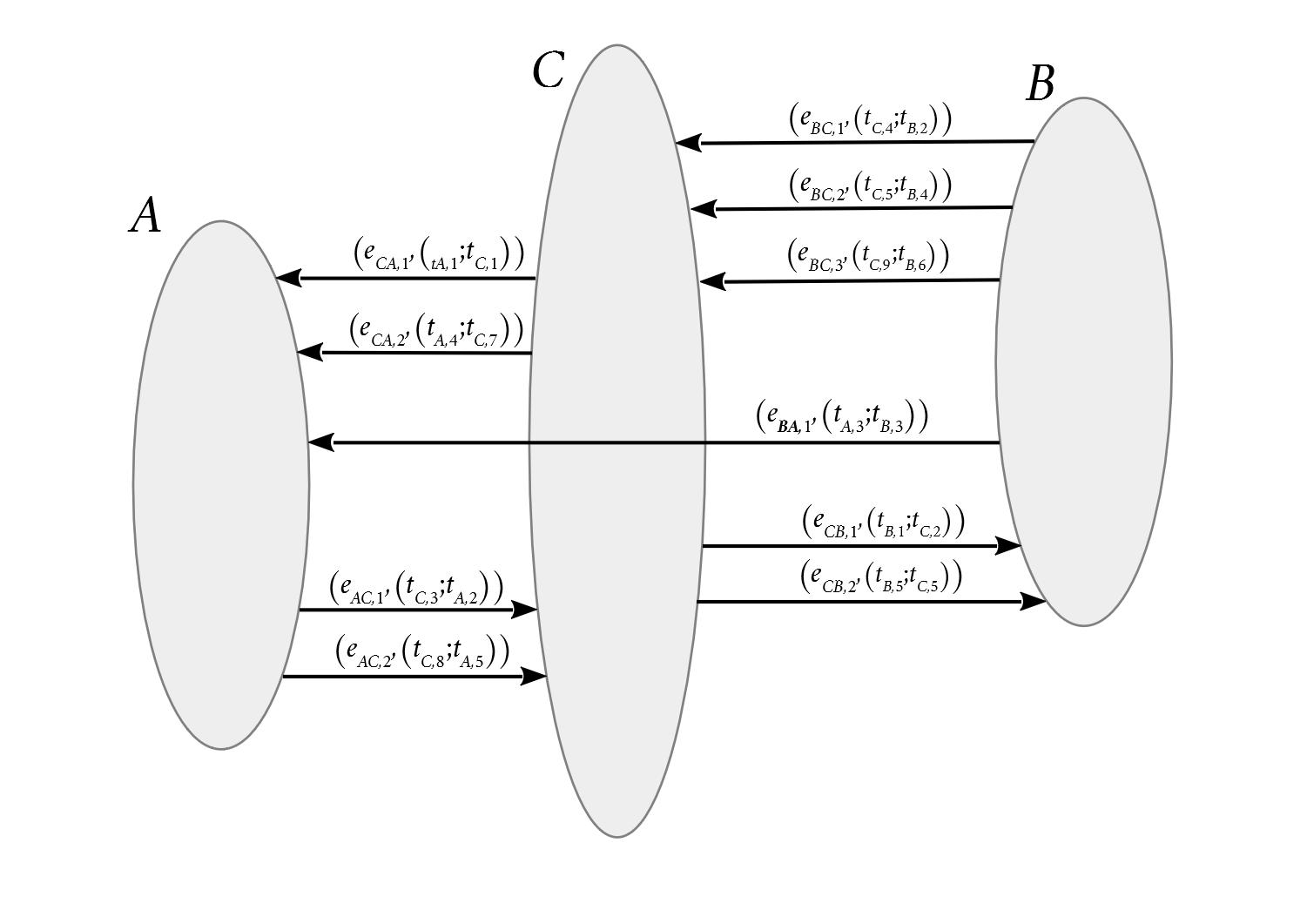
Между аэропортами находится столько же дуг сколько и во время-расширенной модели, но эти дуги «взвешены» временем вылета и прилета, при этом стыковочное время между рейсами в каждом аэропорту придется постоянно и многократно вычислять. С другой стороны, в мультиграфовом представлении ровно столько же информации о рейсах, сколько и во время-зависимой модели, но вся эта информация закреплена за множеством дуг. Поиск пути с наименьшим количеством пересадок, будет выполняться так же просто как и во время-зависимой модели, но проходя по одной дуге не учитывается информация других дуг, поэтому после того как путь с наименьшим количеством пересадок будет найден, придется повторно пройти по этому пути для вычисления информации о других рейсах (дугах).
Представление транспортной маршрутной сети в виде мультиграфа является «сырым» состоянием для время-расширенной и время-зависимой моделей. Поиск пути с наикратчайшим прибытием будет выполняться теми же самыми преобразованиями, характерными для время-расширенной модели, а поиск пути с наименьшим количеством пересадок — по время-зависимой модели. И влечет увеличение времени расчета сети. Однако, тут возникает нюанс, ведь поиск «кратчайшего» пути по двум критериям, в общем случае, уже относится к классу NP трудных задач и модификация алгоритма Дейкстры выполняет довольно сложные манипуляции с разметкой вершин.
Представление вычислительной сложности задачи с представленным мультиграфом модели множества маршрутов с аэропортами и рейсами можно рассмотреть через самый простой способ модификации — алгоритм Дейкстры, который ищет только Парето-оптимальные пути. Общая сумма критериев отдельно взятого Парето-оптимального пути не может быть хуже или лучше других Парето-оптимальных путей по всем критериям одновременно. Например, множество путей со следующей суммой двух критериев {(30, 10), (20, 20), (10, 30)} будет Парето-оптимальным.
В качестве более наглядного примера, рассмотрим работу алгоритма на небольшом графе, дуги которого взвешены двумерными векторами:

Работа модифицированного алгоритма Дейкстры на таком графе так же, как и обычного алгоритма для обычного графа, будет состоять из итераций с последовательным вычеркиванием вершин, за исключением того, что каждая вершина может обладать не одним Парето-оптимальным значением, а несколькими. Помимо этого, так же нужно сохранять информацию, о происхождении каждого вычисленного значения суммы.
Учитывая, что в задаче рассматриваются маршруты со связями аэропортов по рейсам, вполне уместно предположить, что дуг между двумя вершинами может быть довольно много, при этом каждая из них может быть взвешена, как минимум трехкомпонентным вектором. Но с увеличением компонент векторов может происходить и увеличение Парето-оптимальных путей. При этом почти все дуги между двумя вершинами могут оказаться Парето-оптимальными. В таком случае сумма путей будет содержать еще больше Парето-оптимальных путей. Это можно увидеть на небольшом мультиграфе взвешенного двумерными векторами:

Использование в такой модели модифицированного алгоритма Дейкстры допустимо, так как он может работать и на мультиграфах, но скорость отработки алгоритма зависит как от количества вершин , так и от количества дуг . Для разреженных простых графов и обычного алгоритма сложность составляет порядка . Однако, будет ли полученный мультиграф «разреженным» сказать сложно, так как в общем случае реберная плотность мультиграфов может быть гораздо больше, чем у полного графа. Если принять во внимание, что количество ребер полного графа определяется через количество его вершин по формуле:
А реберная плотность определяется как:
Для полных графов , но для мультиграфов значение реберной плотности вообще ничем не ограничено.
Поэтому я пришел к выводу, что найти кратчайший путь можно с помощью алгоритма Дейкстры, а все остальные кратчайшие пути — с помощью алгоритма Йена. Учитывая, что на этом этапе мы оперируем невзвешеными дугами и можем сразу отбрасывать пути, допустим с четырьмя пересадками, то поиск одного кратчайшего пути будет гарантированно выполняться менее чем за .

Учитывая, что данная статья не охватывает непосредственные результаты реализации, то заранее могу предположить, что модифицированный алгоритм Дейкстры на мультиграфовой модели не будет отрабатывать с учетом оптимального временного интервала.
Поэтому перейду к непосредственному решению первой подзадачи, а именно к решению вопроса, связанного с многокритериальной оптимизацией, выбранным мною методом условной оптимизации. Метод заключается в том, что несмотря на противоречивость критериев, всегда существует наиболее приоритетный, а все остальные обладают допустимыми значениями. В итоге оптимизация всей задачи сводится к оптимизации по наиболее приоритетному.
Особенностью задачи является тот факт, что в расчет входят не только прямые рейсы, что всегда значительно упрощает задачу, а наоборот, стыковочные или с пересадками. Поэтому модель время-зависимого графа как нельзя кстати подходит для решения задачи, ведь зачастую количество пересадок не формируется больше 3-4 сегментов в маршруте. Время-зависимый граф, в первую очередь, несет информацию о совокупности доступных маршрутов в виде рейсов со связями между аэропортами. Затем вычисляется оценка времени отправления и прибытия для стыковки с учетом обычного не взвешенного графа. Все, что нужно сделать на этом этапе — найти все допустимые маршруты между аэропортами «A» и «B» с заранее фиксированным количеством пересадок, например, тремя.

Учитывая, что на этом этапе граф является невзвешенным, то найти кратчайший путь можно с помощью обычного поиска в ширину, а все остальные кратчайшие пути — с помощью алгоритма Йена. Так как поиск в ширину выполняется за линейное время, то можно говорить, что время поиска всех путей, с теми же 3-мя пересадками, будет линейным.
При оценке применения алгоритмов для поиска оптимальных маршрутов и наличия данных по частоте обновления расписания можно сказать, что идея о заранее предрасчитанной матрице со всеми «кратчайшими» путями по направлениям является обоснованной. Конечно, на первоначальном этапе создания матрицы такое решение обернется трудоемкими вычислениями, но зато, в дальнейшем, позволит практически мгновенно находить «кратчайшие» пути и оперативно вносить коррективы в саму матрицу.
Однако, остается вопрос с тем, а какие «кратчайшие» пути маршрутов со стыковками и пересадками являются наиболее «кратчайшими»? В противном случае мы имеем массив данных, которые не позволят нам принять решение. Набор критериев зачастую сводится к наиболее оптимальными в данном случае, а именно:
Оба критерия могут обладать настраиваемыми интервалами или значениями времени, поэтому остается только выполнить комбинирование маршрутов и «на лету» проверить на соответствие допустимых значений:

Учитывая то, что максимальное количество пересадок варьируется в значениях 3-4-х, то некоторые комбинации рейсов сразу будут исключаться, приводя нас к решению следующей подзадачи — выявлению среди маршрутов самых «оптимальных» по разновидности критериев.
Критериальная система является основной проблемой при формировании выдачи маршрутов, ведь понятие «оптимальный» будет зависеть от предпочтений конкретного пассажира, а он зачастую только по факту получения ответа на запрос может управлять полученными маршрутами путем установления разного набора фильтров. И даже в случае предоставления ему отранжированных маршрутов в соответствии с «кратчайшими» путями, результаты выдачи будут представлять из себя массив данных, который не позволит определиться пассажиру и приведет к нескончаемому перебору вариантов. Поэтому формирование массива вариантов маршрутов, учитывающих различные комбинации применения фильтров, как в совокупности, так и по отдельности является предельно важным параметром, влияющим на всю задача.
Что же тогда необходимо учитывать и как? Создание ранжирующих фильтров — это весьма трудоемкая задача, т.к. набор фильтров, их количество и степень влияния друг на друга может существенно изменить результат поиска оптимальных путей в результате отработки поисковых алгоритмов. Тогда из чего он может состоять? Всем нам известны ключевые параметры рейса — сведения по авиакомпаниям, даты со временем вылета/прилета, аэропорты вылета/прилета, смещения часовых поясов, время по стыковкам и пересадкам, но мы зачастую забываем о таких данных как необходимое и достаточное время для прибытия в аэропорт или время движения между аэропортами для выполнения стыковки в случае когда последующий вылет осуществляется из другой точки локации. Причем мы не должны забывать о категории нашего пассажира, а также их количестве для последующего предложения не только оптимального маршрута по времени, но и по цене в зависимости от тарифной политики.
Массив предложений должен вселять определенную степень уверенности в каждого путешественника, как бы парадоксально это ни звучало. Уверенности, основанной на математических принципах и заключающейся в предоставлении минимального набора предложений с вариантами маршрутов, которые учитывают предпочтения и снижают риск возникновения форс-мажоров. И в данном случае форс-мажоры это не только вероятность задержки рейса или изменения времени и аэропорта вылета/прилета, а также, такие показатели как природные, технологенные и эпидемиологические ситуации, влекущие за собой полную или частичную отмену рейсов.
Умение управлять данными в наших реальностях влечет каждый раз за собой много вопросов: а все ли учтено, что можно добавить еще. И в этом желании построить транспортную маршрутную сеть возникает парадокс, связанный с тем, что алгоритм должен быть как оптимальным, так и простым одновременно. Но ведь зачастую приходится жертвовать чем-то, отсюда где-то минимизация первоначальных критериев до минимального количества виделась мне наиболее приемлемой.
Если идти по пути выбора критериев, то, опуская вторичные, можно выделить такие варианты, которые учитывают не только время всего пути, стоимость и комфортность, количество пересадок и их продолжительность пересадок, но и, допустим, сведения загруженности аэропортов и данные по сообщению между аэропортами при выполнении смены одного аэропорта на другой. Это обосновывается тем, что при формировании стыковок с учетом наличия в одном городе нескольких аэропортов, имеющих разное сообщение с внешними аэропортами, в расчет времени и формирования маршрута будет закладываться не только авиасообщение, но время перемещения при возникновении такой ситуации. А они имеют место быть…
Система принятия решений в выборе «оптимальных» маршрутов в ситуациях когда у нас присутствует набор критериальных множеств, влияющих на предпочтения, является как раз тем камнем преткновения, о котором на начальных этапах, я совсем и не задумывался. Даже приведя их к некой систематизации, возникает достаточно много различий в применении их друг с другом, поэтому рассмотрим их по отдельности.
Комфортность
Значение понятия «комфортность» каждый понимает по-разному, но при этом авиакомпаниями приняты следующие уровни:
В своем подходе я допустил, что параметр «комфортность» может измеряться и принимать значения от 1 до 10, и сформировал следующее условие: чем меньше этот показатель для конкретного рейса, тем менее комфортным он будет в системе ранжирования. При этом сразу возникает проблема, которая связана с неаддитивностью такой величины, т.е. сумма показателей комфортности двух рейсов не будет отражать их общую комфортность. Например, имеются две комбинации маршрутов:
По итогу сумма и среднее арифметическое значение параметра «комфортность» каждого пути будут одинаковы, но они не будут отражать истинного положения дел. Однако, учитывая необходимость рассмотрения именно совокупной комфортности двух маршрутов, целесообразнее всего в этой ситуации использовать их средние значения вместе с среднеквадратическим отклонением, которое позволило бы оценивать «разброс» уровней комфортностей. То есть при первоначальном рассмотрении мы обращаем внимание на среднюю комфортность, а затем, по величине среднеквадратического отклонения рассматриваем то, как сильно отличаются эти комфортности друг от друга. Таким образом данный критерий распадается на два очень «близких». Хотя с другой стороны, даже без кропотливой экспертизы ясно, что допущение такой «измеримости» уровня комфорта является очень далеким от реальности, ведь у нас есть заранее известные уровни классов. А во-вторых, так же очевидно, что комфортность всего пути находится в какой-то функциональной зависимости и от других критериев, например, длительности перелета, количества пересадок с их длительностью, рейтинга авиакомпании и ее воздушного парка. Имеет ли смысл ориентироваться на данный критерий — вопрос. Ведь в основе подхода лежит система учета совокупности «оптимальных» путей. Поэтому в дальнейшем будем использовать представление комфортности в виде двух показателей: среднего арифметического значения показателей комфортности рейсов и их среднеквадратичного отклонения.
Продолжительность пересадок
Существуют две разновидности согласования маршрутов:
Интересует из этого списка понятие «стыковка», которая является результатом комбинации двух или более авиакомпаний в одном маршруте с согласованными временными периодами, на основании минимального стыковочного необходимого времени, но не всегда достаточного для пересадки с одного рейса на другой. Поэтому, для комбинирования рейсов, в таком маршруте необходимо рассчитывать достаточное время, требующееся для выполнения стыковки.
Вот тут у нас возникает диссонанс, ведь зачастую такие рейсы могут исключаться из вариантов для предложения, но, в силу наличия такого критерия, бывают ситуации, когда стыковка с временным ожиданием больше суток является «оптимальной» для нашего пассажира. Поэтому имеет смысл не отбрасывать пути со слишком долгим временем пересадки, так как, пусть и редко, они все равно могут оказаться востребованы.
Загруженность аэропортов
Показатель загруженности аэропорта можно оценивать при расчете «оптимальных» путей с оценкой степени их наполнения по факту продажи билетов на рейсы с учетом участия того или иного аэропорта в маршруте. Очевидно, что в таком допущении, минимальное стыковочное время будет иметь некую функциональную зависимость от загруженности аэропорта.
Количество пересадок
Количество пересадок само по себе является противоречивой величиной. Ведь зачастую именно таким способом можно снизить стоимость всего маршрута. С другой стороны, есть категория пассажиров, которым наличие даже одной пересадки создает ряд проблем. Не стоит забывать ситуации, когда маршрут с пересадкой является наиболее «оптимальным» в силу того, что на желаемый маршрут остались дорогие билеты на бизнес-класс или, допустим, остались билеты с тарифом без возможности обмена/возврата, что влечет за собой вероятность отказа от предлагаемого варианта.
Но в количестве пересадок заложен еще один подкритерий — это вероятность перемещения из одного аэропорта в другой. Поэтому формирование стыковок зачастую является сложной задачей, ведь в расчет маршрута необходимо закладывать время на перемещение между аэропортами, а это влечет за собой необходимость заказа билетов на транспорт внутри города для осуществления перемещения в подпунктах.
Критерии «время в пути» и «стоимость» являются абсолютно аддитивными величинами, поэтому они опираются на непосредственные показатели с системой ранжирования. И все бы ничего, если бы не необходимость включения общего времени в пути с расчетом времени для прибытия в аэропорт или отправления из него в пункт назначения, а также при стыковках учета необходимости дополнительных трат на перемещение между аэропортами. На данном этапе позволю себе пренебречь этим уточнением.
Предположим, что определение «оптимальность» должно пониматься, как самое лучшее всегда и для всех и при этом не только для пассажиров, но и для авиакомпаний, аэропортов и, может быть в последствии, других поставщиков трэвел-услуг.
В этом случае, разбиение единой, очень сложной цели на подцели является единственным выходом. Подобное разбиение может выглядеть вот так:

Совершенно очевидно, что для того что бы удовлетворить все области заинтересованности, придется достигнуть менее «глобальных», но в какой-то степени противоречащих друг другу целей. Как этого добиться? Пожалуй это отличная тема для другой статьи. Но забегая вперед, можно сказать, что разбиение сложной цели на более простые подцели так же связано с оптимизацией и теорией графов, а именно поиском оптимальных иерархических структур.
Система принятия решений довольно тесно связана с такими методами, как критерии Лапласа, Вальда, Сэвиджа и Гурвица, поэтому, обладая массивом «кратчайших» маршрутов, я не мог не узнать какие из них окажутся самыми «оптимальными» на их основе.
Одним из самых универсальных подходов в решении задач многоцелевой оптимизации является поиск оптимальных решений по Парето и Слейтеру. Если оценивать массив «кратчайших» маршрутов по критерию оптимальности Слейтера, то оптимальным будет считаться такой путь, который является самым лучшим по всем критериям одновременно. Путь считается оптимальным по Парето, если все остальные пути являются лучше него по какому-то одному параметру, но хуже по другому, т.е. нельзя улучшить путь хотя бы по одному критерию, не ухудшив его по остальным.
Все решения оптимальности по Парето и по Слейтеру можно легко продемонстрировать графически, для задачи минимизации с двумя критериями:
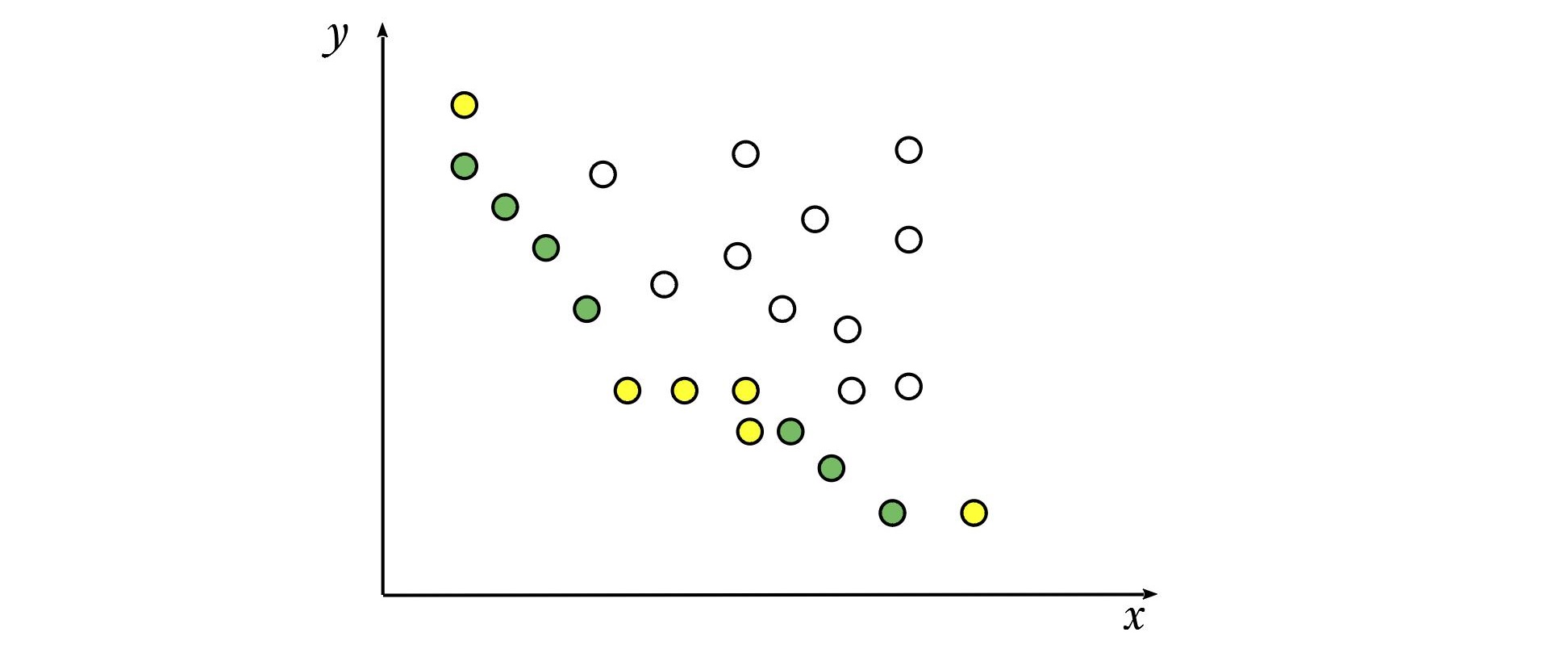
Множество точек с параметрами критериев оптимальных по Парето обозначены зеленым цветом, а оптимальные по Слейтеру обозначены желтым. Множество точек оптимальных по Cлейтеру так же содержит множество точек оптимальных по Паретто. В рамках рассматриваемой задачи, все эти точки будут представлять собой концы векторов, начинающихся в начале координат семимерного пространства.
В заключение могу сказать, что это лишь вершина айсберга, которая позволяет дать начальное представление с чем сталкиваются поисковые системы при формировании оптимальных маршрутов.
Как часто случается, далеко не всегда в ответ на запрос с поиском маршрута выдается желанный результат с рейсом, который сразу же идет на оформление заказа. Мы начинаем переходить с сайта на сайт, чтобы получить удовлетворяющий ответ.
Возникновение похожих случаев сопряжено с отсутствием прямого сообщения или заранее предусмотренных комбинированных (стыковочных) маршрутов, либо предлагались маршруты с пересадками, которые включали время ожидания следующего рейса более чем 5-6 часов, а то и целые сутки.
Как же так получается, что при всем многообразии авиакомпаний мы получаем ответы, далеко не всегда нас удовлетворяющие, и вообще, как алгоритмически строятся механизмы поиска вариантов маршрутов? В этом вопросе нам на помощь приходит прикладная математика с применением алгоритмов и критериями оценки.

Карта аэропортов мира
Решением логистических задач я занимаюсь довольно давно и когда столкнулся с задачей построения поисковой системы, которая будет искать оптимальные маршруты, мне она показалась довольно тривиальной. По опыту я мог заранее сказать, что ее можно решить довольно простыми методами и в сравнительно короткие сроки. Однако, если бы все было так просто, то данная статья бы и не появилась. Поэтому, включившись в работу, через некоторое время я понял, что не такая уж она и тривиальная.
Отправной точкой, как часто это бывает в путешествиях, а именно с таким подходом я и подошел, стало решение построить транспортную сеть в виде графа. Транспортная сеть изначально включала данные по аэропортам, авиакомпаниям, их расписанию с рейсами и показатели стыковочного времени.
За основу было принято, что в качестве вершины графа рассматриваются аэропорты, а ребрами являются рейсы между ними. В результате у нас получился костяк, как в скелете, на основании которого начал накладывать расписание, которое имело свои характеристики: время отправления и прибытия. При этом движение по ребрам всегда возможно только в определенное время, что характеризуется частными вариантами решения задачи:
- минимальное время в пути;
- минимальное (или простым языком адекватное) число пересадок;
- временной интервал для осуществления пересадки с одного рейса на другой при выборе сложных маршрутов.
Сложность при этом заключается в том, что ни при каких условиях у нас нет применения только одного частного случая, запрос всегда содержит связанные между собой критерии поиска, включающие в себя один-два или более уточнений. Отсюда вытекает, что применение критериальности накладывает определенные условия на расчет искомых вариантов маршрутов. Помимо трех перечисленных выше, в расчет закладывается применение категорий классов обслуживания (первый, бизнес, эконом), стоимость, количество пассажиров и их категории, а также наличие целого ряда дополнительных услуг, влияющих на результат. Таким образом это полностью стало укладываться в мою концепцию решения задачи путем многокритериальной оптимизации (многоцелевая оптимизация), а именно — поиска кратчайшего пути по нескольким критериям (MOSP — multi-objective shortest path).
Но, как всем известно, для того, чтобы проверить одну гипотезу, надо привести ряд других. В качестве еще одного варианта решения задачи рассматривалось применение нелинейного программирования.
Учитывая, что дуги графа взвешены векторами, решение задачи можно было свести к квадратичному (нелинейному) программированию. И все бы было идеально, если бы не тот факт, что вектора, по сути, обладают всего двумя характеристиками: длиной и проекцией на координатных осях, что означает присутствие в целевой функции переменных со степенью не большей двух. Однако, в моем случае компоненты векторов между собой «конфликтуют», что противоречит нелинейному (квадратичному) программированию. Для примера: «конфликт» может быть связан с тем, что каждый рейс имеет определенную емкость воздушного судна и больше посадочных мест на него продать невозможно. Из-за наличия «конфликтов» от варианта решения задачи нелинейным программированием пришлось отказаться в пользу все того же многокритериального программирования.
После разбора вариантов решения задачи я пошел классическим вариантом декомпозиции со следующими частями:
- поиск на основе расписания всех «кратчайших» путей из точки отправления в точку прибытия;
- поиск среди «кратчайших» путей самого «оптимального» на основании критериальности.
При этом после декомпозиции логически следовал вопрос, а собственно на основании какого подхода лучше построить транспортную маршрутную сеть? И какой из имеющихся графов более приемлем для решения данной задачи?
По классике жанра нашлась не одна, а несколько моделей, которые я и стал рассматривать.
Время-расширенная модель
Время-расширенный граф представляет собой ориентированный граф. Дуги такого графа — это направления пунктов отправления и прибытия рейсов, а вершины — это слоты (время взлета и посадки) рейсов. Использование время-расширенной модели заключается в расширении исходного графа с аэропортами вершинами и дугами, отражая связи маршрутов путем объединения аэропортов между собой в соответствии с расписанием рейсов:

Дуги обозначены как . Например, дуга соединяет аэропорт с аэропортом и направлена от к , указанный через запятую индекс показывает, что это не единственный рейс, а третий по счету. При этом каждая дуга может быть легко взвешена, например, вес дуги может быть вычислен как . Вершины внутри отдельно взятого аэропорта легко упорядочиваются согласно временному показателю каждого рейса, и так же на основании стыковочного времени внутри аэропорта рейсы соединяются дугами, которые соответствуют доступному времени пересадки с одного рейса на другой.
Преимуществом время-расширенного графа является то, что путь наискорейшего прибытия может быть найден за минимальное время, например, с помощью алгоритма Дейкстры. Недостатком использования такого подхода является многократное увеличение вершин и ребер, что, впрочем, не влияет на разреженность графа, ведь увеличение количества ребер пропорционально увеличению количества вершин.
Время-зависимая модель
Время-зависимый граф представляет собой ориентированный граф без дополнительных преобразований над исходным графом. Каждой дуге соответствует маршрут со связями между аэропортами, дуга при этом обладает специальным набором данных, включающим в себя параметры о времени отправления и прибытия рейса по маршруту. Извлекаемое из этого набора данных значение зависит от того в какой именно момент времени происходит обращение к данной дуге, отсюда и название — «время-зависимый».

Преимуществом время-зависимого графа является то, что он позволяет найти путь с наименьшим количеством пересадок, недостатком является чрезмерная нагрузка данными каждой дуги.
Мультиграф
Мультиграф представляет собой ориентированный граф с совокупностями характеристик присущих время-расширенной и время-зависимой моделям.

Между аэропортами находится столько же дуг сколько и во время-расширенной модели, но эти дуги «взвешены» временем вылета и прилета, при этом стыковочное время между рейсами в каждом аэропорту придется постоянно и многократно вычислять. С другой стороны, в мультиграфовом представлении ровно столько же информации о рейсах, сколько и во время-зависимой модели, но вся эта информация закреплена за множеством дуг. Поиск пути с наименьшим количеством пересадок, будет выполняться так же просто как и во время-зависимой модели, но проходя по одной дуге не учитывается информация других дуг, поэтому после того как путь с наименьшим количеством пересадок будет найден, придется повторно пройти по этому пути для вычисления информации о других рейсах (дугах).
Представление транспортной маршрутной сети в виде мультиграфа является «сырым» состоянием для время-расширенной и время-зависимой моделей. Поиск пути с наикратчайшим прибытием будет выполняться теми же самыми преобразованиями, характерными для время-расширенной модели, а поиск пути с наименьшим количеством пересадок — по время-зависимой модели. И влечет увеличение времени расчета сети. Однако, тут возникает нюанс, ведь поиск «кратчайшего» пути по двум критериям, в общем случае, уже относится к классу NP трудных задач и модификация алгоритма Дейкстры выполняет довольно сложные манипуляции с разметкой вершин.
Представление вычислительной сложности задачи с представленным мультиграфом модели множества маршрутов с аэропортами и рейсами можно рассмотреть через самый простой способ модификации — алгоритм Дейкстры, который ищет только Парето-оптимальные пути. Общая сумма критериев отдельно взятого Парето-оптимального пути не может быть хуже или лучше других Парето-оптимальных путей по всем критериям одновременно. Например, множество путей со следующей суммой двух критериев {(30, 10), (20, 20), (10, 30)} будет Парето-оптимальным.
В качестве более наглядного примера, рассмотрим работу алгоритма на небольшом графе, дуги которого взвешены двумерными векторами:

Работа модифицированного алгоритма Дейкстры на таком графе так же, как и обычного алгоритма для обычного графа, будет состоять из итераций с последовательным вычеркиванием вершин, за исключением того, что каждая вершина может обладать не одним Парето-оптимальным значением, а несколькими. Помимо этого, так же нужно сохранять информацию, о происхождении каждого вычисленного значения суммы.
Учитывая, что в задаче рассматриваются маршруты со связями аэропортов по рейсам, вполне уместно предположить, что дуг между двумя вершинами может быть довольно много, при этом каждая из них может быть взвешена, как минимум трехкомпонентным вектором. Но с увеличением компонент векторов может происходить и увеличение Парето-оптимальных путей. При этом почти все дуги между двумя вершинами могут оказаться Парето-оптимальными. В таком случае сумма путей будет содержать еще больше Парето-оптимальных путей. Это можно увидеть на небольшом мультиграфе взвешенного двумерными векторами:

Использование в такой модели модифицированного алгоритма Дейкстры допустимо, так как он может работать и на мультиграфах, но скорость отработки алгоритма зависит как от количества вершин , так и от количества дуг . Для разреженных простых графов и обычного алгоритма сложность составляет порядка . Однако, будет ли полученный мультиграф «разреженным» сказать сложно, так как в общем случае реберная плотность мультиграфов может быть гораздо больше, чем у полного графа. Если принять во внимание, что количество ребер полного графа определяется через количество его вершин по формуле:
А реберная плотность определяется как:
Для полных графов , но для мультиграфов значение реберной плотности вообще ничем не ограничено.
Поэтому я пришел к выводу, что найти кратчайший путь можно с помощью алгоритма Дейкстры, а все остальные кратчайшие пути — с помощью алгоритма Йена. Учитывая, что на этом этапе мы оперируем невзвешеными дугами и можем сразу отбрасывать пути, допустим с четырьмя пересадками, то поиск одного кратчайшего пути будет гарантированно выполняться менее чем за .

Учитывая, что данная статья не охватывает непосредственные результаты реализации, то заранее могу предположить, что модифицированный алгоритм Дейкстры на мультиграфовой модели не будет отрабатывать с учетом оптимального временного интервала.
Поэтому перейду к непосредственному решению первой подзадачи, а именно к решению вопроса, связанного с многокритериальной оптимизацией, выбранным мною методом условной оптимизации. Метод заключается в том, что несмотря на противоречивость критериев, всегда существует наиболее приоритетный, а все остальные обладают допустимыми значениями. В итоге оптимизация всей задачи сводится к оптимизации по наиболее приоритетному.
Особенностью задачи является тот факт, что в расчет входят не только прямые рейсы, что всегда значительно упрощает задачу, а наоборот, стыковочные или с пересадками. Поэтому модель время-зависимого графа как нельзя кстати подходит для решения задачи, ведь зачастую количество пересадок не формируется больше 3-4 сегментов в маршруте. Время-зависимый граф, в первую очередь, несет информацию о совокупности доступных маршрутов в виде рейсов со связями между аэропортами. Затем вычисляется оценка времени отправления и прибытия для стыковки с учетом обычного не взвешенного графа. Все, что нужно сделать на этом этапе — найти все допустимые маршруты между аэропортами «A» и «B» с заранее фиксированным количеством пересадок, например, тремя.

Учитывая, что на этом этапе граф является невзвешенным, то найти кратчайший путь можно с помощью обычного поиска в ширину, а все остальные кратчайшие пути — с помощью алгоритма Йена. Так как поиск в ширину выполняется за линейное время, то можно говорить, что время поиска всех путей, с теми же 3-мя пересадками, будет линейным.
При оценке применения алгоритмов для поиска оптимальных маршрутов и наличия данных по частоте обновления расписания можно сказать, что идея о заранее предрасчитанной матрице со всеми «кратчайшими» путями по направлениям является обоснованной. Конечно, на первоначальном этапе создания матрицы такое решение обернется трудоемкими вычислениями, но зато, в дальнейшем, позволит практически мгновенно находить «кратчайшие» пути и оперативно вносить коррективы в саму матрицу.
Однако, остается вопрос с тем, а какие «кратчайшие» пути маршрутов со стыковками и пересадками являются наиболее «кратчайшими»? В противном случае мы имеем массив данных, которые не позволят нам принять решение. Набор критериев зачастую сводится к наиболее оптимальными в данном случае, а именно:
- минимальное время в пути;
- минимальное число пересадок.
Оба критерия могут обладать настраиваемыми интервалами или значениями времени, поэтому остается только выполнить комбинирование маршрутов и «на лету» проверить на соответствие допустимых значений:

Учитывая то, что максимальное количество пересадок варьируется в значениях 3-4-х, то некоторые комбинации рейсов сразу будут исключаться, приводя нас к решению следующей подзадачи — выявлению среди маршрутов самых «оптимальных» по разновидности критериев.
Критериальная система является основной проблемой при формировании выдачи маршрутов, ведь понятие «оптимальный» будет зависеть от предпочтений конкретного пассажира, а он зачастую только по факту получения ответа на запрос может управлять полученными маршрутами путем установления разного набора фильтров. И даже в случае предоставления ему отранжированных маршрутов в соответствии с «кратчайшими» путями, результаты выдачи будут представлять из себя массив данных, который не позволит определиться пассажиру и приведет к нескончаемому перебору вариантов. Поэтому формирование массива вариантов маршрутов, учитывающих различные комбинации применения фильтров, как в совокупности, так и по отдельности является предельно важным параметром, влияющим на всю задача.
Что же тогда необходимо учитывать и как? Создание ранжирующих фильтров — это весьма трудоемкая задача, т.к. набор фильтров, их количество и степень влияния друг на друга может существенно изменить результат поиска оптимальных путей в результате отработки поисковых алгоритмов. Тогда из чего он может состоять? Всем нам известны ключевые параметры рейса — сведения по авиакомпаниям, даты со временем вылета/прилета, аэропорты вылета/прилета, смещения часовых поясов, время по стыковкам и пересадкам, но мы зачастую забываем о таких данных как необходимое и достаточное время для прибытия в аэропорт или время движения между аэропортами для выполнения стыковки в случае когда последующий вылет осуществляется из другой точки локации. Причем мы не должны забывать о категории нашего пассажира, а также их количестве для последующего предложения не только оптимального маршрута по времени, но и по цене в зависимости от тарифной политики.
Массив предложений должен вселять определенную степень уверенности в каждого путешественника, как бы парадоксально это ни звучало. Уверенности, основанной на математических принципах и заключающейся в предоставлении минимального набора предложений с вариантами маршрутов, которые учитывают предпочтения и снижают риск возникновения форс-мажоров. И в данном случае форс-мажоры это не только вероятность задержки рейса или изменения времени и аэропорта вылета/прилета, а также, такие показатели как природные, технологенные и эпидемиологические ситуации, влекущие за собой полную или частичную отмену рейсов.
Умение управлять данными в наших реальностях влечет каждый раз за собой много вопросов: а все ли учтено, что можно добавить еще. И в этом желании построить транспортную маршрутную сеть возникает парадокс, связанный с тем, что алгоритм должен быть как оптимальным, так и простым одновременно. Но ведь зачастую приходится жертвовать чем-то, отсюда где-то минимизация первоначальных критериев до минимального количества виделась мне наиболее приемлемой.
Если идти по пути выбора критериев, то, опуская вторичные, можно выделить такие варианты, которые учитывают не только время всего пути, стоимость и комфортность, количество пересадок и их продолжительность пересадок, но и, допустим, сведения загруженности аэропортов и данные по сообщению между аэропортами при выполнении смены одного аэропорта на другой. Это обосновывается тем, что при формировании стыковок с учетом наличия в одном городе нескольких аэропортов, имеющих разное сообщение с внешними аэропортами, в расчет времени и формирования маршрута будет закладываться не только авиасообщение, но время перемещения при возникновении такой ситуации. А они имеют место быть…
Система принятия решений в выборе «оптимальных» маршрутов в ситуациях когда у нас присутствует набор критериальных множеств, влияющих на предпочтения, является как раз тем камнем преткновения, о котором на начальных этапах, я совсем и не задумывался. Даже приведя их к некой систематизации, возникает достаточно много различий в применении их друг с другом, поэтому рассмотрим их по отдельности.
Комфортность
Значение понятия «комфортность» каждый понимает по-разному, но при этом авиакомпаниями приняты следующие уровни:
- первый класс;
- бизнес класс;
- эконом класс.
В своем подходе я допустил, что параметр «комфортность» может измеряться и принимать значения от 1 до 10, и сформировал следующее условие: чем меньше этот показатель для конкретного рейса, тем менее комфортным он будет в системе ранжирования. При этом сразу возникает проблема, которая связана с неаддитивностью такой величины, т.е. сумма показателей комфортности двух рейсов не будет отражать их общую комфортность. Например, имеются две комбинации маршрутов:
- первый маршрут с двумя сегментами, первый рейд с комфортностью 10, второй с комфортностью 1;
- второй маршрут с двумя сегментами, первый рейд с комфортностью 6, второй с комфортностью 5.
По итогу сумма и среднее арифметическое значение параметра «комфортность» каждого пути будут одинаковы, но они не будут отражать истинного положения дел. Однако, учитывая необходимость рассмотрения именно совокупной комфортности двух маршрутов, целесообразнее всего в этой ситуации использовать их средние значения вместе с среднеквадратическим отклонением, которое позволило бы оценивать «разброс» уровней комфортностей. То есть при первоначальном рассмотрении мы обращаем внимание на среднюю комфортность, а затем, по величине среднеквадратического отклонения рассматриваем то, как сильно отличаются эти комфортности друг от друга. Таким образом данный критерий распадается на два очень «близких». Хотя с другой стороны, даже без кропотливой экспертизы ясно, что допущение такой «измеримости» уровня комфорта является очень далеким от реальности, ведь у нас есть заранее известные уровни классов. А во-вторых, так же очевидно, что комфортность всего пути находится в какой-то функциональной зависимости и от других критериев, например, длительности перелета, количества пересадок с их длительностью, рейтинга авиакомпании и ее воздушного парка. Имеет ли смысл ориентироваться на данный критерий — вопрос. Ведь в основе подхода лежит система учета совокупности «оптимальных» путей. Поэтому в дальнейшем будем использовать представление комфортности в виде двух показателей: среднего арифметического значения показателей комфортности рейсов и их среднеквадратичного отклонения.
Продолжительность пересадок
Существуют две разновидности согласования маршрутов:
- пересадки (заранее согласованные между авиакомпаниями);
- стыковки.
Интересует из этого списка понятие «стыковка», которая является результатом комбинации двух или более авиакомпаний в одном маршруте с согласованными временными периодами, на основании минимального стыковочного необходимого времени, но не всегда достаточного для пересадки с одного рейса на другой. Поэтому, для комбинирования рейсов, в таком маршруте необходимо рассчитывать достаточное время, требующееся для выполнения стыковки.
Вот тут у нас возникает диссонанс, ведь зачастую такие рейсы могут исключаться из вариантов для предложения, но, в силу наличия такого критерия, бывают ситуации, когда стыковка с временным ожиданием больше суток является «оптимальной» для нашего пассажира. Поэтому имеет смысл не отбрасывать пути со слишком долгим временем пересадки, так как, пусть и редко, они все равно могут оказаться востребованы.
Загруженность аэропортов
Показатель загруженности аэропорта можно оценивать при расчете «оптимальных» путей с оценкой степени их наполнения по факту продажи билетов на рейсы с учетом участия того или иного аэропорта в маршруте. Очевидно, что в таком допущении, минимальное стыковочное время будет иметь некую функциональную зависимость от загруженности аэропорта.
Количество пересадок
Количество пересадок само по себе является противоречивой величиной. Ведь зачастую именно таким способом можно снизить стоимость всего маршрута. С другой стороны, есть категория пассажиров, которым наличие даже одной пересадки создает ряд проблем. Не стоит забывать ситуации, когда маршрут с пересадкой является наиболее «оптимальным» в силу того, что на желаемый маршрут остались дорогие билеты на бизнес-класс или, допустим, остались билеты с тарифом без возможности обмена/возврата, что влечет за собой вероятность отказа от предлагаемого варианта.
Но в количестве пересадок заложен еще один подкритерий — это вероятность перемещения из одного аэропорта в другой. Поэтому формирование стыковок зачастую является сложной задачей, ведь в расчет маршрута необходимо закладывать время на перемещение между аэропортами, а это влечет за собой необходимость заказа билетов на транспорт внутри города для осуществления перемещения в подпунктах.
Критерии «время в пути» и «стоимость» являются абсолютно аддитивными величинами, поэтому они опираются на непосредственные показатели с системой ранжирования. И все бы ничего, если бы не необходимость включения общего времени в пути с расчетом времени для прибытия в аэропорт или отправления из него в пункт назначения, а также при стыковках учета необходимости дополнительных трат на перемещение между аэропортами. На данном этапе позволю себе пренебречь этим уточнением.
Иерархическая структура глобальной цели
Предположим, что определение «оптимальность» должно пониматься, как самое лучшее всегда и для всех и при этом не только для пассажиров, но и для авиакомпаний, аэропортов и, может быть в последствии, других поставщиков трэвел-услуг.
В этом случае, разбиение единой, очень сложной цели на подцели является единственным выходом. Подобное разбиение может выглядеть вот так:

Совершенно очевидно, что для того что бы удовлетворить все области заинтересованности, придется достигнуть менее «глобальных», но в какой-то степени противоречащих друг другу целей. Как этого добиться? Пожалуй это отличная тема для другой статьи. Но забегая вперед, можно сказать, что разбиение сложной цели на более простые подцели так же связано с оптимизацией и теорией графов, а именно поиском оптимальных иерархических структур.
Система принятия решений довольно тесно связана с такими методами, как критерии Лапласа, Вальда, Сэвиджа и Гурвица, поэтому, обладая массивом «кратчайших» маршрутов, я не мог не узнать какие из них окажутся самыми «оптимальными» на их основе.
Одним из самых универсальных подходов в решении задач многоцелевой оптимизации является поиск оптимальных решений по Парето и Слейтеру. Если оценивать массив «кратчайших» маршрутов по критерию оптимальности Слейтера, то оптимальным будет считаться такой путь, который является самым лучшим по всем критериям одновременно. Путь считается оптимальным по Парето, если все остальные пути являются лучше него по какому-то одному параметру, но хуже по другому, т.е. нельзя улучшить путь хотя бы по одному критерию, не ухудшив его по остальным.
Все решения оптимальности по Парето и по Слейтеру можно легко продемонстрировать графически, для задачи минимизации с двумя критериями:

Множество точек с параметрами критериев оптимальных по Парето обозначены зеленым цветом, а оптимальные по Слейтеру обозначены желтым. Множество точек оптимальных по Cлейтеру так же содержит множество точек оптимальных по Паретто. В рамках рассматриваемой задачи, все эти точки будут представлять собой концы векторов, начинающихся в начале координат семимерного пространства.
В заключение могу сказать, что это лишь вершина айсберга, которая позволяет дать начальное представление с чем сталкиваются поисковые системы при формировании оптимальных маршрутов.

