08.04.2020 11:11
Barrayar 0 1500 Источник


Эта статья представляет собой практическое, прикладное сравнение. В ней не объясняются все подробности дифференциальной приватности. Если хотите изучить этот вопрос глубже, обратитесь к ссылкам в конце статьи.

Обещание дифференциальной приватности (точнее, ?-дифференциальная приватность) — заключается в том, чтобы предоставить измеряемый способ обеспечения баланса между приватностью и точностью данных при выкладывании в публичный доступ агрегированных данных в приватных датасетах.

Допустим, у вас есть ползунок настройки:

  • уводите его влево — сохраняете полную приватность людей, чьи данные попали в датасет, но при этом добавляете в информацию большое количество шума, снижая точность совокупной статистики;
  • уводите вправо — получаете идеальную точность совокупной статистики, но раскрываете приватную информацию о людях из датасета.

Суть в том, что ползунок можно переводить в любую точку шкалы, подбирая баланс под конкретный сценарий использования.

Как преобразуются данные


?-дифференциальная приватность позволяет находить баланс между приватностью и точностью с помощью положительного значения ? (эпсилон). Если ? невелик, то мы сохраняем больше приватности, но ухудшаем точность. Если ? большой, то приватность страдает в угоду точности. Значение ? меняется от 0 до бесконечности.

В библиотеках дифференциальной приватности реализуются разные методики, берущие параметр эпсилон в качестве входного значения и добавляют к значениям в исходном датасете случайный шум, обратно пропорциональный ?. То есть чем меньше эпсилон, тем больше добавляется шума.

В некоторых библиотеках используются дополнительные параметры и предлагаются средства управления случайным шумом, например, плотность вероятности, из которой берутся случайные числа (распределение Лапласа, нормальное распределение и т. д.).

В каких-то библиотеках также реализована концепция бюджета приватности (privacy budget): при каждом вызове функции в библиотеке используется заданное пользователем количество заранее выделенного бюджета. Теоретическая основа такова: при каждой публикации новых данных возрастает вероятность того, что злоумышленник извлечёт информацию о людях из датасета. А с помощью бюджета приватности библиотека может вернуть ошибку вместо значения.

Сравнение библиотек дифференциальной приватности


Сравним три библиотеки и их работу с заданным датасетом, применив одинаковые методики:


Мы посмотрим, как влияет на точность размер датасета и желаемый уровень приватности (эпсилон). В каждом случае мы будем сравнивать полученные на разных библиотеках результаты.

Тестовый датасет


Сгенерируем случайным образом датасет, содержащий колонку с весами людей в килограммах. Будем считать эту информацию конфиденциальной, её нужно сохранить в секрете. Каждый вес представлен в виде вещественного числа двойной точности (double value).

Веса были сгенерированы в соответствии с нормальным распределением, при котором средний вес в датасете равен 70 кг, а стандартное отклонение равно 30.

Для целей исследования сделаем так, чтобы можно было генерировать датасеты разного размера.

Вот код генерирования весов:

import random

def generate_weight_dataset(dataset_size):
    outpath = f"weights_{dataset_size}.csv"
    mu = 70  # mean
    sigma = 30  # standard deviation
    with open(outpath, "w+") as fout:
        for i in range(dataset_size):
            random_weight = random.normalvariate(mu, sigma)  # normal distribution
            random_weight = abs(random_weight)  # make sure weights are positive
            random_weight = round(random_weight, 1)  # round to 1 decimal digit
            line = f"{random_weight}"
            print(line, file=fout)

Для датасета размером 10 600 сгенерированные данные будут выглядеть так:


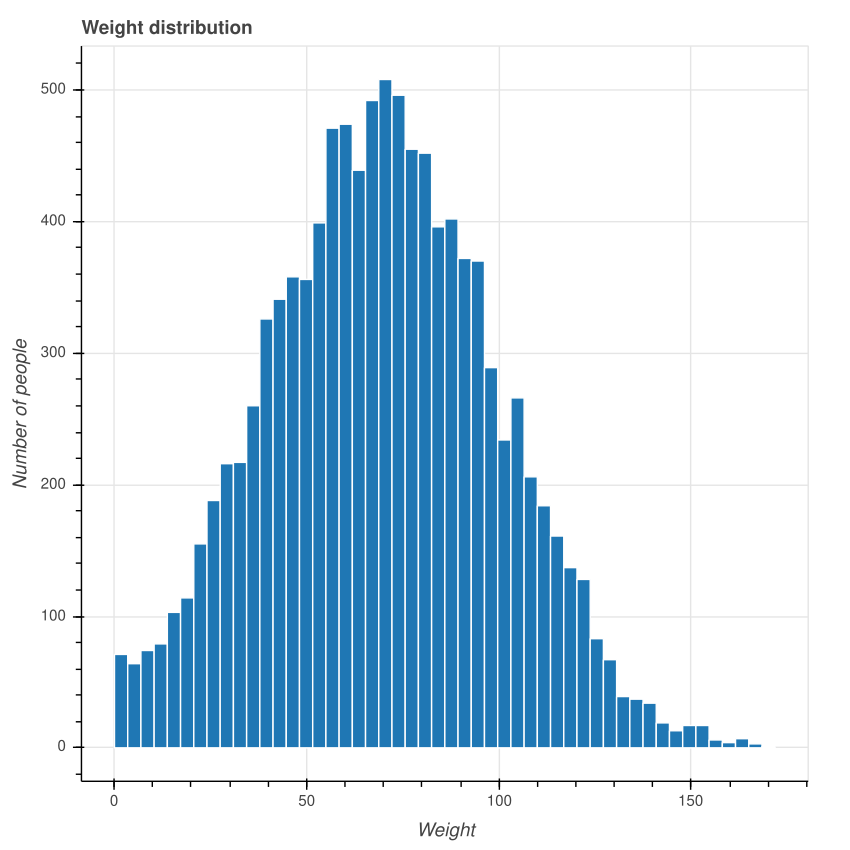
Фактическое среднее значение должно быть около 70, потому что мы использовали нормальное распределение с mean=70. Однако это не точное значение, потому что веса сгенерированы случайным образом. Кроме того, в нашем датасете отсутствуют отрицательные значения весов, а финальные значения округлены до одной цифры после запятой. В данном случае фактическое среднее значение было 70,34812570579449, а стандартное отклонение 29,488380395675765.

Обратите внимание, всё это мы сделали только для того, чтобы датасет выглядел как набор настоящих данных. Распределение значений не повлияет на оценки, которые мы будем обсуждать.

Использование библиотек


Давайте рассмотрим способ использования библиотек. Мы всегда будем сравнивать их, применяя одинаковые параметры. К примеру, во всех случаях будет одно и то же входное значение эпсилон. Для проведения измерений мы будем использовать среднее значение датасета. Все рассматриваемые библиотеки реализуют такие операции, как среднее, отклонение, сумма и прочие с применением механизмов добавления случайного шума. Часто используется механизм Лапласа. Операция поиска среднего значения выбирается произвольно, она позволяет нам протестировать все операции, использующие одинаковый механизм.

Вычислим среднее значение дифференциальной приватности с помощью библиотеки IBM (Python):

import diffprivlib.tools.utils

def dp_mean(weights, epsilon, upper):
    dp_mean = diffprivlib.tools.utils.mean(weights, epsilon=epsilon, range=upper)
    return dp_mean

upper = max(weights)
epsilon = 1.0
dpm = dp_mean(weights, epsilon, upper)

То же самое с помощью библиотеки Google (C++):

double dp_mean(std::list<double> weights, double epsilon, double lower, double upper) {
    std::unique_ptr<differential_privacy::BoundedMean<double>> mean_algorithm = 
    differential_privacy::BoundedMean<double>::Builder()
    .SetEpsilon(epsilon)
    .SetLower(0.0)
    .SetUpper(upper)
    .Build()
    .ValueOrDie();

    for (auto weight : weights) {
        mean_algorithm->AddEntry(weight);
    }
    double privacy_budget = 1.0;
    auto output = mean_algorithm->PartialResult(privacy_budget).ValueOrDie();
    return differential_privacy::GetValue<double>(output);
}

Обратите внимание, что мы используем весь бюджет приватности в размере 1,0 при каждом применении библиотеки Google. А библиотека IBM не принимает на вход этот параметр.

Теперь вычислим среднее значение ДП с помощью diffpriv (язык R):

library(diffpriv)

dp_mean <- function(xs, epsilon) {
  ## a target function we'd like to run on private data X, releasing the result
  target <- function(X) mean(X)

  ## target seeks to release a numeric, so we'll use the Laplace mechanism---a
  ## standard generic mechanism for privatizing numeric responses
  n <- length(xs)
  mech <- DPMechLaplace(target = target, sensitivity = 1/n, dims = 1)

  r <- releaseResponse(mech, privacyParams = DPParamsEps(epsilon = epsilon), X = xs)
  r$response
}

Как приватность влияет на точность


Точность среднего значения можно измерить с помощью простого вычисления разницы между средним ДП и фактическим средним.

Давайте посмотрим, что происходит с точностью среднего значения веса при изменении эпсилона. Поскольку мы добавляем случайный шум, то выполним 100 прогонов и вычислим среднеквадратичную ошибку, чтобы проверить, не генерирует ли библиотека искажённые значения.

Результат должен продемонстрировать, что ошибка (разница между фактическим средним и средним ДП) обратно пропорциональна эпсилону. Если эпсилон большой, то ошибка должна быть маленькой, и наоборот. Я протестировал значения эпсилона в диапазоне от e^-10 до e^10 (обратите внимание на логарифмический масштаб).

В тесте использовался датасет произвольного неизменного размера в 10 600 строк.

Среднеквадратичная ошибка



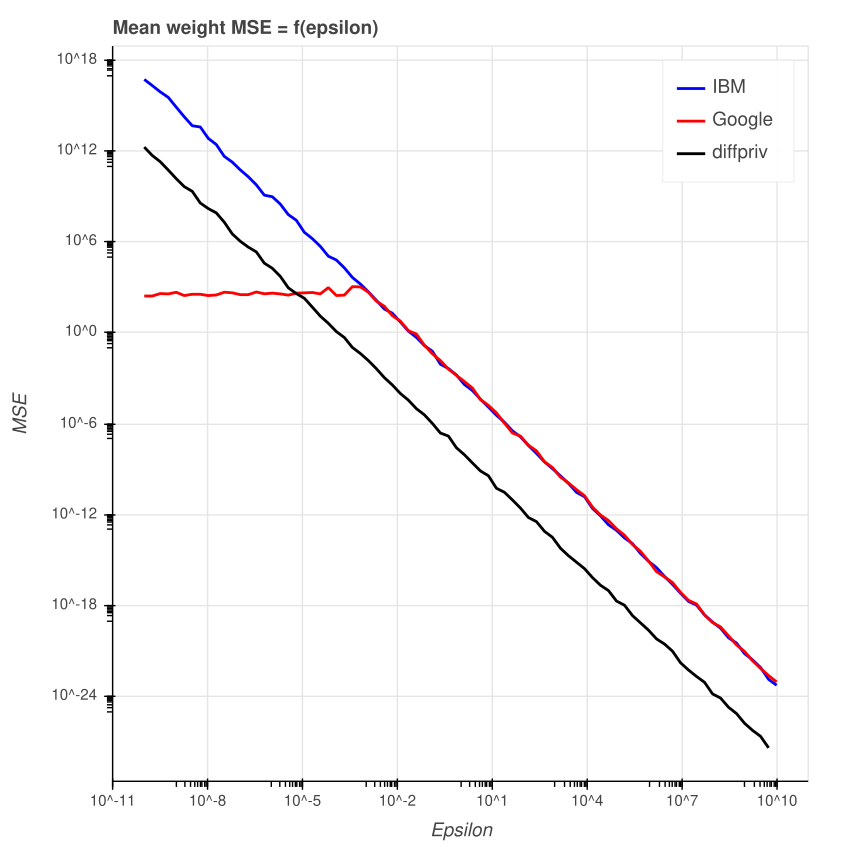
Действительно, ошибка уменьшается по мере увеличения эпсилона. Интересно, что библиотека Google имеет ограничение по среднеквадратичной ошибке, если значение эпсилона очень мало. В библиотеках IBM и diffpriv этого не наблюдается.

Причина этого кроется во фрагменте исходного кода библиотеки Google. В numerical-mechanisms.h:

 // Добавляет шум к значению дифференциальной приватности. 
 // Для этого privacy_budget умножается на эпсилон. Бюджет приватности
  // должен находиться в пределах (0, 1], и это способ разделения эпсилона между несколькими значениями.
  // Например, если пользователь хочет добавить шум к двум разным значениям
  // с помощью заданного эпсилона, то он может добавить шум к каждому значения с бюджетом 0.5 (или 0.4, или 0.6 и т.д.).
  virtual double AddNoise(double result, double privacy_budget) {
    if (privacy_budget <= 0) {
      privacy_budget = std::numeric_limits<double>::min();
    }
    // Реализует snapping-механизм, описанный Мироновым
    // (2012, "On Significance of the Least Significant Bits For Differential Privacy").
    double noise = distro_->Sample(1.0 / privacy_budget);
    double noised_result =
        Clamp<double>(LowerBound<double>(), UpperBound<double>(), result) +
        noise;
    double nearest_power = GetNextPowerOfTwo(diversity_ / privacy_budget);
    double remainder =
        (nearest_power == 0.0) ? 0.0 : fmod(noised_result, nearest_power);
    double rounded_result = noised_result - remainder;
    return ClampDouble<double>(LowerBound<double>(), UpperBound<double>(),
                               rounded_result);
  }

В bounded-mean.h:

   // Нормальная ситуация: у нас есть данные.
    double normalized_sum = sum_mechanism_->AddNoise(
        sum - raw_count_ * midpoint_, remaining_budget);
    double average = normalized_sum / noised_count + midpoint_;
    AddToOutput<double>(&output, Clamp<double>(lower_, upper_, average));
    return output;

Когда эпсилон очень маленький (примерно меньше 0,013), расхождение (равное 1/эпсилон) будет крайне большим, а добавляемый шум — нулевым. Поэтому библиотека возвращает среднее ДП, эквивалентное середине диапазона, используемого для среднего значения. Этого объясняет начало красной линии на графике.

У diffpriv среднеквадратичная ошибка меньше, а значит лучше точность по сравнению с двумя другими библиотеками в случае использование одного и того же эпсилона. Чтобы обеспечить с помощью diffpriv тот же уровень приватности, что и у «конкурентов», нужно применять более низкое значение эпсилона.

Стандартное отклонение


Стандартное отклонение ошибки при 100 прогонах выглядит так:


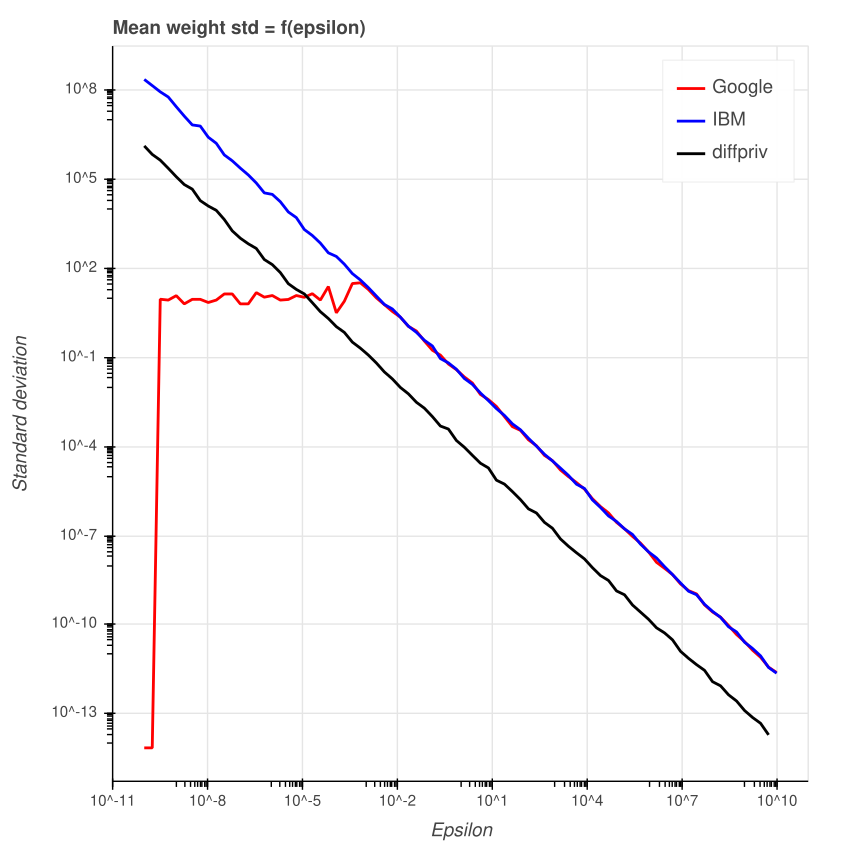
У библиотеки Google при маленьком значении эпсилон отклонение примерно постоянное, а затем быстро догоняет библиотеку IBM. В целом, у diffpriv стандартное отклонение меньше, чем у остальных.

Как размер датасета влияет на точность


Речь идёт о влиянии на точность среднего значения ДП.

Один из рисков маленького датасета заключается в том, что отдельные люди оказывают большое влияние на агрегированное значение, которым является среднее. Таким образом, если в датасете лишь один человек, то идеально точное среднее значение будет равно точному весу этого человека. Давайте посмотрим, как библиотеки помогают избегать раскрытия индивидуальной информации при изменениях размеров датасетов.

Будем использовать произвольное постоянное значение эпсилон 1.0.

Среднеквадратичная ошибка



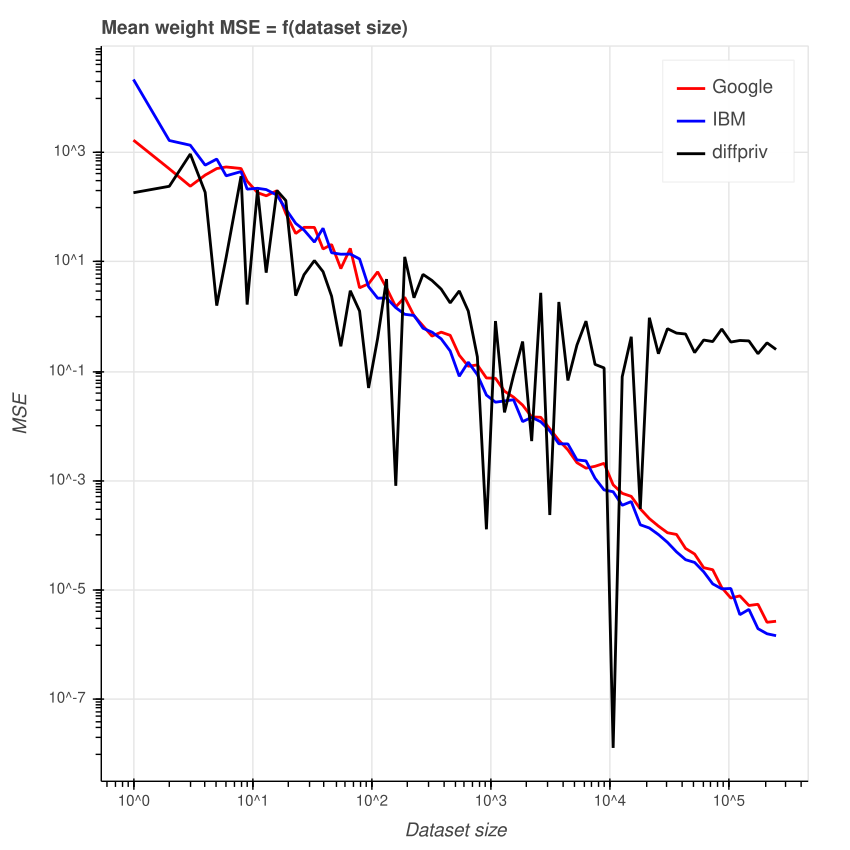
При уменьшении размера датасета среднеквадратичная ошибка растёт, и наоборот. Это было ожидаемо. Если людей мало, то хочется добавить больше шума, чтобы избежать раскрытия приватных данных. Недостатком является то, что для маленьких датасетов агрегированные значения могут стать совершенно нерелевантными из-за очень низкой точности.

Что касается diffpriv, то среднеквадратичная ошибка гораздо сильнее зависит от изменений размера датасета. Впрочем, паттерн всё ещё заметен, как и в двух других библиотеках: с ростом датасета среднеквадратичная ошибка уменьшается. Но это справедливо только для датасетов примерно до 30 000 строк. Потом ошибка мало меняется. Также обратите внимание на аномальное падение размера ошибки при размере датасета 17 912.

Стандартное отклонение


Вы могли спросить, как размер добавляемого шума менялся в течение 100 прогонов для заданного размера датасета? Чтобы ответить на это, давайте построим график стандартного отклонения ошибки для 100 прогонов для каждого размера датасата.


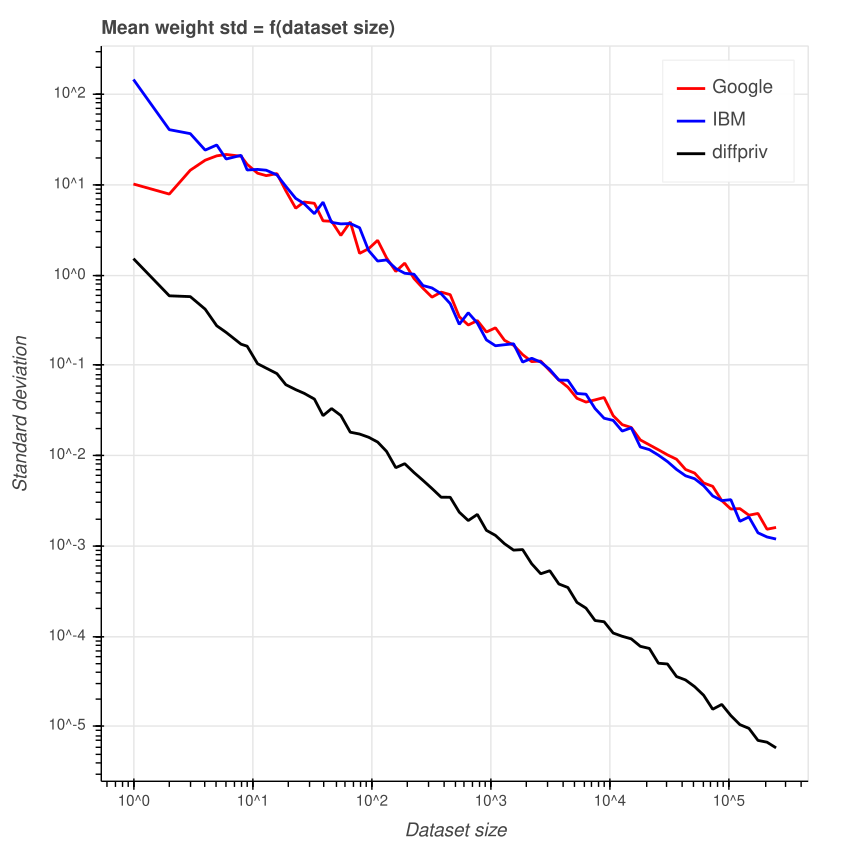
При маленьких датасетах колебание ошибки выше. Однако у библиотеки Google возникает пик при датасете размером 6. У более маленьких и более крупных датасетов колебания меньше. У библиотеки IBM этого не наблюдается, график ближе к линейному.

Повторюсь, у diffpriv в целом стандартное отклонение ниже.

Заключение


Мы увидели, что меры, принятые в трёх разных библиотеках дифференциальной приватности, соответствуют исходным ожиданиям. Однако разная реализация приводит к разным результатам, особенно в граничных случаях, как в случае с очень маленькими значениями эпсилона и библиотекой Google. На практике это не должно мешать, потому что пользователи не будут применять очень большие и очень маленькие датасеты, как и очень маленькие значения эпсилона. Впрочем, в подобных ситуациях библиотека может выдать предупреждение.

Поведение diffpriv заметно отличается от двух других библиотек, так что мы рекомендуем внимательно подходить к выбору значения эпсилона.

Ссылки