После всех вычислений, приведенных в этой и этой публикациях, можно углубиться в статистический анализ и рассмотреть метод наименьших квадратов. Для этой цели используется библиотека statsmodels, которая позволяет пользователям исследовать данные, оценивать статистические модели и выполнять статистические тесты. За основу были взяты эта статья и эта статья. Само описание используемой функции на английском доступно по следующей ссылке.
Сначала немного теории:
Линейная регрессия используется в качестве прогнозирующей модели, когда предполагается линейная зависимость между зависимой переменной (переменная, которую мы пытаемся предсказать) и независимой переменной (переменная и/или переменные, используемые для предсказания).
В самом простой случае при рассмотрении используется одна переменная на основании которой мы пытаемся предсказать другую. Формула в этом случае имеет следующий вид:
Y = C + M*X
В действительности так же может существовать связь между зависимой переменной и несколькими независимыми переменными. Для этих типов моделей (при условии линейности) мы можем использовать множественную линейную регрессию следующего вида:
Y = C + M1X1 + M2X2 + …
Про данный коэффициент написано уже много, для примера на этой странице
Коротко, если не вдаваться в подробности, то можно его охарактеризовать следующим образом:
Акции c бета-коэффициентом:
Другими словами, если акция увеличится на 14%, в то время как рынок вырос всего на 10%, то бета-коэффициент акции составит 1,4. Как правило на рынках с более высоким бета-коэффициентом можно предположить лучшие условия для вознаграждения (а следовательно и для риска).

Следующий код Python включает в себя пример линейной регрессии, где входной переменной является доходность по Индексу МосБиржи, а оцениваемая переменная — доходность по акциям Аэрофлот.
Для того, чтобы отсутствовала необходимость вспоминать как загружать данные и приводить данные к форме, необходимой для расчета — код приводиться с момента загрузки данных и до получения результатов. Вот полный синтаксис для выполнения линейной регрессии в Python с использованием statsmodels:
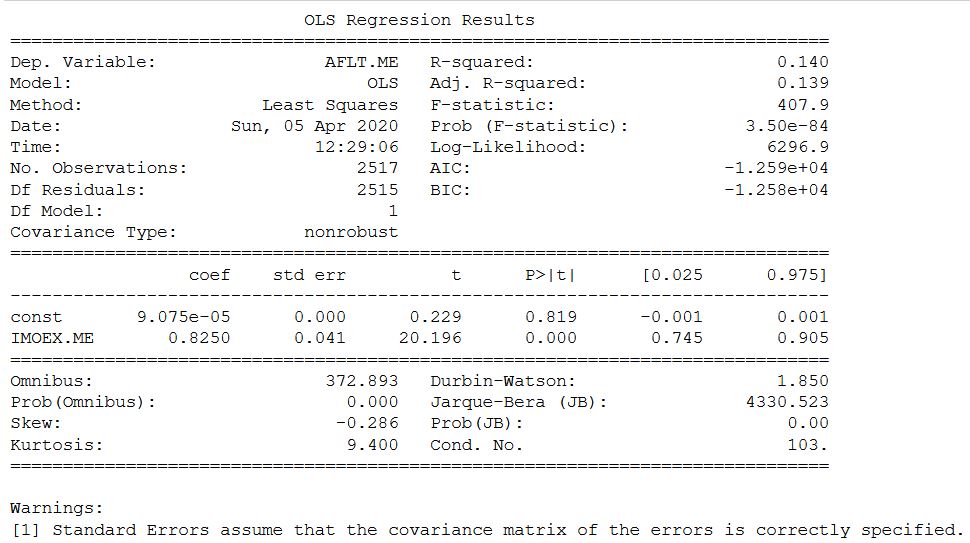
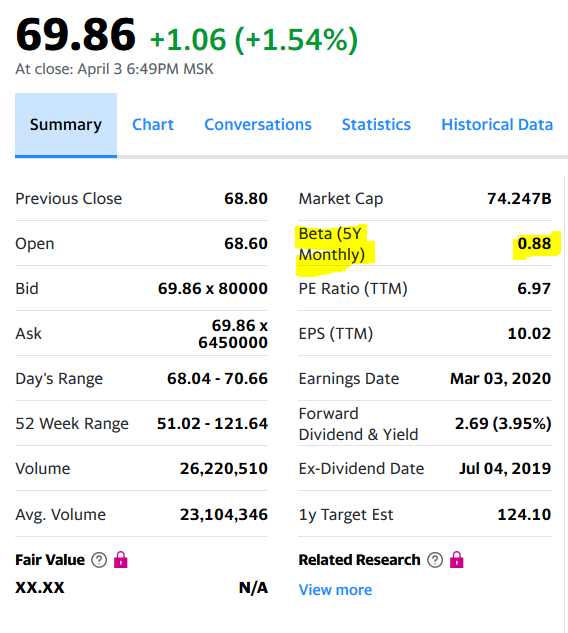
На сайте yahoo и Мосбиржи бета коэффициент отличается незначительно в большую сторону. Но надо честно признаться, что расчет для некоторых других акций с российской биржи показал более значительные отличия, но в пределах интервала.
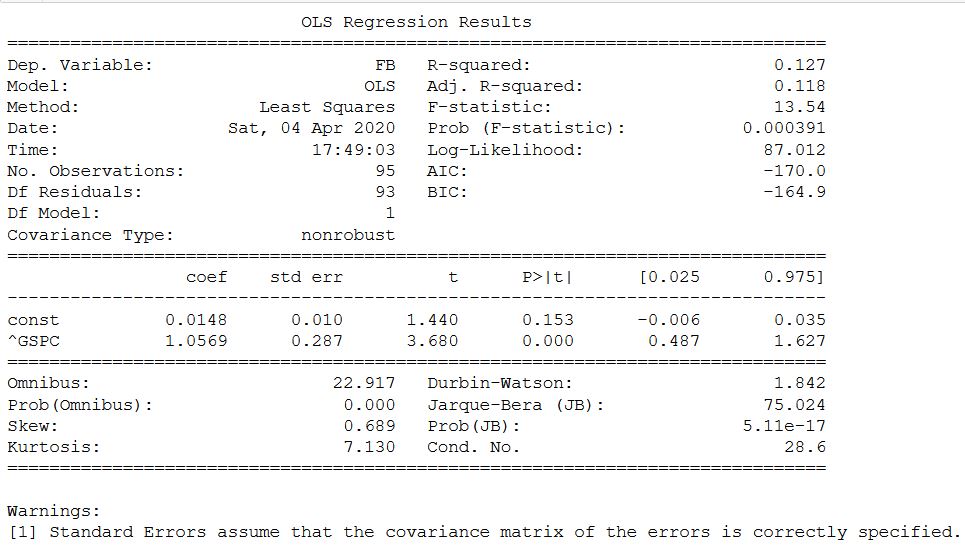
Тот же анализ для акции FB и индекса SP500. Здесь вычисление, как в оригинале, проводится через месячную доходность.
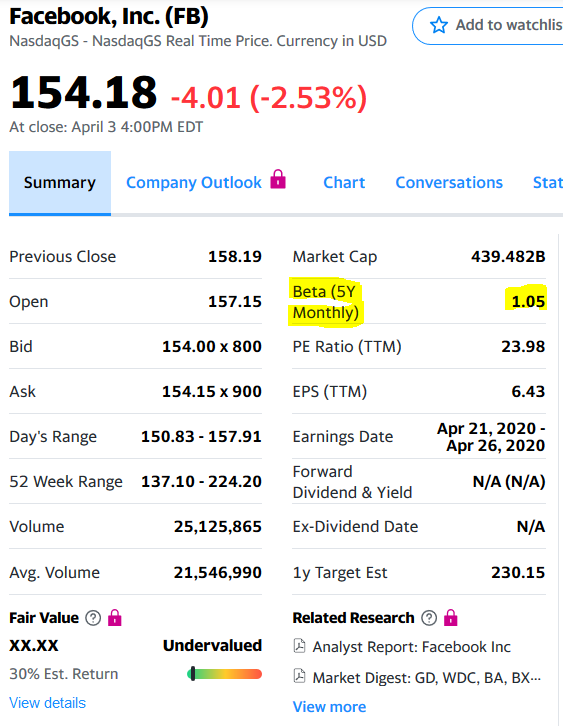
В этом случае все совпало и подтвердило возможность использование statsmodels для определения коэффициента бета.
Ну и в качестве бонуса — если Вы хотите получить только бета — коэффициент и остальную статистику вы хотите оставить в стороне, то предлагается еще один код для его расчета:
Правда это не означает, что всю остальные получаемые значения надо игнорировать, но для их понимания понадобятся знание статистики. Приведу небольшую выдержку из получаемых значений:
На этом пока что все. Конечно, представляет интерес поискать зависимость между различными величинами для того, чтобы через одну предсказать другую и получить профит. В одном из иностранных источников встретилось предсказание индекса через процентную ставку и уровень безработицы. Но если изменение процентной ставки в России можно взять с сайта Центробанка, то другие пока продолжаю искать. К сожалению, на сайте Росстата не удалось найти актуальные. Это заключительная публикация в рамках статей общего финансового анализа.
Сначала немного теории:
О линейной регрессии
Линейная регрессия используется в качестве прогнозирующей модели, когда предполагается линейная зависимость между зависимой переменной (переменная, которую мы пытаемся предсказать) и независимой переменной (переменная и/или переменные, используемые для предсказания).
В самом простой случае при рассмотрении используется одна переменная на основании которой мы пытаемся предсказать другую. Формула в этом случае имеет следующий вид:
Y = C + M*X
- Y = зависимая переменная (результат / прогноз / оценка)
- C = Константа (Y-Intercept)
- M = Наклон линии регрессии (угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем X на одну единицу)
- X = независимая переменная (предиктор, используемый в прогнозе Y)
В действительности так же может существовать связь между зависимой переменной и несколькими независимыми переменными. Для этих типов моделей (при условии линейности) мы можем использовать множественную линейную регрессию следующего вида:
Y = C + M1X1 + M2X2 + …
Бета — коэффициент
Про данный коэффициент написано уже много, для примера на этой странице
Коротко, если не вдаваться в подробности, то можно его охарактеризовать следующим образом:
Акции c бета-коэффициентом:
- ноль указывает на отсутствие корреляции между акцией и индексом
- единица указывает на то, что акция имеет ту же волатильность, что и индекс
- больше одного — указывает на большую доходность (а следовательно и риски) акции, чем индекс
- менее единицы — менее волатильная акция, чем индекса
Другими словами, если акция увеличится на 14%, в то время как рынок вырос всего на 10%, то бета-коэффициент акции составит 1,4. Как правило на рынках с более высоким бета-коэффициентом можно предположить лучшие условия для вознаграждения (а следовательно и для риска).

Практика
Следующий код Python включает в себя пример линейной регрессии, где входной переменной является доходность по Индексу МосБиржи, а оцениваемая переменная — доходность по акциям Аэрофлот.
Для того, чтобы отсутствовала необходимость вспоминать как загружать данные и приводить данные к форме, необходимой для расчета — код приводиться с момента загрузки данных и до получения результатов. Вот полный синтаксис для выполнения линейной регрессии в Python с использованием statsmodels:
#Загружаем библиотеки
import pandas as pd
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
#Загружаю данные
ticker = ['AFLT.ME','IMOEX.ME']
stock = yf.download(ticker)
# Выделение скорректированой цены закрытия
all_adj_close = stock[['Adj Close']]
# Вычисление доходности
all_returns = np.log(all_adj_close / all_adj_close.shift(1))
# Выделение доходности по акциям
aflt_returns = all_returns['Adj Close'][['AFLT.ME']].fillna(0)
# Выделение доходности по индексу МосБиржи
moex_returns = all_returns['Adj Close'][['IMOEX.ME']].fillna(0)
# Создание нового DataFrame
return_data = pd.concat([aflt_returns, moex_returns], axis=1)[1:]
return_data.columns = ['AFLT.ME', 'IMOEX.ME']
# Добавляем столбец единиц и определяем X и y
X = sm.add_constant(return_data['IMOEX.ME'])
y = return_data['AFLT.ME']
# Создание модели
model_moex = sm.OLS(y,X).fit()
# Вывод результатов
print(model_moex.summary())

На сайте yahoo и Мосбиржи бета коэффициент отличается незначительно в большую сторону. Но надо честно признаться, что расчет для некоторых других акций с российской биржи показал более значительные отличия, но в пределах интервала.

Тот же анализ для акции FB и индекса SP500. Здесь вычисление, как в оригинале, проводится через месячную доходность.
sp_500 = yf.download('^GSPC')
fb = yf.download('FB')
# Пересчет в месячную доходность
fb = fb.resample('BM').apply(lambda x: x[-1])
sp_500 = sp_500.resample('BM').apply(lambda x: x[-1])
monthly_prices = pd.concat([fb['Close'], sp_500['Close']], axis=1)
monthly_prices.columns = ['FB', '^GSPC']
monthly_returns = monthly_prices.pct_change(1)
clean_monthly_returns = monthly_returns.dropna(axis=0)
X = clean_monthly_returns['^GSPC']
y = clean_monthly_returns['FB']
X1 = sm.add_constant(X)
model_fb_sp_500 = sm.OLS(y, X1)
results_fb_sp_500 = model_fb_sp_500.fit()
print(results_fb_sp_500.summary())


В этом случае все совпало и подтвердило возможность использование statsmodels для определения коэффициента бета.
Ну и в качестве бонуса — если Вы хотите получить только бета — коэффициент и остальную статистику вы хотите оставить в стороне, то предлагается еще один код для его расчета:
from scipy import stats
slope, intercept, r_value, p_value, std_err = stats.linregress(X, y)
print(slope)
1.0568997978702754
Правда это не означает, что всю остальные получаемые значения надо игнорировать, но для их понимания понадобятся знание статистики. Приведу небольшую выдержку из получаемых значений:
- R-squared, который является коэффициентом детерминации и принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость;
- Adj. R-squared — скорректированный R-squared на основании числа наблюдений и числа степеней свободы;
- std err — стандартная ошибка оценки коэффициента;
- P>|t| — р-значение Величина менее 0,05 считается статистически значимой;
- 0.025 и 0.975 — нижнее и верхнее значения доверительного интервала.
- и т.д.
На этом пока что все. Конечно, представляет интерес поискать зависимость между различными величинами для того, чтобы через одну предсказать другую и получить профит. В одном из иностранных источников встретилось предсказание индекса через процентную ставку и уровень безработицы. Но если изменение процентной ставки в России можно взять с сайта Центробанка, то другие пока продолжаю искать. К сожалению, на сайте Росстата не удалось найти актуальные. Это заключительная публикация в рамках статей общего финансового анализа.


empenoso
А как берете данные с Yahoo! Finance?