Сейчас занимаюсь разработкой калькулятора для печатных плат и изучаю расчетные модели, которые стоят за табличными формулами. Добрался до волнового сопротивления микрополосковой линии и решил рассказать про модель Гарольда Уилера и то, как его Эрик Богатин недооценил, а оказалось, что у меня тут публикаций на тему волнового сопротивления вообще не было, поэтому сначала немного теории, а потом к восстановлению справедливости.
Волновое сопротивление для линии без потерь выражается всем известной формулой:
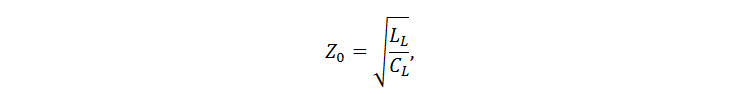
где LL и CL – погонные индуктивность и ёмкость линии (то есть в расчёте на единицу длины). Думаю, будет полезно пояснить, откуда она берётся. Рассмотрим предельно малый участок длинной двухпроводной линии передачи, по которой течёт переменный ток (рис. 1). Ток переменный, поэтому мгновенные значения тока, напряжения между проводами, линейной плотности электрического заряда меняются вдоль проводов.
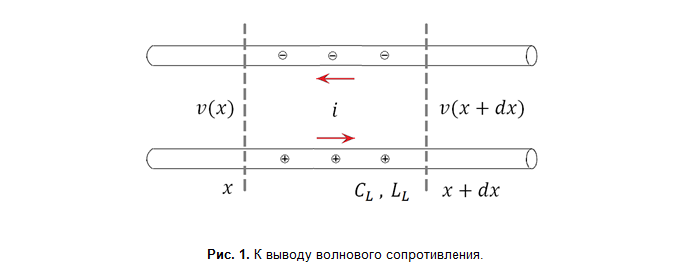
Закон сохранения заряда для участка провода и закон Фарадея для контура выглядят следующим образом:

Для линии без потерь (RL = 0) и с учётом ?L = LL • i и qL = CL • v получим:
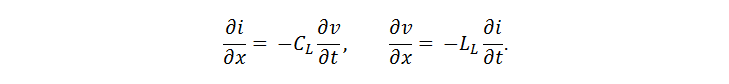
Эти дифференциальные уравнения приводятся к волновой форме, для которой получаем:
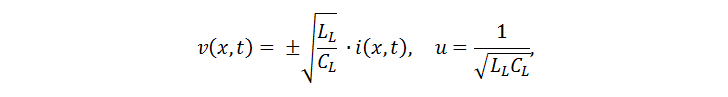
где u – скорость распространения волны, а коэффициент, связывающий ток в проводах и напряжение между проводами – волновое сопротивление. Сразу приведем полезные соотношения (TD – временная задержка линии):
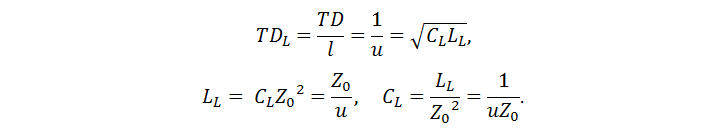
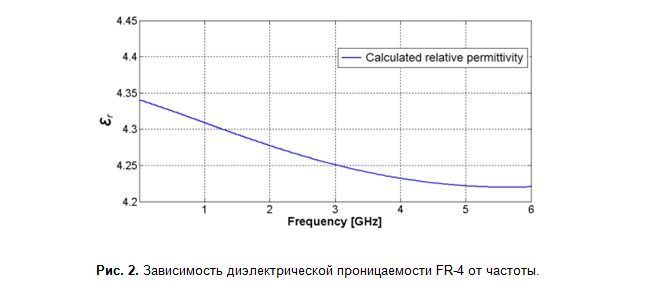
Ёмкость и индуктивность зависят от частоты, поэтому и волновое сопротивление меняется с изменением частоты. Влияние скин-эффекта на индуктивность ограничивается частотами до нескольких десятков мегагерц, в верхнем диапазоне частот она меняется незначительно. На значение ёмкости оказывает зависимость диэлектрической проницаемости материала печатной платы от частоты, а для микрополосковых линий из-за несимметричности диэлектрика ещё и эффект дисперсии. Данные для стеклотекстолита FR-4 в различных источниках отличаются, однако в качестве оценки можно принять, что диэлектрическая проницаемость снижается на 0,15-0,2 каждую декаду (рис. 2). Отличие в данных объясняется тем, что FR-4 — это класс материалов. Он состоит из стекловолокна и эпоксидной смолы, имеющих значительно отличающиеся диэлектрические проницаемости (рис. 3). Чем больше смолы в материале, тем меньше усреднённое по объёму значение диэлектрической проницаемости стеклотекстолита. Отсюда разные значения у разных производителей.

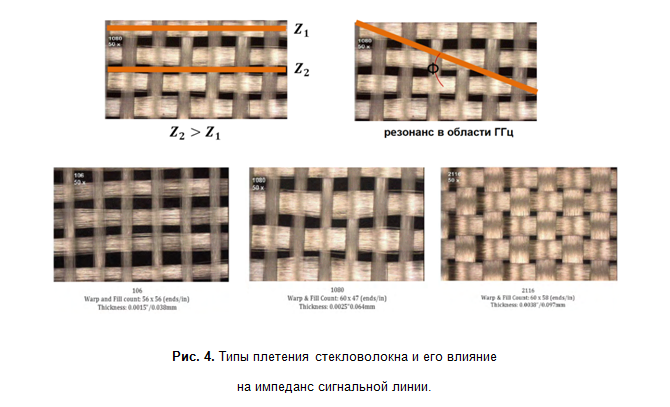
Взаимное расположение волокон стекловолокна и проводника также влияет на волновое сопротивление. Если проводник расположен над волокном, то его волновое сопротивление будет несколько выше по сравнению с соседним проводником, который попал в промежуток между волокнами. Если проводник направлен под углом к волокнам, то это приводит к периодическому изменению волнового сопротивления и резонансным эффектам на частотах в области десяток ГГц. Степень влияния значительно зависит от типа плетения стекловолокна (рис. 4). Именно поэтому существуют специализированные материалы для высокочастотных печатных плат, где влияние этих эффектов становится значимым. Параметры таких диэлектриков обладают лучшей стабильностью в широком диапазоне частот и гораздо лучше документированы.
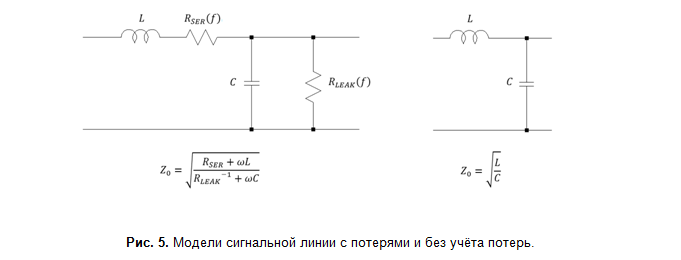
Что касается потерь (рис. 5), то для большинства практических случаев применима модель с низкими потерями (англ. low-loss model), для которой на высоких частотах потерями можно пренебречь RSER? ?L, RLEAK?1??C. Такое упрощение позволило разработать эффективные модели, позволяющие с высокой точностью вычислять параметры сигнальных линий при помощи стандартных функций.
Планарные сигнальные линии были изобретены в начале 50-ых годов прошлого столетия, и для полосковых линий почти сразу были разработаны точные математические модели, а на создание точной модели анализа микрополосковой линии понадобилось несколько десятилетий. Одним из первых (в 1965 году) точные решения для частных случаев дал Гарольд Уилер, которые позже (к 1977 году) были им обобщены. Причина в несимметричности диэлектрика, которая приводит к сложному распределению электрического поля, которое ещё и зависит от частоты.
Естественно, эта модель была не единственная – и к 1988 году их накопилось достаточное количество, чтобы их было интересно сравнить. Это сделал великий и ужасный Эрик Богатин. Я наткнулся на эту статью, когда выбирал расчётную модель для калькулятора. Потом я добрался до публикаций Уилера, где много страниц крутой математики с конформными преобразованиями, и понял, что Богатин невнимательно его читал (или вообще не читал) и загрубил его модель, что повлияло на результаты сравнения. Потом эта ошибка перекочевала в 2007-ой год. При этом сам Богатин ссылается на монографию ”Microwave Transmission Line Impedance Data” некоего М.А.Р. Гунстана, но я уже не стал дальше копать, откуда ноги растут, признав виновником товарища Богатина (которого я, кстати, очень уважаю, Богатин – сила).
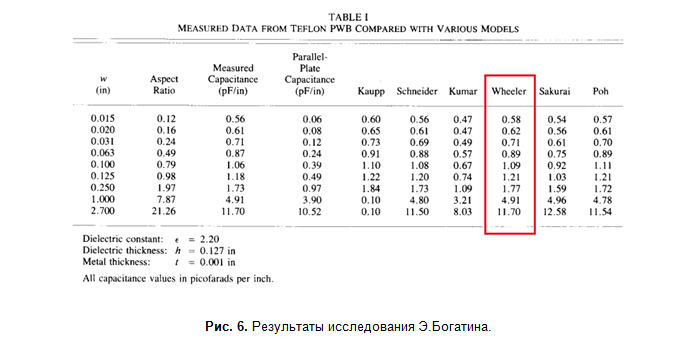
Итак, в чём суть. Богатин экспериментально измерял погонную ёмкость микрополосковых линий различной ширины (на частоте 1 кГц) и сравнивал с расчётными значениями (рис. 6).
Во всех моделях, у которых я изучал первоисточники, приводятся аналитические соотношения для волнового сопротивления. Ёмкость же рассчитывается, используя следующее соотношение:
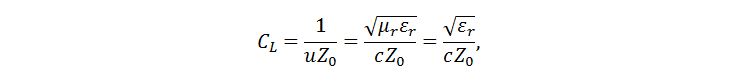
где ?r – диэлектрическая проницаемость, c – скорость света. Несимметричность диэлектрика приводит к тому, что приходится изобретать эффективное значение диэлектрической проницаемости. Богатин пишет:
и использует гибридную модель «Уилера-Шнайдера» (результат в пФ/дюйм):
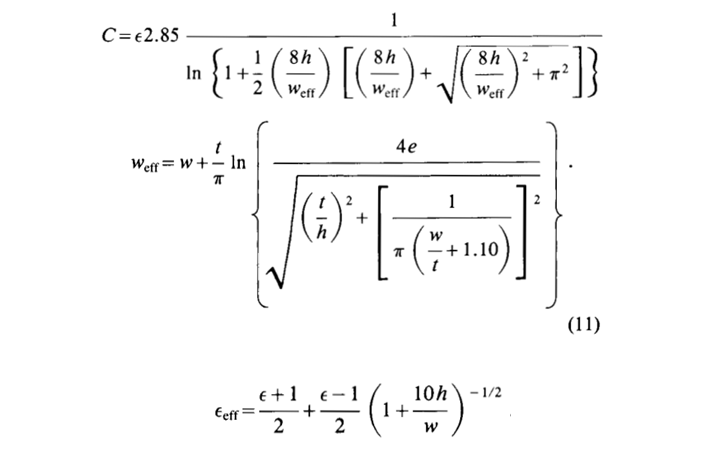
Модель даёт по результатам эксперимента неплохую точность и Богатин хвалит свой изобретённый велосипед:
А теперь обратимся к первоисточнику. Те формулы, которые использует Богатин – это упрощённые формулы для случая без диэлектрика:
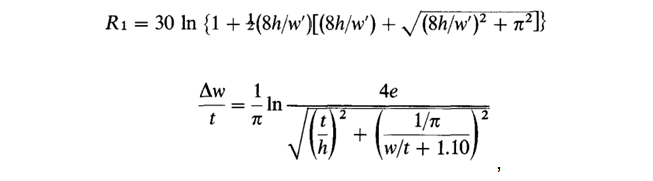
а полная модель выглядит так:
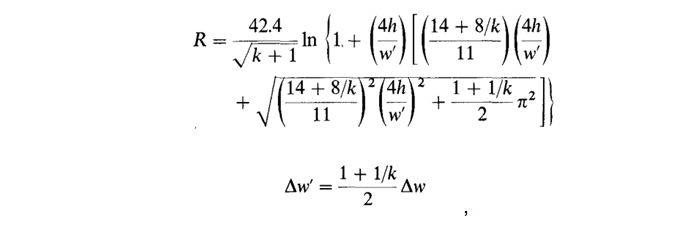
здесь в обозначениях Уилера R – волновое сопротивление, k – диэлектрическая проницаемость, R1 = R(k = 1) – сопротивление без диэлектрика, ?w – корректировка ширины, учитывающая толщину проводника, ?w’ – корректировка с учётом влияния диэлектрика. Для эффективного значения диэлектрической проницаемости Уилер использует обозначение k' и приводит для него следующую формулу:
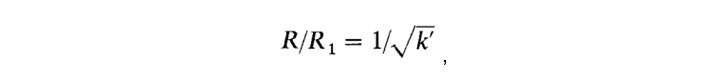
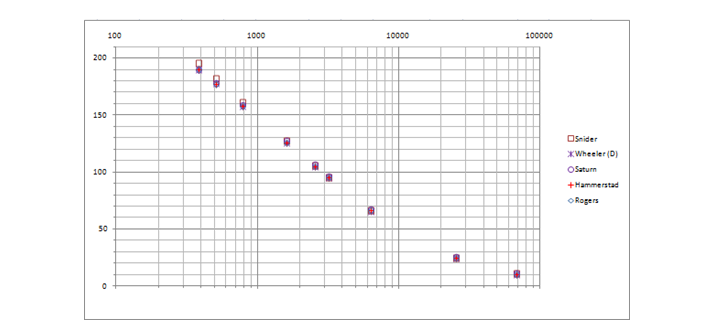
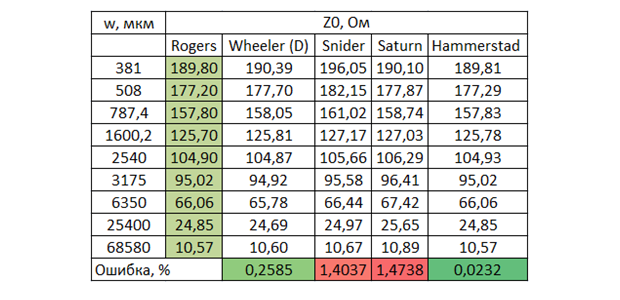
которая не так проста, конечно, как у Шнайдера, но тем не менее, она в модели есть. Я повторил расчёты Богатина, оставив самые точные модели: Шнайдера, Уилера, их гибридный вариант – и добавил результаты расчёта с помощью калькулятора Saturn PCB Toolkit и модели Хаммерстэда. Для наглядности привожу и график, и табличные данные с ошибкой относительно экспериментальных данных.
С учётом погрешностей измерения и значения диэлектрической проницаемости базового материала (2,2 ± 1%) можно сказать, что все модели хорошо коррелируют с экспериментальными данными, не зря исследователи годами формулы подгоняли. От Saturn ожидал большей точности, так как там прямо написано, что он использует «не простую, а сложную» формулу и точность сравнима с Sonnet 3D. К тому же там толщину можно только в унциях выбирать, а это либо ? oz. (18 мкм), либо 1 oz. (35 мкм), а 1 мил (25,4 мкм) не задать. Значения в таблице приведены для ? oz., так как они ближе к экспериментальным данным так получаются. Также очевидно, что исходная модель Уилера дала бы большую точность на этой выборке данных, поэтому мне и было за него досадно. Особенно с учётом того, что как раз-таки модель Шнайдера имеет серьёзный недостаток – она не учитывает влияние толщины проводника, что почти не влияет на ёмкость, но значимо для индуктивности и поэтому самого волнового сопротивления. Богатин значения волнового сопротивления, к сожалению, не приводит, поэтому в качестве опорного значения использовал калькулятор от уважаемой фирмы Rogers. В Saturn в это раз 1 oz. несколько лучшую точность дало, не очень мне пока понятна логика его работы. На графике видно, что при снижении ширины (где влияние толщины возрастает) Шнайдер отваливается. А Rogers, видимо, как раз на модели Хаммерстэда основан. Я первоначально на Уилере сделал, но раз большинство продвинутых калькуляторов на Хаммерстэде, то можно будет на эту модель перейти, чтоб от них не отставать (хотя в модель нет явной формулы для синтеза, в отличие от уилеровской).
Собственно, на этом считаю справедливость восстановленной. Уилер — мощь. Даже Богатин иногда ошибается. Поэтому не доверяйте, проверяйте и перепроверяйте. Используйте расчёты для Ваших сигнальных линий. Кстати. Просьба поделится в комментариях, используете ли Вы расчёт волнового сопротивления и если да, то с помощью чего считаете?
P.S. Я в процессе работы над калькулятором и книгу дорабатываю, сейчас до бесплатной версии руки дошли – добавил все улучшения и исправления, которые были до этого только в полную внесены. Всем удачи!
Волновое сопротивление для линии без потерь выражается всем известной формулой:
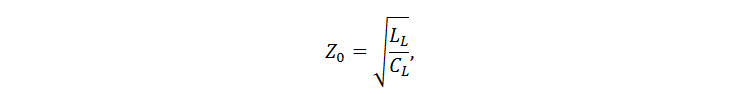
где LL и CL – погонные индуктивность и ёмкость линии (то есть в расчёте на единицу длины). Думаю, будет полезно пояснить, откуда она берётся. Рассмотрим предельно малый участок длинной двухпроводной линии передачи, по которой течёт переменный ток (рис. 1). Ток переменный, поэтому мгновенные значения тока, напряжения между проводами, линейной плотности электрического заряда меняются вдоль проводов.

Закон сохранения заряда для участка провода и закон Фарадея для контура выглядят следующим образом:

Для линии без потерь (RL = 0) и с учётом ?L = LL • i и qL = CL • v получим:
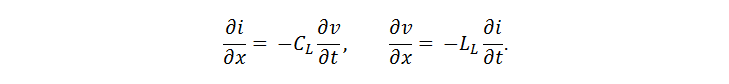
Эти дифференциальные уравнения приводятся к волновой форме, для которой получаем:
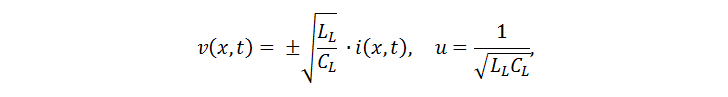
где u – скорость распространения волны, а коэффициент, связывающий ток в проводах и напряжение между проводами – волновое сопротивление. Сразу приведем полезные соотношения (TD – временная задержка линии):
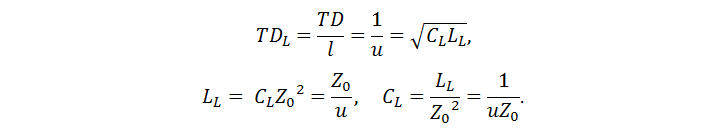
Ёмкость и индуктивность зависят от частоты, поэтому и волновое сопротивление меняется с изменением частоты. Влияние скин-эффекта на индуктивность ограничивается частотами до нескольких десятков мегагерц, в верхнем диапазоне частот она меняется незначительно. На значение ёмкости оказывает зависимость диэлектрической проницаемости материала печатной платы от частоты, а для микрополосковых линий из-за несимметричности диэлектрика ещё и эффект дисперсии. Данные для стеклотекстолита FR-4 в различных источниках отличаются, однако в качестве оценки можно принять, что диэлектрическая проницаемость снижается на 0,15-0,2 каждую декаду (рис. 2). Отличие в данных объясняется тем, что FR-4 — это класс материалов. Он состоит из стекловолокна и эпоксидной смолы, имеющих значительно отличающиеся диэлектрические проницаемости (рис. 3). Чем больше смолы в материале, тем меньше усреднённое по объёму значение диэлектрической проницаемости стеклотекстолита. Отсюда разные значения у разных производителей.


Взаимное расположение волокон стекловолокна и проводника также влияет на волновое сопротивление. Если проводник расположен над волокном, то его волновое сопротивление будет несколько выше по сравнению с соседним проводником, который попал в промежуток между волокнами. Если проводник направлен под углом к волокнам, то это приводит к периодическому изменению волнового сопротивления и резонансным эффектам на частотах в области десяток ГГц. Степень влияния значительно зависит от типа плетения стекловолокна (рис. 4). Именно поэтому существуют специализированные материалы для высокочастотных печатных плат, где влияние этих эффектов становится значимым. Параметры таких диэлектриков обладают лучшей стабильностью в широком диапазоне частот и гораздо лучше документированы.

Что касается потерь (рис. 5), то для большинства практических случаев применима модель с низкими потерями (англ. low-loss model), для которой на высоких частотах потерями можно пренебречь RSER? ?L, RLEAK?1??C. Такое упрощение позволило разработать эффективные модели, позволяющие с высокой точностью вычислять параметры сигнальных линий при помощи стандартных функций.

Планарные сигнальные линии были изобретены в начале 50-ых годов прошлого столетия, и для полосковых линий почти сразу были разработаны точные математические модели, а на создание точной модели анализа микрополосковой линии понадобилось несколько десятилетий. Одним из первых (в 1965 году) точные решения для частных случаев дал Гарольд Уилер, которые позже (к 1977 году) были им обобщены. Причина в несимметричности диэлектрика, которая приводит к сложному распределению электрического поля, которое ещё и зависит от частоты.
Естественно, эта модель была не единственная – и к 1988 году их накопилось достаточное количество, чтобы их было интересно сравнить. Это сделал великий и ужасный Эрик Богатин. Я наткнулся на эту статью, когда выбирал расчётную модель для калькулятора. Потом я добрался до публикаций Уилера, где много страниц крутой математики с конформными преобразованиями, и понял, что Богатин невнимательно его читал (или вообще не читал) и загрубил его модель, что повлияло на результаты сравнения. Потом эта ошибка перекочевала в 2007-ой год. При этом сам Богатин ссылается на монографию ”Microwave Transmission Line Impedance Data” некоего М.А.Р. Гунстана, но я уже не стал дальше копать, откуда ноги растут, признав виновником товарища Богатина (которого я, кстати, очень уважаю, Богатин – сила).
Итак, в чём суть. Богатин экспериментально измерял погонную ёмкость микрополосковых линий различной ширины (на частоте 1 кГц) и сравнивал с расчётными значениями (рис. 6).

Во всех моделях, у которых я изучал первоисточники, приводятся аналитические соотношения для волнового сопротивления. Ёмкость же рассчитывается, используя следующее соотношение:
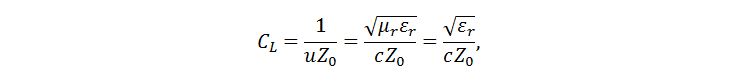
где ?r – диэлектрическая проницаемость, c – скорость света. Несимметричность диэлектрика приводит к тому, что приходится изобретать эффективное значение диэлектрической проницаемости. Богатин пишет:
In the case of Wheeler [13], no model for the effective dielectric constant is offered. However, based on the suggestion by Gunsten [6], the plot for Wheeler’s model uses the effective dielectric constant from Schneider’s model.
и использует гибридную модель «Уилера-Шнайдера» (результат в пФ/дюйм):

Модель даёт по результатам эксперимента неплохую точность и Богатин хвалит свой изобретённый велосипед:
The combination of Wheeler’s and Schneider’s model is found to agree with previous published data and new data presented here to better than 3 percent, and is of a form suitable for use in a spread sheet. In addition to being useful for computer simulation of specific designs, this model can yield some useful insight to add to the intuition of fabrication and design engineers
А теперь обратимся к первоисточнику. Те формулы, которые использует Богатин – это упрощённые формулы для случая без диэлектрика:
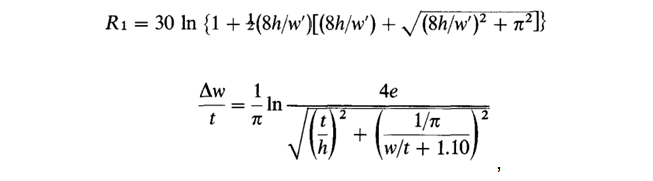
а полная модель выглядит так:
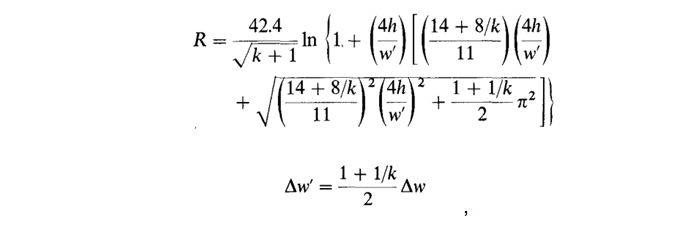
здесь в обозначениях Уилера R – волновое сопротивление, k – диэлектрическая проницаемость, R1 = R(k = 1) – сопротивление без диэлектрика, ?w – корректировка ширины, учитывающая толщину проводника, ?w’ – корректировка с учётом влияния диэлектрика. Для эффективного значения диэлектрической проницаемости Уилер использует обозначение k' и приводит для него следующую формулу:
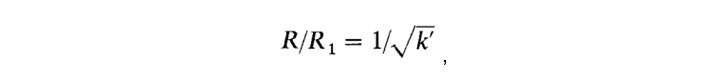
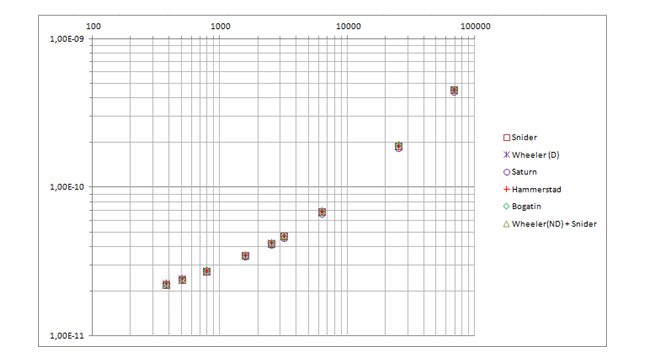
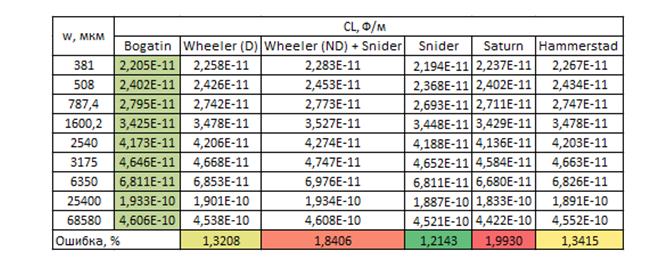
которая не так проста, конечно, как у Шнайдера, но тем не менее, она в модели есть. Я повторил расчёты Богатина, оставив самые точные модели: Шнайдера, Уилера, их гибридный вариант – и добавил результаты расчёта с помощью калькулятора Saturn PCB Toolkit и модели Хаммерстэда. Для наглядности привожу и график, и табличные данные с ошибкой относительно экспериментальных данных.


С учётом погрешностей измерения и значения диэлектрической проницаемости базового материала (2,2 ± 1%) можно сказать, что все модели хорошо коррелируют с экспериментальными данными, не зря исследователи годами формулы подгоняли. От Saturn ожидал большей точности, так как там прямо написано, что он использует «не простую, а сложную» формулу и точность сравнима с Sonnet 3D. К тому же там толщину можно только в унциях выбирать, а это либо ? oz. (18 мкм), либо 1 oz. (35 мкм), а 1 мил (25,4 мкм) не задать. Значения в таблице приведены для ? oz., так как они ближе к экспериментальным данным так получаются. Также очевидно, что исходная модель Уилера дала бы большую точность на этой выборке данных, поэтому мне и было за него досадно. Особенно с учётом того, что как раз-таки модель Шнайдера имеет серьёзный недостаток – она не учитывает влияние толщины проводника, что почти не влияет на ёмкость, но значимо для индуктивности и поэтому самого волнового сопротивления. Богатин значения волнового сопротивления, к сожалению, не приводит, поэтому в качестве опорного значения использовал калькулятор от уважаемой фирмы Rogers. В Saturn в это раз 1 oz. несколько лучшую точность дало, не очень мне пока понятна логика его работы. На графике видно, что при снижении ширины (где влияние толщины возрастает) Шнайдер отваливается. А Rogers, видимо, как раз на модели Хаммерстэда основан. Я первоначально на Уилере сделал, но раз большинство продвинутых калькуляторов на Хаммерстэде, то можно будет на эту модель перейти, чтоб от них не отставать (хотя в модель нет явной формулы для синтеза, в отличие от уилеровской).


Собственно, на этом считаю справедливость восстановленной. Уилер — мощь. Даже Богатин иногда ошибается. Поэтому не доверяйте, проверяйте и перепроверяйте. Используйте расчёты для Ваших сигнальных линий. Кстати. Просьба поделится в комментариях, используете ли Вы расчёт волнового сопротивления и если да, то с помощью чего считаете?
P.S. Я в процессе работы над калькулятором и книгу дорабатываю, сейчас до бесплатной версии руки дошли – добавил все улучшения и исправления, которые были до этого только в полную внесены. Всем удачи!


ne555
«91%» Вас не поняли;)
Вы начали с теории о волновом сопротивлении в идеальной линии.
Вот Вам вопрос в реальной линии (с потерями) и идеальной линии прямого проводника. Какой колебательный контур возникнет при подаче переменного сигнала/тока?
Последовательный, параллельный КК или его отсутствие?
iamsam Автор
Хабр вообще программистский ресурс больше. Определённо точно, у нас очень сильные программисты, но я уверен, что есть и сильные разработчики ПП. Собственно, пишу, чтобы сообщество развивалось, сам тоже хочу учиться. И чтобы 91% понимало :).
Вот Вы задали хороший, я сразу ответ не знал, я в теории цепей не большой специалист. Но попробую дать ответ — зависит от частоты, длины линии и от нагрузки. Может снаружи казаться как параллельная цепь, а может как последовательная. Верно?
ne555
А тут так просто (без математической выкладки) не разобраться.
Просто, Вы в статье активно формулы стали применять для разъяснения вещей, вопрос мой тоже "требует" формул.
DenisHW
Если говорить о первом резонансе, разомкнутая на конце четверть-волновая линия ведет себя как последовательный КК. Закороченная линия, как параллельный КК.
KbRadar
Ответ на этот вопрос зависит от того как соотносится длина линии и частота подаваемого сигнала, что находится в конце линии, как соотносится выходное сопротивление генератора сигнала и волновое сопротивление линии.