
В нескольких предыдущих заметках данной серии мы уже упоминали понятие дифференциального рендеринга. Сегодня пришло время разъяснить что это такое и с чем это едят.
Мы поговорим о том, почему традиционный пайплайн рендеринга не дифференцируем, зачем исследователям в области 3D ML потребовалось сделать его дифференцируемым и как это связано с нейронным рендерингом. Какие существуют подходы к конструированию таких систем, и рассмотрим конкретный пример — SoftRasterizer и его реализацию в PyTorch 3D. В конце, с помощью этой технологии, восстановим все пространственные характеристики “Моны Лизы” Леонардо Да Винчи так, если бы картина была не написана рукой мастера, а отрендерена с помощью компьютерной графики.
Серия 3D ML на Хабре:
- Формы представления 3D данных
- Функции потерь в 3D ML
- Датасеты и фреймворки в 3D ML
- Дифференциальный рендеринг
Репозиторий на GitHub для данной серии заметок.
Заметка от партнера IT-центра МАИ и организатора магистерской программы “VR/AR & AI” — компании PHYGITALISM.
Rendering pipeline: forward and inverse
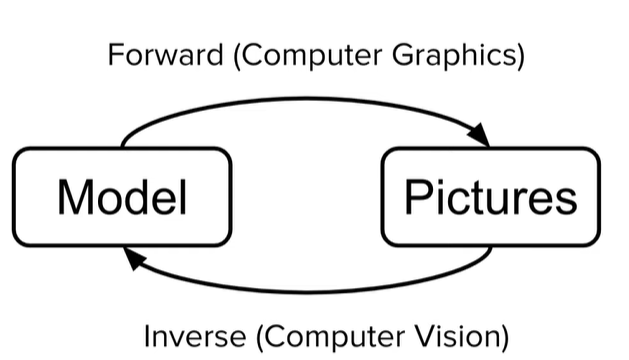
Если мы рассматриваем все возможные задачи, в которых требуется как-то взаимодействовать с 3D моделями, то глобально появляется возможность разделить их на два класса задач:
- Задачи, в которых из 3D сцены мы хотим сгенерировать изображение (такие задачи можно отнести к традиционным задачам компьютерной графике) т.н. forward rendering;
- Задачи, где по изображению нам требуется восстанавливать параметры 3D объектов (такие задачи относятся скорее к компьютерному зрению) т.н. inverse rendering.
До недавнего времени два этих класса задач обычно рассматривались отдельно друг от друга, но сегодня все чаще приходится иметь дело с алгоритмами, которые должны работать в обе стороны (особенно это касается области машинного обучения).
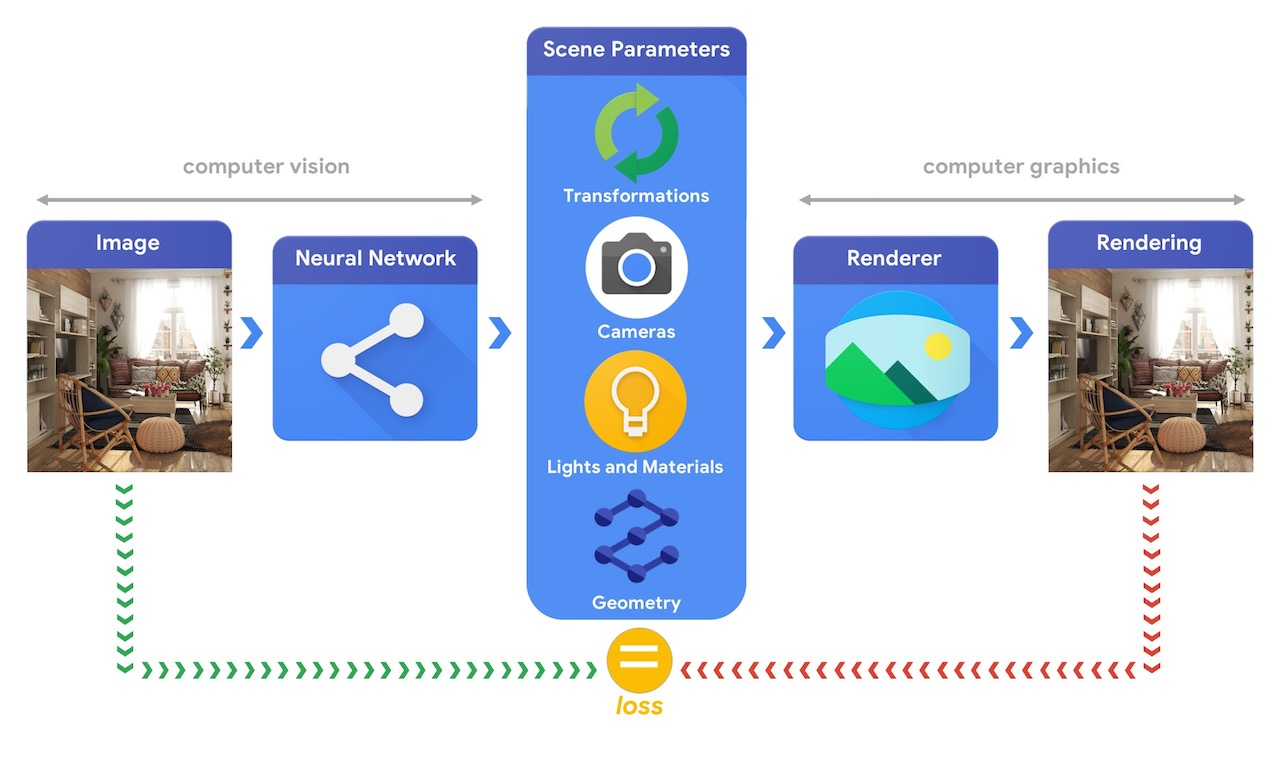
Рис.1 Из презентации TensorFlow Graphics (github page).
В качестве примера такой задачи, можно рассмотреть задачу “3D mesh reconstruction from single image”, которую мы уже упоминали в предыдущих заметках. С одной стороны, эту задачу можно решать сравнивая ошибку рассогласования между исходной моделью и предсказанной с помощью функций потерь для 3D объектов (заметка №2 данной серии). С другой стороны, можно генерировать 3D объект сначала, а после его отрендеренную картинку сравнивать с изображением-образцом (пример на рис.2).
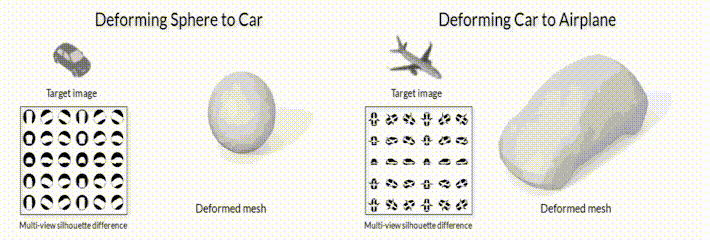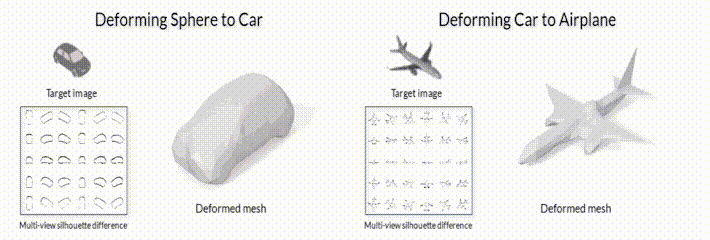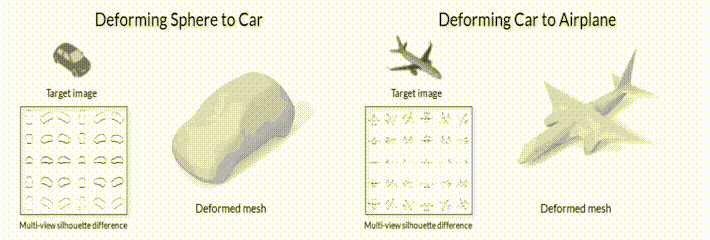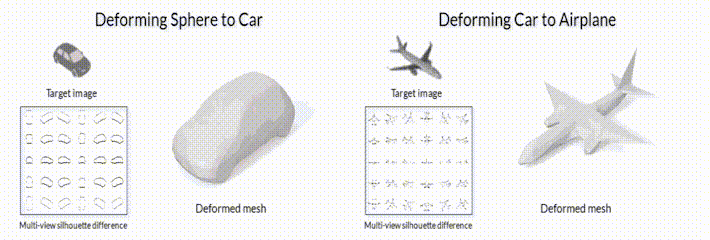
Рис.2 Модель деформации меша с помощью модуля дифференциального рендеринга SoftRas (github page).
Далее, при разговоре про рендеринг, мы будем рассматривать несколько основных компонентов 3D сцены:
- 3D объект, описываемый своим мешем;
- камера с набором характеристик (позиция, направление, раствор и т.д.);
- источники света и их характеристики;
- глобальные характеристики расположения объекта на сцене, описываемые матрицами преобразований.
Процедура прямого рендеринга заключается в функциональном сочетании этих основных компонент, а процедура обратного рендеринга заключается в восстановлении этих компонент по готовому изображению.
Давайте поговорим сначала о том, из каких этапов состоит традиционный пайплайн прямого рендеринга и почему он не является дифференцируемым.
Why is rendering not differentiable?
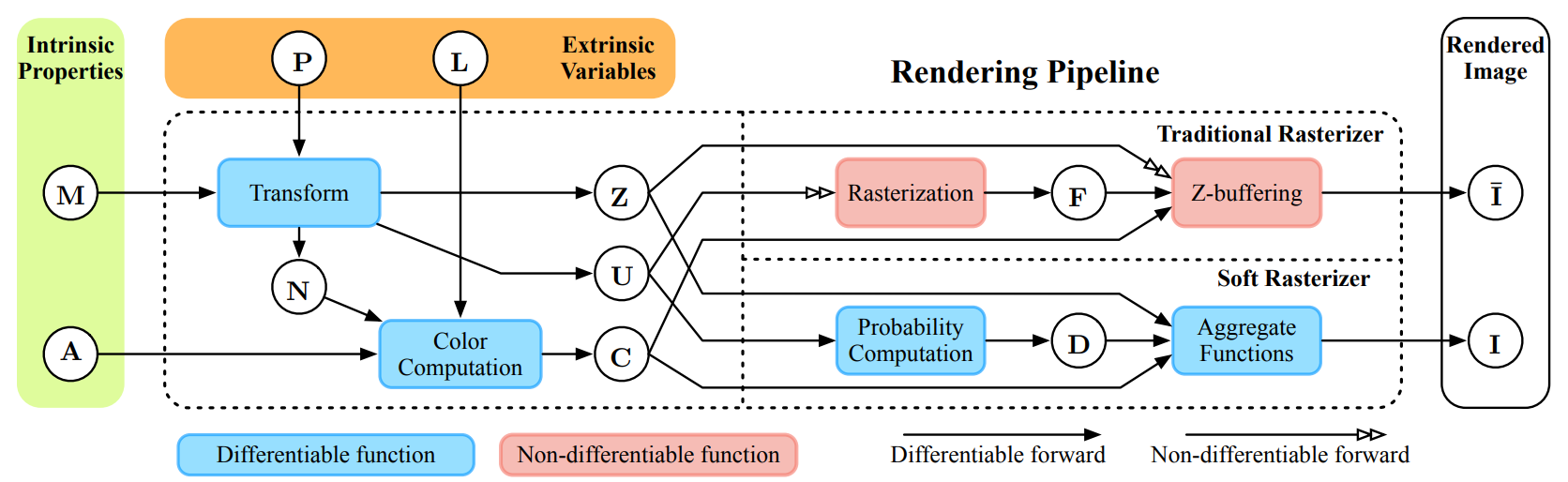
Рис.3 Схема традиционного рендеринга и рендеринга методом Soft Rasterizer [1]. Здесь: — меш объекта на сцене, — модель камеры, — модель источника освещения, — модель текстуры, — карта нормалей для меша, — карта глубины получаемого изображения, — матрица преобразования 3D в 2D для получения плоского изображения, — растеризованное изображение, — вероятностные карты метода Soft Rasterizer, — изображения полученные традиционным рендерингом и методом SoftRas соответственно. Красные блоки — недифференцируемые операции, синии — дифференцируемые.
Процедуру рендеринга можно подразделить на несколько взаимозависимых этапов (этапы традиционного рендеринга приведены на рис.3 — врехняя линия в правой части). Какие-то этапы, к примеру вычисления освещения и позиции камеры, являются дифференцируемыми, поскольку в них участвуют непрерывные функциональные зависимости (см. модель Фонга, на Хабре о ней и моделях освещения писали здесь и здесь), но два последних этапа не являются дифференцируемыми. Давайте разберемся почему.

Последние два этапа, которые являются по сути и ключевыми — это растеризация и шейдинг. (Про реализацию этих этапов на JavaScript на Хабре писали здесь).
Грубо говоря, проблему недифференцируемости растеризации можно описать так: “пиксели — дискретные структуры, с постоянным цветом, а исходная модель непрерывна, поэтому при проецировании из 3D в 2D часть информации теряется”.
Проиллюстрируем две основные проблемы с дифференцируемостью при вычислении цвета и расстояния.
Проблема №1 (недифференцируемость цвета по глубине)
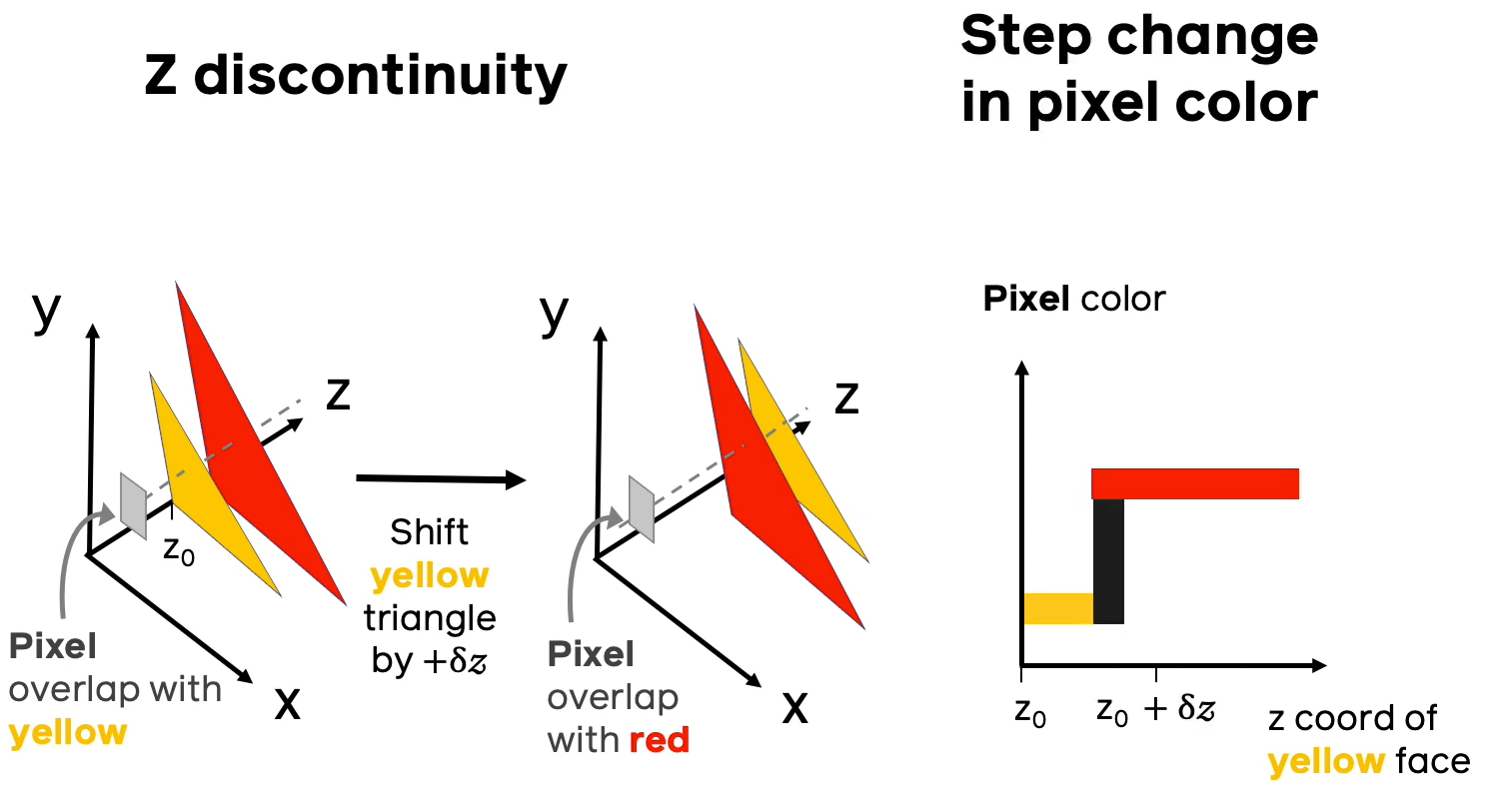
Предположим, что вдоль направления луча, проходящего через пиксель, есть несколько полигонов разных цветов, как на иллюстрации выше. Если придать малый сдвиг полигонов друг относительно друга, может случиться ситуация, когда ближайшим полигоном становится полигон другого цвета и при этом резко меняется цвет, в который нужно разукрашивать соответствующий пиксель. На правом графике иллюстрации изображена зависимость цвета пикселя (в барицентрических координатах) от расстояния до ближайшего пикселя конкретной модели. Из данного примера видно, что малому приращению расстояния до ближайшего полигона может соответствовать скачкообразному изменению в цвете, что приводит к недифференцируемости в классическом смысле.
Проблема №2 (недифференцируемость цвета при сдвигах)
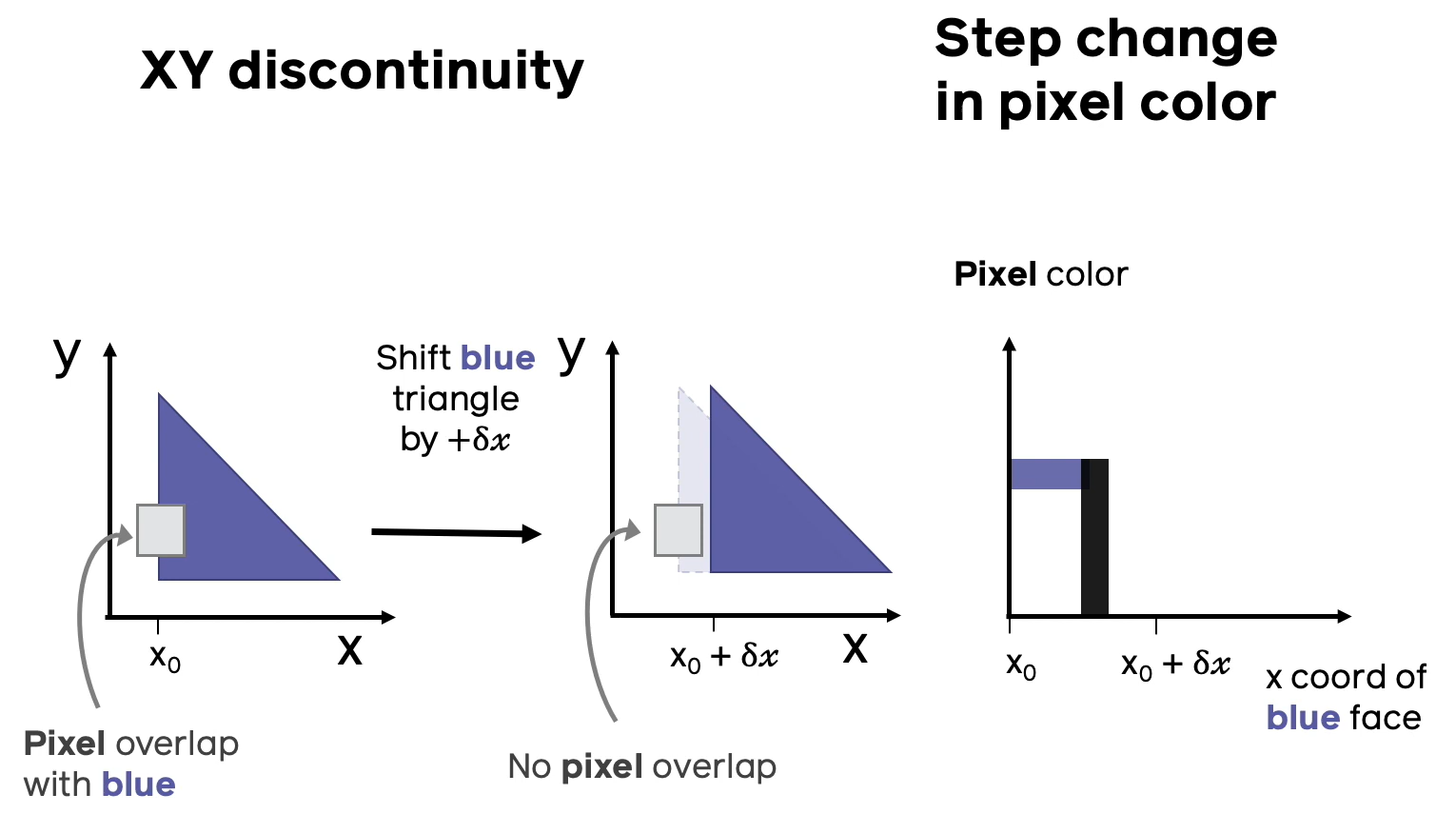
Вторая проблема недифференцируемости аналогична первой, только теперь полигон будет один, а двигать мы его будем не вдоль луча, проходящего через данный пиксель, а в сторону от этого луча. Опять наблюдаем ситуацию, когда малому приращению координаты полигона соответствует скачок в цвете пикселя.
Make it differentiable! — Soft Rasterizer
Процесс рендеринга недифференцируемый, но если бы он таковым являлся, можно было бы решать много актуальных задач в области 3D ML — мы определили проблему, посмотрим как ее можно решить.
Основные подходы к реализации дифференцируемого рендеринга можно проследить в следующей подборке публикаций:
- Loper, M.M. and Black, M.J., 2014, September. OpenDR: An approximate differentiable renderer. In European Conference on Computer Vision (pp. 154-169). Springer, Cham.
- Kato, H., Ushiku, Y. and Harada, T., 2018. Neural 3d mesh renderer. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 3907-3916).
- Li, T.M., Aittala, M., Durand, F. and Lehtinen, J., 2018. Differentiable monte carlo ray tracing through edge sampling. ACM Transactions on Graphics (TOG), 37(6), pp.1-11.
- Liu, S., Li, T., Chen, W. and Li, H., 2019. Soft rasterizer: A differentiable renderer for image-based 3d reasoning. In Proceedings of the IEEE International Conference on Computer Vision (pp. 7708-7717).
- Chen, W., Ling, H., Gao, J., Smith, E., Lehtinen, J., Jacobson, A. and Fidler, S., 2019. Learning to predict 3d objects with an interpolation-based differentiable renderer. In Advances in Neural Information Processing Systems (pp. 9609-9619).
Подходы основаны на разных идеях и приемах. Мы подробно остановимся только на одном, Soft Rasterizer, по двум причинам: во-первых, идея данного подхода математически прозрачна и легко реализуема самостоятельно, во-вторых, данный подход реализован и оптимизирован внутри библиотеки PyTorch 3D [6].
Подробно со всеми аспектами реализации дифференциального рендеринга этим методом можно ознакомиться в соответствующей статье [1], мы же отметим основные моменты.
Для решение проблемы №2, авторы метода предлагают использовать “размытие” границы полигонов, которое приводит к непрерывной зависимости цвета пикселя от координат смещения полигона.

Размытие границ предполагает введение некоторой гладкой вероятностной функции , которая каждой внутренней или внешней точки пространства ставит в соответствие число от 0 до 1 — вероятности принадлежности к данному полигону (чем-то похоже на подход нечеткой логики). Здесь — параметр размытия (чем больше , тем больше размытие), — кратчайшее расстояние в проекционной плоскости от проекции точки до границы проекции полигона (данное расстояние обычно выбирают Евклидовым, но авторы метода отмечают, что здесь есть простор для экспериментов и, например, использование барицентрического расстояния или также подходит для их метода), — функция, которая равна 1 если точка находится внутри полигона и -1 если вне (на границе полигона можно доопределить значение нулем, однако это все равно приводит к тому, что на границе полигона данная функция разрывна, поэтому для точек границ она не применяется), — сигмоидная функция активации, которая часто применяется в глубоком обучении.
Для решения проблемы №1, авторы метода предлагают использовать “смешение” цветов k — ближайших полигонов (blending).
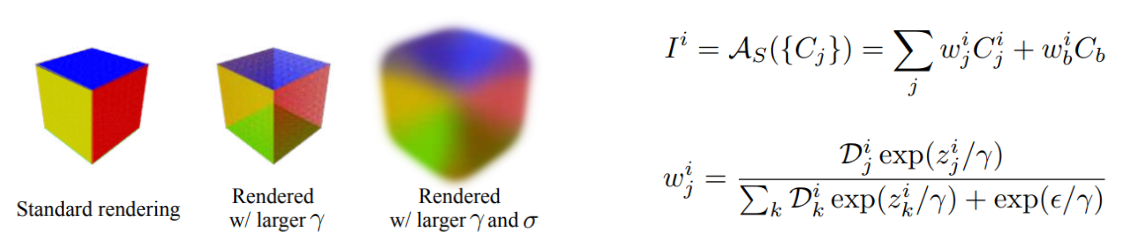
Коротко этот прием можно описать следующим образом: для вычисления итогового цвета -го пикселя , производят нормированное суммирование цветовых карт для k — ближайших полигонов , причем цветовые карты получают путем интерполяции барицентрических координат цвета вершин данных полигонов. Индекс в формуле отвечает за фоновый цвет (background colour), а оператор — оператор агрегирование цвета. — глубина -го пикселя относительно -го полигона, а — параметр смешивания (чем он меньше, тем сильнее превалирует цвет ближайшего полигона).
Итоговой подход Soft Rasterizer, заключается в комбинировании этих двух идей, для одновременного плавного размытия границы и цвета.
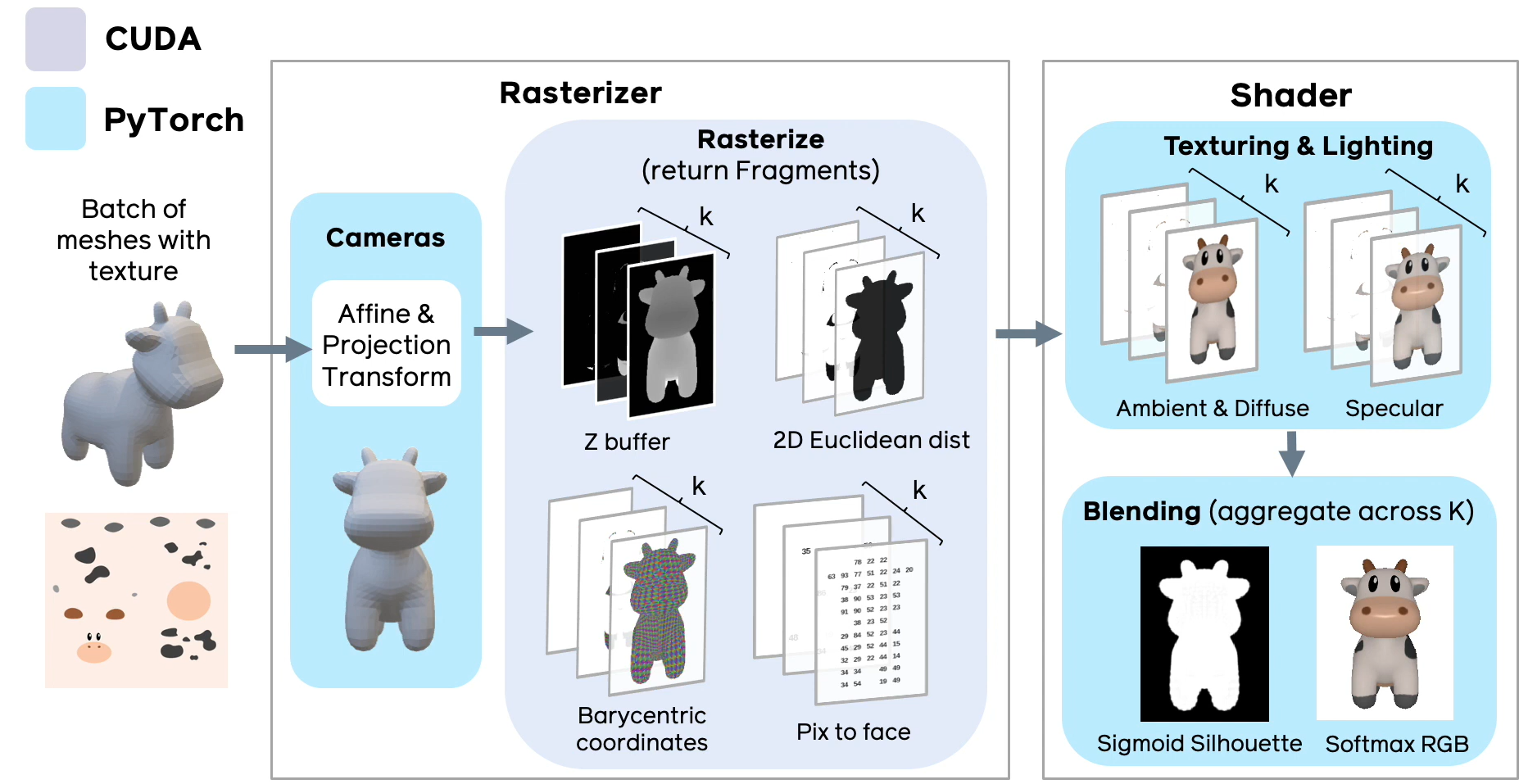
Рис.4 Схема реализации дифференциального рендеринга в PyTorch 3D (слайд из презентации фреймворка).
Реализация Soft Rasterizer внутри библиотеки PyTorch 3D выполнена так, чтобы максимально эффективно и удобно использовать возможности как базового фреймворка PyTorch, так и возможности технологии CUDA. По сравнению с оригинальной реализацией [github page], разработчикам фреймворка удалось добиться 4-х кратного приращения скорости обработки (особенно для больших моделей), при этом возрастает расход памяти за счет того, что для каждого типа данных (ката глубины, карта нормалей, рендер текстур, карта евклидовых расстояний) нужно просчитать k слоев и хранить их в памяти.
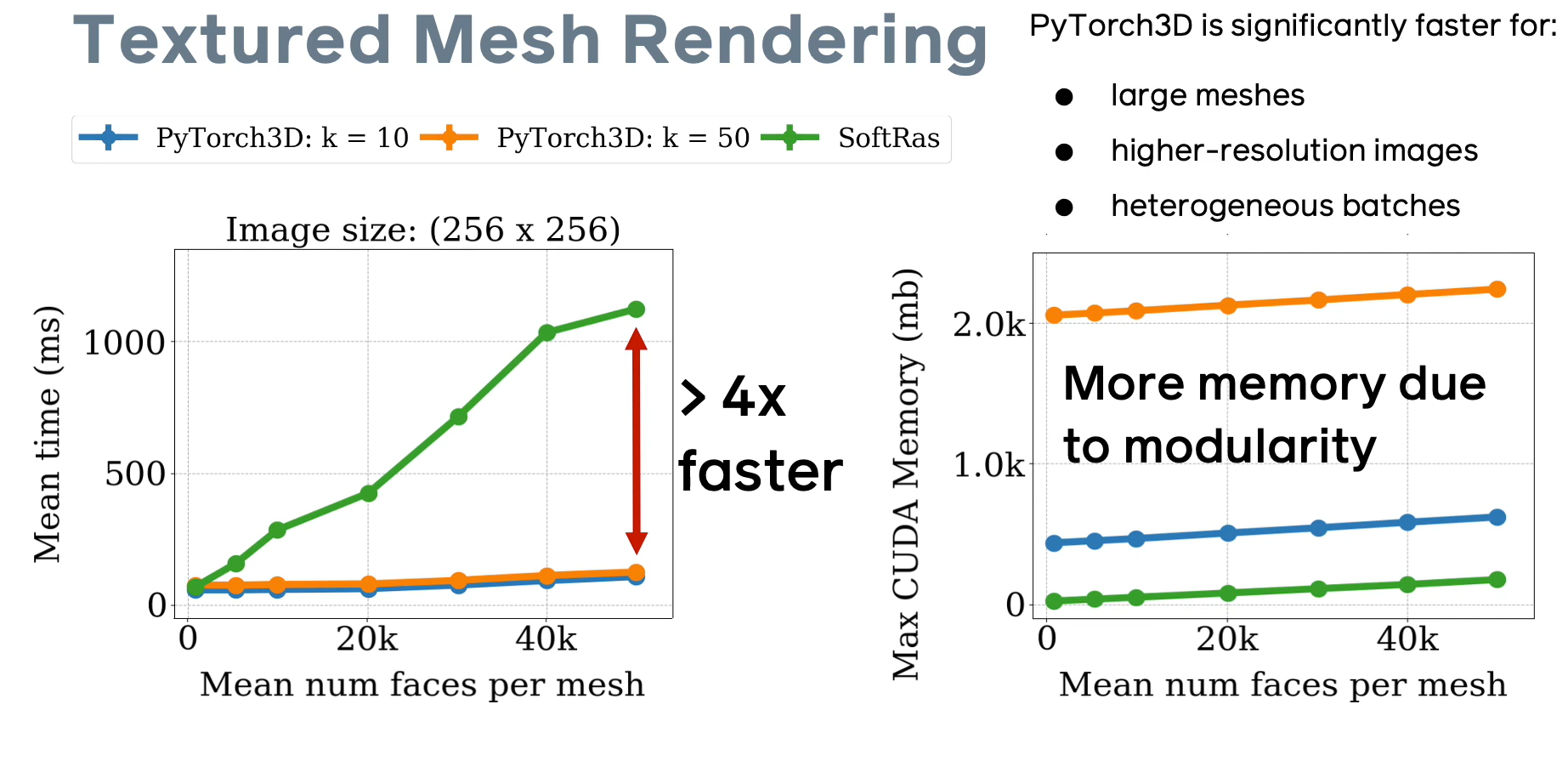
Рис.5 Сравнение характеристик дифференциального рендеринга в PyTorch 3D (слайд из презентации фреймворка).
Поэкспериментировать с настройками дифференциального рендера можно как в PyTorch 3D, так в библиотеке с оригинальной реализацией алгоритма Soft Rasterizer. Давайте рассмотрим пример, демонстрирующий зависимость итоговой картинки отрендеренной модели от параметров дифференциального рендера \sigma, \gamma.
Удобнее всего работать с этой библиотекой в виртуальном окружении anaconda, так как данная библиотека работает уже не с самой актуальной версией pytorch 1.1.0. Также обратите внимание что вам потребуется видеокарта с поддержкой CUDA.
import matplotlib.pyplot as plt
import os
import tqdm
import numpy as np
import imageio
import soft_renderer as sr
input_file = 'path/to/input/file'
output_dir = 'path/to/output/dir'Зададим начальные параметры камеры для рендеринга, загрузим меш объекта с текстурами (есть мод для работы без текстур, в этом случае нужно указать texture_type=’vertex’), инициализируем дифференциальный рендер и создадим директорию для сохранения результатов.
# camera settings
camera_distance = 2.732
elevation = 30
azimuth = 0
# load from Wavefront .obj file
mesh = sr.Mesh.from_obj(
input_file,
load_texture=True,
texture_res=5,
texture_type='surface')
# create renderer with SoftRas
renderer = sr.SoftRenderer(camera_mode='look_at')
os.makedirs(args.output_dir, exist_ok=True)Сначала, посмотрим на нашу модель с разных сторон и для этого отрендерим анимацию пролета камеры по кругу с помощью рендера.
# draw object from different view
loop = tqdm.tqdm(list(range(0, 360, 4)))
writer = imageio.get_writer(
os.path.join(output_dir, 'rotation.gif'),
mode='I')
for num, azimuth in enumerate(loop):
# rest mesh to initial state
mesh.reset_()
loop.set_description('Drawing rotation')
renderer.transform.set_eyes_from_angles(
camera_distance,
elevation,
azimuth)
images = renderer.render_mesh(mesh)
image = images.detach().cpu().numpy()[0].transpose((1, 2, 0))
writer.append_data((255*image).astype(np.uint8))
writer.close()Теперь поиграемся со степенью размытия границы и степенью смешения цветов. Для этого будем в цикле увеличивать параметр размытия и одновременно увеличивать параметр смешения цвета .
# draw object from different sigma and gamma
loop = tqdm.tqdm(list(np.arange(-4, -2, 0.2)))
renderer.transform.set_eyes_from_angles(camera_distance, elevation, 45)
writer = imageio.get_writer(
os.path.join(output_dir, 'bluring.gif'),
mode='I')
for num, gamma_pow in enumerate(loop):
# rest mesh to initial state
mesh.reset_()
renderer.set_gamma(10**gamma_pow)
renderer.set_sigma(10**(gamma_pow - 1))
loop.set_description('Drawing blurring')
images = renderer.render_mesh(mesh)
image = images.detach().cpu().numpy()[0].transpose((1, 2, 0))
writer.append_data((255*image).astype(np.uint8))
writer.close()
# save to textured obj
mesh.reset_()
mesh.save_obj(
os.path.join(args.output_dir, 'saved_spot.obj'),
save_texture=True)Итоговый результат на примере стандартной модели текстурированной коровы (cow.obj, cow.mtl, cow.png — удобно скачивать, например, с помощью wget) выглядит так:

Neural rendering

Дифференциальный рендеринг как базовый инструмент для 3D ML, позволяет создавать очень много интересных архитектур глубокого обучения в области, которая получила названия нейронный рендеринг (neural rendering). Нейронный рендеринг позволяет решать множество задач, связанных с процедурой рендеринга: от добавления новых объектов на фото и в видеопоток до сверхбыстрого текстурирования и рендеринга сложных физических процессов.
Сегодня мы оставим приложение дифференциального рендеринга к конструированию нейронного рендеринга за скобками повествования, однако порекомендуем всем заинтересовавшимся следующие источники:
- большая обзорная статья SOTA архитектур в области нейронного рендеринга [7] на основе прошедшей CVPR 2020;
- видео с записью утренней и дневной сессией по нейтронному рендерингу с CVPR 2020, на основе которых и была написана статья из предыдущего пункта;
- видеолекция MIT DL Neural rendering с кратким обзором основных подходов и введении в тему;
- заметка на Medium на тему дифференциального рендеринга и его приложений;
- видео с youtube канала two minute papers на данную тему.
Experiment: Mona Liza reconstruction
Разберем пример применения дифференциального рендеринга для восстановления параметров 3D сцены по исходному изображению человеческого лица, представленный в пуле примеров библиотеки redner, которая является реализацией идей, изложенных в статье [ 4 ].
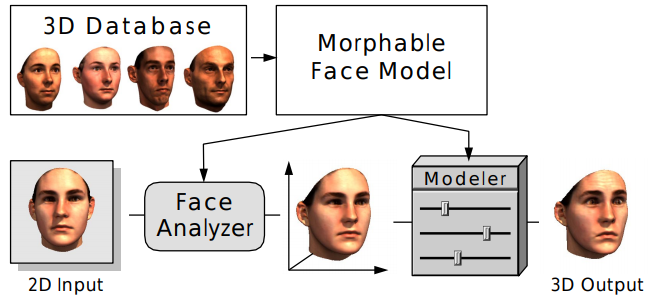
В данном примере, мы будем использовать т.н. 3D morphable model [8] — технику текстурированного трехмерного моделирования человеческого лица, ставшую уже классической в области анализа 3D. Техника основана на получение такого крытого представления признаков 3D данных, которое позволяет строить линейные комбинации, сочетающие физиологические особенности человеческих лиц (если так можно выразиться, то это своеобразный Word2Vec от мира 3D моделирования человеческих лиц).
Для работы с примером вам потребуется датасет Basel face model (2017 version). Файл model2017-1_bfm_nomouth.h5 необходимо будет разместить в рабочей директории вместе с кодом.
Для начала загрузим необходимы для работы библиотеки и датасет лиц.
import torch
import pyredner
import h5py
import urllib
import time
from matplotlib.pyplot import imshow
%matplotlib inline
import matplotlib.pyplot as plt
from IPython.display import display, clear_output
from matplotlib import animation
from IPython.display import HTML# Load the Basel face model
with h5py.File(r'model2017-1_bfm_nomouth.h5', 'r') as hf:
shape_mean = torch.tensor(hf['shape/model/mean'],
device = pyredner.get_device())
shape_basis = torch.tensor(hf['shape/model/pcaBasis'],
device = pyredner.get_device())
triangle_list = torch.tensor(hf['shape/representer/cells'],
device = pyredner.get_device())
color_mean = torch.tensor(hf['color/model/mean'],
device = pyredner.get_device())
color_basis = torch.tensor(hf['color/model/pcaBasis'],
device = pyredner.get_device())Модель лица в таком подходе разделена отдельно на базисный вектор формы — shape_basis (вектор длины 199 полученный методом PCA), базисный вектор цвета — color_basis (вектор длины 199 полученный методом PCA), также имеем усредненный вектор формы и цвета — shape_mean, color_mean. В triangle_list хранится геометрия усредненного лица в форме полигональной модели.
Создадим модель, которая на вход будет принимать векторы скрытого представления цвета и формы лица, параметры камеры и освещения в сцене, а на выходе будет генерировать отрендеренное изображение.
indices = triangle_list.permute(1, 0).contiguous()
def model(
cam_pos,
cam_look_at,
shape_coeffs,
color_coeffs,
ambient_color,
dir_light_intensity):
vertices = (shape_mean + shape_basis @ shape_coeffs).view(-1, 3)
normals = pyredner.compute_vertex_normal(vertices, indices)
colors = (color_mean + color_basis @ color_coeffs).view(-1, 3)
m = pyredner.Material(use_vertex_color = True)
obj = pyredner.Object(vertices = vertices,
indices = indices,
normals = normals,
material = m,
colors = colors)
cam = pyredner.Camera(position = cam_pos,
# Center of the vertices
look_at = cam_look_at,
up = torch.tensor([0.0, 1.0, 0.0]),
fov = torch.tensor([45.0]),
resolution = (256, 256))
scene = pyredner.Scene(camera = cam, objects = [obj])
ambient_light = pyredner.AmbientLight(ambient_color)
dir_light = pyredner.DirectionalLight(torch.tensor([0.0, 0.0, -1.0]),
dir_light_intensity)
img = pyredner.render_deferred(scene = scene,
lights = [ambient_light, dir_light])
return imgТеперь посмотрим как выглядит усредненное лицо. Для этого зададим первоначальные параметры освещения и позиции камеры и воспользуемся нашей моделью. Также загрузим целевое изображение, параметры которого мы хотим восстановить и взглянем на него:
cam_pos = torch.tensor([-0.2697, -5.7891, 373.9277])
cam_look_at = torch.tensor([-0.2697, -5.7891, 54.7918])
img = model(cam_pos,
cam_look_at,
torch.zeros(199, device = pyredner.get_device()),
torch.zeros(199, device = pyredner.get_device()),
torch.ones(3),
torch.zeros(3))
imshow(torch.pow(img, 1.0/2.2).cpu())
face_url = 'https://raw.githubusercontent.com/BachiLi/redner/master/tutorials/mona-lisa-cropped-256.png'
urllib.request.urlretrieve(face_url, 'target.png')
target = pyredner.imread('target.png').to(pyredner.get_device())
imshow(torch.pow(target, 1.0/2.2).cpu())
Зададим начальные значения параметров, которые будем пытаться восстановить для целевой картины.
# Set requires_grad=True since we want to optimize them later
cam_pos = torch.tensor([-0.2697, -5.7891, 373.9277],
requires_grad=True)
cam_look_at = torch.tensor([-0.2697, -5.7891, 54.7918],
requires_grad=True)
shape_coeffs = torch.zeros(199, device = pyredner.get_device(),
requires_grad=True)
color_coeffs = torch.zeros(199, device = pyredner.get_device(),
requires_grad=True)
ambient_color = torch.ones(3, device = pyredner.get_device(),
requires_grad=True)
dir_light_intensity = torch.zeros(3, device = pyredner.get_device(),
requires_grad=True)
# Use two different optimizers for different learning rates
optimizer = torch.optim.Adam(
[
shape_coeffs,
color_coeffs,
ambient_color,
dir_light_intensity],
lr=0.1)
cam_optimizer = torch.optim.Adam([cam_pos, cam_look_at], lr=0.5)Остается организовать, оптимизационный цикл и логировать происходящее с функцией ошибки (в нашем случае это попиксельный MSE + квадратичные регуляризаторы параметров) и с самой 3D моделью.
plt.figure()
imgs, losses = [], []
# Run 500 Adam iterations
num_iters = 500
for t in range(num_iters):
optimizer.zero_grad()
cam_optimizer.zero_grad()
img = model(cam_pos, cam_look_at, shape_coeffs,
color_coeffs, ambient_color, dir_light_intensity)
# Compute the loss function. Here it is L2 plus a regularization
# term to avoid coefficients to be too far from zero.
# Both img and target are in linear color space,
# so no gamma correction is needed.
loss = (img - target).pow(2).mean()
loss = loss
+ 0.0001 * shape_coeffs.pow(2).mean()
+ 0.001 * color_coeffs.pow(2).mean()
loss.backward()
optimizer.step()
cam_optimizer.step()
ambient_color.data.clamp_(0.0)
dir_light_intensity.data.clamp_(0.0)
# Plot the loss
f, (ax_loss, ax_diff_img, ax_img) = plt.subplots(1, 3)
losses.append(loss.data.item())
# Only store images every 10th iterations
if t % 10 == 0:
# Record the Gamma corrected image
imgs.append(torch.pow(img.data, 1.0/2.2).cpu())
clear_output(wait=True)
ax_loss.plot(range(len(losses)), losses, label='loss')
ax_loss.legend()
ax_diff_img.imshow((img -target).pow(2).sum(dim=2).data.cpu())
ax_img.imshow(torch.pow(img.data.cpu(), 1.0/2.2))
plt.show()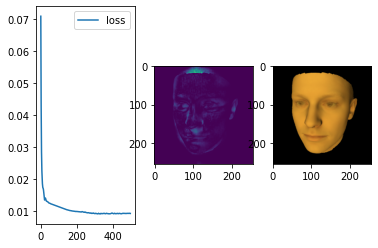
Чтобы лучше понимать что происходило со сценой в процессе обучения можем сгенерировать анимацию из наших логов:
fig = plt.figure()
# Clamp to avoid complains
im = plt.imshow(imgs[0].clamp(0.0, 1.0), animated=True)
def update_fig(i):
im.set_array(imgs[i].clamp(0.0, 1.0))
return im,
anim = animation.FuncAnimation(fig, update_fig,
frames=len(imgs), interval=50, blit=True)
HTML(anim.to_jshtml())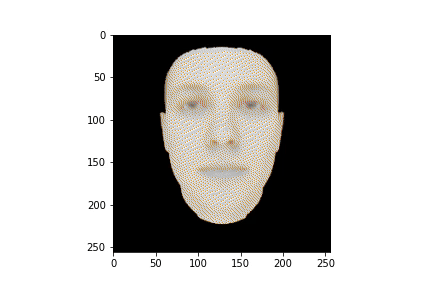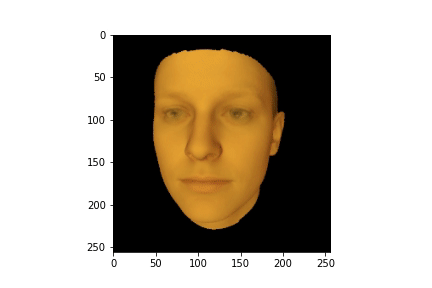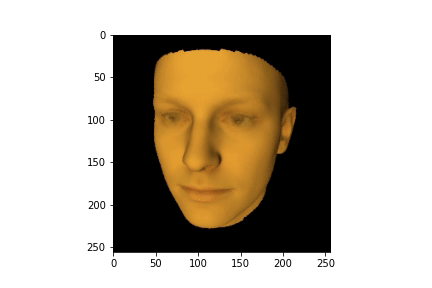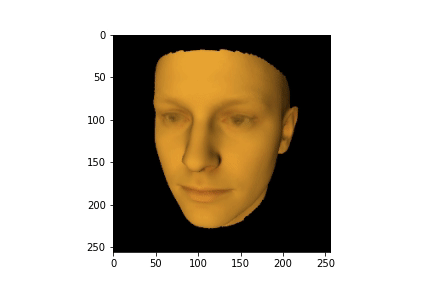
Conclusions
Дифференциальный рендеринг — новое интересное и важное направление на стыке компьютерной графики, компьютерного зрения и машинного обучения. Данная технология стала основой для многих архитектур в области нейронного рендеринга, который в свою очередь расширяет границы возможностей компьютерной графики и машинного зрения.
Существуют несколько популярных библиотек глубокого вычисления (например Kaolin, PyTorch 3D, TensorFlow Graphics), которые содержат дифференциальный рендеринг как составную часть. Также существуют отдельные библиотеки, реализующие функционал дифференциального рендеринга (Soft Rasterizer, redner). С их помощью можно реализовывать множество интересных проектов, вроде проекта с восстановлением параметров лица и текстуры портрета человека.
В ближайшем будущем, мы можем ожидать появление новых техник и библиотек для дифференциального рендеринга и их применения в области нейронного рендеринга. Возможно, уже завтра может появится способ делать реалистичную графику в реальном времени или генерировать 2D и 3D контент приемлемого для людей качества с помощью этой технологии. Мы будем следить за развитием этого направления и постараемся рассказывать о всех новинках и интересных экспериментах.
- Liu, S., Li, T., Chen, W. and Li, H., 2019. Soft rasterizer: A differentiable renderer for image-based 3d reasoning. In Proceedings of the IEEE International Conference on Computer Vision (pp. 7708-7717). [ paper ]
- Loper, M.M. and Black, M.J., 2014, September. OpenDR: An approximate differentiable renderer. In European Conference on Computer Vision (pp. 154-169). Springer, Cham. [ paper ]
- Kato, H., Ushiku, Y. and Harada, T., 2018. Neural 3d mesh renderer. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 3907-3916). [ paper ]
- Li, T.M., Aittala, M., Durand, F. and Lehtinen, J., 2018. Differentiable monte carlo ray tracing through edge sampling. ACM Transactions on Graphics (TOG), 37(6), pp.1-11. [ paper ]
- Chen, W., Ling, H., Gao, J., Smith, E., Lehtinen, J., Jacobson, A. and Fidler, S., 2019. Learning to predict 3d objects with an interpolation-based differentiable renderer. In Advances in Neural Information Processing Systems (pp. 9609-9619). [ paper ]
- Ravi, N., Reizenstein, J., Novotny, D., Gordon, T., Lo, W.Y., Johnson, J. and Gkioxari, G., 2020. Accelerating 3D Deep Learning with PyTorch3D. arXiv preprint arXiv:2007.08501. [ paper ] [ github ]
- Tewari, A., Fried, O., Thies, J., Sitzmann, V., Lombardi, S., Sunkavalli, K., Martin-Brualla, R., Simon, T., Saragih, J., Nie?ner, M. and Pandey, R., 2020. State of the Art on Neural Rendering. arXiv preprint arXiv:2004.03805. [ paper ]
- Blanz, V. and Vetter, T., 1999, July. A morphable model for the synthesis of 3D faces. In Proceedings of the 26th annual conference on Computer graphics and interactive techniques (pp. 187-194). [ paper ][ project page ]

