В посте есть результаты экспериментов с различными биологическими и физическими закономерностями, в частности песочный сплайн, дифференциальная решетка, песчаные творения и песочные знаки.

Это развитие идей из публикаций:

Визуализация при помощи генеративных алгоритмов: гифа, деревья, повторяющиеся и дифференциальные линии (на Python)

Визуализация при помощи генеративных алгоритмов: дифференциальная сетка (2D и 3D) и трещины

Однако вам необязательно читать их — все проекты, описанные здесь самодостаточны.

ПЕСОЧНЫЙ СПЛАЙН [GITHUB]

Идею песочного сплайна я почти отбросил, потому что мне казалось, что это не даст никаких интересных результатов. Тем не менее, я дал ей шанс, и в итоге остался очень доволен.



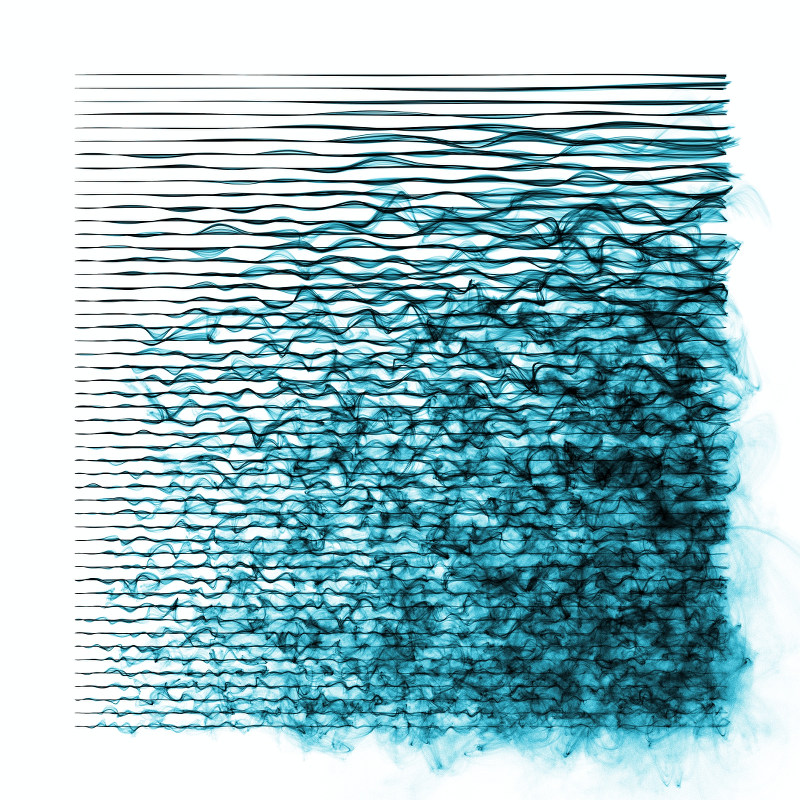
Идея основана на концепции B-сплайнов. В математике B-сплайн представляет собой плавную кривую, которая нарисована из ряда узлов (контрольных точек) без обязательного прохождения через сами эти узлы. Если вы переместите немного узлы, плавная кривая кривая будет следовать дальше. И если вы заставите узлы потихоньку двигаться, сплайн постепенно станет все более рассеянным. Вы можете увидеть это в анимации ниже.



В этой анимации сплайн начинается справа и движется против часовой стрелки. Вы также можете заметить, чем дальше вдоль сплайна, тем больше становится уровень шума. Это не имеет ничего общего с самим сплайном, но это хороший способ сохранить исходный узел в начальном положении.

Вместо того, чтобы просто рисовать сплайн, я рисую ряд прозрачных точек вдоль линии в каждой итерации. Ещё я рисую одинаковое количество точек каждый раз, независимо от длины линии. Так как движение постепенное, высокая плотность образуется там, где линия движется медленно, а более низкая там, где линия движется быстро.

Такое поведение, и техника рисования, во многом похожи на несколько работ Тарбелла, в том числе Sand Dollar, Limb Sand Stroke, Sand traveller и Sandstroke. Отсюда и пошло название. Несколько человек указали мне, что эти образы также очень напоминают Аттрактор Лоренца, хотя метод используется немного другой.



Сочетание этого простого метода с различными конфигурациями сплайнов и цветов даёт огромное количество вариаций результатов, и я, вероятно, вернусь к экспериментам с ней в будущем.

ДИФФЕРЕНЦИАЛЬНАЯ РЕШЁТКА [GITHUB]

При работе над дифференциальной линией, дифференциальной сеткой и дифференциальной сеткой в 3d наиболее утомительной частью было управление структурой данных. Отчасти потому что я решил научиться использовать half-edge структуры данных в этом процессе. И ещё потому что это у меня так и не получилось. И, наконец, потому что я писал его в Cython, который был в новинку для меня.

Несмотря на всё это, я получил нормальный результат. Тем не менее, этот процесс также привёл меня к желанию создать более слабо соединённую систему. Мне казалось, что такой системой будет легче управлять. Ещё у меня была мысль, что такая система может быть похожа на слизистую плесень, так же как дифференциальная сетка более или менее похожа на лишайник.

Держа это в голове, я начал создавать дифференциальные решетки. Часть алгоритма очень похожа на дифференциальную сетку. Он состоит из соединённых узлов, и соединённые узлы пытаются оставаться близко друг к другу. Он также сохраняет принцип, когда каждый узел пытается избежать близости со всеми несвязанными узлами в определенном радиусе. Важная особенность в том, что соединения между узлами перерассчитываются перед каждой итерацией. Это означает, что нам нужен хороший способ решить, должны ли два близлежащих узла считаться соседями или нет.

Оказывается, что относительные окрестности хорошо подходят для этого. Несколько упрощённо можно сказать, что два узла являются относительными соседями, если достаточно большая область между двумя узлами не содержит других узлов.



Еще одна вещь, которую нужно рассмотреть в этой системе, это то, как вводятся новые узлы. В дифференциальной сетке новые узлы вводятся путем разделения краев пополам. Это один из сложных процессов half-edge структуры данных. Особенно, если вы упрямо вводили свою собственную версию структуры данных, как и я. В слабо связанной системе, такой как дифференциальная решетка, добавление нового узла — это решение позиции, ввод узла и пересчитывание соседства, как это было бы на любом этапе моделирования.

Благодаря этому вся задача сводится к решению, куда разместить новые узлы, и как часто новые узлы должны появляться. В этих примерах новые узлы появляются в областях, где локальная плотность узлов достаточно низка. Это приводит к тому, что новые узлы часто появляются за пределами существующей структуры. Получается что-то наподобие слизистой плесени, которая постепенно растет наружу.

Эта система не имеет какого-либо распределения источников пищи (точек, которые ускоряют рост), что является интересным аспектом для изучения. Например, такая простая система каким-то образом сможет в теории повторить Токийскую железнодорожную систему или показать какое-нибудь другое интересное поведение (но это не точно).



Эта система реализована с помощью pyCUDA, что означает, что все расчеты расстояний и расчёты соседства могут быть сделаны на GPU. Поэтому это, вероятно, один из самых быстрых алгоритмов, которые я когда-либо реализовывал. Можно сделать системы с сотнями тысяч узлов удивительно быстро, с учетом количество вычислений.

Ниже изображение с около 80 000 узлами, которое было нарисовано на моём механическом плоттере.



ПЕСЧАНЫЕ ТВОРЕНИЯ [GITHUB]

При работе над песочными сплайнами у меня получились несколько промежуточных результатов, которые напомнили мне текст, написанный от руки/ Вместо того, чтобы напрямую пытаться сделать что-то, что выглядело бы как написанный текст, я начал экспериментировать с генерацией малых «Песчаных творений».

Я попробовал несколько разных подходов, но следующий метод привел к наиболее приятным результатам:

• Создать несколько случайных контрольных точек из равномерного распределения, ограниченного сферой.
• Расположить их в произвольном порядке.
• Создать B-сплайн из контрольных точек в том же порядке.

Для того, чтобы добавить текстуру к формам, я делаю еще один сплайн путём клонирования первого набора контрольных точек, и немного перемещая все наугад. Потом я использую ранее упомянутую sandstroke технику, чтобы нарисовать прямые линии между одинаково расположенными точками на двух сплайнах. Таким образом, получается хорошая зернистость.

С небольшими изменениями параметров можно получить совершенно разные результаты, как например в примере ниже.



Текстура на этих изображениях выглядит гораздо лучше при крупной печати. К сожалению, на данный момент такая печать недоступна. Вместо этого вы можете взглянуть на это изображение более высокого качества, прежде чем перейти к следующему разделу.

ПЕСЧАНЫЕ ЗНАКИ [GITHUB]

После того как я опубликовал нескольких своих Песчаных Творений, мне предложили попробовать сделать свой шрифт. Я не пробовал сделать это ранее, но зато пробовал различные методы создания написанного от руки текста, путем объединения нескольких песчаных творений, из предыдущего раздела. Как вы можете видеть ниже, даже очень простые комбинации песчаных творений могут создать довольно приятное асемическое письмо.

Чтобы получить представление о том, как это работает, вы можете посмотреть на изображение ниже, где выделены контрольные точки.



Есть ряд вещей, с которыми можно поэкспериментировать даже в этой простой конфигурации:

• Количество контрольных точек на знак;
• Расстояние между знаками;
• Форма знаков;
• Положение знаков относительно горизонтальной центральной линии;
• Внутренний порядок контрольных точек в знаках;
• Количество знаков в слове;
• Как письмо делится на строки;
• И так далее ...

Не говоря уже о том, что все эти вещи предполагают написанный слева направо, более или менее латинский, написанный от руки текст.

Ниже приведен пример одной из конфигураций, которую считаю лучшей до сих пор.



Есть ещё такое видео того, как мой плоттер выписывает текст.

Наконец, я хотел бы обратить ваше внимание на Lettres de ma mere, сделанную пионером генеративного искусства Верой Мольнар.

Больше работ автора можно увидеть на сайте Inconvergent

Предыдущие проекты этого же автора:

• Визуализация при помощи генеративных алгоритмов: гифа, деревья, повторяющиеся и дифференциальные линии (на Python)
• Визуализация при помощи генеративных алгоритмов: дифференциальная сетка (2D и 3D) и трещины

А если генеративное искусство и визуализация данных, вас заинтересовали — посмотрите другие посты degenerative_art, вот самые популярные на данный момент:

• Как заставить генеративные изображения выглядеть естественно при помощи математических алгоритмов
• Красивая и подробная геологическая карта Марса, сделанная на Python, GDAL
• Создание эффекта быстрого полета сквозь космос (или падающего снега) за 10 минут на p5.js