Как создавать необычно красивые линии? Изучаем поле течений / forpes.ru

Главная
Как создавать необычно красивые линии? Изучаем поле течений

Как создавать необычно красивые линии? Изучаем поле течений +45

18.11.2020 10:43

degenerative_art 7 4000 Источник

Поля течения - невероятно мощный и гибкий инструмент для создания необычных линий. Это один из основных инструментов, который я несколько лет использовал в моих генеративных произведениях, и я осознаю, что обращаюсь к нему снова и снова. Вполне возможно, что я использовал его столько раз при написании кода, сколько не использовал никто другой.

Также поля течения - то, на что программисты натыкаются в первую очередь, когда только начинают заниматься генеративным искусством, но немногие уделяют время детальному изучению принципов их работы и тому, как их можно использовать. В этой статье я освечу основы полей течения, предложу разные варианты их использования и дам советы как сделать из них что-то красивое.

Сетка углов

Поля течения основаны на сетке (grid). Грубо говоря, сетка покрывает всю картину. В каждой точке сетки хранится угол. Сетка должна храниться в виде 2D массива чисел с плавающей запятой. Каждая единица в сетке хранит значение угла и одновременно представляет собой точку на сетке.

При созданию сетки надо выбрать ее разрешение. Другими словами, расстояние между точками в сетке. Чем выше разрешение, тем мельче детали, которые вы можете проработать, и плавнее линии. Недостатком является то, что может пострадать функциональность, если увеличите его слишком сильно. Обычно я использую около 0.5% ширины изображения в качестве расстояния между точками. Ещё я использую ту же длину для длины пространства между точками, чтобы упростить расчёты и избежать ошибок точности плавающей запятой.

Последняя настройка, над которой надо подумать - это границы сетки. Вам, наверно, захочется сделать их такими же, как границы самой картина или кадра. Я понял, что лучше делать их ещё больше. Иногда намного больше. Зачем? Если линии выходят за пределы изображения, то это лучше, чем если они просто пропадают. Мне нравится иметь возможность их поворачивать в пределах изображения. Ещё иногда лучше работает, если начинать линии за границами картины и давать им «влиться» в неё.

Предположим, что перед нами картина 1000 x 1000 пикселей, и мы хотим залить ещё 50% площади вне ее границ. Мы можем установить нашу сетку вот так (псевдокод):

left_x = int(width * -0.5)
right_x = int(width * 1.5)
top_y = int(height * -0.5)
bottom_y = int(height * 1.5) 
resolution = int(width * 0.01) 
num_columns = (right_x - left_x) / resolution
num_rows = (bottom_y - top_y) / resolution
grid = float[num_columns][num_rows]
default_angle = PI * 0.25
for (column in num_columns) {
    for (row in num_rows) {
        grid[column][row] = default_angle
    }
}

Если бы мы запустили программу для визуализации кода этой сетки в таком виде, то это выглядело бы приблизительно так (качество отрегулировано для лучшей видимости).

Стандартная сетка со всеми углами, установленными на pi* 0.25

Теперь у нас есть поле, с которым можно работать. Но к сожалению, пока будут рисоваться только прямые линии. Поработаем над этим. Пока давайте заставим сетку проворачиваться в процессе изменения положения точек на картине.

for (column in num_columns) {
     for (row in num_rows) {
         angle = (row / float(num_rows)) * PI
         grid[column][row] = angle
     }
}

Это выглядит как-то так:

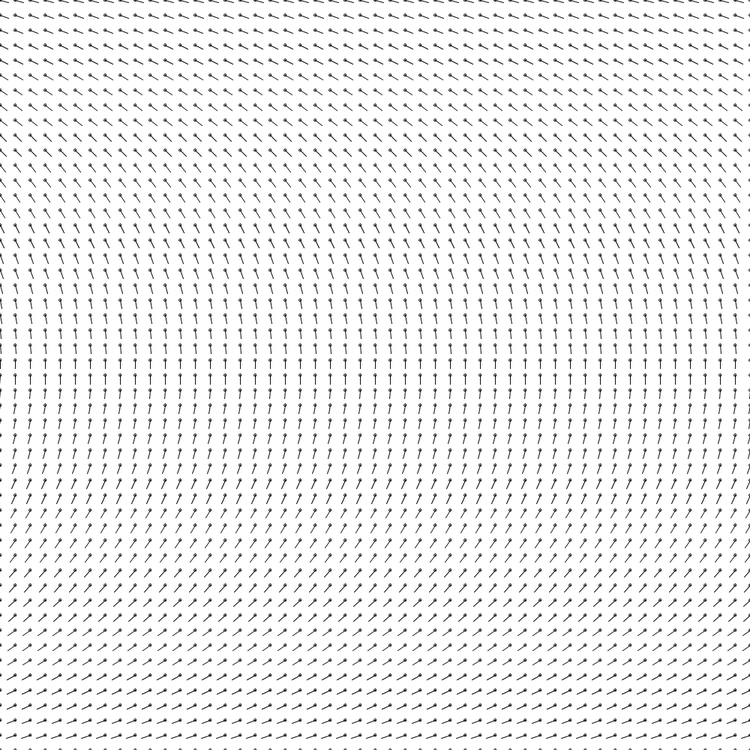
Рисование кривых линий через поле

Теперь мы используем сетку для рисования линий. Вот базовый алгоритм: выбираем начальную точку. Находим подходящую точку рядом на сетке. Берём угол с этой точки на сетке и делаем небольшой «шаг» в сторону этого угла. На новом месте мы снова делаем поиск и повторяем предыдущие шаги раз за разом. Выглядит это так (псевдокод).

// starting point
x = 500
y = 100
begin_curve()
for (n in [0..num_steps]) {
    draw_vertex(x, y)
    x_offset = x - left_x
    y_offset = y - top_y
    column_index = int(x_offset / resolution)
    row_index = int(y_offset / resolution)
    // ПРИМЕЧАНИЕ: обычно на этом этапе стоит проверить границы
    grid_angle = grid[column_index][row_index]
    x_step = step_length * cos(grid_angle)
    y_step = step_length * sin(grid_angle)
    x = x + x_step
    y = y + y_step
}
end_curve()

Если мы это проделаем только для одной кривой, это будет выглядеть как-то так:

Рисование единственной простой кривой на поле

Нам нужно выбрать значения для нескольких ключевых параметров для рисования линий: step_length, num_steps, и starting position (x, y). Step_length - самый простой параметр. Как правило, он должен быть настолько мал, чтобы нельзя было увидеть никаких резких углов на кривой линии. Как по мне, он должен быть около 0.1%-0.5% ширины картины. Я делаю больше, если мне нужен более быстрый рендеринг, и меньше, если есть углы, которые надо подкорректировать. Другие переменные требуют больше разъяснений.

num_steps

Значение num_steps повлияет на текстуру результата. Небольшие линии могут выглядеть более «пушистыми». Длинные - более «жидкими». Вот пример одного и того же кода, выполняемого с разными значениями num_steps. Для начала, с короткими линиями:

И теперь с длинными:

Обратите внимание, как резко выглядят линии на первой картине и как плавно на второй. На первой картине можно увидеть отдельные пятна светлых и тёмных оттенков, но все выглядит более системно и уравновешено. На второй картине больше видимых длинных линий, по которым следует взгляд и которые как бы «разламывают» всю картину.

Следующий вопрос, требующий ответа - собираетесь ли вы смешивать цвета. Короткие линии сохраняют цвет изолировано, отдельно от других, а длинные - вливают цвет в участки другого цвета. Когда я использую много цветов, то обычно выбираю короткие или средние линии, чтобы избежать создания участков, где цвета слишком сильно смешиваются.

С другой стороны, если я использую близкие цвета, то работа с длинными линиями в самый раз. Посмотрите на задний план: здесь используются лишь едва отличающиеся кремовые цвета.

starting_point

Все кривые линии должны где-то начинаться. Обычно я использую один из трёх вариантов выбора начальной позиции:

Использовать стандартную сетку для начальных позиций
Использовать единообразный случайный выбор точек
Использовать круговую укладку

Стандартная сетка - самый простой вариант, но иногда она может быть слишком негибкой. Единообразно случайный выбор кажется лучше, но он сделает некоторые места либо слишком загромождёнными, либо пустыми, а это не всегда то, что нужно. Подход круговой укладки самый сбалансированный: всё достаточно хорошо распределено и с достаточной рандомностью, из-за чего выглядит более «расслаблено». Эти различия еле заметны, если рисовать просто длинные линии без цвета или других особенностей:

Сетка - Случайный выбор - Круговая укладка

Но если укоротить линии, разница станет очевидной.

Поля течения могут быть очень важны для некоторых дизайнерских решений, поэтому рекомендую изучить эту тему внимательно. Также вам может быть интересно поэкспериментировать с базовыми установками, например, изменить изначальный размер залития картины, начать с краев или середины и т.п.

Деформация векторов

Важная дизайнерская дилемма: каким образом деформировать векторы в поле. Выбранный способ определит форму искривлений. Определит, будут ли это завитки, резкие повороты или накладывающиеся друг на друга линии.

Шум Перлина

В 90% случаев шум Перлина используется для отстройки векторов. Это удобно и просто, ибо даёт гладкие и продолжительные значения параметров по всей 2D плоскости. Есть ещё разные параметры шума - их множество от значимых до почти не влияющих на итоговую картину. Все это очень легко использовать в Processing. Функция noise() задает значения шума Перлина (между 0,0 и 1,0) с учётом координат.

Вернувшись к коду, мы вместо вставки default_angle можем сделать что-то такое:

for (column in num_columns) {
  for (row in num_rows) {
      //noise() в // Processing работает лучше всего в середине
      // точки примерно 0.005, поэтому уменьшаем до
      scaled_x = column * 0.005
      scaled_y = row * 0.005
      // получаем наше значение шума между 0,0 и 0,1
      noise_val = noise(scaled_x, scaled_y)
      // перенести значение шума к углу (между 0 0 2 * PI)
      angle = map(noise_val, 0.0, 1.0, 0.0, PI * 2.0)
      grid[column][row] = angle
  }
}

Вам нужно будет поиграть с опцией noiseDetail() и с параметрами масштабирования значения шума к углам, чтобы получить нужный вам эффект.

Как бы то ни было, я рекомендую придумать собственный способ деформации векторов, а не полагаться на шум Перлина, ибо он слишком явный и массовый. Но есть ещё один инструмент, о котором лучше знать или начинать с него.

Непродолжающиеся деформации

Важный аттрибут для деформации, который вы можете задать - это будет ли деформация продолжающейся или нет. Под продолжающейся я имею в виду плавный переход между соседними векторами, без «прыжков» Как я уже упоминал, шум Перлина как раз так и работает. У меня есть своя техника деформации, у которой есть это качество, и которую я люблю использовать. Когда вы используете продолжающуюся деформацию, кривые не пересекают друг друга, они плавные и систематизированные. Однако стоит поэкспериментировать ещё и с непродолжающейся деформацией векторов. Простой пример, как это можно сделать, - начать с шума Перлина, но округлить угол каждого вектора до pi/10:

Так мы получим более скульптурные, каменистые формы. Если увеличим до pi/4, то результат станет странным:

Как вариант, можно выбрать случайный угол (между 0 и pi) для каждого ряда векторов:

Или выбрать случайный угол для каждого вектора.

Суть в том, что и непродолжающиеся деформации тоже могут генерировать хорошие штуки.

Сочетание с другими техниками

Существует бесконечное множество способов экспериментов с полями течения и использования их по-новому. Вот несколько вещей, опробованных мною, вам для вдохновения.

Можно установить минимально возможное расстояние между кривыми. На каждой стадии кривой проверяйте, не слишком ли близко другая линия. Если близко, то останавливайтесь. Я использовал эту технику на зеркальном рисунке в 2019 году:

Можно нарисовать точки на месте продолжающихся деформаций. Если вы настроите проверку и избежите коллизий, то сможете получить что-то крутое:

Можно слегка деформировать сетку между циклами рисования. Это немного изменит линии, которые вы получаете, предоставляя вам разнообразие и накладывающиеся друг на друга линии без полного изменения всей картины:

Можно делать переход между соседними линиями для создания контура многоугольника. Если интерполировать между двумя соседями (возможно, с нелинейным ослаблением), то можно получить плавные, прекрасные формы:

Можно вставлять объекты, которые деформируют сетку вокруг самих себя. В Ectogenesis я просчитал, как вода будет двигаться и преломляться вокруг объекта.

(Отмечу, что это было сложно)

Суммируя

Это почти всё, что я могу сказать о полях течения. Я думаю, что как и в любой технике, самое важное - понять их от А до Я, а затем расслабиться и делать все по-своему. Просто не используйте шум Перлина, и всё.