Доступ к среде (MAC, Media Access Control) в OpenUNB очень прост — случаен и асинхронен. Этот вид доступа еще называют асинхронная ALOHA. Даже WiFi может похвастаться более сложным вариантом MAC. За счет этого упрощения оконечные устройства OpenUNB могут сильно экономить в потребляемой энергии и стоимости оборудования. Но такой способ доступа к среде приводит к ошибкам при передаче, которые чаще происходят группами. Поэтому, хотя и не только поэтому, помехоустойчивому кодированию в OpenUNB уделено достаточно много внимания.

В настоящее время примером качественно спроектированных систем радиосвязи являются стандарты сотовой связи. Этот факт доказывается колоссальным прогрессом в способах передачи информации по радио, изменившим всю нашу жизнь. Детали реализации стандартов сотовой связи даже используются в профильных университетах, как условия задач. Создатели OpenUNB также не стали изобретать чего-то нового в смысле помехоустойчивого кодирования, а взяли пример со стандарта Интернета вещей от 3GPP — NB-IoT. Там при передаче в сторону базовой станции применяется полярное кодирование.

К слову, на Хабре есть отличные статьи по помехоустойчивому кодированию вообще и по кодированию LDPC в частности. Тем, кто путается в терминах и базовых понятиях, будет полезно их прочитать.

В настоящее время особую популярность набирает новый вид помехоустойчивых кодов, называемых полярными кодами. Как было доказано в [1], предложенные Ариканом полярные коды способны асимптотически достигать границы Шенона. Данное преимущество позволяет использовать полярные коды в современных телекоммуникационных системах мобильной связи. За довольно короткое время развития полярных кодов было предложено множество алгоритмов декодирования. Идея традиционного алгоритма декодирования [1] для полярных кодов заключается в последовательной оценке информационных бит. Таким образом, если на каком — то шаге декодирования происходит ошибка, то и оценка всех остальных бит тоже будет ошибочной. Такой алгоритм декодирования известен, как алгоритм последовательного исключения (ПИ). Одним из способов преодоления зависимости от оценок предшествующих бит является использование списочного алгоритма Тала-Варди.

В настоящей статье рассматривается списочный алгоритм Тала — Варди, предложенный в [2] для декодирования полярных кодов, который существенно уменьшает вероятность ошибки декодирование и позволяет реализовать декодирование почти по максимуму правдоподобия уже для небольшого размера списка (L = 16).

Основная идея, лежащая в основе алгоритмов кодирования и декодирования полярных кодов – поляризация канала. Поляризацией канала является операция преобразования канала связи в N независимых его копий, в которых вероятность ошибки при передаче данных стремится к 0, или к 1. Каналы с единичной вероятностью ошибки будем называть замороженными. Таким образом появляется возможность эффективного использования канала связи и передачу сообщений через множество каналов, обладающих низкой вероятностью ошибки. Полярные коды строятся на основе использования матрицы вида:

Матрица G называют ядром Арикана, а через m обозначают ее кронекеровскую степень. Формально алгоритм кодирования полярного кода состоит из двух основных этапов, а именно: формирования кодовой последовательности и умножения на матрицу Арикана. Под формированием кодового слова понимается вставка информационных бит в незамороженные позиции кодовой последовательности, и дальнейшее умножение этой последовательности на матрицу Арикана. Степень матрицы соотносится с длинной кодовой последовательности как N = 2^m.

Почитать о полярных кодах по-русски можно здесь, по-английски — здесь. Как введение в полярные коды рекомендуют это видео.

Для начала давайте проверим идею, что полярные коды действительно так хороши для нашего случая. Для этого сравним их с обычными конкурентами: БЧХ, Рида-Соломона, Голея. (Здесь следует заметить, что полярный код чувствителен к виду модуляции и что он особенно хорош именно при DBPSK.) Проведем имитационное моделирование в Matlab вероятности битовой ошибки в зависимости от отношения сигнал-шум на бит (ОСШб) указанных кодов с примерно одинаковыми скоростями. Результаты моделирования приведены на рисунке. По графикам видно, что даже в области малых значений ОСШб полярный код немного, но лидирует.

Выигрыш в 1 дБ или меньше может показаться мелочью, не достойной усилий. Но подумайте о радиоинженере, которому вы предложите уменьшить коэффициент шума уже вылизанного до предела приемника на 1 дБ, чтобы догнать конкурентов. Или подумайте о создателе сети IoT, которому нужно будет ставить базовые станции на 10 процентов чаще, чем конкурентам.

Следует отметить, что при более больших ОСШб разрыв полярного кода от конкурентов увеличивается. При ОСШб около 7.5 дБ вероятности ошибок уже отличаются на порядок, что будет приводить к значительно меньшим потерям пакетов.

Перейдем в практическую плоскость. Кодер полярного кода реализован в микроконтроллере, исходники здесь. В OpenUNB есть два варианта размера информационного блока: 64 и 96. Согласно алгоритму кодирования полярным кодом, необходимо сформировать промежуточную кодовую последовательность, которая будет содержать биты информационного блока в известных информационных позициях, а биты во всех замороженных позициях будут равны нулю. Код алгоритма представлен ниже:

int n_polar = _frozen_indicator.size();
std::vector<uint8_t> iwd_s(n_polar);
std::vector<int> inf_idx;
std::vector<uint8_t> u(n_polar);

for (int i = 0, j = 0; i < iwd_s.size(); i++) {
    if (_frozen_indicator[i] == 0) {
        iwd_s[i] = _iwd[j++];
        inf_idx.push_back(i + 1);
    }
    else {
        iwd_s[i] = 0;
    }
    u[i] = 0;
}

Результатом работы данного алгоритма является промежуточное кодовая последовательность размером 128 или 196 бит, соответственно. Далее для того, что бы умножить промежуточную кодовую последовательность на матрицу Арикана, необходимо дополнить промежуточную кодовую последовательность нуля до целой степени двойки. Умножение на матрицу Арикана осуществляется с помощью функции, приведенной ниже:

return solve_recursively_prep(inf_idx, u, iwd_s, n_polar);

Декодер реализован в приложении на Raspberry. Декодер получает от демодулятора DBSPK мягкие решения и реализует алгоритм декодирования Тала — Варди.

Основная идея списочного алгоритма декодирования состоит в том, чтобы обрабатывать сразу блок из не более чем L символов за одну итерацию алгоритма. То есть задача декодирования сводится к построению кодового дерева, где на каждой итерации вычисляется значение метрики пути, и строится не более чем L наиболее вероятных продолжений этого пути. В качестве примера приведем кодовое дерево (4,3), где 3 — число информационных бит.

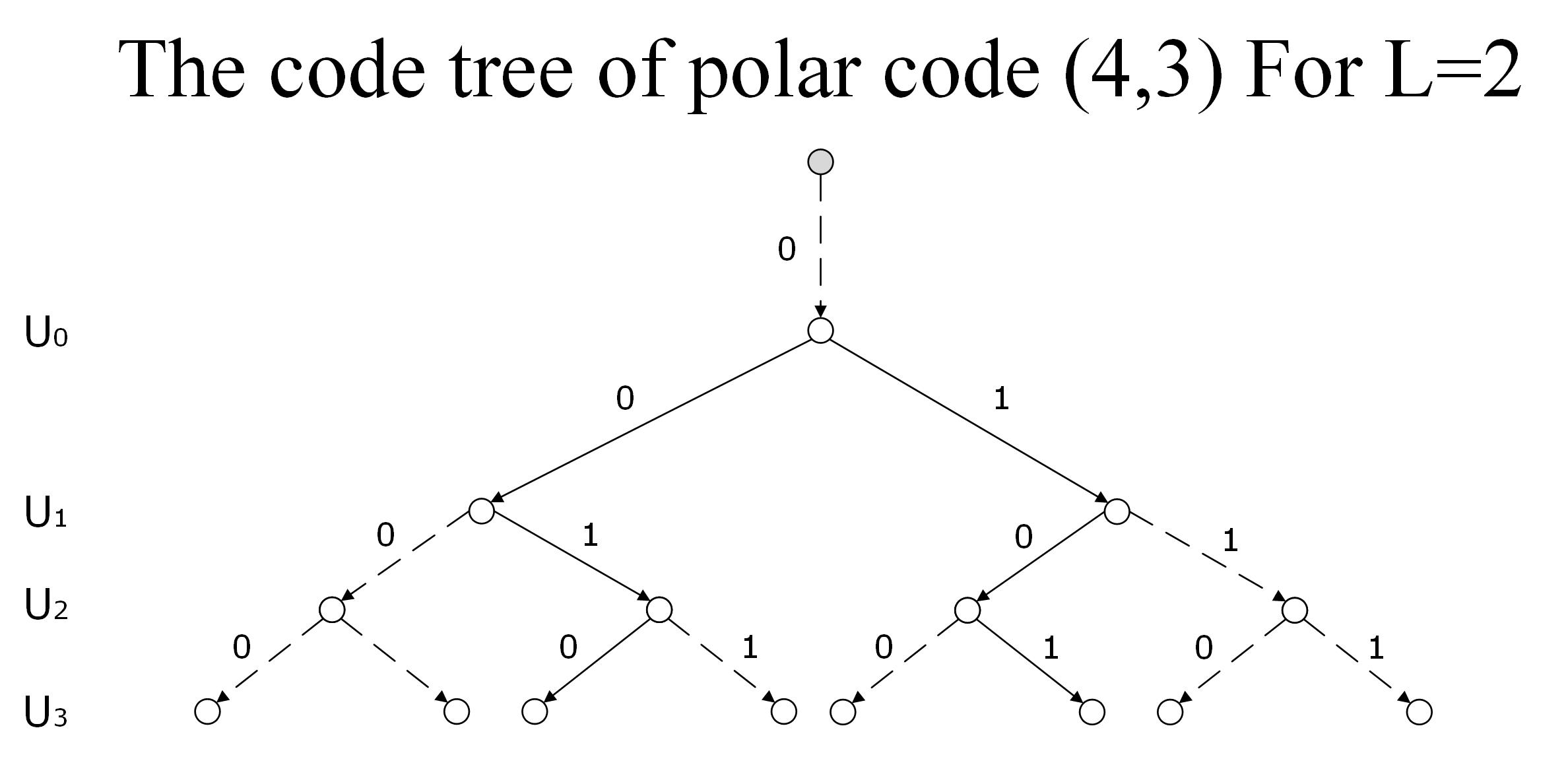
На рисунке, приведенном выше, сплошными линиями обозначены наиболее вероятные пути, причем количество этих путей определяется размером списка L.

По окончанию декодирования результатом будет являться список из L кодовых слов. Более того, было замечено, что правильное кодовое слово практически всегда присутствует в списке, формируемом этим алгоритмом. В связи с этим будем добавлять к данным, кодируемым полярным кодом, контрольную сумму CRC, значение которой можно использовать для выбора из списка решения задачи декодирования. В случае если несколько кодовых слов прошли проверку CRC, то решение принимается в пользу, того кодового слова, для которого значение модуля метрики будет минимальным.

Декодер:

std::vector<std::vector<float>> prob;
std::vector<std::vector<uint8_t>> dec = pcscl_prep(8, 16, llr, &prob, info_bit_pattern_96);
dec = polar_transform_noperm(dec);
dec = extract_with_filter(dec, crc_mask_96, num_of_nonzero_bits_96 - short_96);
std::vector<uint8_t> crc_err;
crc_err = crc_ok_array(0x327, dec);

Чтобы проверить соответствие реализации полярного кода идее, проводим натурное моделирование. Для этого создаем на столе такой стенд: подключаем RTL-SDR к Raspberry, включаем запись с эфира, запускаем передатчик и через аттенюатор записываем сигнал в файл. В софте читаем сигнал из файла, делаем измерение ОСШ и подмешивание к принимаемому сигналу шума. Далее запускаем процесс сбора статистики и уходим спать. По приходу мы имеем в распоряжении такой график:

График с точностью до погрешностей совпадает с графиком из модели в Matlab.

Попутно получаем график вероятности потери пакета в зависимости от ОСШ:

.

Последний график внушает оптимизм, зовет нас на местность, на улицу, пройтись с передатчиком, чтобы почувствовать мощь физического уровня OpenUNB.

P.S.

Хочется выразить благодарность нашему бессменному программисту deef137 и примкнувшему в нам специалисту по помехоустойчивому кодированию RadioTech34.

[1] Arikan E. Channel polarization: A method for constructing capacity achieving codes for symmetric binary-input memoryless channels // IEEE Transactions on Information Theory. –– 2009. ––July. –– Vol.55, no. 7. –– P. 3051–3073.
[2] Tal I., Vardy A. List decoding of polar codes // Proceedings of IEEE International Symposium on Information Theory. –– 2011. –– P. 1–5.