22.12.2020 04:17
zzeng 7 1900 Источник
image
Хвостом будем считать череду структур к западу от центральной кардиоиды вдоль по отрицательной части вещественной оси. В этой области таится целая бездна деталей. А в деталях, как известно, кроется дьявол … и его малютки.

Данная статья продолжает серию об устройстве множества Мандельброта.

Ранее мы изучали:

  1. свойства возведения в квадрат в комплексной плоскости,
  2. центральную кардиоиду.

Пришла пора продвинуться еще немного.

Большой довесок


Так будем называть круг множества Мандельброта с центром в точке (-1, i*0) и радиусом ?.

image
Фиг.1 большой довесок

Точка (-1, i*0) забавная, после возведения в квадрат превращается в (1, i*0), после добавления константы становится (0, i*0). На второй итерации возвращается в исходное положение.

Попробуем провернуть тот же трюк, что удался при исследовании центральной кардиоиды — посмотрим куда сходятся траектории, начинающиеся с приграничных точек.

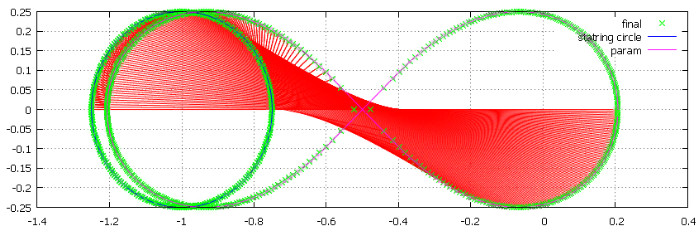
image
Фиг.2 финальные точки траекторий, стартующих с периметра “большого довеска”

starting circle — круг с центром в (-1, 0 i) и радиусом 0.2495. Честный радиус — 0.25, но точки с него сходятся крайне медленно.

final — по две точки на каждую стартовую. Обладают центральной симметрией относительно точки (-0.5, 0 i). Между углами в исходном круге и param разница в $\pi$.

Показана только половина соединяющих линий. Шаг — полтора градуса.

param — экспериментально полученная параметрическая кривая $R=? \sqrt{2 \cos{2\psi}} $, сдвинутая на (-0.5, 0 i).

Вообще, кривая param имеет четыре лепестка — два в вещественной области и два в мнимой. Это звучит странно т.к. мы уже находимся в комплексной плоскости.

Для начала проверим что две чисто вещественные точки переходят друг в друга.
Возьмём минимальную точку (-1?, 0 i)

  • для кривой param угол $\psi = 0$
  • константа C Из $(Z^2 + C)$ равна
    $C = -1 + ?cos(\pi+\psi) = -1 -? $
  • сама param в этой точке
    $inline$-? + ? \sqrt{2\cos{0}} = -? +? \sqrt{2}$inline$
  • квадрат param
    $? + ? - ? \sqrt{2}$
  • добавляем константу
    $inline$-? -? \sqrt{2} => -? + ? \sqrt {2 \cos(\pi)}$inline$
    получилось, угол 0 превратился в $\pi$,
    наоборот тоже работает

Теперь посмотрим на вещественные лепестки param.

  • разберем отрезок $\psi [0: \pi/4]$,
    в этой области $cos(2\psi)$ неотрицателен, как раз то что нужно
  • константа C Из $(Z^2 + C)$ равна
    $C = (-1 + ?\cos {\phi} , i ? \sin {\phi})$
  • угол окружности ($\phi$) и угол param ($\psi$) судя по приведенному графику связаны как $\psi = \pi - (\phi - \pi)/4$ или $\psi = (\pi - \phi)/4$
    $\phi = \pi - 4 \psi$
  • радиус param равен
    $R = ? \sqrt{2 \cos{2\psi}} =>\ ? \sqrt{2 \cos{((\pi-\phi)/2)}}$
    на интервале $\psi [0: \phi/4]$ R чисто вещественная
  • сама param в этой точке
    $(-? + R \cos{\psi}, i R \sin{\psi})$
  • квадрат param
    $Re = (-? + R \cos{\psi)}^2 - R(\sin{\psi})^2 \Longrightarrow $
    $? - R \cos{\psi} + R^2(\cos{\psi}^2- \sin{\psi}^2) \Longrightarrow $
    $? - R \cos{\psi} + R^2 \cos{2\psi} \Longrightarrow $
    $? - R \cos{\psi} + ? (\cos{2\psi})^2$

    $Im = 2 (-? + R \cos{\psi}) R \sin{\psi} \Longrightarrow $
    $ -R \sin{\psi} + R^2 \cos{\psi} \sin{\psi} \Longrightarrow $
    $ R \sin{(\pi + \psi)} + ? \cos{2 \psi} \cos{\psi} \sin{\psi} \Longrightarrow $
    $ R \sin{(\pi + \psi)} + ? \sin{4 \psi}$
  • добавляем константу C
    $inline$Re = -? + R \cos{(\pi + \psi)} -? + ? \cos{\phi} +? \cos{2 \psi}^2 \Longrightarrow $inline$
    $inline$ -? + R \cos{(\pi + \psi)} -? + ? \cos{\phi} +? \cos{4 \psi} + ? \Longrightarrow $inline$
    $ -? + R \cos{(\pi + \psi)} + ? \cos{(\pi - 4 \psi)} +? \cos{4 \psi} \Longrightarrow $
    $ -? + R \cos{(\pi + \psi)} $

    $Im = R \sin{(\pi + \psi)} + ? \sin{4 \psi} + ? \sin{\phi} \Longrightarrow $
    $ R \sin{(\pi + \psi)} $
  • в результате
    $(-? + R \cos{\psi}, i R \sin{\psi}) => (-? + R \cos{(\pi + \psi)}, i R \sin{(\pi + \psi)}) $
    что и требовалось.
  • в обратную сторону тоже работает

Теперь обратимся к мнимым лепесткам param.

В этой области $\cos{2\psi}$ отрицателен. Пусть $\Omega = ? \sqrt{|2 \cos{2\psi}|}$.

Тогда param:$ (i \Omega \cos{\psi} + i i \Omega \sin {\psi}) \Longrightarrow (-\Omega \sin{\psi} + i \Omega \cos{\psi})$.

Фактически, мнимые лепестки развернулись и легли поверх действительных.

Если бы не это, пришлось бы ломать голову, почему при $\phi [0:2\pi]$ мы попадаем на вещественные лепестки, а при $\phi [2\pi: 4\pi]$ нет.

Есть всё же в этом какая-то натяжка. Осталось ощущение очень мелкой возни и упущенной общей картины. Но по крайней мере теперь у нас в наличии есть оба элементарных блока из которых построено всё множество — круг и кардиоида. Осталось научиться смешивать их в нужных пропорциях.

Малые довески


Так станем называть более мелкие образования, нанизанные на отрицательную часть оси Re[C].
Минимальное значение, при котором последовательность, стартующая с оси Re[C] не расходится, это -2.

  1. -2 превращается в +4
  2. +4 при добавлении константы становится +2
  3. +2 превращается в +4
  4. ...

Всё что меньше -2 приводит к разгону последовательности.

А что происходит в интервале [-2:-1.25]?

Пройдёмся по этому отрезку и нарисуем предельные траектории, полученные с точек на нём. Поскольку мнимая часть на этом отрезке (для всех точек траектории) отсутствует, получается вполне наглядное представление — стартовая точка против финальных траекторных.

Финальными траекторными будем считать точки, полученные с помощью следующей эвристики.

  • первые 9000 итераций: делаем, но никак не учитываем.
  • следующие 1000 итераций: запоминаем точки траектории с точностью до 4 знаков после запятой
  • то, что накопили в результате и есть финальные точки, их может быть от 1 до 1000.

image
Фиг.3 Бифуркационная диаграмма для отрицательной реальной части константы.

Здесь для наглядности приведена часть множества Мандельброта в том же масштабе, соответствующая рассматриваемому отрезку.

Имеем дело с бифуркационной диаграммой для последовательности $Z_{n+1}=Z_n^2+C$.

  1. на интервале -0.75...0 последовательность сходится к одной точке, это соответствует центральной кардиоиде
  2. в точке -0.75 происходит бифуркация и последовательность выходит на предельный цикл из двух точек. Это область “большого довеска”. С центром в точке -1, для которой предельный цикл (-1 => 0 => -1).
  3. Далее идёт цепочка бифуркаций, при этом, как и положено, бифуркационный параметр при каждой следующем удвоении периода меняется всё меньше. Предел отношения последовательных изменений бифуркационного параметра называется постоянная Фейгенбаума и примерно равен 4.669. Этот предел универсален для всех рекуррентных последовательностей 2-й степени.
  4. Промежуток между бифуркациями на множестве Мандельброта соответствует кругу диаметра, равного этому промежутку.
  5. Однако, при соотношении диаметров 1 к 4.669, последовательность кругов очень быстро сходится, примерно при значении -1,40116 наступает предел. Назовём его “горизонт событий”.
  6. Но жизнь продолжается и за горизонтом событий.

    image
    Фиг.4 фрагмент бифуркационной ддиаграммы

    Каждый раз, когда мы видим на диаграмме “прогалину”, ей соответствует не просто окружность, а миниатюрная копия множества Мандельброта, со своей кардиоидой, большим и малыми довесками…

    image
    Фиг.5 фрагмент множества Мандельброта,
    центр (-1,4171..., 0), длина стороны 0.002668…

Как такое возможно?

Что объединяет все такие структуры?

Чем они отличаются от “довесков”?

Здесь наглядности, стоит привести бифуркационный “спектр” — зависимость длины предельного цикла от константы. Спектр получен с помощью эвристики и имеет значение только для оценки общей картины.

image
Фиг.6 бифуркационный спектр c шагом в 0.001

image
Фиг.7 спектр с разными шагами

Чем меньше шаг, тем больше выявляется циклов разной длины. Обратим внимание на характерные “лесенки” — удвоения периодов не только в изначальном каскаде бифуркаций, но и во всех “прогалинах/окнах периодичности”. Глядя на них невозможно не упомянуть теорему Шарковского

image
Фиг.8 порядок Шарковского

Оператор x image y означает, что если существует цикл длины x, обязан быть и цикл длины y. Нижняя строка соответствует начальному каскаду бифуркаций.

Лесенки у окон периодичности — столбцам вплоть до последней строки. С первой строкой, похоже, придётся повозиться.

Но вернёмся к бифуркационной диаграмме.

Вцелом картина неясна, поэтому зацепимся за что-нибудь, поддающееся осмыслению, потянем за эту ниточку и потихоньку распустим весь клубок.

Удачный кандидат быть такой ниточкой — самое большое окно за “горизонтом событий” — [-1.7684:-1.75] с длиной цикла 3. Взглянем поближе на все три непустых фрагмента этого окна.
image
Фиг.9 Центральная часть большого окна.

image
Фиг.10 Верхняя часть

image
Фиг.11 Нижняя часть

  • Как по команде, без перехода, в -1.75 хаос заканчивается и дальше идёт серия бифуркаций
  • Заканчивается всё собственным “горизонтом событий” этого окна.
  • Бифуркации во всех трёх ветках происходят синхронно.
  • Отрезок [-1.768:-1.75] соответствует местной кардиоиде, ниже идёт локальный “большой довесок” …
  • В -1.755 (примерно) центральная часть пересекает 0 и это соответствует 0 для основной кардиоиды множества Мандельброта.
  • В -1.755 нижняя часть равна -1.755

С этого и начнём.

  • Имеем цикл длины 3.
  • Одна из точек цикла — 0.
  • Из этого следует, что следующая точка цикла $0^2 + C => C$,
    в данном случае -1.755.
  • Последняя точка цикла => $1.755^2 -1.755 = 1.325$
  • Но что это за число -1.755, можно ли его получить аналитически?
  • Будем исходить из того, что в основной кардиоиде в точке ноль траектория так и оставалась в 0, никуда не мигрировала, здесь должно быть то же самое.
  • запишем переходы
    $0^2 + x => x$
    $x^2 + x => x_1$
    $x_1^2 + x => 0$
    следовательно
    $(x^2 + x)^2 + x = 0$
    $x^4 + 2x^3+ x^2 + x = 0$
  • вещественные корни уравнения — очевидный 0 и
    image
    или -1.7548776662...
  • Но что за полином такой? Нарисуем.

    image
    Фиг.12 Наложение полинома на бифуркационную диаграмму

    Внезапно оказывается, что это одна из тех странных кривых, которые живут потаённой жизнью внутри бифуркационной диаграммы.
  • Мы получили этот полином, когда три раза проитерировали исходное выражение
    $F_{n+1}= F_n^2 + x$ при $F_0= 0$
    Тогда
    $F_1= х$
    $F_2= x + x^2$
    $F_3= x + (x + x^2)^2$
    ...
  • А если продолжить и наложить на диаграмму несколько следующих итераций (мод).
    image
    Фиг.13 Несколько последовательных итераций/мод поверх диаграммы.
    Да, это они.

Однако, вернёмся к циклу длины 3, посмотрим на его фазовую диаграмму — зависимость текущего положения от предыдущего.

image
Фиг.14 Фазовая диаграмма траекторий циклов длины ~3, по X — предыдущее значение, по Y — текущее.

‘pp3center’ — проходит через 0
‘pp3start’ — максимальное значение диапазона, тоже длины 3,
‘pp3fin’ — за пределами диапазона цикл расщепился до длины 24.
Движение везде по часовой стрелке.

Лирическое отступление. Есть такое устойчивое выражение “period three implies chaos” (в порядке Шарковского всё начинается именно с трёх), то что мы наблюдаем проливает свет, почему именно 3.

В самом деле, из этих трёх два являются “обязательной программой” — 0 и начальное значение константы. Любое наблюдаемое окно периодичности содержит (центральную, основную, базовую?) траекторию, проходящую через 0. Почему, это отдельный вопрос, постараемся ответить на него позже. Но где есть 0, на траектории будет и начальная константа. А без этой парочки 3 превращается в 1, меньше которой уже и нет ничего. Т.е. есть циклы длины 1 и 2, которые мы видели и до “горизонта событий” в регулярной части бифуркационной диаграммы. Причем, цикл длины 2 сам является “обязательной программой”, а длины 1 — ещё и вырожденной оной.

А как насчет циклов большей длины? Судя по бифуркационной диаграмме с наложенными модами, если требуется найти цикл длины n, стоит поискать 0 для функции $F_n$. Это довольно просто проверить, для этого

  1. в gnuplot строится график $F_n$, например 
    set grid
set samples 10000
set xrange [-2:-1]
plot x+(x+(x+(x+(x+(x+(x+x**2)**2)**2)**2)**2)**2)**2
  2. на графике можно с приличной точностью найти один из вещественных корней, например, -1.9893204
  3. в любом онлайн — просмотре множества Мандельброта отмасштабироваться в нужную точку и voila

    image
    Фиг.15 возможный фрактал, соответствующий одному из корней моды $F_8$

    Надо еще кстати умудриться попасть в нужный фрактал, там ими всё буквально испещрено. Ведь мод бесчисленное количество и у каждой есть корни, число которых растёт по экспоненте с ростом номера моды. К счастью, размер фракталов при этом уменьшается.

И всё же, как это работает, почему когда мода пересекает 0, появляются фрактальные структуры?

  • до сих пор мы воспринимали траекторию как нечто цельное и уже полученное, на самом деле это итеративный процесс
  • т.е. сначала вычисляется $F_1$ затем $F_2$ …
  • Допустим, мы дошли до $F_n$ и случайно попали в стационарную точку, т.е. такую x, где $F_n(x) = x$,
    $F_n = x => $
    $x + F_{n-1}^2 = x => $
    $F_{n-1}^2 = 0 => $
    $F_{n-1} = 0. $
  • из этой точки невозможно выбраться, условно, мы уже никогда не попадём в $F_{n+1}$. Не теряя строгости можно считать, что сама $F_n$ является теперь элементарной рекуррентной функцией $\Phi_1 = F_n$, как если бы мы шагали сразу по n старых маленьких шагов.
  • стационарная точка может быть притягивающей и отталкивающей, отличаются они знаком второй производной
  • интуитивно понятно, что у притягивающей стационарной точки есть какая-то окрестность, в которой она притягивает траектории к себе как черная дыра пролетающие тела. Форма и размер этих окрестностей — предмет для отдельного/дальнейшего разговора, до сих пор мы встречали два варианта — кардиоиду как начало окна периодичности и круг в пределах регулярной части окна периодичности, вплоть до местного “горизонта событий”.
  • весь интервал [-2:0.25] заполнен бесконечным количеством окон периодичности самого разного размера, каждое из которых соответствует определенному корню какой-то моды.
  • эти окна вполне могут пересекаться, в этом случае окно моды с меньшим номером поглощает своего оппонента. Так как это происходит в точке 0, где вообще все моды имеют тривиальный корень.

Напоследок поглядим на фазовые диаграммы циклов длины больше 3.

Стартовые константы получены вышеописанным образом из gnuplot.

image
Фиг.16 Фазовая диаграмма траекторий циклов длины 4, в названии стартовая константа
‘pp4-1,3107’ получен двойной бифуркацией и находится до ‘горизонта событий’.
‘pp4-1.9408’ обход по часовой стрелке


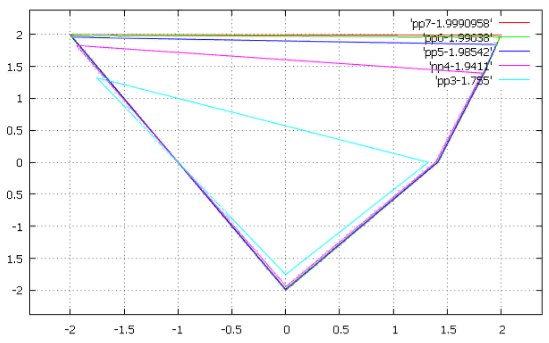
Фиг.17 Фазовая диаграмма траекторий циклов длины 5
Забавно, ‘pp5-1.98542’ получается из ‘pp4-1.9408’ изломом одной грани.


Фиг.18 Фазовая диаграмма траекторий циклов длины 6
‘pp6-1.77289’ получен расщеплением цикла длины 3.
‘pp6-1.99638’ получен дальнейшим изломом грани в ‘pp5-1.99638’
‘pp6-1.75488’ порождает цикл длины 3 т.к. попадает в окно с периодичностью 3, которое имеет приоритет.

Далее мы не будем смотреть на все имеющиеся циклы, с ростом периода число корней моды растёт экспоненциально, да и степени в полиномах возникают такие, что как-то становится тревожно за точность gnuplot. Просто поглядим на субъективно интересное.


Фиг.19 само-непересекающиеся циклы длины 3...7

Эти циклы разного размера, но имеют близкую родственную связь. Заключается она в том, что всё это циклы с минимальным корнем соответствующей моды.

Аналогичный цикл длины больше 7 отловить не удалось из-за нарастающей потери точности в вычислениях.


Фиг.20 Еще одна серия траекторий с ростом длины циклов по единице.
Это, кстати, вторые снизу минимальные корни.
По-видимому, это (+1) вполне популярная история. Возможно, стоит продолжить.


Фиг.21 Третьи снизу корни мод.

В принципе логика понятна.


Фиг.22 Фазовая диаграмма траектории длины 11.

Здесь хорошо видно, как нарастает число “зубьев”, а также то, что точки фазовой диаграммы находятся на параболе, что логично, учитывая их происхождение.

Однако, и это еще не всё. Встречаются и вот такие жемчужины:


Фиг.23 цикл длины 9 — утроение цикла.

До сих пор мы встречали только удвоение циклов, например, “pp6-1.77289” из “pp3-1.755”.


Фиг.24 удвоение и утроение цикла 3.

Цикл 3 при -1.755.
Цикл 6 при -1.77289
Цикл 9 при -1.7859
Утроение (-1.7859) находится за локальным “горизонтом событий”.
И, по видимому, соответствует “циклу 3*3 за горизонтом событий цикла 3”.
Если гипотеза верна, между [-1.7859:-1.7783] мы найдём и цикл 3*6 и 3*5 … (если точности хватит)


Фиг.25 Бифуркационный “спектр” в интересующем нас интервале.

Невозможно не отметить, насколько этот кусочек спектра похож на полный спектр, приведенный выше (Фиг.7). Что еще раз указывает на фрактальную природу происходящего.


Фиг.26 Расщепление цикла 3 на 4, 5, 6 частей

И до кучи, вот так выглядит попадание мимо окна периодичности (если вообще можно попасть мимо окна периодичности), либо очень большой цикл, что в общем то одно и то же.


Фиг.27 псевдо-хаотическое поведение, длинный цикл.

Подводя итоги, нельзя не отметить что данная статья поднимает больше вопросов, чем даёт ответов.

Чем всё же определяется форма и размер больших и малых довесков?

Как связаны между собой моды?

Неужели мы забыли, что у полиномов есть не только вещественные корни?

Не торчат ли здесь уши сферических функций?

…

Что же, будет чем заняться дальше.