Идея сделать цифровые логические микросхемы с изменяемой структурой была всегда. Почему? Достаточно посмотреть на толстенный каталог чипов серии TTL 74xx (или советской К155), чтобы такая идея самозародилась. В СССР почти у каждого инженера и радиолюбителя был справочник В.Л. Шило «Популярные цифровые микросхемы», который вышел каким-то невероятным тиражом. Но всё равно, хотелось иметь некий «универсальный кристалл», из которого можно сделать все остальные микросхемы (ну хорошо, не все, но многие).

Конечно же, полупроводниковая промышленность тоже была не прочь удовлетворить такой спрос. Поэтому, начиная с конца 1960-х, на рынке каждый год появлялось огромное количество подобных устройств из класса PLD (Programmable Logical Device), самых разнообразных архитектур. Это было интереснейшее время! На рынке постоянно появлялось что-нибудь новенькое. Здесь были и различные ULA и БМК и EPROM-устройства на базе пережигаемых перемычек (82Sxxx) и PLA, у которых программировались оба слоя: «И» и «ИЛИ» (привет нашим К556РТ1 и К556РТ2) и т.д. Обзор этих ретро-технологий – тема для отдельной статьи. Мы же сделаем лишь обзор того, что «выстрелило» и стало мэйнстримом.

Сразу хочется попросить извинения у опытных электронщиков и разработчиков FPGA. Эта статья нисколько не имеет цели вторгнуться на их территорию, а только дает исторический обзор «как это было».

А в конце мы попробуем соединить теорию с какой-то осмысленной практикой, поглядеть, как это применяется в реальной жизни. Светодиод, например, зажечь или там даже семисегментный индикатор…

MMI

Так вот, в далекие 1970-е годы компания-производитель ПЗУ Monolithic Memories Inc. (MMI) выпустила на рынок очередное семейство программируемых чипов. Семейство ВНЕЗАПНО оказалось настолько удачным, что в 1978 году MMI зарегистрировала торговую марку PAL® (Programmable Array Logic) и стала лицензировать технологию таким гигантам, как Texas Instruments (серия TIBPAL), National Semiconductor, Philips (PLUS), AMD (AMPAL) и другим.


Даже в СССР не отставали и выпустили клоны, серию К1556.


В чем же секрет? Спроектированное инженерами и для инженеров семейство MMI PAL представляло собой практически чистое воплощение идеи ДНФ (Дизъюнктивная Нормальная Форма).

Здесь надо сделать логическое отступление и взглянуть, что же это такое, ДНФ и откуда оно взялось.

Матлогика

Дискретная математика и мат-логика вообще – наука большая и развесистая. Мы не будем залезать в дебри и высокую теорию, а лишь рассмотрим узкий срез — работу с логическими (булевыми или же переключательными) функциями и соответствующими комбинационными схемами.

Лирическое отступление: есть огромное искушение ничего не писать, а просто посоветовать взять и прочитать недавно переведенный учебник Харрис&Харрис «Цифровая схемотехника и архитектура компьютера», а конкретно главу 2 «Проектирование комбинационной логики». Это отличная книга! Там даже есть параграф про PAL (п.5.6 «Матрицы логических элементов»), но такое ощущение, что его безжалостно сократили в очередной редакции.

А для тех, кто захотел канонично, «от печки», разобраться в предмете поглубже (бывает!) можно порекомендовать книги 60-х годов по проектированию ЭВМ. Например, книгу “Синтез цифровых автоматов” В.М. Глушкова (тот самый, который ОГАС!) (М. Государственное издательство физико-математической литературы, 1962г). Книга настолько олдовая, что фамилия Карно записывается как Карнаут. Или можно предложить книгу ”Синтез схем электронных цифровых машин” (Е.Н.Вавилов, Г.П.Портной М. ”Советское радио” 1963).

В современных отечественных учебниках, чем дальше, тем больше этот раздел ужимается.
Например учебник Угрюмов Е.П. «Цифровая схемотехника» издания 2007 года еще содержал главу про PAL, а издания 2010 — уже нет. В настоящее время данная наука почти полностью перекочевала в пыльные бумажные методички кафедр по специальности 230101. Вдобавок, попытка дать студентам этот материал наталкивается на стойкое сопротивление: разговоры про «основы» воспринимаются учащимися как «too old» то есть как совершенно ненужный, устаревший хлам. Даже тут, на Хабре есть несколько статей на данную тему, и комментарии наполнены стонами ”Да-да! Нас тоже зачем-то насиловали этим весь первый курс!”.

Так вот, автор сбрасывает себя обязанность писать про пресловутые ”основы”. Предполагается, что читатель, который заглянул на огонек, всё-таки понимает, что такое булева алгебра, что такое И, ИЛИ, НЕ, знает теорему де Моргана и умеет читать схемы на логических элементах.

ПРИМЕЧАНИЕ: Мне тут подсказывают, что в современном курсе цифровой электроники эта дисциплина (Дискретная математика) и Цифровая схемотехника чаще всего разделены на два предмета и учебники у них — разные. А Харрис&Харрис в попытке впихнуть все в одну книгу породил монстра на 1600 страниц. Ну OK.

Ах да, ДНФ. В старых книжках говорится (объясняется — почему), что при достаточно сложном логическом выражении его лучше всего представить (и это можно сделать для любого выражения!) в виде дизъюнктивной нормальной формы (sum of product, SOP). Несмотря на страшное название, это очень просто. Возьмем логическую функцию Y от трех переменных, A, B, C. Пусть она принимает значение «истина» тогда и только тогда, когда все три входные переменные равны нулю или же все они равны единице. В ДНФ это запишется крайне просто:



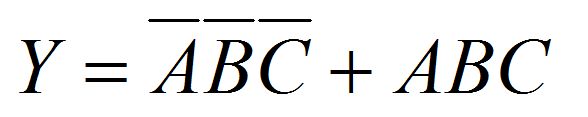
Это так называемая алгебраическая форма. Операция «ИЛИ» тут записывается как «+», а операция «И» — как умножение и, как в обычной алгебре, опускается. Так получилось, что существует множество форматов записи (синтаксисов) булевых выражений. Вот в другой записи:



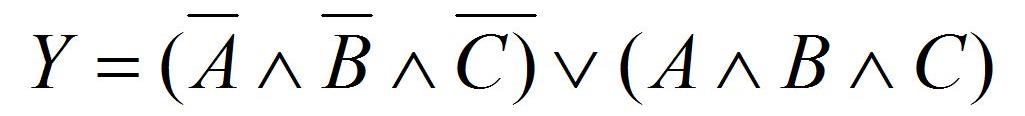
Си-шное выражение для bool переменных:



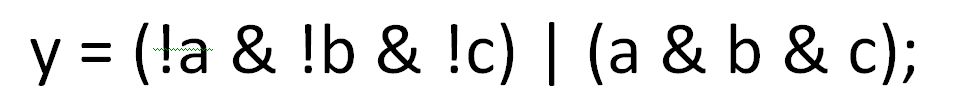
Или даже так (синтаксис PALASM):



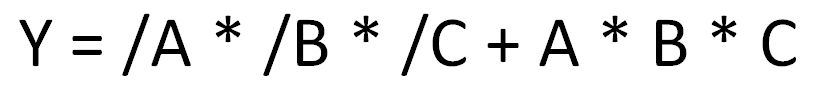
То есть ДНФ (в алгебраической форме) выглядит как цепочка сложений т.е. многочлен (логическое ИЛИ) из произведений (логическое И) входных переменных (sum of product), причем только тех комбинаций, для которых должна получаться «истина». Интуитивно это довольно понятно: Истина, когда это И это, ИЛИ же когда то И то. Как выше упоминалось, в форме ДНФ можно представить любое логическое выражение (и помним, что мы не углубляемся в СДНФ, КНФ, СКНФ, критерий Поста и т.д.).

Оптимизация, оптимизация

Другая, ныне забытая дисциплина при изучении данной науки – это методы оптимизации логических выражений. Современному разработчику практически не надо заботиться об оптимизации, за него все сделает «умный» компилятор. Да, напрямую к PAL оптимизация выражений отношения не имеет, но чтобы понять дух эпохи, давайте посмотрим.

На самом деле, методов оптимизации существует довольно много. Самый простой — алгебраический, когда преобразуется выражение по законам булевой алгебры (она слегка похожа на обычную, но чуть другая). Можно еще упомянуть теорему Квайна (и метод Квайна – Мак-Класки), метод получения тупиковых форм, метод испытания членов, метод импликантных матриц и т.д. Отдельно где-то парит полином Жегалкина на базисе Исключающее-ИЛИ. Методов много. Самыми удобными оказались диаграммы Вейча или, в усовершенствованном виде — карты Карно.

Для изучения механизма работы карты Карно можно, опять же, отправить к учебнику Харрис&Харрис глава 2.7. Но очень уж изящное решение! Кроме того, карты Карно иногда спрашивают на собеседованиях. Карты Карно предназначены для визуального безкомпьютерного упрощения выражений с количеством переменных до 6.

Давайте посмотрим на типичную карту Карно, например на 4 переменных:


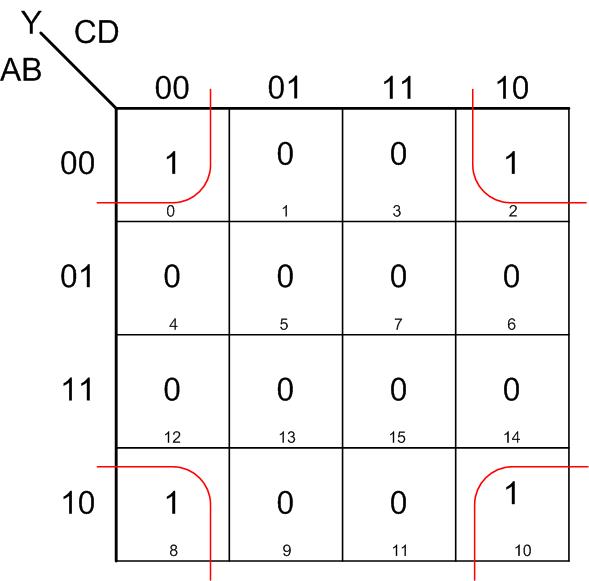
Самое важное (и в чем состоит суть изобретения Мориса Карно) – это то, что соседние клеточки по вертикали и горизонтали отличаются значением ровно одной переменной. А если в соседних ячейках стоят «1» то эту переменную можно исключить. Причем «края» карты Карно подразумеваются «склеенными». Так что наша функция ужимается до



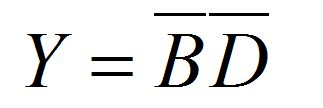
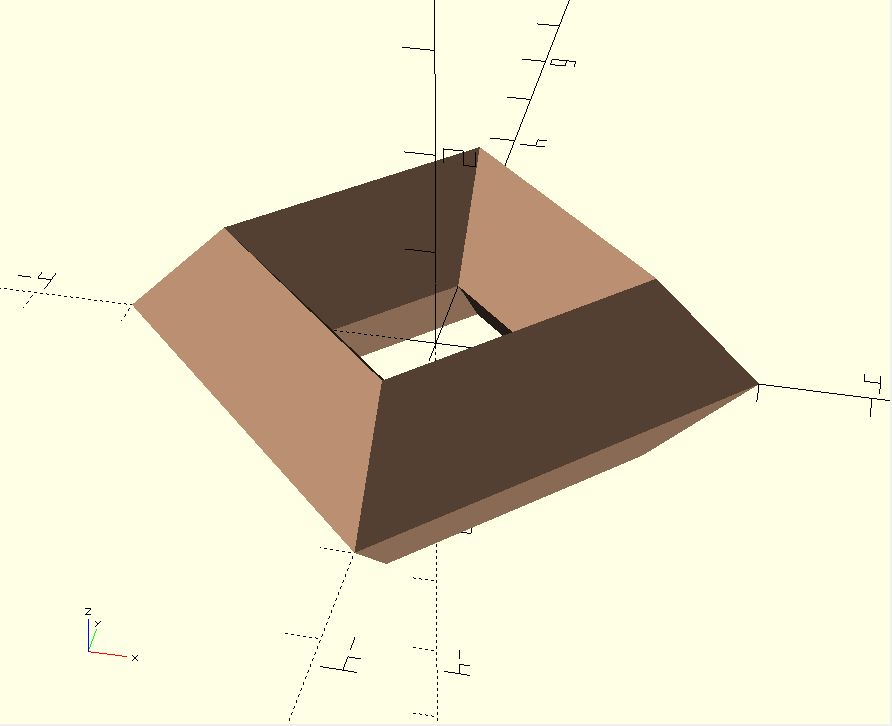
Если попытаться изобразить в 3D карту Карно для 4-х переменных, ее можно будет представить как развертку такого «угловатого тора», имеющего 16 граней (нарисовано в OpenSCAD ).

Возвращаясь к PAL

Обогатившись такими знаниями, давайте вернемся к нашим PAL-кам и посмотрим на их внутреннее устройство. И опять же, хорошим подспорьем тут будет учебник Харрис&Харрис «Цифровая схемотехника и архитектура компьютера», а конкретно параграф про PAL (п.5.6 «Матрицы логических элементов»).

При разработке PAL применяется своеобразная графическая запись, первоначально, видимо, предназначенная для ручного кодирования (до появления PALASM).

Давайте возьмем одну ячейку PAL, самого классического PAL16L8:


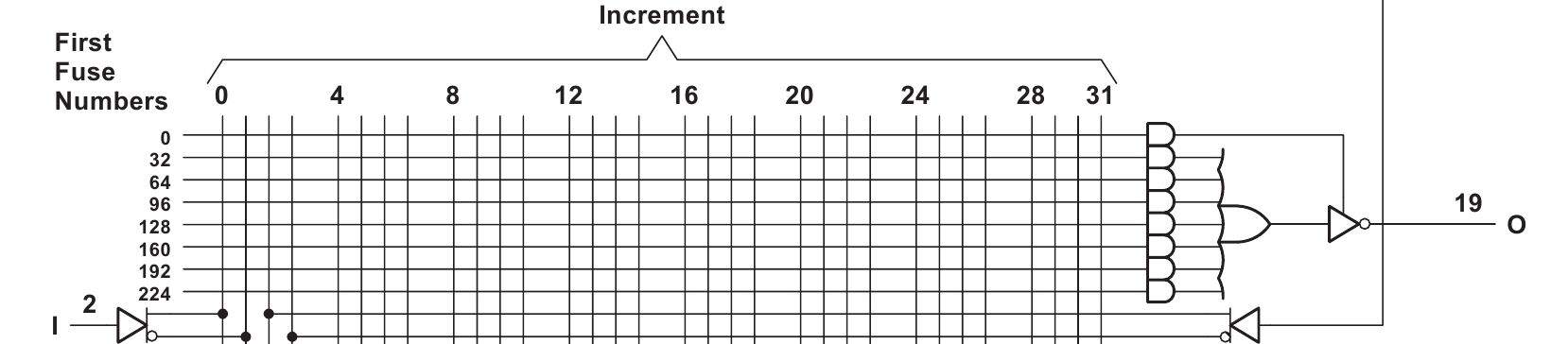
Итак, сверху вниз идут колонки – входные переменные. Из них: 10 шт. – это самые настоящие входы, то есть «ножки» микросхемы, а 6 шт. – это «возвраты» внутри чипа, что позволяет создавать более сложные многоступенчатые выражения. Понятно, что каждая из этих 16 переменных существует в прямой и инверсной форме, итого мы видим 16*2=32 колонки. Слева мы видим ввод одной переменной в матрицу, в прямом и инверсном виде (вывод 2).

Все эти «вертикальные» переменные одновременно поступают на элементы «И», которые могут использовать некоторые их них (а могут не использовать). Схема примерно такая (тут нарисованы две входные переменные и два элемента «И»):


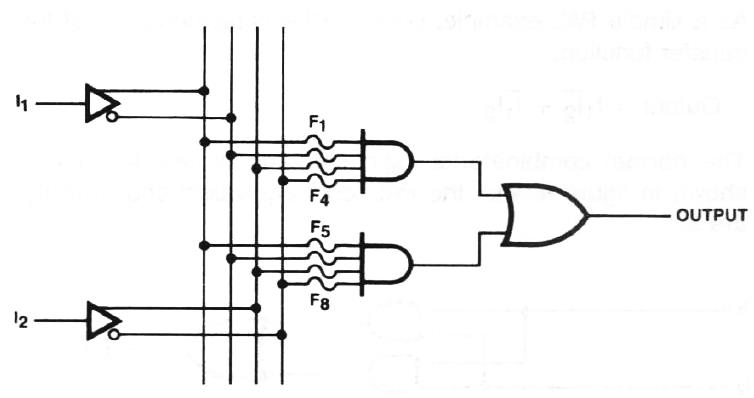
Мы видим «плавкие перемычки» (fuse, F1..F4 и F5..F8), которые задают, какие переменные подключены к «И». Именно эти fuse и программируются и задают логическую функцию PAL. Картинка получается довольно громоздкая, поэтому применяют такую сокращенную графическую запись (крестики – это подключенные входы):


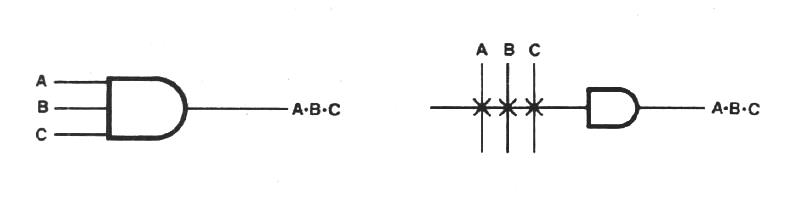
Вернемся к схеме ячейки PAL:


Как видите, в каждой строке (горизонтали) можно собрать функцию «И» из 16 (32, учитывая инверсию) возможных входов (переменных). То есть такая вот строка – это на самом деле 32-входовый элемент «И» (программируемый). Чуть позже мы посмотрим, как эти соединения выглядят в прошивке.

Далее по схеме мы видим, что в PAL16L8 имеется 7 штук таких «И-шек», объединенных по «ИЛИ». Структура у «ИЛИ» у PAL фиксированная (в отличии от PLA и других архитектур) и не программируется. Кстати, обратите внимание, можно использовать меньшее количество «ИЛИ» (просто не задавая функций у «И» в ячейке), а вот больше – нельзя!

Как несложно заметить, такая конструкция и является физической реализацией ДНФ или SOP (Sum Of Product – то есть сумма произведений). Бинго!

Такие устройства стали называться SPLD (Simple PLD) в противовес CPLD (Complex PLD) и FPGA. Про CPLD кстати, имеется отдельная статья.

Такая простая и элегантная конструкция быстро стала чрезвычайно популярной и стала быстро вытеснять остальные семейства. Вот почему такие гранды, как AMD, Philips, National Semiconductor лицензировали ее.

Популярность PAL-ок пришлась на середину 80-х и начало 90-х. Многие производители чипов, прямо в Datasheet-ах публиковали листинги на PALASM для подключения своих микросхем к другим чипам и к разнообразным микропроцессорным шинам. Некоторые платы начала 90-х представляли собой «россыпи» PAL-ок, на которых были реализованы сложнейшие схемы. Это позволяло быстро выйти на рынок, до начала производства заказных микросхем LSI. (Погуглите, ну скажем, картинки материнской платы EISA i486 Everex Step Mega Cube или Intel iSBC 386. Все узкие микросхемы с бумажками – это PAL ).

Сейчас эту нишу занимают CPLD и FPGA.

Компания MMI выпускала книжки, содержащие массу примеров применения своих микросхем, которые сопровождались забавными рисунками (извините, утащил).


Или даже так, ужас-ужас (Текст: В этой конструкции одна PAL16R8 заменяет 15 TTL микросхем малой и средней степени интеграции ):


Семейство PAL было довольно обширное. Существовали разновидности на разное количество ячеек и входов. Были разновидности с триггерами, что позволяло делать на них синхронные схемы и даже маленькие конечные автоматы (например PAL16R8). Существовали универсальные (Versatile) разновидности, в которых можно выбирать комбинаторную логику или триггера (PAL16V8). Существовали чуть более крупные PAL-ки в 24-выводном корпусе, типа PAL22V10. Микросхемы могли быть упакованы в различные корпуса и могли быть разной «скорости», от -5 до -25 наносекунд. Наконец, существовали низкопотребляющие варианты и варианты в CMOS исполнении (например Texas Instrument TICPAL или Cypress Semiconductor PALC).

PALASM

Невероятный успех микросхемам PAL фирмы MMI принёс еще один компонент, без которого покорение рынка было бы немыслимо. Это — утилита PALASM. С ее помощью создание прошивки для PAL стало делом настолько легким и простым, что любой инженер с нормальной подготовкой, понимал идею практически сразу. В PALASM вводится названия пинов и логические выражения в человеческой алгебраической форме (которые обычно выглядят как ДНФ), после чего PALASM выдает файл прошивки для программатора (JEDEC). Грубо говоря, компания MMI сделала тот шаг, который когда-то в 1950-е прошли обычные компьютеры, при переходе от ручного выписывания двоичных кодов к более понятной записи выражений машинного языка (ассемблера). А сам PALASM первых версий, в свою очередь, был написан на языке FORTRAN IV и распространялся в исходных текстах, что позволяло запускать его на любой тогдашней машине, где был компилятор, вплоть до ранних персоналок под CP/M и DOS. Да, да, когда-то FORTRAN был общим системным языком для переноса программ…

Позже вышел PALASM2, синтаксис немного изменился, оброс разнообразными возможностями, появилось некоторое подобие макросов, оптимизатор, поддержка конечных автоматов и даже симулятор. Компания MMI тоже претерпела изменения, ее активы были поглощены AMD, потом выделены в отдельную компанию Vantis, которую позже купила Lattice Semiconductor. Сам входной язык PALASM послужил прообразом множества подобных и более продвинутых языков, его следы есть в ABEL, CUPL и в VHDL (а вообще-то он сам вырос из FORTRAN-а ).

Наиболее развитый PALASM – это версия PALASM4 v1.5a от AMD 1992 года. Понятно, что такая ретро-программа требует для запуска ретро-DOS. Но к счастью, этот вопрос давно решен. Тут нам поможет прекрасная утилита DOSBOX, позволяющая запускать DOS-программы даже на современном Windows 10 64-бит. Хотя DOSBOX вообще-то, предназначен для запуска ретро-игр, но и не-игровые DOS-утилиты неплохо в нем живут и PALASM — не исключение. Компания AMD сделала широкий жест и отпустила PALASM в Public Domain, так что пользоваться им можно совершенно легально.

Тут можно найти инструкцию, как поставить PALASM на DOSBOX и также скачать саму программу. Конфигурационный файл DOSBOX хранится в профиле пользователя
C:\Users\%USERNAME\AppData\Local\DOSBox\ dosbox-0.74.conf
Лучше дополнить секцию [autoexec]:

...
...
[autoexec]
# Lines in this section will be run at startup.
# You can put your MOUNT lines here.
@echo off
mount c c:\DOSBOX
set PALASM=C:\PALASM
set PATH=%PATH%;C:\PALASM
C:

Из под Linux тоже можно запустить PALASM например с помощью того же DOSBOX или похожего DOSEMU.

Из PAL в GAL

При всём своём удобстве PAL-ы имели и некоторые проблемы. Одна из таких проблем состоит в том, что PAL – это однократно программируемое устройство (OTP) с плавкими титано-вольфрамовыми перемычками (Ti-W fuse). При появлении исправлений и замене прошивки приходилось старую микросхему просто выкидывать. Так что многие производители стали предлагать ”стираемые” PAL-ки. История тут длинная, можно, например, вспомнить УФ-стираемые чипы с «окошечком», или тот факт, что очень хотелось сохранить совместимость с парком программаторов и алгоритмами прошивки оригинальных PAL (серии PALCE и PEEL от International CMOS Technology (ICT) Corporation) и т.д.

Наконец фирма Lattice Semiconductor в 1985 г. выпустила семейство GAL, которое можно считать своеобразной вершиной PAL-строения. Подобно исходным MMI PAL-ам c буковкой V ( Versatile) (например PAL16V8) чипы GAL (соответственно название будет GAL16V8) могут принимать прошивки ВСЕХ (ну почти) моделей PAL, а вдобавок чип GAL — электрически стираемый и многократно прошиваемый. Устройства GAL практически вытеснили все остальные SPLD, за исключением, пожалуй Atmel (нынче Microchip) серии ATF (аналогичный чип у них будет называться ATF16V8).


Для переноса JEDEC файлов (прошивок) старых PAL фирма Lattice Semiconductor выпустила утилиту PALTOGAL (тоже бесплатную и тоже под DOS).

ПРМЕЧАНИЕ: Фирма Lattice Semicronductor рекомендует использовать для разработки ABEL (пакет ispLEVER), а фирма Atmel – CUPL (WinCUPL или ProChip Designer). National Semiconductor предлагала свой Opal JR. Но мы в ретро-целях останемся верны PALASM.

ПРИМЕЧАНИЕ2: (для совсем нердов) У GAL все же есть некоторые мелкие отличия, связанные с тем, что MMI PAL – это ТТЛШ микросхема, а GAL – CMOS.

И конечно же, для прошивки микросхем GAL (и ATF) потребуется специальный программатор. Существуют и PAL-ы, прошиваемые по JTAG, но это редкость (Lattice ispGAL). Хотя программатор для GAL можно сделать самостоятельно (ищется по именам GALBLAST и ATFBLAST), всё же лучше приобрести готовый. Например, TL866 (известный еще как Minipro), которыми забит Aliexpress:


Сами чипы GAL или ATF можно приобрести на том же Aliexpress. Цена за десяток может доходить до 5$ и менее. Не стоит ожидать чудес, чипы будут б/у (помним, что их можно и нужно(!) стереть) и могут иметь следы пайки и маркировку краской или лазером от погибших неведомых устройств, откуда их вытащили трудолюбивые китайцы. Lattice GAL сняты с производства в 2011, но запасов из старой техники хватит еще на пару десятков лет. ATF еще выпускаются.

7-SEG LED

Если помните, в начале статьи мы собирались зажечь светодиод. А точнее — не один, а целых семь! Да- да, речь пойдет о 7-сегментном индикаторе, а точнее – о реализации банального дешифратора HEX-to-7SEG.


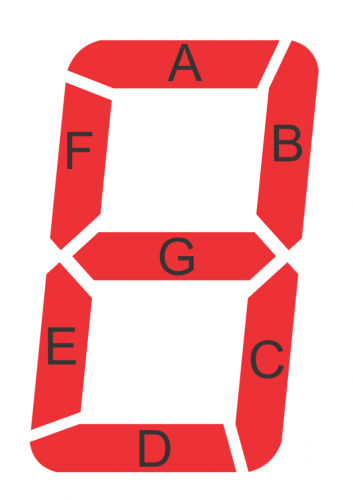
Почему-то так сложилось, что готовых микросхем с такой функцией не так уж и много. Есть десятичные BCD дешифраторы (т.е. без шестнадцатеричных символов ABCDEF), например 7446/7447/7448/7449 и 74246/74247/74248/74249). Полных HEX дешифраторов не так много — например Motorola MC14495 Hexadecimal-to-Seven Segment Driver или Fairchild DM9368.

Но цены на PAL (GAL) упали настолько, что сделать дешифратор на SPLD дешевле и быстрее! Вот и давайте для практики его и сделаем, включая шестнадцатеричные цифры ABCDEF (Нет, ЕГГОГ мы декодировать не будем ). Отличное приложение наших олдскульных знаний по матлогике и старым программируемым микросхемам.


Построение такого дешифратора является каноническим примером комбинационной логики и типовой лабораторной работой. В учебнике Харрис&Харрис «Цифровая схемотехника и архитектура компьютера» пункт 2.7.2 «Логическая минимизация на картах Карно» содержит пример 2.10 построения такого дешифратора, но только BCD.

На Википедии есть статья, в которой даже приведена нужная нам таблица перекодировки для полного HEX.

Вот эта же самая таблица, только здесь зажигание нужного светодиода отмечено красными клеточками. Как видите, никакой регулярности, только таблица, только хардкор!


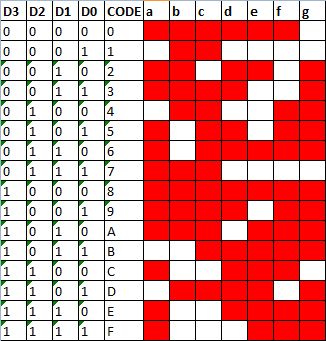
Давайте для примера рассмотрим сегмент D (нижний). Как мы видим, он загорается 11 раз из 16 возможных входных комбинаций (вертикаль «d»). Если выписать ДНФ, то формула будет такой:



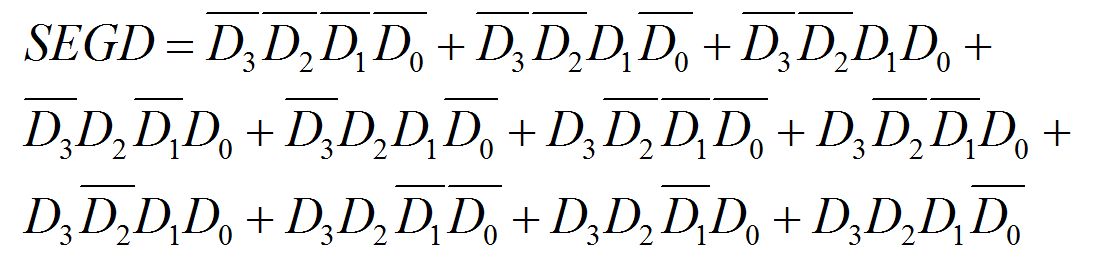
Но здесь есть проблема! Как мы писали выше, матрица обычных PAL (например в PAL16L8) имеет только 7 «ИЛИ» (сложений), а у нас — 11. Надо или применять более сложный чип или выражение придется оптимизировать.

ПРИМЕЧАНИЕ: В PALASM4 есть встроенный оптимизатор. Вероятно, он смог бы упростить это выражение, только надо эту оптимизацию включить. Но для сохранения ретро-духа пройдем этот этап вручную.

Давайте оптимизируем это выражение по карте Карно. Можно сделать это вручную и получить удовольствие, а можно воспользоваться сайтами, где на JavaScript реализованы эти алгоритмы, например:

• http://www.32x8.com/index.html
• https://charlie-coleman.com/experiments/kmap/

На втором сайте в качестве переменных можно вводить: D3,D2,D1,D0. Далее, вводятся номера единичных минитермов (фактически, это входные числа, для которых загорается сегмент D), у нас это 0,2,3,5,6,8,9,11,12,13,14 (0,2,3,5,6,8,9,B,C,D,E) – проверяем по красным клеточкам.


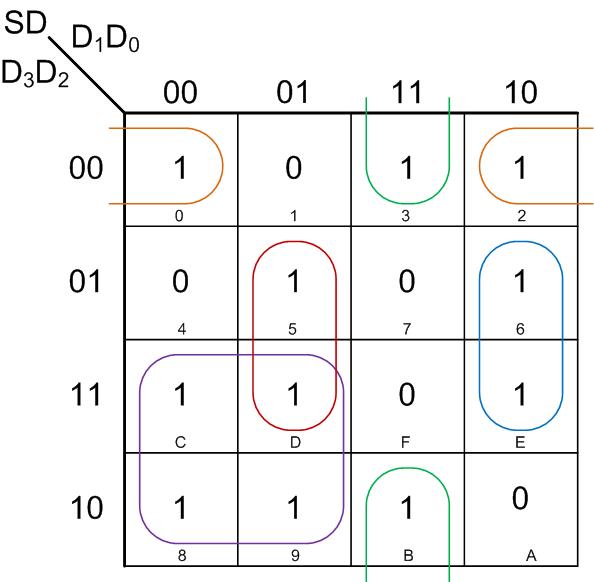
Как видите, наше выражение для сегмента D превращается в короткое:


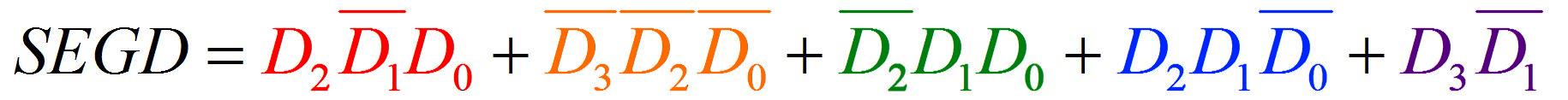
Тут всего 5 штук «ИЛИ» вместо 11 так что выражение влезает в ячейку PAL. Проделаем это для всех сегментов.


Откомпилируем файл .PDS в файл .JED с помощью PALASM:


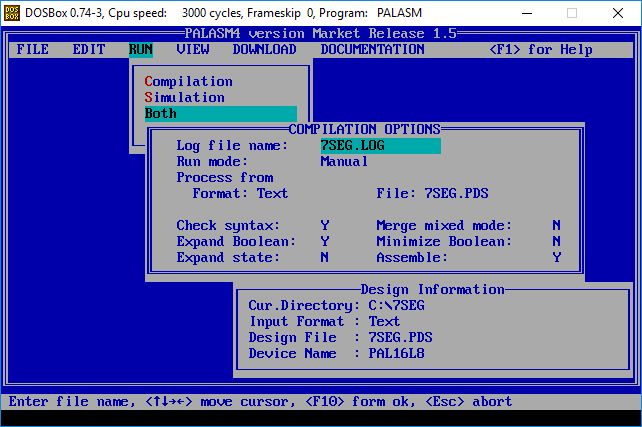
Очень интересно, как PALASM разложил наши выражения на плавкие перемычки. Для этого можно заглянут в файл Fuse plot (рисунок перемычек).


Этот файл лучше рассматривать одновременно с документацией на PAL16L8. Ее можно найти, например, на сайте Texas Istruments: pal16r8am.pdf страница 5.

Сегмент D у нас выведен на 16-й вывод микросхемы. Если мы посмотрим схему PAL, то за него отвечают перемычки, начиная с номера 768. Как несложно догадаться 768 / 32 = 24 – это 24-я строка. Сама она отвечает за управление выходом и поэтому пустая. Логические выражения начинаются с перемычки 800, то есть строки 25. Если посмотреть на схему, то в 25-й строке собираются по «И»: прямой вход D0 (вывод микросхемы 2), инверсия D1 (вывод 3) и прямой вход D2 (пин 4). Это в точности соответствует первому минитерму в формуле для сегмента D! Остальные минитермы из выражения также транслируются в перемычки и в конце объединяются по «ИЛИ». Так что PALASM, не мудрствуя лукаво, просто переводит наши ДНФ-выражения в прошивку один в один.

Именно таким способом проектировали прошивки до появления PALASM, в самой старой документации MMI как раз описан этот способ. Надо отметить, что другие семейства, например PLA, не получили вообще или получили утилиты класса PALASM довольно поздно (например ICT PEEL Array PLACE) и не стали такими популярными.

Для программирования GAL полученный файл 7SEG.JED отконвертируем утилитой PALTOGAL:

PALTOGAL –C2 –R 7SEG.JED 7SEG_GAL.JED

При подключении индикатора к FPGA (на VHDL и Verilog) или к микроконтроллеру логические функции раскладывать нет необходимости и просто используют таблицу. Можно погуглить или посмотреть на Youtube, поиск «Семисегментный индикатор».

Практика

Давайте соберем модель декодера семисегментного индикатора (и сдадим курсовик, ха-ха). В качестве генератора импульсов применим обычную микросхемку NE555 (К1006ВИ1). Для наблюдения нам нужен период примерно 1 секунда. Для делителя на 16 в коде 1-2-4-8 можно применить что-нибудь типа К155/К555 ИЕ5 или ИЕ7 (совсем круто было бы сделать счетчик тоже на GAL, но это в следующий раз). В коробочке нашлась К555ИЕ7 (SN74LS193), значит так тому и быть. На вывод «R» подадим ноль, на выводы «V» и «-1» — единицу, на вывод «+1» — тактовые импульсы с NE555. Счетчик начал считать. Возьмем семисегментный индикатор с общим анодом и нашу GAL. Перед этим сотрем её и прошьем JEDEC файлом. Индикатор попался LTS-4801WC, OK. Выводы счетчика Q0,Q1,Q2,Q3 соединим со входами D0,D1,D2,D3 GAL, а выходы GAL – с катодами индикатора через 7 резисторов на 330 Ом.

Получается как-то так:

Заключение

Итак, мы окунулись в историю программируемых логических микросхем (PLD). Мы увидели, что за конструкцией PAL скрывается Древняя Могучая Теория. Выяснилось, что даже сейчас, вполне еще можно применять эти устройства в небольших самоделках. Мы рассмотрели вполне боевой «workflow», как это сделать. И да, PAL и GAL совместимы с олдовой теплой 5V TTL электроникой.

Конечно, в такой короткой статье невозможно отразить все аспекты. Вот кратко, про что мы не рассказали:

Не рассмотрели работу симулятора. В PALASM (2 и 4) встроен довольно мощный симулятор, практически язык программирования, с циклами, условными операторами и т.д.

Не рассмотрели построение на PALASM конечных автоматов. Как-нибудь в другой раз.

Не рассмотрели тонкости и ограничения оптимизации, но зато сделали оптимизацию вручную, по карте Карно. Это исключительно в ретро-целях! Сейчас так никто уже не делает (как и сами разработки на PAL).

Не ответили на вопрос: можно ли вводить в PALASM выражения не в ДНФ? Конечно можно. Если выражение синтаксически корректно, PALASM скорее всего его поймет. Но внутри все равно преобразует в ДНФ для воплощения в перемычках.

Не рассмотрели вопрос программирования (прошивки) исходных MMI PAL. Проблема здесь в том, что это однократно программируемые микросхемы и сейчас довольно сложно найти чистые PAL. И их не стереть. А программировались они специальным программатором (например, российский «Стерх» это умеет). Изначально у MMI был даже метод прошивать PAL как ПЗУ 512x4 на старых программаторах с помощью специальной «personality card» — у первых PAL было ровно 2048 перемычек, но ныне этот способ утрачен.

И еще много чего.