Предыдущий пост см. здесь.

Предсказание

В заключении, мы подходим к одному из наиболее важных применений линейной регрессии: предсказанию. Мы натренировали модель способную предсказывать вес олимпийских пловцов при наличии данных об их росте, половой принадлежности и годе рождения.

9-кратный олимпийский чемпион по плаванию Марк Шпитц завоевал 7 золотых медалей на Олимпийских играх 1972 г. Он родился в 1950 г. и, согласно веб-страницы Википедии, имеет рост 183 см. и вес 73 кг. Посмотрим, что наша модель предсказывает в отношении его веса.

Наша множественная регрессионная модель требует предоставить эти значения в матричной форме. Каждый параметр нужно передать в том порядке, в котором модель усвоила признаки, чтобы применить правильный коэффициент. После смещения вектор признаков должен содержать рост, пол и год рождения в тех же единицах измерения, в которых модель была натренирована:

Матрица ? содержит коэффициенты для каждого из этих признаков:

Предсказанием модели будет сумма произведений коэффициентов ? и признаков x в каждой строке:

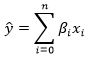
Поскольку матричное умножение производит каждый элемент в результате соответствующего сложения произведений строк и столбцов каждой матрицы, получение результата попросту сводится к перемножению транспонированной матрицы ? с вектором xspitz.

Напомним, что размерность итоговой матрицы будет числом строк из первой матрицы и числом столбцов из второй матрицы:

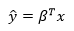
Здесь ?^Tx — это произведение матрицы размера 1 ? n и матрицы размера n ? 1. Результатом является матрица размера 1 ? 1:

Исходный код вычислений очень прост:

def predict(coefs, x): 
    '''функция предсказания'''
    return np.matmul(coefs, x.values) 

def ex_3_29():
    '''Вычисление ожидаемого веса спортсмена'''
    df = swimmer_data()
    df['бин_Пол'] = df['Пол'].map({'М': 1, 'Ж': 0}).astype(int) 
    df['Год рождения'] = df['Дата рождения'].map(str_to_year)
    X = df[['Рост, см', 'бин_Пол', 'Год рождения']] 
    X.insert(0, 'константа', 1.0)
    y = df['Вес'].apply(np.log) 
    beta = linear_model(X, y)
    xspitz = pd.Series([1.0, 183, 1, 1950]) # параметры Марка Шпитца
    return np.exp( predict(beta, xspitz) )  

84.20713139038605

Этот пример вернет число 84.21, которое соответствует ожидаемому весу 84.21 кг. Это намного тяжелее зарегистрированного веса Марка Шпитца 73 кг. Наша модель, похоже, не сработала как надо.

Интервал уверенности для конкретного предсказания

Ранее мы рассчитали интервалы уверенности для параметров популяции. Мы можем также построить интервал уверенности для отдельно взятого предсказания, именуемый интервалом предсказания, или интервалом изменений предсказанной величины. Интервал предсказания количественно определяет размер неопределенности в предсказании, предлагая минимальное и максимальное значение, между которыми истинное значение ожидаемо попадает с определенной вероятностью. Интервал предсказания для y? шире интервала уверенности для параметра популяции, такого как например, среднее значение ?. Это объясняется тем, что в интервале уверенности учитывается только неопределенность при оценке среднего значения, в то время как интервал предсказания также должен принимать в расчет дисперсию в y ^{от среднего значения.}

^{Линии интервала предсказания находятся дальше от оптимально подогнанной линии, чем линии интервала уверенности, и тем дальше, чем больше имеется точек данных. 95%-ый интервал предсказания – это площадь, в которую ожидаемо попадают 95% всех точек данных. В отличие от него, 95%-й интервал уверенности – это площадь, которая с 95%-й вероятностью содержит истинную линию регрессии.}

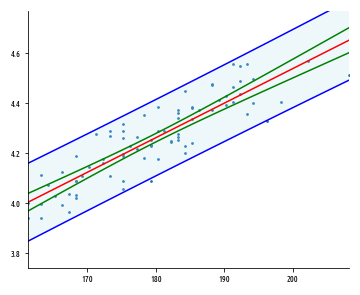
Приведенный выше график показывает связь между внешним интервалом предсказания и внутренним интервалом уверенности. Мы можем вычислить интервал предсказания, используя следующую ниже формулу:

Здесь y?_p — это предсказание, плюс или минус интервал. Мы пользуемся t-распределением, где степень свободы равна n - p, т.е. размер выборки минус число параметров. Это та же самая формула, которая ранее применялась при вычислении F-тестов. Хотя указанная формула, возможно, пугает своей сложностью, она относительно прямолинейно транслируется в исходный код, показанный в следующем ниже примере, который вычисляет 95%-ый интервал предсказания.

def prediction_interval(x, y, xp):
    '''Вычисление интервала предсказания'''
    xtx    = np.matmul(x.T, np.asarray(x))
    xtxi   = np.linalg.inv(xtx)  
    xty    = np.matmul(x.T, np.asarray(y)) 
    coefs  = linear_model(x, y) 
    fitted = np.matmul(x, coefs)
    resid  = y - fitted
    rss    = resid.dot(resid)  
    n      = y.shape[0]  # строки
    p      = x.shape[1]  # столбцы
    dfe    = n - p 
    mse    = rss / dfe
    se_y   = np.matmul(np.matmul(xp.T, xtxi), xp)
    t_stat = np.sqrt(mse * (1 + se_y))         # t-статистика
    intl   = stats.t.ppf(0.975, dfe) * t_stat   
    yp     = np.matmul(coefs.T, xp)
    return np.array([yp - intl, yp + intl])

Поскольку t-статистика параметризуется степенью свободы ошибки, она принимает в расчет присутствующую в модели неопределенность.

Если вместо интервала предсказания потребуется рассчитать интервал уверенности для среднего значения, мы попросту можем опустить прибавление единицы к se_y при вычислении t-статистики t_stat.

Приведенный выше исходный код можно использовать для генерирования следующего ниже графика, который показывает, как интервал предсказания изменяется вместе со значением независимой переменной:

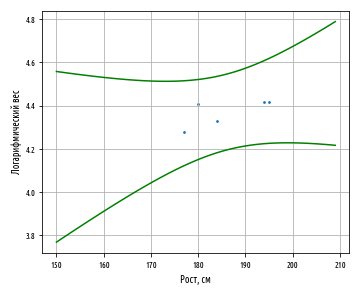
В приведенном выше графике модель тренируется на выборке из 5 элементов и показывает, как 95%-й интервал предсказания увеличивается по мере нашего движения дальше от среднего роста. Применив приведенную выше формулу к Марку Шпитцу, в результате получим следующее:

def ex_3_30():
    '''Интервал предсказания
       применительно к данным о Марке Шпитце'''
    df = swimmer_data()
    df['бин_Пол'] = df['Пол'].map({'М': 1, 'Ж': 0}).astype(int) 
    df['Год рождения'] = df['Дата рождения'].map(str_to_year)
    X = df[['Рост, см', 'бин_Пол', 'Год рождения']] 
    X.insert(0, 'константа', 1.0)
    y = df['Вес'].apply(np.log) 
    xspitz = pd.Series([1.0, 183, 1, 1950])  # данные М.Шпитца
    return np.exp( prediction_interval(X, y, xspitz) )

array([72.74964444, 97.46908087])

Этот пример возвращает диапазон между 72.7 и 97.4 кг., который как раз включает в себя вес Марка 73 кг., поэтому наше предсказание находится в пределах 95%-ого интервала предсказания. Правда оно лежит неудобно близко к границам диапазона.

Границы действия модели

Марк Шпитц родился в 1950 г., за несколько десятилетий до рождения самых возрастных пловцов на Олимпийских играх 2012 г. Пытаясь предсказать вес Марка, используя его год рождения, мы виноваты в том, что пытаемся экстраполировать слишком далеко за пределы наших тренировочных данных. Мы превысили границы действия нашей модели.

Есть и вторая причина, по которой этот результат сопряжен с проблемами. Наши данные полностью основаны на пловцах, которые соревнуются в наши дни на уровне международных стандартов, тогда как Марк не участвовал в соревнованиях уже много лет. Другими словами, Марк теперь не является частью популяции, на которой мы натренировали нашу модель. В целях исправления обеих этих проблем нам нужно поискать подробную информацию о Марке в 1979 г., когда он еще участвовал в соревнованиях по плаванию.

Согласно данным, в 1972 г. 22-летний Марк Шпитц имел рост 185 см. и весил 79 кг.

^{Отбор верных признаков — это одна из самых важных предпосылок для получения хороших результатов от любого алгоритма предсказания.}

Следует отбирать признаки не только, опираясь на их предсказательную силу, но и на их актуальность для моделируемой области.

Окончательная модель

Хотя наша модель имеет чуть более низкий R², давайте натренируем ее повторно, взяв в качестве признака возраст вместо года рождения. Это позволит нам легко предсказывать веса для прошлых и будущих ранее не встречавшихся данных, т.к. она ближе моделирует переменную, которая, как мы полагаем, имеет причинно-следственную связь с весом.

Модель произведет ? приблизительно с такими значениями:

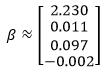
Наши признаки для Марка на играх 1972 г. таковы:

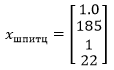
Эти признаки можно использовать для предсказания его соревновательного веса при помощи приведенного ниже примера:

def ex_3_32():
    '''Окончательная модель для предсказания 
       соревновательного веса'''
    df = swimmer_data()
    df['бин_Пол'] = df['Пол'].map({'М': 1, 'Ж': 0}).astype(int) 
    X = df[['Рост, см', 'бин_Пол', 'Возраст']] 
    X.insert(0, 'константа', 1.0)
    y = df['Вес'].apply(np.log) 

    beta = linear_model(X, y)
    # предсказать вес Марка Шпитца
    xspitz = pd.Series([1.0, 185, 1, 22]) 
    return np.exp( predict(beta, xspitz) )

78.46882772630318

Пример возвращает число 78.47, т.е. предсказывает вес 78.47 кг. Теперь результат находится очень близко к истинному соревновательному весу Марка, равному 79 кг.

Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги. 

Резюме

В этой серии постов мы узнали о том, как определять наличие общей линейной связи между двумя и более переменными. Мы увидели, как выражать силу их корреляции при помощи корреляции Пирсона r и насколько хорошо линейная модель объясняет вариацию при помощи коэффициентов детерминации R² и R?². Мы также выполнили проверку статистических гипотез и рассчитали интервалы уверенности, чтобы вывести диапазон истинного популяционного параметра ? для корреляции.

Определив корреляцию между переменными, мы смогли построить предсказательную модель с использованием регрессии методом обычных наименьших квадратов и простых функций Python. Затем мы обобщили наш подход, воспользовавшись для этого матричной функциональностью библиотек pandas и numpy и нормальным уравнением. Эта простая модель продемонстрировала принципы машинного усвоения закономерностей путем определения модельных параметров ?, извлеченных из выборочных данных, которые могут использоваться для выполнения предсказаний. Наша модель смогла предсказать ожидаемый вес нового атлета, который полностью попадал в пределы интервала предсказания для истинного значения.