Пост №3 для начинающих посвящен генерированию распределений, их свойствам, а также графикам для их сопоставительного анализа. Предыдущий пост см. здесь.
Булочник и Пуанкаре
Существует легенда, почти наверняка апокрифическая, которая дает возможность детальнее рассмотреть вопрос о том, каким образом центральная предельная теорема позволяет рассуждать о принципе формирования статистических распределений. Она касается прославленного французского эрудита XIX-ого века Анри Пуанкаре, который, как гласит легенда, в течение одного года каждый день занимался тем, что взвешивал свежую буханку хлеба.
В те времена хлебопекарное ремесло регламентировалось государством, и Пуанкаре обнаружил, что, хотя результаты взвешивания буханок хлеба подчинялись нормальному распределению, пик находился не на публично афишируемом 1 кг, а на 950 г. Он сообщил властям о булочнике, у которого он регулярно покупал хлеб, и тот был оштрафован. Такова легенда ;-).
В следующем году Пуанкаре продолжил взвешивать буханки хлеба того же булочника. Он обнаружил, что среднее значение теперь было равно 1 кг, но это распределение больше не было симметричным вокруг среднего значения. Теперь оно было смещено вправо. А это соответствовало тому, что булочник теперь давал Пуанкаре только самые тяжелые из своих буханок хлеба. Пуанкаре снова сообщил о булочнике властям, и булочник был оштрафован во второй раз.
Было ли это на самом деле или нет здесь не суть важно; этот пример всего лишь служит для того, чтобы проиллюстрировать ключевой момент — статистическое распределение последовательности чисел может сообщить нам нечто важное о процессе, который ее создал.
Генерирование распределений
В целях развития нашего интуитивного понимания относительно нормального распределения и дисперсии, давайте смоделируем честного и нечестного булочников, и для этого воспользуемся функцией генерирования нормально распределенных случайных величин stats.norm.rvs. (rvs от англ. normal variates, т.е. нормально-распределенные случайные величины). Честного булочника можно смоделировать в виде нормального распределения со средним значением 1000, что соответствует справедливой буханке хлеба весом 1 кг. При этом мы допустим наличие дисперсии в процессе выпекания, которая приводит к стандартному отклонению в 30г.
def honest_baker(mu, sigma):
'''Модель честного булочника'''
return pd.Series( stats.norm.rvs(loc, scale, size=10000) )
def ex_1_18():
'''Смоделировать честного булочника на гистограмме'''
honest_baker(1000, 30).hist(bins=25)
plt.xlabel('Честный булочник')
plt.ylabel('Частота')
plt.show()Приведенный выше пример построит гистограмму, аналогичную следующей:

Теперь смоделируем булочника, который продает только самые тяжелые буханки хлеба. Мы разобьем последовательность на группы по тринадцать элементов (на «чертовы дюжины») и отберем максимальное значение в каждой:
def dishonest_baker(mu, sigma):
'''Модель нечестного булочника'''
xs = stats.norm.rvs(loc, scale, size=10000)
return pd.Series( map(max, bootstrap(xs, 13)) )
def ex_1_19():
'''Смоделировать нечестного булочника на гистограмме'''
dishonest_baker(950, 30).hist(bins=25)
plt.xlabel('Нечестный булочник')
plt.ylabel('Частота')
plt.show()Приведенный выше пример создаст гистограмму, аналогичную следующей:
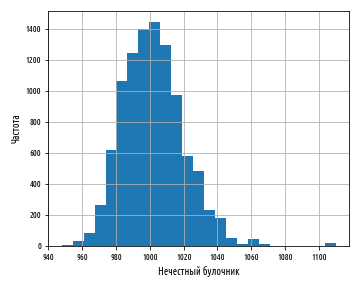
Совершенно очевидно, что эта гистограмма выглядит не совсем так, как другие, которые мы видели. Среднее значение по-прежнему равно 1 кг, но разброс значений вокруг среднего больше не является симметричным. Мы говорим, что эта гистограмма показывает смещенное нормальное распределение.
Асимметрия
Асимметрией называется смещение распределения относительно ее моды. Отрицательная асимметрия, или левое смещение кривой, указывает на то, что площадь под графиком больше на левой стороне моды. Положительная асимметрия, или правое смещение кривой, указывает на то, что площадь под графиком больше на правой стороне моды.
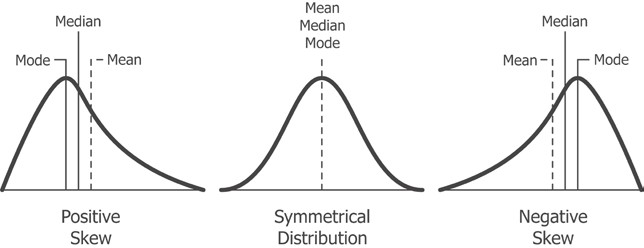
Библиотека pandas располагает функцией skew для измерения асимметрии:
def ex_1_20():
'''Получить коэффициент асимметрии нормального распределения'''
s = dishonest_baker(950, 30)
return { 'среднее' : s.mean(),
'медиана' : s.median(),
'асимметрия': s.skew() }{'асимметрия': 0.4202176889083849,
'медиана': 998.7670301469957,
'среднее': 1000.059263920949}Приведенный выше пример показывает, что коэффициент асимметрии в выпечке от нечестного булочника составляет порядка 0.4. Этот коэффициент количественно определяет степень скошенности, которая видна на гистограмме.
Графики нормального распределения
Ранее в этой серии постов мы познакомились с квантилями как средством описания статистического распределения данных. Напомним, что функция quantile принимает число между 0 и 1 и возвращает значение последовательности в этой точке. 0.5-квантиль соответствует значению медианы.
Изображение квантилей данных относительно квантилей нормального распределения позволяет увидеть, каким образом наши измеренные данные соотносятся с теоретическим распределением. Подобные графики называются квантильными графиками, или диаграммами квантиль-квантиль, графиками Q-Q, от англ. Q-Q plot. Они предоставляют быстрый и интуитивно понятный способ определить степень нормальности статистического распределения. Для данных, которые близки к нормальному распределению, квантильный график покажет прямую линию. Отклонения от прямой линии показывают, каким образом данные отклоняются от идеализированного нормального распределения.
Теперь построим квантильные графики для честного и нечестного булочников. Функция qqplot принимает список точек данных и формирует график выборочных квантилей, отображаемых относительно квантилей из теоретического нормального распределения:
def qqplot( xs ):
'''Квантильный график (график квантиль-квантиль, Q-Q plot)'''
d = {0:sorted(stats.norm.rvs(loc=0, scale=1, size=len(xs))),
1:sorted(xs)}
pd.DataFrame(d).plot.scatter(0, 1, s=5, grid=True)
df.plot.scatter(0, 1, s=5, grid=True)
plt.xlabel('Квантили теоретического нормального распределения')
plt.ylabel('Квантили данных')
plt.title ('Квантильный график', fontweight='semibold')
def ex_1_21():
'''Показать квантильные графики
для честного и нечестного булочников'''
qqplot( honest_baker(1000, 30) )
plt.show()
qqplot( dishonest_baker(950, 30) )
plt.show()Приведенный выше пример создаст следующие ниже графики:

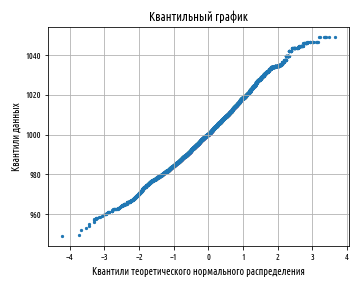
Выше показан квантильный график для честного булочника. Далее идет квантильный график для нечестного булочника:
Тот факт, что линия имеет изогнутую форму, показывает, что данные положительно асимметричны; наклон в другую сторону будет означать отрицательную асимметрию. Квантильный график в сущности позволяет легко различить целый ряд отклонений от стандартного нормального распределения, как показано на следующем ниже рисунке:

Надписи: нормально распределенные, тяжелые хвосты, легкие хвосты, скошенность влево, скошенность вправо, раздельные кластеры
Квантильные графики сопоставляют статистическое распределение честного и нечестного булочника с теоретическим нормальным распределением. В следующем разделе мы сравним несколько альтернативных способов визуального сопоставления двух (или более) измеренных последовательностей значений.
Технические приемы сопоставительной визуализации
Квантильные графики дают замечательную возможность сопоставить измеренное эмпирическое (выборочное) распределение с теоретическим нормальным распределением. Однако если мы хотим сопоставить друг другу два или более эмпирических распределения, то графики нормального распределения для этого не подойдут. Впрочем, у нас есть несколько других вариантов, как показано в следующих двух разделах.
Коробчатые диаграммы
Коробчатые диаграммы, или диаграммы типа «ящик с усами», — это способ визуализации таких описательных статистик, как медиана и дисперсия. Мы можем сгенерировать их с помощью следующего исходного кода:
def ex_1_22():
'''Показать коробчатую диаграмму
с данными честного и нечестного булочников'''
d = {'Честный булочник' :honest_baker(1000, 30),
'Нечестный булочник':dishonest_baker(950, 30)}
pd.DataFrame(d).boxplot(sym='o', whis=1.95, showmeans=True)
plt.ylabel('Вес буханки (гр.)')
plt.show()Этот пример создаст следующую диаграмму:

Ящики в центре диаграммы представляют интерквартильный размах. Линия поперек ящика — это медиана. Большая точка — это среднее. Для честного булочника линия медианы проходит через центр окружности, показывая, что среднее и медиана примерно одинаковые. Для нечестного булочника среднее отодвинуто от медианы, что указывает на смещение.
Усы показывают на диапазон данных. Выбросы представлены полыми кругами. Всего одна диаграмма позволяет яснее увидеть расхождение между двумя статистическими распределениями, чем рассматривать их отдельно на гистограмме или квантильном графике.
Интегральные функции распределения
Интегральные функции распределения (ИФР), также именуемые кумулятивными функциями распределения, от англ. Cumulative Distribution Function (CDF), описывают вероятность, что значение, взятое из распределения, будет меньше x. Как и все распределения вероятностей, их значения лежат в диапазоне между 0 и 1, где 0 — это невозможность, а 1 — полная определенность. Например, представьте, что я собираюсь бросить шестигранный кубик. Какова вероятность, что выпадет значение меньше 6?
Для уравновешенного кубика вероятность выпадения пятерки или меньшего значения равна 5/6. И наоборот, вероятность, что выпадет единица, равна всего 1/6. Тройка или меньше соответствуют равным шансам — то есть вероятности 50%.
ИФР выпадения чисел на кубике следует той же схеме, что и все ИФР — для чисел на нижнем краю диапазона ИФР близка к нулю, что соответствует низкой вероятности выбора чисел в этом диапазоне или ниже. На верхнем краю диапазона ИФР близка к единице, поскольку большинство значений, взятых из последовательности, будет ниже.
ИФР и квантили тесно друг с другом связаны — ИФР является инверсией квантильной функции. Если 0.5-квантиль соответствует значению 1000, тогда ИФР для 1000 составляет 0.5.
Подобно тому, как функция pandas quantile позволяет нам отбирать значения из распределения в конкретных точках, эмпирическая ИФР empirical_cdf позволяет нам внести значение из последовательности и вернуть значение в диапазоне между 0 и 1. Это функция более высокого порядка, т.е. она принимает значение (в данном случае последовательность значений) и возвращает функцию, которую потом можно вызывать, сколько угодно, с различными значениями на входе, и возвращая ИФР для каждого из них.
Функции более высокого порядка — это функции, которые принимают или возвращают функции.
Построим график ИФР одновременно для честного и нечестного булочников. Для этих целей можно воспользоваться функцией библиотеки pandas построения двумерного графика plot для визуализации ИФР, изобразив на графике исходные данные — то есть выборки из распределений честного и нечестного булочников — в сопоставлении с вероятностями, вычисленными относительно эмпирической ИФР. Функция plot ожидает, что значения x и значения y будут переданы в виде двух раздельных последовательностей значений. Для этих целей мы воспользуемся конструктором кадра данных pandas DataFrame.
Чтобы изобразить оба распределения на одном графике, мы должны передать функции plot несколько серий. Для многих своих графиков pandas предоставляет функции, которые позволяют добавлять дополнительные серии. В случае с функцией plot мы можем присвоить указатель на создаваемый график, присвоив временной переменной (ax) результат первого вызова функции plot, и затем при повторных вызовах указывать эту переменную в именованном аргументе функции (ax=ax). Можно также передать необязательную метку серии. Мы выполним это в следующем ниже примере, чтобы на готовом графике отличить две серии друг от друга. Сначала определим универсальную функцию построения эмпирической ИФР против теоретической, которая получает на вход кортеж из двух серий (tp[1] и tp[3]) и их названий и метки осей, и затем вызовем ее:
def empirical_cdf(x):
'''Вернуть эмпирическую ИФР для x'''
sx = sorted(x)
return pd.DataFrame( {0: sx, 1:sp.arange(len(sx))/len(sx)} )
def ex_1_23():
'''Показать графики эмпирической ИФР
честного булочника в сопоставлении с нечестным'''
df = empirical_cdf(honest_baker(1000, 30))
df2 = empirical_cdf(dishonest_baker(950, 30))
ax = df.plot(0, 1, label='Честный булочник')
df2.plot(0, 1, label='Нечестный булочник', grid=True, ax=ax)
plt.xlabel('Вес буханки')
plt.ylabel('Вероятность')
plt.legend(loc='best')
plt.show()Приведенный выше пример сгенерирует следующий график:
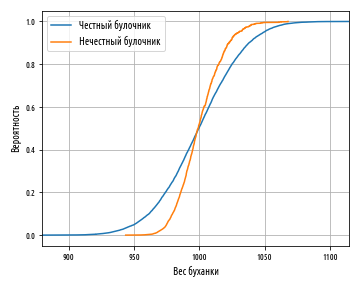
Несмотря на то, что этот график выглядит совсем по-другому, он в сущности показывает ту же самую информацию, что и коробчатая диаграмма. Мы видим, что две линии пересекаются примерно в медиане 0.5, соответствующей 1000 гр. Линия нечестного булочника обрезается в нижнем хвосте и удлиняется на верхнем хвосте, что соответствует асимметричному распределению.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
Следующая часть, часть 4, серии постов «Python, исследование данных и выборы» посвящена техническим приемам визуализации данных.


kzone
RVs - Random Variables