
В этой статье мы рассмотрим, что такое классификатор, поговорим о мультиклассовой классификации с помощью нейронных сетей. Затем, ознакомившись с контекстом перейдем к основному топику поста — к Log-Sum-Exp Trick. Напишем формулы и разберемся, как этот трюк помогает избежать переполнения чисел с плавающей точкой.
Логистическая регрессия
В классическом машинном обучение существует метод классификации под названием логистическая регрессия. Классификатор на основе логистической регрессии, в обычном случае, призван разделять данные на два класса. Например, классификатор электронной почты может выдавать значение 0.9, что может означать: 90% вероятность, письмо спам, и 10% — не спам. При этом сумма вероятностей всегда даёт единицу. Логистическая регрессия выдаёт такие вероятности на основе выхода сигмоидной функции.
Здесь возникают следующие вопросы. Как действовать, если наши данные нужно разделять на более, чем два класса? Какую функцию использовать, для того, чтобы выходы классификатора можно было трактовать как вероятности?
Мультиклассовые нейронные сети
В качестве классификатора, выдающего сразу несколько вероятностей, давайте рассмотрим нейронную сеть. Такие нейронные сети делают предсказания с помощью функции софтмакс.
В формуле выше — выходные значения нейронной сети для каждого класса,
— преобразованные с помощью софтмакс вероятности.
Софтмакс генерализует задачу получения вероятностей, когда выходов у классификатора больше двух.
Например, если мы обучили классификатор на изображениях, определять что изображено на картинке, то мы можем увидеть что-то похожее на следующее:
так схематично изображается применение софтмакса к выходам нейронной сети,
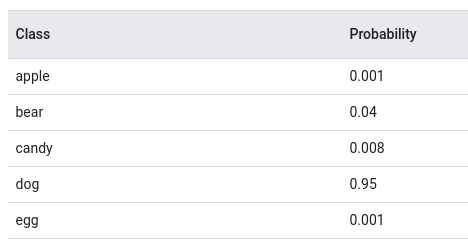
а так будет выглядеть распределение вероятностей, они в сумме дают единицу (источник).
Проблема переполнения при вычислении Softmax
Логиты, приходящие из нейронной сети, могут принимать произвольные значения на вещественной прямой. Рассмотрим, что будет если в Python мы попытаемся вычислить софтмакс для третьей компоненты заданного вектора:
import numpy as np
x = np.array([-100, 1000, -100, 5, 10, 0.001])
exp_x = np.exp(x)
print("Возведение в степень X: ", "\n", exp_x)
print("Сумма экспонент: ", "\n", np.sum(exp_x))
print("Третья вероятность: ", np.exp(x[3]) / np.sum(exp_x))
Вывод:
Возведение в степень X:
[3.72007598e-44 inf 3.72007598e-44 1.48413159e+02
2.20264658e+04 1.00100050e+00]
Сумма экспонент: inf
Третья вероятность: 0.0
Видим, что значения 1000 приводит к переполнению и это губит всю дальнейшую нормализацию.
Log-Sum-Exp
Для решения проблемы поставленной выше предлагается воспользоваться функцией
— Log-Sum-Exp функция.
Её определение вытекает из названия — это последовательное применение к входному аргументу: экспоненты, суммирования и логарифмирования. Часто можно увидеть, что эту функцию называют дифференцируемым аналогом функции максимума от нескольких переменных. Дифференцируемость — крайне полезное для поиска экстремумов свойство.
 (источник)
(источник)Как видно на картинке выше, lse(x) всюду гладкая, в отличии от max(x) функция.
Вариант Log-Sum-Exp без переполнения
Если попытаться вычислить функцию LSE от вектора x, то мы так же столкнемся с проблемой переполнения, поскольку в сумме участвуют экспоненты произвольной, возможно большой, степени. Путём преобразований, основанных на свойствах функции можно избавиться от проблемы переполнения.
Пусть результат выполнения имеет значение
, тогда мы можем записать следующее уравнение:
Применим экспоненту к обоим частя уравнения:
Время трюка. Пусть тогда вынесем из каждого слагаемого
:
Теперь проверим на практике новую формулу:
import numpy as np
x = np.array([11, 12, -1000, 5, 10, 0.001])
y = np.array([-1000, 1000, -1000, 5, 10, 0.001])
def LSE_initial(x):
return np.log(np.sum(np.exp(x)))
def LSE_modified(x):
c = np.max(x)
return c + np.log(np.sum(np.exp(x - c)))
# с экспонентами, не приводящими к переполнению
print('Исходная LSE(x): ', LSE_initial(x))
print('Преобразованная LSE(x): ', LSE_modified(x))
# с экспонентой в 1000й степени
print('Исходная LSE(y): ', LSE_initial(y))
print('Преобразованная LSE(y): ', LSE_modified(y))Вывод:
Исходная LSE(x): 12.408216490736713
Преобразованная LSE(x): 12.408216490736713
Исходная LSE(y): inf
Преобразованная LSE(y): 1000.0Видно, что даже в случае, когда одно из слагаемых обращается в float inf, модифицированный вариант lse(x) даёт верный результат.
Log-Sum-Exp Trick
Теперь перейдём непосредственно к трюку. Наша исходная задача состоит в том, чтобы вычислить софтмакс для набора вещественных значений, не получая при этом неправильные результаты из-за переполнения.
Чтобы этого добиться, давайте приведем функцию софтмакс к виду, зависящему от .
Пусть в формуле софтмакс равно
, тогда наше равенство примет следующий вид:
Применим ряд преобразований:
Получается, что вместо вычисления исходного примера можно вычислить следующее:
Применим новую формулу для вычисления софтмакса:
import numpy as np
x = np.array([11, 12, -1000, 5, 10, 0.001])
y = np.array([-1000, 1000, -1000, 5, 10, 0.001])
def softmax_initial(x):
return np.exp(x) / np.sum(np.exp(x))
def LSE(x):
c = np.max(x)
return c + np.log(np.sum(np.exp(x - c)))
def softmax_modified(x):
return np.exp(x - LSE(x))
# с экспонентами, не приводящими к переполнению
print('Исходный Softmax(x): ', softmax_initial(x))
print('Преобразованный Softmax(x): ', softmax_modified(x))
print('Суммы вероятностей: {} {}\n'.format(np.sum(softmax_initial(x)), np.sum(softmax_modified(x))))
# с экспонентой в 1000й степени
print('Исходный Softmax(y): ', softmax_initial(y))
print('Преобразованный Softmax(y): ', softmax_modified(y))
print('Суммы вероятностей: {} {}'.format(np.sum(softmax_initial(y)), np.sum(softmax_modified(y))))Вывод:
Исходный Softmax(x): [2.44579103e-01 6.64834933e-01 0.00000000e+00 6.06250985e-04
8.99756239e-02 4.08897394e-06]
Преобразованный Softmax(x): [2.44579103e-01 6.64834933e-01 0.00000000e+00 6.06250985e-04
8.99756239e-02 4.08897394e-06]
Суммы вероятностей: 0.9999999999999999 1.0000000000000004
Исходный Softmax(y): [ 0. nan 0. 0. 0. 0.]
Преобразованный Softmax(y): [0. 1. 0. 0. 0. 0.]
Суммы вероятностей: nan 1.0Здесь, аналогично результатам с преобразованным lse(x), видно, что модифицированная версия софтмакса стабильнее, и не страдает от переполнения при вычислении. Сумма вероятностей, полученных из софтмакс, даёт единицу, на всех примерах векторов. Такое поведение и ожидается от этой функции.
Заключение
В посте мы познакомились с несколькими широко используемыми в машинном обучении функциями. Обсудили поверхностно как работает множественный классификатор на основе нейронной сети. И самое главное, разобрались как избежать неправильных результатов, когда нужно выдавать вероятности отнесения к определенному классу, у такой нейронной сети.
Статья была подготовлена в рамках курса «Математика для Data Science». Также предлагаю всем желающим посмотреть запись бесплатного демоурока про линейные пространства и отображения.
— СМОТРЕТЬ ДЕМОУРОК


AC130
Почему просто не вычесть константу c из всех x_i перед взятием софтмакса? Вычитание любой константы из вектора не должно менять значение софтмакса так как это эквивалентно сокращению дроби в софтмаксе на exp( c ).
leok
Ровно это функция LSE в коде выше и делает.
AC130
Речь идёт о том, чтобы сделать «ровно это» не вводя функцию LSE.