Чтобы лучше понять глубокое обучение, Data Scientist из Hewleet Packard написал нейросеть только при помощи NumPy. Знать свои инструменты необходимо любому специалисту, поэтому наш курс по науке о данных включает раздел «Математика для Data Science». Под катом вы найдёте не только реализацию нейронной сети. Статья начинается со знакомства с книгой автора, которая, по его словам, будет полезна, если вы хотите создать достойное портфолио Machine Learning.

Книга по ссылке ниже — продолжение этой статьи. В ней рассказывается о реализации проектов нейронных сетей в областях распознавания лиц, анализа настроений, удаления шума и т. д. Каждая глава освещает отдельную архитектуру нейросети: это свёрточные сети, сети долгой краткосрочной памяти и сиамские нейронные сети. Если вы хотите создать сильное портфолио в области ML, включающее проекты глубокого обучения, присмотритесь к этой книге, скачать которую вы можете здесь.

Что такое нейросеть?

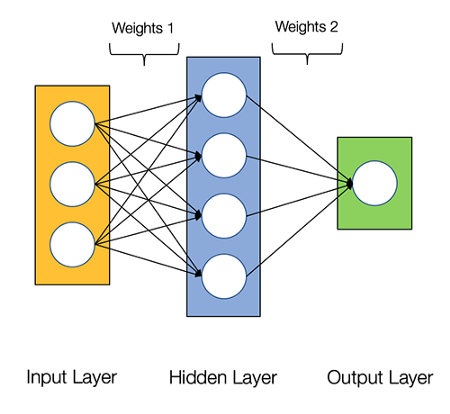
Большинство вводных текстов приводят аналогию с мозгом. Но я считаю, что проще описать нейросеть как математическую функцию, которая отображает данное входное значение на желаемое выходное. Вот из каких компонентов состоит нейросеть:

• Входной слой — x.

• Произвольное число скрытых слоёв.

• Выходной слой — ŷ.

• Множество весов и смещений между всеми слоями — W и b.

• Выбираемой нами функция активации для каждого слоя — σ. Здесь воспользуемся сигмоидной функцией потерь.

Обратите внимание: входной слой не учитывается в подсчёте количества слоёв.

Создать класс нейросети на Python просто:

class NeuralNetwork:
    def __init__(self, x, y):
        self.input      = x
        self.weights1   = np.random.rand(self.input.shape[1],4) 
        self.weights2   = np.random.rand(4,1)                 
        self.y          = y
        self.output     = np.zeros(y.shape)

Обучаем сеть

Вот её вывод в виде формулы:

Веса W и смещения b — это только переменные, которые влияют на вывод — ŷ. Естественно, правильность значений и весов предопределяется предсказательной силой. Процесс тонкой настройки весов и смещений на основании входных данных известен как обучение нейронной сети. Каждая итерация обучения состоит из:

• Расчёта спрогнозированного вывода ŷ, известного как прямое распространение.

• Обновления весов и смещений, известного как обратное распространение.

Диаграмма ниже иллюстрирует обучение:

Прямое распространение

Как мы видим, прямое распространение — это просто. Вывод нашей нейросети будет таким:

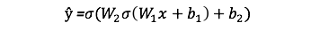
Добавим прямое распространение в код. Для простоты возьмём смещение, равное нулю:

class NeuralNetwork:
    def __init__(self, x, y):
        self.input      = x
        self.weights1   = np.random.rand(self.input.shape[1],4) 
        self.weights2   = np.random.rand(4,1)                 
        self.y          = y
        self.output     = np.zeros(self.y.shape)

    def feedforward(self):
        self.layer1 = sigmoid(np.dot(self.input, self.weights1))
        self.output = sigmoid(np.dot(self.layer1, self.weights2))

​Однако мы по-прежнему нуждаемся в оценке точности предсказаний. Именно в этом поможет функция потерь.

Функция потерь

Функций потерь множество: диктовать её выбор должна природа проблемы. Здесь задействуем функцию суммы квадратов ошибок.

Это просто разница между каждым спрогнозированным и реальным значениями. Она возводится в квадрат, чтобы получить абсолютное значение. Цель обучения — найти лучшее множество значение весов и смещений, которое минимизирует функцию потерь.

Обратное распространение

Теперь, когда мы измерили ошибку предсказаний (потерю), нужно найти способ распространить ошибку обратно, обновив при этом смещения и веса. Чтобы узнать полученную сумму, мы должны найти производную функции потерь. Напомню, что производная функции — это просто её уклон.

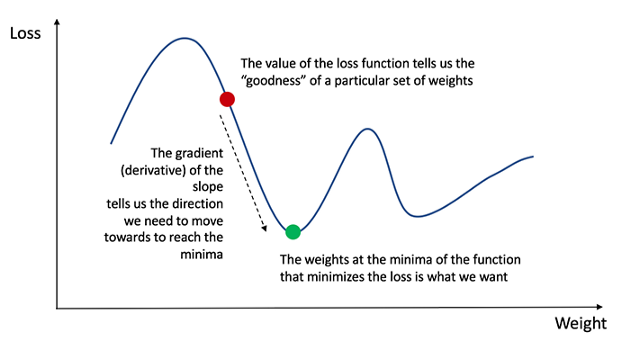
Имея производную, мы можем обновлять веса и смещения, увеличивая или уменьшая её. Смотрите график выше. Метод известен как градиентный спуск. Однако нельзя напрямую рассчитать производную функции потерь относительно весов и смещений: уравнение просто не содержит их. Чтобы вычислить производную, понадобится правило цепочки:

Правило цепочки для вычисления производной относительно весов и смещений.

Обратите внимание: для простоты я показываю частную производную, предполагая сеть в один слой.

Жутковато, но мы получили то, что нужно — производную относительно весов и смещений, так что можно соответствующим образом настроить веса. Добавим обратное распространение в код:

class NeuralNetwork:
    def __init__(self, x, y):
        self.input      = x
        self.weights1   = np.random.rand(self.input.shape[1],4) 
        self.weights2   = np.random.rand(4,1)                 
        self.y          = y
        self.output     = np.zeros(self.y.shape)

    def feedforward(self):
        self.layer1 = sigmoid(np.dot(self.input, self.weights1))
        self.output = sigmoid(np.dot(self.layer1, self.weights2))

    def backprop(self):
        # application of the chain rule to find derivative of the loss function with respect to weights2 and weights1
        d_weights2 = np.dot(self.layer1.T, (2*(self.y - self.output) * sigmoid_derivative(self.output)))
        d_weights1 = np.dot(self.input.T,  (np.dot(2*(self.y - self.output) * sigmoid_derivative(self.output), self.weights2.T) * sigmoid_derivative(self.layer1)))

        # update the weights with the derivative (slope) of the loss function
        self.weights1 += d_weights1
        self.weights2 += d_weights2

​Чтобы лучше понять приложение интегрального исчисления и правило цепочки в обратном распространении, я настоятельно рекомендую это учебное руководство от 3Blue1Brown:

Соберём всё воедино

У нас есть код обратного и прямого распространений. Посмотрим, как работает нейросеть. Вот набор данных:

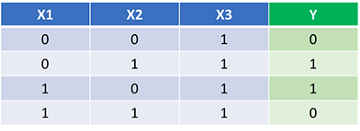
Сеть должна представить идеальный для этой функции набор весов и смещений. Замечу, что определять веса только через исследование — не совсем тривиально. Обучим сеть на 1500 итерациях и посмотрим, что произойдёт. Наблюдая за потерями на графике ниже, мы ясно увидим монотонное убывание к минимуму. Это соответствует алгоритму градиентного спуска, о котором говорилось выше.

Посмотрим на вывод:

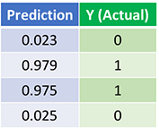
Мы сделали это! Обратное и прямое распространения с успехом натренировали сеть, а предсказания сошлись с истинными значениями. Отмечу, что между предсказанными и истинными значениями есть небольшая разница. Она желательна, поскольку предотвращает переобучение и позволяет нейросети лучше обобщать данные, которых она не видела.

Что дальше?

К счастью для нас, это далеко не конец путешествия. О нейронных сетях и глубоком обучении ещё многое предстоит изучить. Например:

• Какие функции активации, кроме сигмоидной, можно использовать?

• Как работать со скоростью обучения нейросетей?

• Как при помощи CNN классифицировать изображения?

Продолжить изучение Machine Learning и Data Science вы сможете на наших курсах. Также вы можете узнать, как мы готовим специалистов в других направлениях.

Data Science и Machine Learning

• Профессия Data Scientist

• Профессия Data Analyst

• Курс «Математика для Data Science»

• Курс «Математика и Machine Learning для Data Science»

• Курс по Data Engineering

• Курс «Machine Learning и Deep Learning»

• Курс по Machine Learning

Python, веб-разработка

• Профессия Fullstack-разработчик на Python

• Курс «Python для веб-разработки»

• Профессия Frontend-разработчик

• Профессия Веб-разработчик

Мобильная разработка

• Профессия iOS-разработчик

• Профессия Android-разработчик

Java и C#

• Профессия Java-разработчик

• Профессия QA-инженер на JAVA

• Профессия C#-разработчик

• Профессия Разработчик игр на Unity

От основ — в глубину

• Курс «Алгоритмы и структуры данных»

• Профессия C++ разработчик

• Профессия Этичный хакер

А также:

• Курс по DevOps