
В предыдущей статье были рассмотрены простые шифры, использующие алфавиты естественных языков (ЕЯ). Автоматическая обработка сообщений в компьютерных и сетях связи предусматривает использование искусственных языков (ИЯ), что более эффективно во многих отношениях. Ранее описывалась классификация шифров и для некоторых из них было показано, как они применяются в области информационной безопасности для решения триединой задачи информационной безопасности: конфиденциальности, целостности и доступности. Здесь продолжим рассмотрение, но для более сложных современных шифров
Векторно-матричные преобразования
В некоторых шифрах замены используют в качестве преобразования сообщений квадратные матрицы прямую и обратную, например, L[3×3] размерности 3×3;
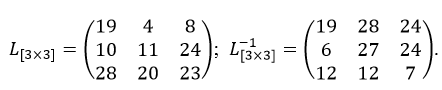

Процедура шифрования исходного оцифрованного текста состоит в последовательном умножении всех триад хi ИТ справа на шифрующую матрицу по mod 32

Получили шифртекст в триадах с переходом от числового представления к буквам
у1 = НЦЖ; у2= ЕОВ; у3 = ФУТ; у4 = ЫЧИ; у5 =КФА; у6 = ФАЭ. Процедура расшифрования шифрованного текста состоит в последовательном умножении всех триад уi ИТ справа на матрицу обратную к шифрующей матрице по mod 32

В результате расшифрования получаем открытый текст. Отметим один существенный недостаток шифра. Такой шифр при любом ключе сохраняет неподвижным нулевой вектор, что, конечно, является уязвимостью. Этот недостаток устраним путем перехода от линейных преобразований к аффинным, которые описываются формулами с прямой y<3> = L[3×3] (x<3>) и обратной матрицами х<3> = L-1[3×3] (y<3>– a<3>) преобразования. Устранение недостатка возможно введением вектора сдвига, что показано ниже.
Шифр аффинного преобразования
Пример 1. Шифрование с использованием аффинного преобразования сообщения.
Пусть в качестве открытого текста взято слово КРИПТОГРАФИЯ разбитое на триады. После зашифрования получается текст ПЮП РОЙ ИШЛ ЕЮШ.
Находим цифровое представление векторов открытого текста:
КРИ = х1 = (10, 16, 8), ПТО = х2 = (15, 18, 14), ГРА = x3 = (3,16, 0), ФИЯ = x4 = (20, 8, 31). Шифрованного текста:
ПЮП = y1 = (15,30,15), РОЙ = y2 = (16,14, 9), ИШЛ = y3 = (8, 24,11), ЕЮШ = y4 = (5,30,24).
Теперь перейдем к определению а вектора аффинного сдвига
Он находится как линейная комбинация входных векторов, представляющая нулевой вектор, т.е. решаем над кольцом Z/32Z систему линейных уравнений относительно переменных a, b, c, d: ax1+bx2+cx3 + dx4 = 0. Здесь 0 – нулевой вектор, а
x1, x2, x3, x4 – входные векторы триады- открытого текста. Получаем решение в виде
b = 8a, c = 10a, d = 24a, где а – произвольный ненулевой элемент кольца Z/32Z. Тогда уравнение шифрования для такой линейной комбинации входных текстов запишется в виде (а -вектор сдвига):
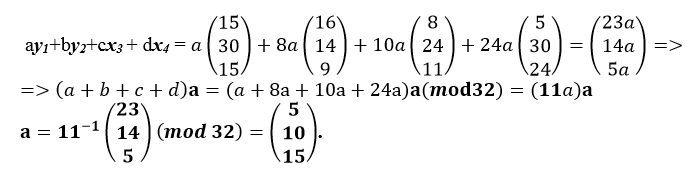
Теперь находим матрицу L[3×3]. Для этого надо перейти к центрированным выходным векторам (ШТ), т.е. к шифрованным векторам, смещенным на вектор сдвига yi' = yi - а:
y1' = (10, 20,0), y2' = (11, 4, 26), y3' = (3, 14, 28), y4'= (0, 20, 9). Находим значения этих векторов (результатов центрирования):
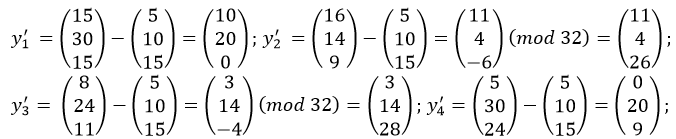


Объединяя строки получим матрицу аффинного преобразования, используемую в шифре. Следующий пример иллюстрирует современный шифр, являющийся стандартом де факто.
Шифр RSA
Шифр RSA и ему подобные в своей основе имеет строгую математическую конструкцию – конечное числовое кольцо вычетов (КЧКВ) по модулю составного числа n = dмdб, где dм – меньший простой делитель, dб – больший делитель, оба очень большой разрядности до 300 десятичных цифр. Другим важным требованием к ключу шифра RSA является требование для разности делителей | dб – dм| = Δ, она должна иметь столь же высокую разрядность. Простой пример КЧКВ – это начальный фрагмент натурального ряда чисел с добавлением нулевого элемента. Кольцо образуют все числа подряд от 0 до n – 1. Более подробно о кольцах можно прочитать в учебниках по высшей алгебре.
Стойкость шифра RSA к раскрытию ключа оценивается как очень высокая и все усилия криптоаналитиков по взлому шифра (точнее его математического алгоритма) с момента его публикации (1978) успеха до сих пор не имели. Можно назвать ряд причин такого положения.
Публикуемые алгоритмы для реализации атак на шифр базируются в своей основе на концепции числового решета. С каждой новой публикацией мы видим несколько усовершенствованный алгоритм, но, по-видимому, эти усовершенствования недостаточны для достижения успеха. Идея решета Эратосфена была прогрессивной в его время, но сейчас это просто не срабатывает.
В интернете имеется список RSA-чисел. Конкурс, объявленный в 1991 году, с предложением их факторизовать пока далек от завершения. Анализ результатов мультипликативного разложения чисел из списка доступен, как и сами числа, открыт для всех. Из анализа следует, чем больше цифр в описании числа, тем большее время требовалось для его разложения. Напрашивается вывод о том, что для разложения модуля n используются алгоритмы весьма чувствительные к разрядности чисел, т.е. алгоритмы используют свойства чисел, сильно зависящие от их разрядности. С моей стороны предлагается использовать в алгоритмах атак свойства подобные «признакам делимости» чисел. Они практически от разрядности факторизуемого числа не зависят.
Публикуемые работы ограничиваются, как правило, обработкой непосредственно самого числа, игнорируя его окружение, свойства ближних и дальних соседей в рамках конкретной системы счисления. Очень большие надежды авторов и ожидания возлагаются на новые вычислительные средства: квантовые, фотонные, молекулярные и т. п. вычислители.
Авторы публикаций и владельцы алгоритмов шифрования не отрицают других новых подходов, и не исключают возможности создания новых алгоритмов на новых идеях, перед которыми задача факторизации больших чисел (ЗФБЧ) не устоит и ее решение будет успешным. Меня как автора настоящей публикации привлекают как раз новые оригинальные разработки в области решения ЗФБЧ. Большинство моих публикаций посвящены как раз новым подходам, начиная с синтеза моделей натурального ряда чисел (НРЧ), изучения их свойств и использования таких свойств при разработке новых оригинальных алгоритмов решения ЗФБЧ.*********
Об этом шифре написано достаточно много и вполне заслуженно. Это асимметричный блочный шифр замены известный с 1978 года, а преобразования, используемые в его алгоритме очень просты. В шифре используются модуль шифра n = pq (p и q простые числа одинаковой очень большой разрядности), n публикуется открыто, доступен всем, два ключа открытый е - открыто публикуется и доступен всем и d - закрытый ключ, он известен только получателю сообщений и сохраняемый в тайне. Устанавливает шифр, параметры шифра получатель сообщения и хранит в тайне значения p,q, d,φ(n). Здесь φ(n) - функция Эйлера, используемая для отыскания значения закрытого ключа d как результата решения сравнения ed = 1(modφ(n)). Решение сравнения находится путем применения расширенного алгоритма Евклида наибольшего общего делителя (НОД). Текстовое сообщение перед зашифрованием разбивается на блоки и оцифровывается. Значение блока mi не превышает модуля n > miшифра. Как видим, шифр устроен просто и доступен для понимания за короткое время. Надо еще сказать, что шифр реализуется над алгебраической структурой - конечным числовым кольцом вычетов по составному модулю Zn. Это означает, что все блоки исходного, шифрованного текстов, ключи е и d, простые числа p и q, значения функции Эйлера - это элементы означенного кольца. Все законы и кольцевые операции справедливы для элементов шифра
Зашифрование сообщения М = {m1,m2, ..., mk} из k блоков выполняется последовательно блок за блоком по формуле yi =mie(modn), где yi - блок шифртекста, mi- числовой блок исходного (открытого) текста, е - открытый ключ шифра, n - модуль шифра;
Расшифрование шифрсообщения Y= {y1,y2, ..., yk} из шифрованных блоков выполняется последовательно блок за блоком по формуле mi =yid(modn), где yi - блок шифртекста, mi- числовой блок исходного (открытого) текста, d- закрытый ключ шифра, n- модуль шифра;
Из известных шифров RSA можно считать долгожителем. В качестве однонаправленной функции fz(x) шифрования с потайным ходом (с лазейкой) в системе RSA используется дискретное возведение числового представления блока сообщения в степень ключа (открытого) шифрования Y =Me(modn).
Пример 2. Владелец «умного» устройства, подвергнувшегося атаке со стороны нарушителя, поставлен перед фактом – устройство перестало работать, его функционирование заблокировано. Если это замки на входных дверях, то ни войти, ни выйти из «умного» дома. На светящемся экране дисплея системы при проверке владелец видит последовательность чисел Y1 = 474 иY2 =407. Можно предположить, что это шифрованное сообщение нарушителя владельцу устройства.
Телефонным звонком по мобильному телефону нарушитель объявляет свои условия снятия блокировки. Это может быть банальное вымогательство денежной суммы. Нарушитель не лишен чувства юмора и дополнительно сообщает, что параметрами трех-буквенного шифра являются номер дома и возраст сына владельца. Что дает возможность владельцу самостоятельно разблокировать систему.
Если исходный текст будет восстановлен из шифртекста, то введение его в систему снимет ее блокировку. После проб и ошибок с 3-х буквенными шифрами владелец приходит к выводу о шифре RSA с модулем n = 527, равным номеру дома и открытым ключом е = 7 (число полных лет сына). Но даже в этих условия задача не из простых. Необходимо восстановить личный (закрытый) ключ нарушителя.
Для этого нужно знать значение функции Эйлера, а для ее вычисления делители составного модуля n. Делители находятся простым перебором, функцию Эйлера, зная делители, легко вычислить. Надо знать еще и расширенный алгоритм Евклида (НОД) нахождения обратных значений элементов кольца.
Владельцу раньше доводилось слышать о бесключевой атаке на шифр RSA. Для ее проведения достаточно знать открытый ключ е =7 и модуль n = 527 шифра. После звонка приятелю, компетентному в криптографии, принимается решение о самостоятельной разблокировке.
Формируется путем повторного многократного шифрования каждого блока на открытом ключе е последовательность числовых значений Yj, определяется такой j ≥ 1, для которого
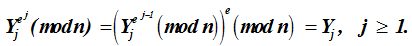
Из последнего соотношения видим, что на некотором шаге при возведении в степень е значения блока шифрованного текста
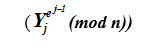
из шифрованных текстов Y1 = 474; Y2 = 407 получается всего за 3 возведения каждого шифрованного блока в степень открытого ключа е = 7 открытые тексты.
В примере 2 для Mj = M1 = 297 сформированы (((297)7(mod527))7(mod527))7(mod527) = 297 вычеты по модулю 527 за 3 шага.
Обрабатывается первый блок шифртекста Y1 = 474:
1-й шаг ((474)7(mod 527)= 537865465949405824 (mod 527) = 382;
2-й шаг ((382)7(mod 527)= 1186980379913527168 (mod 527) = 423;
3-й шаг ((423)7(mod 527)= 2423162679857794647 (mod 527) = 297;
4-й шаг, ШТ = ((297)7(mod 527)= 203842691587258713 (mod 527) = 474.
На этом шаге получили значение 474, с которого начали атаку.
Следовательно, на предыдущем шаге вычислений было получено значение открытого текста М1 = 297.
Теперь обрабатываем второй блок шифртекста Y2=407:
1-й шаг ((407)7(mod 527)= 1849953723041760743 (mod 527) = 16;
2-й шаг (( 16)7(mod 527)= 268435456 (mod 527) = 101;
3-й шаг ((101)7(mod 527)= 107213535210701 (mod 527) = 33;
4-й шаг, ШТ = ((33)7(mod 527)= 42618442977 (mod 527) = 407.
Получили значение 407, с которого начали возведение в степень открытого ключа, следовательно, на предыдущем шаге было получено значение открытого текста М2 = 33. Теперь обрабатываем оба блока открытого текста с целью возможности их прочтения. Переход к буквенному представлению не дает разгадки (смысла). Пробуем представить блоки в двоичном виде:
297 = 100101001 и 33 = 100001.
Запишем числа без пробелов 100101001100001, здесь 15 символов. Многие шифры имеют названия на английском языке используются латинские буквы. В английском языке 26 букв 5 символов на букву. Пробуем переход к десятичному представлению 100102 = 1810, 100112 = 1910, 000012 = 110 .

В нашем случае воспользуемся средней строкой чисел. получаем три буквы RSA - это название трехбуквенного шифра 100102 = R =1810, 100112 = S = 1910, 000012 = A = 110 . Можно полагать, что исходный текст расшифрован верно. Загрузка чисел в память устройства снимает его блокировку. В этот раз обошлось без выкупа, нарушитель дал шанс владельцу, которым тот успешно воспользовался.
Заключение
В статье рассмотрены шифры замены ( рамках простенького сценария) от самых простых до современного RSA. Бесключевая атака на RSA оказалась успешной только в силу неудачного выбора параметров системы шифрования.Здесь проявились законы кольца вычетов, которые пока не сформулированы, но проявляются на практике. За этим примером стоит, по-видимому, глубокая теория, которая еще требует своего создания и разработки. Об этом я уже раньше писал в 2014 году.
Замечание. Шифр RSA противостоит атакам более 40 лет. Но и он имеет слабые места. Так, например, текст из 6-и блоков: 001; 341;187;154; 373; 526 этим шифром с составным модулем n = 527 не может быть зашифрован ни на каком ключе.
Для каждого конкретного модуля существуют такие нешифруемые сообщения.
Литература
1.Алферов А.П. и др. Основы криптографии.- М.:Гелиос АРВ, 2001.- 480 с.
2. Маховенко Е.Б. Теоретико-числовые методы в криптографии. -М.: Гелиос АРВ, 2006. - 320 с.
3. Ростовцев А.Г. Алгебраические основы криптографии.- СПб.: Мир и семья, 2000. - 354 с.
4. Ростовцев А.Г., Маховенко Е.Б. Введение в криптографию с открытым ключом. -СПб.: Мир и семья, 2001. - 336 с.
5. Ростовцев А.Г., Маховенко Е.Б. Введение в теорию итерированных шифров.- СПб.:Мир и семья,2003. - 302 с.
6. Жельников В. Криптография от папируса до компьютера.- М.: АBF, 1996.-
7 . Уэзерелл Ч. Этюды для программистов. - М.: Мир, 1982. - 288 с.
8. Молдовян А.А. и др. Криптография: скоростные шифры. -СПб.: БХВ, 2002. - 496 с.


usbstor
А почему?
unsignedchar
1 в любой степени 1, наверное.
unsignedchar
Да, 526 mod 527 = -1, то же самое почти.
Pavgran
Потому что по модулю простых, на которые раскладывается модуль, эти числа имеют остатки (1,1); (1,0); (0,1); (1,-1); (-1,1); (-1,-1). При возведении в степень они не меняются (потому что экспонента нечётная).